Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
Хабр доступен 24/7 благодаря поддержке друзей
Комментарии 35
Выглядеть это будет примерно так: (λx.λy.x + y)x' y' = (λy.x' + y)y' = x' + y'.
а почему вы вводите терм "+" без его описания?
Потому что суть здесь не в терме "+", а в логике каррирования. Мне показалось, что это нагляднее, чем
f = λx.λy.s(f v) w((λy.[x → v]s) w)[y → w][x → v]sНу мне как человеку, спустя 12 лет окунувшимся в математическую логику снова и просто ради интереса, конечно непонятной будет ваша наглядная запись, а вот та, которую вы написали выше уже более понятна, но правда опять появляется новый терм →, и мне снова приходится спрашивать, что такое → здесь. Ну вы не отвечайте, для этого есть учебный материал. Просто когда сталкиваешься со сложными темами на хабре, всегда хочется прочитать про них не как они описаны в учебных материалах, а так как они связываются с реальными объектами в мире, чтобы было побольше живых примеров, с каким-нибудь, например кодом иллюстрирующим сложные лямда конструкции, если это возможно конечно. Ну в любом случае спасибо, тема хорошая, интересная и нужная!
опять появляется новый терм →
Это не терм, это операция подстановки, которая повляется при применении β-редукции к терму
f v w в такой вот обобщенной форме записи.P.S. по-моему, статья написана легким для восприятия языком; читать приятно.
а я пользовался понятием «терм» как сокращение для «терминал (терминальный символ)» используемое в формальной грамматике, ведь для лямбда исчисления можно тоже построить грамматику, таким образом в любом случае все специальные символы типа +, → и т.д., вводимые в грамматику лямбда исчисления, будут сначала терминальными символами, а потом они буду приобретать другие свойства и становиться термами в рамках уже формальной логики.
Можно пояснить, почему терм (λx.x x)(λx.x x) на каждом шаге будет порождать себя? Разве не верна цепочка вычислений (λx.x x)(λx.x x) -> (x) (λx.x x) -> (x) (x), которая не упрощается без дальнейшего понимания, что такое x?
Каррирование называется так по имени блюда «карри». Залить рис карри так, чтобы только часть его была покрыта карри, а часть оставалась белой.
Всю жизнь думал что в честь Хаскелла Карри (вики)
Извините, но всё же возьму на себя смелость утверждать, что лямбда-исчисление должен знать любой уважающий себя программист. Уважающий себя программист должен уметь работать с абстракциями, понимать классику обработки списков (Lisp) и regex'ы.
Вставьте больше примеров по каждой операции. Новичкам проще будет разобраться.
И таки да, классическую нотацию лучше не нарушать. Если кто-то в самом деле заинтересуется и полезет изучать материал подробнее (ведь это является целью статьи, я правильно понял?), долго будут разбираться, где творчество автора, а где общепринятая нотация… На этом этапе это совсем ненужная головоломка…
Вставьте больше примеров по каждой операции. Новичкам проще будет разобраться.
И таки да, классическую нотацию лучше не нарушать. Если кто-то в самом деле заинтересуется и полезет изучать материал подробнее (ведь это является целью статьи, я правильно понял?), долго будут разбираться, где творчество автора, а где общепринятая нотация… На этом этапе это совсем ненужная головоломка…
Извините, но всё же возьму на себя смелость утверждать, что вместо regex вы имели ввиду redex.
применение функции: x yА какая функция применяется? Я правильно понимаю, что и
x и y здесь — переменные?
Можете рассказать как работает Y-комбинатор?
Мне как-то непонятно, почему, зачем и как он принимает значение рекурсивно заданного типа.
Мне как-то непонятно, почему, зачем и как он принимает значение рекурсивно заданного типа.
Я могу.
Потому что это такой способ выражения рекурсивных анонимных функций. Если функция имеет собственное имя, то проблемы с рекурсивным определением не возникает: в таком случае самоприменение выражается через это самое имя. Например, банальный рекурсивный факториал:
Все эти if, =, −, ×, 0, 1 можно считать сокращениями (макросами), которые на самом деле раскрываются в нормальные комбинаторы (замкнутые абстракции):
Но вот F уже таким образом не раскроешь, так как она обращается к некоей переменной F, которая ни с чем не связывается ни одной лямбда-абстракцией внутри её определения. Если у нас есть глобальное окружение, которое магическим образом свяжет переменную F с функцией F внутри определения функции F, то проблемы с её рекурсивным определением не будет. Иначе остаётся только ухищрение в виде Y-комбинатора.
Суть ухищрения в явном использовании так называемых продолжений. Обычно считается, что функция возвращает своё значение в абстрактный «наверх» — тому, кто хочет получить вычисленное значение функции. Можно этот возврат значения сделать явным, передавая функции A другую функцию B, которую A вычислит, передав ей результат собственного вычисления в виде аргумента. Например, вычисление (+ 1 (+ 2 3)) можно представить в виде (+ 2 3 λx.(+ 1 x •)). Здесь функция + тернарная: принимает два слагаемых и продолжение, которому она передаёт результат сложения. Как видите, результат сложения 2 и 3 передаётся следующей функции под именем x, где к нему прибавляется 1, а результат сложения передаётся в некий •, что обозначает дальнейшие вычисления.
Такая форма записи (стиль передачи продолжений) явно показывает порядок вычислений и является функциональным аналогом SSA-формы, использующейся как представление императивных языков. Помимо всех остальных плюшек она позволяет очень легко записать рекурсию: ведь если функции передать в виде продолжения эту же функцию, то для рекурсии уже не надо никаких магических глобальных окружений — рекурсивная функция будет замкнутой и у неё будет локальная переменная, через которую она сможет сделать «самовызов».
Итак, задача сводится к тому, чтобы вызвать произвольную функцию f с одним аргументом — функцией-продолжением, которая вызывает f. (Остальные аргументы можно передать с помощью упомянутого каррирования.) Введём для этого специальный комбинатор Y.
Кульбит №1. Изящный способ удовлетворить предыдущее требование — это определить Y так, чтобы он возвращал то же, что передаёт в f. Тогда рекурсивный вызов (f n) можно записать в виде ((Y g) n), где g = λfn.• — рекурсивная функция f, в которой все рекурсивные вызовы делаются через локальную переменную f. Таким образом, должно выполняться равенство:
Однако, по этой формуле нельзя понять, как записать Y в виде лямбда-терма, не используя Y. Собственно, формула кристаллизует проблему, возникающую при рекурсивном вызове.
Окей, ссылаться на некий глобальный Y, чтобы получить такой же Y мы не можем. Но это ограничение можно обойти, передав нужную функцию как аргумент! Запишем Y по-другому, через функцию X, которой передадим такую же функцию X (которая не ссылается ни на X, ни на Y):
Кульбит №2. X надо записать в виде лямбда-терма:
причём в нём нельзя ссылаться на X или Y, можно использовать только свою переменную x или свободную переменную f. Аргументом X может быть некоторый другой терм Z, который равен X с точностью до альфа-конверсии (Z — такой же X, только его переменная x переименована в z). Вот именно этот хитрый момент и позволяет осуществить «рекурсивный вызов», применяя одную анонимную функцию к другой, но «такой же» анонимной функции — для этого надо считать вызов эквивалентной функции эквивалентным рекурсивному вызову функции.
Идём дальше, теперь немного очевидных наблюдений:
Синтезировав эти наблюдения, можно заметить, что
Кульбит №3. Cледим за руками. Предыдущее равенство подставляем в первое очевидное наблюдение:
и в то же время
то есть
Кульбит №4. Какой должна быть функция эта функция X
чтобы предыдущее свойство выполнялось? Достаточно заметить, что X используется таким образом, что переменная x внутри неё всегда связана с X (а вернее, с некоей функцией, которая ведёт себя так же, как X). Маленькое напряжение ума и желаемое определение становится очевидным:
Теперь подставляем X в Y и получаем определение Y-комбинатора из палаты мер и весов:
Как этим пользоваться. Возьмём факториал:
и дополним его её одним аргументом — функцией, которая вычисляет факториал.
Теперь F' не имеет рекурсии. Это обычный комбинатор (после раскрытия всяких if). Отлично, но что передать ему первым аргументом? От этой головной боли Y-комбинатор и избавляет:
Теперь F — это функция, которая принимает одно число, и рекурсивно вычисляет факториал. Проверим, выполняя редукцию в нормальном порядке (всё не раскрываю, так как запутаться можно же):
Потому что это такой способ выражения рекурсивных анонимных функций. Если функция имеет собственное имя, то проблемы с рекурсивным определением не возникает: в таком случае самоприменение выражается через это самое имя. Например, банальный рекурсивный факториал:
Все эти if, =, −, ×, 0, 1 можно считать сокращениями (макросами), которые на самом деле раскрываются в нормальные комбинаторы (замкнутые абстракции):
Но вот F уже таким образом не раскроешь, так как она обращается к некоей переменной F, которая ни с чем не связывается ни одной лямбда-абстракцией внутри её определения. Если у нас есть глобальное окружение, которое магическим образом свяжет переменную F с функцией F внутри определения функции F, то проблемы с её рекурсивным определением не будет. Иначе остаётся только ухищрение в виде Y-комбинатора.
Суть ухищрения в явном использовании так называемых продолжений. Обычно считается, что функция возвращает своё значение в абстрактный «наверх» — тому, кто хочет получить вычисленное значение функции. Можно этот возврат значения сделать явным, передавая функции A другую функцию B, которую A вычислит, передав ей результат собственного вычисления в виде аргумента. Например, вычисление (+ 1 (+ 2 3)) можно представить в виде (+ 2 3 λx.(+ 1 x •)). Здесь функция + тернарная: принимает два слагаемых и продолжение, которому она передаёт результат сложения. Как видите, результат сложения 2 и 3 передаётся следующей функции под именем x, где к нему прибавляется 1, а результат сложения передаётся в некий •, что обозначает дальнейшие вычисления.
Такая форма записи (стиль передачи продолжений) явно показывает порядок вычислений и является функциональным аналогом SSA-формы, использующейся как представление императивных языков. Помимо всех остальных плюшек она позволяет очень легко записать рекурсию: ведь если функции передать в виде продолжения эту же функцию, то для рекурсии уже не надо никаких магических глобальных окружений — рекурсивная функция будет замкнутой и у неё будет локальная переменная, через которую она сможет сделать «самовызов».
Итак, задача сводится к тому, чтобы вызвать произвольную функцию f с одним аргументом — функцией-продолжением, которая вызывает f. (Остальные аргументы можно передать с помощью упомянутого каррирования.) Введём для этого специальный комбинатор Y.
Кульбит №1. Изящный способ удовлетворить предыдущее требование — это определить Y так, чтобы он возвращал то же, что передаёт в f. Тогда рекурсивный вызов (f n) можно записать в виде ((Y g) n), где g = λfn.• — рекурсивная функция f, в которой все рекурсивные вызовы делаются через локальную переменную f. Таким образом, должно выполняться равенство:
Однако, по этой формуле нельзя понять, как записать Y в виде лямбда-терма, не используя Y. Собственно, формула кристаллизует проблему, возникающую при рекурсивном вызове.
Окей, ссылаться на некий глобальный Y, чтобы получить такой же Y мы не можем. Но это ограничение можно обойти, передав нужную функцию как аргумент! Запишем Y по-другому, через функцию X, которой передадим такую же функцию X (которая не ссылается ни на X, ни на Y):
Кульбит №2. X надо записать в виде лямбда-терма:
причём в нём нельзя ссылаться на X или Y, можно использовать только свою переменную x или свободную переменную f. Аргументом X может быть некоторый другой терм Z, который равен X с точностью до альфа-конверсии (Z — такой же X, только его переменная x переименована в z). Вот именно этот хитрый момент и позволяет осуществить «рекурсивный вызов», применяя одную анонимную функцию к другой, но «такой же» анонимной функции — для этого надо считать вызов эквивалентной функции эквивалентным рекурсивному вызову функции.
Идём дальше, теперь немного очевидных наблюдений:
Синтезировав эти наблюдения, можно заметить, что
Кульбит №3. Cледим за руками. Предыдущее равенство подставляем в первое очевидное наблюдение:
и в то же время
то есть
Кульбит №4. Какой должна быть функция эта функция X
чтобы предыдущее свойство выполнялось? Достаточно заметить, что X используется таким образом, что переменная x внутри неё всегда связана с X (а вернее, с некоей функцией, которая ведёт себя так же, как X). Маленькое напряжение ума и желаемое определение становится очевидным:
Теперь подставляем X в Y и получаем определение Y-комбинатора из палаты мер и весов:
Как этим пользоваться. Возьмём факториал:
и дополним его её одним аргументом — функцией, которая вычисляет факториал.
Теперь F' не имеет рекурсии. Это обычный комбинатор (после раскрытия всяких if). Отлично, но что передать ему первым аргументом? От этой головной боли Y-комбинатор и избавляет:
Теперь F — это функция, которая принимает одно число, и рекурсивно вычисляет факториал. Проверим, выполняя редукцию в нормальном порядке (всё не раскрываю, так как запутаться можно же):
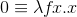
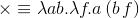
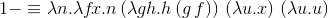
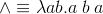
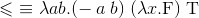
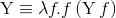
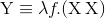
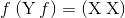
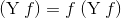
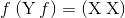
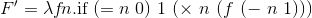
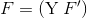
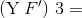
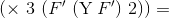
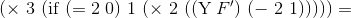
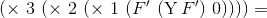
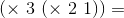
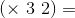
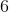
Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом.
Вообще-то за несколько лет до Тьюринга и Черча был Гедель со своими теоремами о неполноте.
Вы в данном случае не совсем правы. Проблема разрешимости (Чёрч и Тьюринг) и проблема полноты (Гёдель) — это совсем разные проблемы. Полнота формальной системы означает только сам факт того, что для любого утверждения из данной системы существует доказательство его истинности или ложности. А разрешимость — наличие алгоритма, способного такое доказательство построить.
Так, например, исчисление предикатов является полным, но не является разрешимым. Т.е. для любого утверждения есть доказательство его истинности или ложности, но принципиально не существует алгоритма, способного для любого утверждения это доказательство построить.
А можно вопрос в тему? Под логикой предикатов подразумевается логика первого порядка? Я не совсем понимаю, что это такое. Где граница между логикой первого парядка и логикой высшего порядка?
Правильно ли я понимаю, что в логике первого порядка есть фиксированное число предикатов и я могу их произвольно комбинировать с помощью кванторов и логических операций. Но в логике первого порядка нельзя сформулировать утверждение «для любого предиката P(x) верно ...»
Да, именно так. В логике второго порядка можно квантифицировать не только переменные, но и предикаты.
Вообще, в «обычной» математике логика второго порядка используется не очень часто, но иногда в ней возникает потребность. Например она используется при формулировке аксиомы математической индукции, которая выглядит примерно так: для любого предиката, если этот предикат истинен для 0, а также если из его истинности для
Вообще, в «обычной» математике логика второго порядка используется не очень часто, но иногда в ней возникает потребность. Например она используется при формулировке аксиомы математической индукции, которая выглядит примерно так: для любого предиката, если этот предикат истинен для 0, а также если из его истинности для
n следует его истинность для n+1, то тогда он истинен для любого числа. Полнота и существование алгоритма, который решает истинно утверждение или нет, это одно и то же.Это совершенно точно неверно. Об этом говорит, хотя бы, существование, с одной стороны, теоремы о полноте исчисления предикатов (Гёдель), и, с другой стороны, доказательство неразрешимости исчисления предикатов (Тьюринг и Чёрч).
Если для любого утверждения существует доказательство истинности или ложности, то элементарный переборный алгоритм его найдет.Честно говоря, точно не помню, в чем тут дело, но, по-моему, это объясняется тем, что исчисление предикатов содержит бесконечное число сигнатур.
Добавьте, пожалуйста, хаб Математика. Подписан на Математику, но Ваша статья обнаружена случайно.
Потерял нить на нескольких словах об области видимости... Прям сложно. И непонятно как гуглить разъяснения.
И никогда никто ни в одной статье/учебнике не объясняет что же означает клятая точка в этих всех ваших нотациях...
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
λ-исчисление. Часть первая: история и теория