Не помню, что меня так заело. Наверно, кто-нибудь обыграл меня в Балду с разгромным счетом (ее онлайн-вариант есть на Одноклассниках, Mail.ru и в куче других мест). Короче, я принял вызов. В прошлый раз так было с программкой для разгадки СУДОКУ. Но там все оказалось заметно проще.
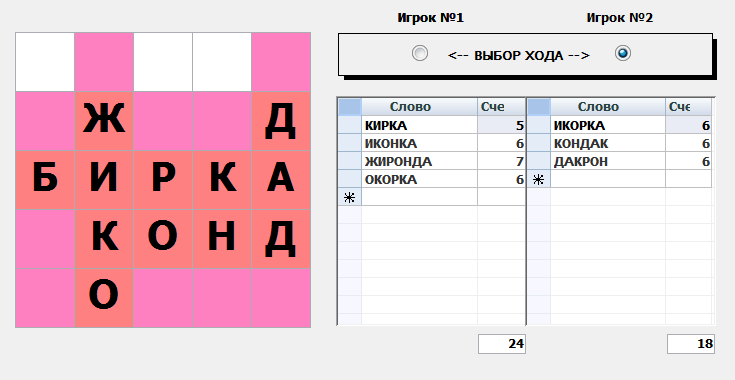
Балда, она же Волшебный Квадрат. Игроки добавляют на каждом шагу по одной букве, чтобы получилось осмысленное слово как можно большей длины.
Будучи программистом старой закалки (FORTRAN, PL1 и стопка перфокарт), я считаю, что решительно все равно, на чем писать код. Из кардинальных идей, случившихся в истории программирования, стоит упомянуть только объектную ориентированность и реляционную модель данных (ну и еще, пожалуй, функциональное программирование, всякие лямбда-вещи, в противоположность привычному, процедурному подходу). Главное, все же, Алгоритм! Которые все в основном изложены в семитомнике «Основы программирования» Дональда Кнута. А какие команды отрисуют вам окно, иконку и прочие прелести – дело десятое. Семитомник Кнута, как и базовая статья по реляционным базам Эдгара Кодда из Исследовательского центра IBM, появились во второй половине 60-х годов. То есть почти полвека тому. Вот почему я пишу на VBA и не отвлекаюсь ни на какие новомодные вещи.
Вызовов (вот не люблю эту кальку с английского challenge, а привык!) при написании игры, собственно, было два. Правильно прописать рекурсивный алгоритм, а затем оптимизировать поиск слов в словаре.
С самим алгоритмом все достаточно просто. Вот есть игровое поле 5 на 5 с уже вписанными буквами. Нужно добавить еще одну букву, примыкающую к существующим с какой-либо стороны (кроме как по диагонали), и просмотреть в словаре все возникающие варианты слов при всех возможных вариантах «обхода» игрового поля, заполненного буквами. Тут и возникает рекурсия.
Начинаем по порядку с любой буквы и идем в любую сторону, где есть еще одна буква. Так набирается слово для проверки. Сами буквы, уже включенные в проверяемое слово, должны быть исключены из дальнейших проверок, так как слово не может быть с пересечениями (2 раза использовать одну и ту же букву нельзя).
Набранную строку символов на каждом этапе ищем в словаре. Если слово найдено – запоминаем этот вариант, но продолжаем поиск, не прерывая рекурсии, так как может существовать и более длинное слово с тем же началом (обнаружив КОТ, не упускаем шанса найти также КОТОВАСИЯ, КОТОВОДСТВО и т.д.)
Сигналом для выхода из рекурсии (это, как мы помним, самая важная часть в написании рекурсивных функций) будет попросту отсутствие возможности выбрать еще одну букву, когда все возможные на данном шагу ходы исчерпаны (уже включены в проверяемое слово или находятся в недосягаемости от того места игрового поля, где мы оказались на данном шаге). Тогда мы делаем выход, то есть отступаем на шаг назад и пытаемся двинуться в другую сторону. Полный выход из рекурсии произ��йдет, когда мы переберем все возможные варианты – все маршруты обхода поля с буквами.
При этом только что добавленная буква должна попасть в слово, которое мы проверяем. Но это правило нельзя включить априори – может статься, что эта буква окажется вообще последней, так что эту проверку нужно провести только в самом конце, перед поиском в словаре.
В этом месте меня удивило количество возникающих вариантов. В разгар игры (когда игровое поле уже заполнено, но и свободных клеток остается достаточно), система просматривает более 100 000 (прописью – ста тысяч) вариантов слов на каждом шагу! Мы явно имеем дело с задачей экспоненциальной сложности от размера поля (NP-полнота?). Поэтому от изначальной идеи – просчитать всякую игру на много ходов вперед, чтобы выбрать тот вариант, который не даст противнику длинных слов в его черед (при условии, конечно, что мы пользуемся одним и тем же словарем!) пришлось отказаться.
Кстати, глубина рекурсии совсем невелика – как понятно из описанного алгоритма, она не превышает количества букв на поле в данный момент.
В качестве словаря я взял словарь Зализняка (это тот самый ученый-лингвист, чьи таблицы по морфологии русского языка, по образованию словоформ, были положены в основу проверки синтаксиса в Microsoft Word 6.0 Игорем Агамирзяном). Согласно правилам Балды, можно использовать только существительные в именительном падеже единственном числе, таковых в использованном мной словаре было ровно 43 304, от «АБАЖУРА» до «ЯЩУРА».
Итак, мы имеем сто тысяч вариантов слов (в пике – до 150 000), которые надо поискать в словаре из 43 304 слов. Это выходит более шести миллиардов просмотров словаря, если я не ошибаюсь в подсчетах. Первая версия программы задумывалась над каждым ходом по несколько минут, и это безобразие нельзя было, конечно, терпеть. Не говоря уже о том, что если использовать программу для борьбы с реальным соперником, то на обдумывание хода дается не более минуты. А хочется еще заглянуть хотя бы на шаг вперед, чтобы не подставить противнику какое-нибудь супердлинное слово в его ход.
Итак, оптимизация. Во-первых, вся работа должна осуществляться только в оперативной памяти, объем данных это вполне позволяет. Весь словарь считывается из таблицы в массив, по которому затем и осуществляется поиск. Но этого явно недостаточно.
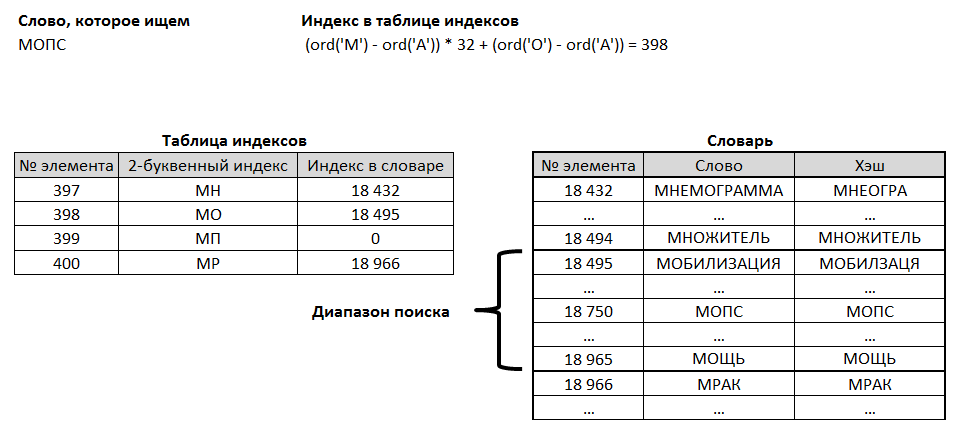
Вторым понятным способом оптимизировать является индексация. Её я сделал в 2-буквенном варианте. В отдельный массив, состоящий из всех возможных двухбуквенных пар, был внесен индекс, начиная с которого слова, начинающиеся на эти самые 2 буквы, расположены в массиве с полным словарем. Для того, чтобы не искать сначала в массиве индексов искомые 2 буквы, он был сделан полным, то есть содержал даже те пары букв, на которые в словаре нет ни одного слова. Таким образом, индекс в массиве индексов вычислялся напрямую из 2-х первых букв слова, которое мы ищем, то есть очень быстро.
Массив индексов также не занимает много места в памяти, его длина равна 32 x 32 = 1024 элемента. Реально, было несложно сделать индекс и 3-буквенным, но это, как показал опыт, не привело уже к дальнейшему ускорению.
Это еще не вся оптимизация! Я также расширил исходный словарь некоторым хэшем, если его можно так назвать – по сути, это было такое же слово, но в котором каждая буква встречалась только один раз (ПОТОП – ПТО). В результате самым быстрым вариантом поиска оказался такой:
— мы перебираем полный словарь, оставляя только те слова, которые содержат те же буквы, что и в слове, которое ищем;
— строим на этот урезанный словарь 2-буквенный индекс;
— ищем искомое слово, используя индекс.
Результат – поиск всех вариантов слов на каждом ходу занимает не более 2 секунд, при этом просматривается, как я уже говорил, до 150 000 слов в словаре и выдается до сотни вариантов хода — слов от 4-буквенных и выше. Можно также для каждого найденного варианта слова просчитать возможные будущие ходы противника – по цене 2 секунды за один вариант.
Теперь о MS Access. Я бесконечно влюблен в эту программу, так как она сочетает в себе вполне сносный реляционный движок базы данных, простое построение интерфейсов и мощный Visual Basic for Applications за сценой.
Последний, говорят, по скорости обработки строковой информации не уступает С++/ С# — что и было продемонстрировано оптимизацией нашей программы.
Что касается базы данных, то это, я считаю, единственно правильный формат хранения данных, на которых есть хоть какая-то структура. Это же позволяет писать программы «с накоплением» — то есть такие, расчет по которым занимает многие сутки (это всякие лингвистические задачи, которыми я порой балуюсь). Чтобы не потерять промежуточные результаты, их правильно скидывать в таблицы с некоторой регулярностью, которая не замедляет выполнение основных расчетов. Чтобы всегда была некоторая отправная точка, с которой можно было бы продолжить.
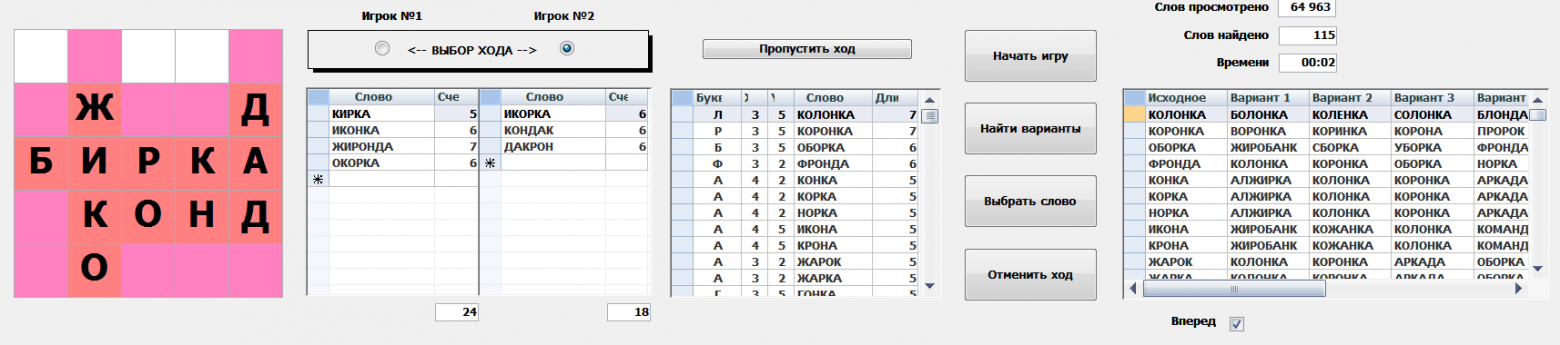
Интерфейс программы. Система предлагает все варианты ходов, отсортированные по убыванию длины. При желании, можно просмотреть вперед возможный следующий ход противника при выборе нами того или иного варианта слова.

А вот так выглядит матч с противником. Нужно аккуратно вносить его ходы, и программа подскажет самый лучший вариант.
Хотите меня поругать за нечестность? Но программу я написал и оптимизировал сам! Причем, играл на интерес, а не ради каких-нибудь благ. Более того, почти все соперники используют что-то подобное, но написанное не ими самими – это видно сразу. Откуда у 15-летнего парня, чей профиль полон фоток с котиками, знание слова ПРОЗЕЛИТИЗМ? («Что делает малютка Тиффани в неблагоприятном районе в час ночи с учебником квантовой физики в руках?»)

Балда, она же Волшебный Квадрат. Игроки добавляют на каждом шагу по одной букве, чтобы получилось осмысленное слово как можно большей длины.
Будучи программистом старой закалки (FORTRAN, PL1 и стопка перфокарт), я считаю, что решительно все равно, на чем писать код. Из кардинальных идей, случившихся в истории программирования, стоит упомянуть только объектную ориентированность и реляционную модель данных (ну и еще, пожалуй, функциональное программирование, всякие лямбда-вещи, в противоположность привычному, процедурному подходу). Главное, все же, Алгоритм! Которые все в основном изложены в семитомнике «Основы программирования» Дональда Кнута. А какие команды отрисуют вам окно, иконку и прочие прелести – дело десятое. Семитомник Кнута, как и базовая статья по реляционным базам Эдгара Кодда из Исследовательского центра IBM, появились во второй половине 60-х годов. То есть почти полвека тому. Вот почему я пишу на VBA и не отвлекаюсь ни на какие новомодные вещи.
Вызовов (вот не люблю эту кальку с английского challenge, а привык!) при написании игры, собственно, было два. Правильно прописать рекурсивный алгоритм, а затем оптимизировать поиск слов в словаре.
С самим алгоритмом все достаточно просто. Вот есть игровое поле 5 на 5 с уже вписанными буквами. Нужно добавить еще одну букву, примыкающую к существующим с какой-либо стороны (кроме как по диагонали), и просмотреть в словаре все возникающие варианты слов при всех возможных вариантах «обхода» игрового поля, заполненного буквами. Тут и возникает рекурсия.
Начинаем по порядку с любой буквы и идем в любую сторону, где есть еще одна буква. Так набирается слово для проверки. Сами буквы, уже включенные в проверяемое слово, должны быть исключены из дальнейших проверок, так как слово не может быть с пересечениями (2 раза использовать одну и ту же букву нельзя).
Набранную строку символов на каждом этапе ищем в словаре. Если слово найдено – запоминаем этот вариант, но продолжаем поиск, не прерывая рекурсии, так как может существовать и более длинное слово с тем же началом (обнаружив КОТ, не упускаем шанса найти также КОТОВАСИЯ, КОТОВОДСТВО и т.д.)
Сигналом для выхода из рекурсии (это, как мы помним, самая важная часть в написании рекурсивных функций) будет попросту отсутствие возможности выбрать еще одну букву, когда все возможные на данном шагу ходы исчерпаны (уже включены в проверяемое слово или находятся в недосягаемости от того места игрового поля, где мы оказались на данном шаге). Тогда мы делаем выход, то есть отступаем на шаг назад и пытаемся двинуться в другую сторону. Полный выход из рекурсии произ��йдет, когда мы переберем все возможные варианты – все маршруты обхода поля с буквами.
При этом только что добавленная буква должна попасть в слово, которое мы проверяем. Но это правило нельзя включить априори – может статься, что эта буква окажется вообще последней, так что эту проверку нужно провести только в самом конце, перед поиском в словаре.
В этом месте меня удивило количество возникающих вариантов. В разгар игры (когда игровое поле уже заполнено, но и свободных клеток остается достаточно), система просматривает более 100 000 (прописью – ста тысяч) вариантов слов на каждом шагу! Мы явно имеем дело с задачей экспоненциальной сложности от размера поля (NP-полнота?). Поэтому от изначальной идеи – просчитать всякую игру на много ходов вперед, чтобы выбрать тот вариант, который не даст противнику длинных слов в его черед (при условии, конечно, что мы пользуемся одним и тем же словарем!) пришлось отказаться.
Кстати, глубина рекурсии совсем невелика – как понятно из описанного алгоритма, она не превышает количества букв на поле в данный момент.
В качестве словаря я взял словарь Зализняка (это тот самый ученый-лингвист, чьи таблицы по морфологии русского языка, по образованию словоформ, были положены в основу проверки синтаксиса в Microsoft Word 6.0 Игорем Агамирзяном). Согласно правилам Балды, можно использовать только существительные в именительном падеже единственном числе, таковых в использованном мной словаре было ровно 43 304, от «АБАЖУРА» до «ЯЩУРА».
Итак, мы имеем сто тысяч вариантов слов (в пике – до 150 000), которые надо поискать в словаре из 43 304 слов. Это выходит более шести миллиардов просмотров словаря, если я не ошибаюсь в подсчетах. Первая версия программы задумывалась над каждым ходом по несколько минут, и это безобразие нельзя было, конечно, терпеть. Не говоря уже о том, что если использовать программу для борьбы с реальным соперником, то на обдумывание хода дается не более минуты. А хочется еще заглянуть хотя бы на шаг вперед, чтобы не подставить противнику какое-нибудь супердлинное слово в его ход.
Итак, оптимизация. Во-первых, вся работа должна осуществляться только в оперативной памяти, объем данных это вполне позволяет. Весь словарь считывается из таблицы в массив, по которому затем и осуществляется поиск. Но этого явно недостаточно.
Вторым понятным способом оптимизировать является индексация. Её я сделал в 2-буквенном варианте. В отдельный массив, состоящий из всех возможных двухбуквенных пар, был внесен индекс, начиная с которого слова, начинающиеся на эти самые 2 буквы, расположены в массиве с полным словарем. Для того, чтобы не искать сначала в массиве индексов искомые 2 буквы, он был сделан полным, то есть содержал даже те пары букв, на которые в словаре нет ни одного слова. Таким образом, индекс в массиве индексов вычислялся напрямую из 2-х первых букв слова, которое мы ищем, то есть очень быстро.
Массив индексов также не занимает много места в памяти, его длина равна 32 x 32 = 1024 элемента. Реально, было несложно сделать индекс и 3-буквенным, но это, как показал опыт, не привело уже к дальнейшему ускорению.
Это еще не вся оптимизация! Я также расширил исходный словарь некоторым хэшем, если его можно так назвать – по сути, это было такое же слово, но в котором каждая буква встречалась только один раз (ПОТОП – ПТО). В результате самым быстрым вариантом поиска оказался такой:
— мы перебираем полный словарь, оставляя только те слова, которые содержат те же буквы, что и в слове, которое ищем;
— строим на этот урезанный словарь 2-буквенный индекс;
— ищем искомое слово, используя индекс.

Результат – поиск всех вариантов слов на каждом ходу занимает не более 2 секунд, при этом просматривается, как я уже говорил, до 150 000 слов в словаре и выдается до сотни вариантов хода — слов от 4-буквенных и выше. Можно также для каждого найденного варианта слова просчитать возможные будущие ходы противника – по цене 2 секунды за один вариант.
Теперь о MS Access. Я бесконечно влюблен в эту программу, так как она сочетает в себе вполне сносный реляционный движок базы данных, простое построение интерфейсов и мощный Visual Basic for Applications за сценой.
Последний, говорят, по скорости обработки строковой информации не уступает С++/ С# — что и было продемонстрировано оптимизацией нашей программы.
Что касается базы данных, то это, я считаю, единственно правильный формат хранения данных, на которых есть хоть какая-то структура. Это же позволяет писать программы «с накоплением» — то есть такие, расчет по которым занимает многие сутки (это всякие лингвистические задачи, которыми я порой балуюсь). Чтобы не потерять промежуточные результаты, их правильно скидывать в таблицы с некоторой регулярностью, которая не замедляет выполнение основных расчетов. Чтобы всегда была некоторая отправная точка, с которой можно было бы продолжить.

Интерфейс программы. Система предлагает все варианты ходов, отсортированные по убыванию длины. При желании, можно просмотреть вперед возможный следующий ход противника при выборе нами того или иного варианта слова.
А вот так выглядит матч с противником. Нужно аккуратно вносить его ходы, и программа подскажет самый лучший вариант.
Хотите меня поругать за нечестность? Но программу я написал и оптимизировал сам! Причем, играл на интерес, а не ради каких-нибудь благ. Более того, почти все соперники используют что-то подобное, но написанное не ими самими – это видно сразу. Откуда у 15-летнего парня, чей профиль полон фоток с котиками, знание слова ПРОЗЕЛИТИЗМ? («Что делает малютка Тиффани в неблагоприятном районе в час ночи с учебником квантовой физики в руках?»)
