Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
Шикарная статья, но у меня вопрос, вот там у вас "схема вводимых приближений" и от релятивизма и прочих радостей, сразу отказываются. А поправки от них вниз по схеме распространяются? или уравнение Дирака с прочими радостями, не существенно влияют на получаемые дальше модели (понятно что все зависит от той системы для которой модель и строится, но все таки)?
С частотой радио- и микроволн (и даже длинноволнового инфракрасного излучения, ИК=IR) вращаются разные молекулы в газовой фазе
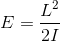 , где L — момент импульса, а I — момент инерции. В выражении же через угловую скорость она записывается как
, где L — момент импульса, а I — момент инерции. В выражении же через угловую скорость она записывается как 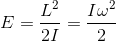 ,
,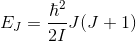 ,
, 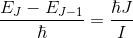
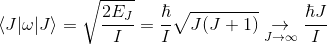 .
.Откуда дровишки про то, что таутомерия «завязана» на тоннельный эффект?
Это, кхм, крайне необщепринятое мнение.
В отличие от множества примеров доказанных межмолекулярных механизмов.
И вроде бы тоже можно численно чтото симулировать.
Вопрос — откуда столько специфичных терминов в вашей классификации моделей?
А если численно, уравнения Шрёдингера достаточно?
Еще вопрос — а для квант мех есть чтото наподобие физ движков вроде Bullet?
Мне понять хочется откуда сложность.
Но вот этот момент непонятен — что мне мешает решать задачу как ур. в частных производных и искать эту функцию как тепловое или эл магн поле? В тех же полях нет этого комбинаторного взрыва переходов, откуда они при решении ур Шредингера?
уравнение Шрёдингера — это уравнение теплопроводности с комплексным коэффициентом теплопроводности.
Насколько часто Вам нужно решать уравнения Максвелла или уравнение теплопроводности, скажем, в 30-ти мерном пространстве
Дело ведь не в комплексности. или не понял ваш ответ.
Значит вы полагаете дело только в размерности задачи?
Но размерность я могу и в классивеской механике создать,
или в той же электродинамике.
Размерность ведь параметрическая.
А про то откуда в принципе возникают вероятности переходов, матрица этих вероятностей
Т.е. в основе нормальное уравнение, 2го порядка, в частных производных. Но проблемы почему то совершенно другие чем в электродинамике или механике.
Значит вы полагаете дело только в размерности задачи? Но размерность я могу и в классивеской механике создать, или в той же электродинамике.
Вопрос — откуда столько специфичных терминов в вашей классификации моделей?Из-за практической сложности симуляции на компьютере. Даже, к примеру, модель воды симулировать сложно. Одна молекула воды для уравнения Шрёдингера — непосильная задача, поэтому вы делаете каскад приближений. Каждое такое приближение — отдельный термин в модели. В результате получается классификация моделей воды, каждая — со своей областью применимости, с сильными и слабыми сторонами.
Они возникают из желания построить аналитическую модель?Да, из желания построить достаточно простую модель, которую можно запихнуть в компьютер.
А если численно, уравнения Шрёдингера достаточно?Нет. В примере с водой уравнение Шрёдингера вообще стараются не использовать. Это невообразимо сложно для компьютера. Вообще, было бы довольно глупо, если бы сложные квантовые модели симулировались с помощью заведомо более простых классических компьютеров без каких-либо приближений, не так ли?
Но есть хорошая штука — адиабатическое приближение. Точно смысла не помнюНу, вы его в принципе описали. Идея в том, что раз электроны и ядра «живут» на совершенно разных временных масштабах, можно считать, что ядра живут в поле, усредненном по всем положениям электронов, а электроны живут в поле неподвижных ядер.
После этого мы замечаем, что электроны у нас почти в 2000 раз легче ядер, поэтому под действием кулоновского притяжения к ядрам и кулоновского отталкивания друг от друга, они движутся куда быстрее ядер. В итоге электронам кажется, что ядра заморожены. Поэтому электрончики спокойно принимают наивыгоднейшую для себя конфигурацию, и стоит ядрам чуть-чуть подвинуться, так электроны уже перестроились, как им удобнее. Ядра же видят только некоторый усреднённый потенциал, создаваемый электронами и кулоновскими взаимодействиями всего со всем, а сами детали движения электронов не видят. Это разделение электронов и ядер носит название «приближение Борна-Оппенгеймера» (да, это тот самый Роберт Оппенгеймер, он не только бомбой известен).
Какова средняя скорость движения жаб в зависимости от N, p?«методом Монте-Карло»: запускаем жаб для заданных N и p, считаем количество жаб, пересекших пруд и после 100500го раза смотрим на среднее, не?
Причем в квантовой химии часть жаб скачет спиной вверх, а часть спиной вниз при этом функция распределения должна быть строго антисимметрична относительно перестановки «двух разных спин»
вплоть до области γ-квантов
А что говорят об этом квантово-химические расчеты?
ab initio квантово-химические расчеты на классических компьютерах ограничиваются простыми или модельными задачами в ожидании появления квантовых процессоров?
Один из авторов статьи, кстати, Kieron Burke — придумал в свое время (с друзьями), на мой взгляд, лучший DFT функционал всех времен и народов — на деле доказал, что «умел думать головой».
Просто всё равно все DFT методы масштабируются как O(M4)-O(M5) в зависимости от размера базиса (M),DFT — в подавляющем большинстве O(M3), инфа 100%. O(M5) — я вообще не в курсе о таких дорогих методах в DFT. Это сложность MP2 (т.е. не самого MP2, а поворота кулоновских интегралов).
DFT — в подавляющем большинстве O(M3), инфа 100%.
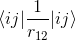
O(M5) — я вообще не в курсе о таких дорогих методах в DFT. Это сложность MP2 (т.е. не самого MP2, а поворота кулоновских интегралов).
With an expansion of the orbitals in basis functions, the number of integrals necessary for solving the KS equations rises as Mbasis4, owing to the Coulomb integrals in the J functional (and possibly also “exact” exchange in the hybrid methods). The number of grid points for the numerical Exc integration (eq. (6.61)) increases linearly with the system size, and the computational effort for the exchange–correlation term rises as GM2 basis, i.e. a cubic dependence of the system size. When the Coulomb (and possibly “exact” exchange) term is evaluated directly from integrals over basis functions, DFT methods scale formally as Mbasis4.
Nevertheless, the formal Mbasis4 scaling has spawned approaches that reduce the dependence to Mbasis3. This may be achieved by fitting the electron density to a linear combination of functions, and using the fitted density in evaluating the J integrals in the Coulomb term.
Кулоновское отталкивание <ij|ij> считается за O(M2). Это обменное взаимодействие <ij|ji> считается за O(M4).
В рельности же легче перейти в координатный или импульсный базис и посчитать там кулоновское отталкивание.
 образуют непрерывный спектр, нормированный на δ-функцию. Поэтому реализации подобной схемы для газофазных расчётов (подобно GPW технике в CP2K) требуют всё тех же дополнительных предположений и параметров (выбора ячейки достаточно большого размера, чтобы избежать self interaction и cutoff-а по энергии, хотя последнее — это естественная штука). Из-за этого подобный подход в случае молекул в вакууме проще
образуют непрерывный спектр, нормированный на δ-функцию. Поэтому реализации подобной схемы для газофазных расчётов (подобно GPW технике в CP2K) требуют всё тех же дополнительных предположений и параметров (выбора ячейки достаточно большого размера, чтобы избежать self interaction и cutoff-а по энергии, хотя последнее — это естественная штука). Из-за этого подобный подход в случае молекул в вакууме прощеназвать «технической приблудой»
они концептуально проще, нежели атомные базисы со всеми их хвостами и перекрытиями.
 ). Поэтому, насколько я знаю, выигрыш в масштабировании от подобного перехода к плосковолновым базисам компенсируется увеличением размеров этих базисов. Но тут я могу и ошибаться, поскольку с плосковолновыми расчётами особо не контактировал.
). Поэтому, насколько я знаю, выигрыш в масштабировании от подобного перехода к плосковолновым базисам компенсируется увеличением размеров этих базисов. Но тут я могу и ошибаться, поскольку с плосковолновыми расчётами особо не контактировал.А подробнее можете сказать какие данные в CSD и что нужно для получения базы/доступа?
Требуется ли «институтская почта»?
Поскольку она предполагает допуск к ICSD, не уверен.
Вот ссылка на заведомо бесплатный поиск:
More advanced search functionality and additional curated data for the Cambridge Structural Database (CSD) and the Inorganic Crystal Structure Database (ICSD) is available through the CSD-System and ICSD, respectively. Click here for more information.
может у CSD она нормальная.
Скорость, точность, устойчивость рассчетов, и тп… Интересно же, для нас это просто строчки кода :)
Simulation theory: взаимосвязь квантово-химических расчётов и Реальности