Нейросети и глубокое обучение, глава 5: почему глубокие нейросети так сложно обучать?

Содержание

• Глава 1: использование нейросетей для распознавания рукописных цифр
• Глава 2: как работает алгоритм обратного распространения
• Глава 3:
  • ч.1: улучшение способа обучения нейросетей
    
  • ч.2: почему регуляризация помогает уменьшать переобучение?
    
  • ч.3: как выбрать гиперпараметры нейросети?
    
• Глава 4: визуальное доказательство того, что нейросети способны вычислить любую функцию
• Глава 5: почему глубокие нейросети так сложно обучать?
• Глава 6:
  • ч.1: глубокое обучение
  • ч.2: недавний прогресс в распознавании изображений
• Послесловие: существует ли простой алгоритм для создания интеллекта?

Представьте, что вы – инженер, и вас попросили разработать компьютер с нуля. Как-то раз вы сидите в офисе, изо всех сил проектируете логические контуры, распределяете вентили AND, OR, и так далее,- и вдруг входит ваш босс и сообщает вам плохие новости. Клиент только что решил добавить неожиданное требование к проекту: схема работы всего компьютера должна иметь не более двух слоёв:



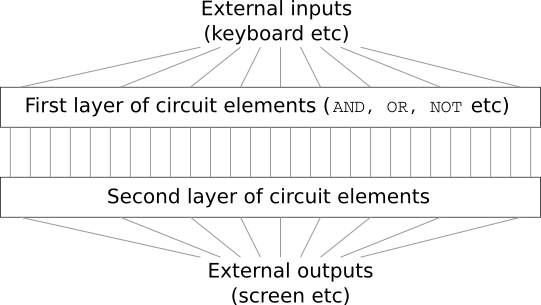
Вы поражены, и говорите боссу: «Да клиент спятил!»

Босс отвечает: «Я тоже так думаю. Но клиент должен получить то, что хочет».

На самом деле в некоем узком смысле клиент не совсем безумен. Допустим, вам позволят использовать особый логический вентиль, позволяющий вам связать через AND любое количество входов. А ещё вам разрешено использовать вентиль NAND с любым количеством входов, то есть, такой вентиль, который складывает множество входов через AND, а потом обращает результат в противоположный. Оказывается, что с такими особыми вентилями можно вычислить любую функцию при помощи всего лишь двухслойной схемы.

Однако только потому, что что-то можно сделать, не значит, что это стоит делать. На практике при решении задач, связанных с проектированием логических схем (и почти всех алгоритмических задач) мы обычно начинаем с того, что решаем подзадачи, а потом постепенно собираем полное решение. Иначе говоря, мы строим решение посредством множества уровней абстракции.

К примеру, допустим, мы проектируем логическую схему для перемножения двух чисел. Вполне вероятно, что мы захотим построить её из подсхем, реализующих такие операции, как сложение двух чисел. Подсхемы сложения, в свою очередь, будут состоять из подподсхем, складывающих два бита. Грубо говоря, наша схема будет выглядеть так:



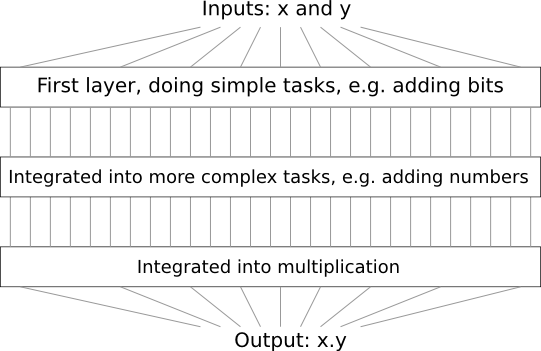
То есть, последняя схема содержит не менее трёх слоёв элементов схемы. На самом деле, в ней, вероятно, будет больше трёх слоёв, когда мы будем разбивать подзадачи на более мелкие, чем те, что я описал. Но принцип вы поняли.

Поэтому глубокие схемы облегчают процесс проектирования. Но они помогают не только в проектировании. Есть математические доказательства того, что для вычисления некоторых функций в очень неглубоких схемах требуется использовать экспоненциально большее количество элементов, чем в глубоких. К примеру, есть знаменитая серия научных работ 1980-х годов, где показано, что вычисление чётности набора битов требует экспоненциально большего количества вентилей с неглубокой схемой. С другой стороны, при использовании глубоких схем легче вычислять чётность при помощи небольшой схемы: вы просто вычисляете чётность пар битов, а потом используете результат для подсчёта чётности пар пар битов, и так далее, быстро приходя к общей чётности. Поэтому глубокие схемы могут быть гораздо более мощными, чем неглубокие.

Пока что в этой книге использовался подход к нейросетям (НС), похожий на запросы безумного клиента. Почти у всех сетей, с которыми мы работали, был единственный скрытый слой нейронов (плюс входной и выходной слои):



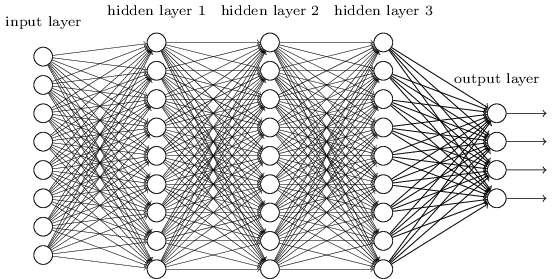
Эти простые сети оказались весьма полезными: в предыдущих главах мы использовали такие сети для классификации рукописных чисел с точностью, превышающей 98%! Тем не менее, интуитивно понятно, что сети с большим количеством скрытых слоёв будут гораздо более мощными:



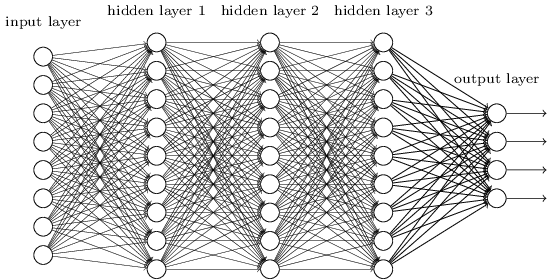
Такие сети могут использовать промежуточные слои для создания множества уровней абстракции, как в случае с нашими булевскими схемами. К примеру, в случае распознавания образов, нейроны первого слоя могут научиться распознавать грани, нейроны второго слоя – более сложные формы, допустим, треугольники или прямоугольники, созданные из граней. Затем третий слой сможет распознавать ещё более сложные формы. И так далее. Вероятно, эти многие слои абстракции дадут глубоким сетям убедительное преимущество в решении задач по распознаванию сложных закономерностей. Более того, как и в случае со схемами, существуют теоретические результаты, подтверждающие, что глубокие сети по сути своей имеют больше возможностей, чем неглубокие.

Как нам обучать подобные глубокие нейросети (ГНС)? В данной главе мы попробуем обучить ГНС используя нашу рабочую лошадку среди обучающих алгоритмов – стохастический градиентный спуск с обратным распространением. Однако мы столкнёмся с проблемой – наши ГНС не будут работать сильно лучше (если вообще превзойдут), чем неглубокие.

Эта неудача кажется странной в свете дискуссии, приведённой выше. Но вместо того, чтобы махнуть на ГНС рукой, мы углубимся в проблему и попытаемся понять, почему ГНС тяжело обучать. Когда мы поближе познакомимся с вопросом, мы обнаружим, что разные слои в ГНС обучаются с крайне разными скоростями. В частности, когда последние слои сети обучаются хорошо, первые часто застревают во время обучения, и почти ничему не обучаются. И дело не в простом невезении. Мы обнаружим фундаментальные причины для замедления обучения, которые связаны с использованием техник обучения на основе градиента.

Зарывшись в эту проблему поглубже, мы узнаем, что может происходит и обратное явление: ранние слои могут обучаться хорошо, а более поздние — застревать. На самом деле, мы обнаружим внутреннюю нестабильность, связанную с обучением градиентным спуском в глубоких многослойных НС. И из-за этой нестабильности либо ранние, либо поздние слои часто застревают при обучении.

Всё это звучит довольно неприятно. Но погрузившись в эти трудности, мы можем начать разрабатывать идеи о том, что нужно сделать для эффективного обучения ГНС. Поэтому эти исследования станут хорошей подготовкой к следующей главе, где мы будем использовать глубокое обучение для подхода к задачам распознавания изображений.

Проблема исчезающего градиента

Так что же идёт не так, когда мы пытаемся обучить глубокую сеть?

Чтобы ответить на этот вопрос, вернёмся к сети, содержащей всего один скрытый слой. Как обычно, мы будем использовать задачу классификации цифр MNIST в качестве песочницы для обучения и экспериментов.

Если хотите повторять все эти действия на компьютере, у вас должны быть установлены Python 2.7, библиотека Numpy, и копия кода, которую можно взять с репозитория:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

Можно обойтись и без git, просто скачав данные и код. Перейдите в подкаталог src и из оболочки python загрузите данные MNIST:

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()

Настраиваем сеть:

>>> import network2
>>> net = network2.Network([784, 30, 10])

У такой сети есть 784 нейрона во входном слое, соответствующие 28×28=784 пикселям входного изображения. Мы используем 30 скрытых нейронов и 10 выходных, соответствующих десяти возможным вариантам классификации цифр MNIST ('0', '1', '2', …, '9').

Попробуем обучать нашу сеть в течение 30 целых эпох с использованием мини-пакетов из 10 обучающих примеров за раз, скорость обучения η=0,1 и параметр регуляризации λ=5,0. Во время обучения мы будем отслеживать точность классификации через validation_data:

>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, 
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)

Мы получим точность классификации в 96,48% (или около того – при разных запусках цифры будут варьироваться), сравнимую с нашими ранними результатами с похожими настройками.

Давайте добавим ещё один скрытый слой, также содержащий 30 нейронов, и попытаемся обучить сеть с теми же гиперпараметрами:

>>> net = network2.Network([784, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, 
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)

Точность классификации улучшается до 96,90%. Это вдохновляет – небольшое увеличение глубины помогает. Давайте добавим ещё один скрытый слой из 30 нейронов:

>>> net = network2.Network([784, 30, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, 
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)

Это никак не помогло. Результат даже упал до 96,57%, значения, близкого к первоначальной неглубокой сети. А если мы добавим ещё один скрытый слой:

>>> net = network2.Network([784, 30, 30, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, 
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)

Тогда точность классификации опять упадёт, уже до 96,53%. Статистически это падение, вероятно, незначительно, однако и ничего хорошего в этом нет.

Такое поведение кажется странным. Интуитивно кажется, что дополнительные скрытые слои должны помочь сети обучиться более сложным функциям классификации, и лучше справиться с задачей. Уж конечно результат не должен ухудшаться, ведь в худшем случае дополнительные слои просто не будут ничего делать. Однако этого не происходит.

Так что же происходит? Давайте предположим, что дополнительные скрытые слои могут помочь в принципе, и что проблема в том, что наш обучающий алгоритм не находит правильных значений для весов и смещений. Нам хотелось бы понять, что не так с нашим алгоритмом, и как его улучшить.

Чтобы понять, что пошло не так, давайте визуализируем процесс обучения сети. Ниже я построил часть сети [784,30,30,10], в которой есть два скрытых слоя, в каждом из которых по 30 скрытых нейронов. На диаграмме у каждого нейрона есть полоска, обозначающая скорость изменения в процессе обучения сети. Большая полоска значит, что веса и смещения нейрона меняются быстро, а маленькая – что они меняются медленно. Точнее, полоска обозначает градиент ∂C/∂b нейрона, то есть, скорость изменения стоимости по отношению к смещению. В главе 2 мы увидели, что эта величина градиента контролирует не только скорость изменения смещения в процессе обучения, но и скорость изменения входных весов нейрона. Не волнуйтесь, если вы не можете вспомнить эти детали: надо просто иметь в виду, что эти полоски обозначают, насколько быстро меняются веса и смещения нейронов в процессе обучения сети.

Для упрощения диаграммы я нарисовал только шесть верхних нейронов в двух скрытых слоях. Я опустил входящие нейроны, поскольку у них нет весов или смещений. Я опустил и выходные нейроны, поскольку мы сравниваем два слоя, и имеет смысл сравнивать слои с одинаковым количеством нейронов. Диаграмма построена при помощи программы generate_gradient.py в самом начале обучения, то есть, сразу после того, как сеть была инициализирована.



Сеть была инициализирована случайно, поэтому такое разнообразие в скорости обучения нейронов неудивительно. Однако сразу же бросается в глаза, что во втором скрытом слое полоски в основном гораздо больше, чем в первом. В итоге нейроны во втором слое будут учиться гораздо быстрее, чем в первом. Совпадение ли это, или нейроны во втором слое, вероятно, в общем будут обучаться быстрее нейронов в первом?

Чтобы узнать точно, хорошо будет иметь общий способ сравнения скорости обучения в первом и втором скрытых слоях. Для этого давайте обозначим градиент как δ^l_j = ∂C/∂b^l_j, то есть, как градиент нейрона №j в слое №l. Во второй главе мы называли это «ошибкой», но здесь я будут неформально называть это «градиентом». Неформально – поскольку в эту величину не входят явно частные производные стоимости по весам, ∂C/∂w. Градиент δ¹ можно представлять себе как вектор, чьи элементы определяют, насколько быстро обучается первый скрытый слой, а δ² — как вектор, чьи элементы определяют, насколько быстро обучается второй скрытый слой. Длины этих векторов мы используем, как приблизительные оценки скорости обучения слоёв. То есть, к примеру, длина || δ¹ || измеряет скорость обучения первого скрытого слоя, а длина || δ² || измеряет скорость обучения второго скрытого слоя.

С такими определениями и с той же конфигурацией, что указана выше, мы обнаружим, что || δ¹ || = 0,07, а || δ² || = 0,31. Это подтверждает наши подозрения: нейроны во втором скрытом слое обучаются гораздо быстрее, чем нейроны в первом скрытом слое.

Что будет, если мы добавим больше скрытых слоёв? С тремя скрытыми слоями в сети [784,30,30,30,10] соответствующие скорости обучения составят 0,012, 0,060 и 0,283. Опять первые скрытые слои обучаются гораздо медленнее последних. Добавим ещё один скрытый слой с 30 нейронами. В данном случае соответствующие скорости обучения составят 0,003, 0,017, 0,070 и 0,285. Закономерность сохраняется: ранние слои обучаются медленнее поздних.

Мы изучали скорость обучения в самом начале – сразу после инициализации сети. Как же меняется эта скорость по мере обучения? Давайте вернёмся и посмотрим на сеть с двумя скрытыми слоями. Скорость обучения меняется в ней так:



Для получения этих результатов я использовал пакетный градиентный спуск с 1000 обучающих изображений и обучение в течение 500 эпох. Это немного отличается от наших обычных процедур – я не использовал мини-пакеты и взял всего 1000 обучающих изображений, вместо полного набора из 50 000 штук. Я не пытаюсь хитрить и обманывать вас, но оказывается, что использование стохастического градиентного спуска с мини-пакетами привносит в результаты гораздо больше шума (но если усреднять шум, то результаты получаются похожими). Используя выбранные мною параметры легко сгладить результаты, чтобы мы могли увидеть, что происходит.

В любом случае, как видим, два слоя начинают обучение с двух очень разных скоростей (что нам уже известно). Затем скорость обоих слоёв очень быстро падает, после чего происходит отскок. Однако всё это время первый скрытый слой обучается гораздо медленнее второго.

Что насчёт более сложных сетей? Вот результаты похожего эксперимента, но уже с сетью с тремя скрытыми слоями [784,30,30,30,10]:



И снова первые скрытые слои обучаются гораздо медленнее последних. Наконец, попробуем добавить четвёртый скрытый слой (сеть [784,30,30,30,30,10]), и посмотрим, что произойдёт при её обучении:



И снова первые скрытые слои обучаются гораздо медленнее последних. В данном случае первый скрытый слой обучается примерно в 100 раз медленнее последнего. Неудивительно, что у нас были такие проблемы с обучением этих сетей!

Мы провели важное наблюдение: по крайней мере, в некоторых ГНС градиент уменьшается при движении в обратную сторону по скрытым слоям. То есть, нейроны в первых слоях обучаются гораздо медленнее нейронов в последних. И хотя мы наблюдали этот эффект всего в одной сети, существуют фундаментальные причины того, почему это происходит во многих НС. Это явление известно под названием «проблемы исчезающего градиента» (см. работы 1, 2).

Почему возникает проблема исчезающего градиента? Есть ли способы её избежать? Как нам быть с ней при обучении ГНС? На самом деле вскоре мы узнаем, что она не является неизбежной, хотя альтернатива ей и не выглядит очень уж привлекательное: иногда в первых слоях градиент оказывается гораздо больше! Это уже проблема взрывного роста градиента, и в ней не больше хорошего, чем в проблеме исчезающего градиента. В целом оказывается, что градиент в ГНС нестабилен, и склонен либо к взрывному росту, либо к исчезновению в первых слоях. Эта нестабильность является фундаментальной проблемой для градиентного обучения ГНС. Это то, что нам нужно понять, и по возможности как-то решить.

Одна из реакций на исчезающий (или нестабильный) градиент – подумать, а является ли это на самом деле серьёзной проблемой? Ненадолго отвлечёмся от НС, и представим, что мы пытаемся численным образом минимизировать функцию f(x) от одного переменного. Разве не было бы здорово, если бы производная f′(x) была малой? Не означало бы это, что мы уже близки к экстремуму? И точно так же, не означает ли небольшой градиент в первых слоях ГНС, что нам уже не нужно сильно подстраивать веса и смещения?

Конечно же, нет. Вспомним, что мы случайным образом инициализировали веса и смещения сети. Крайне маловероятно, что наши изначальные веса и смешения хорошо справятся с тем, чего мы хотим от нашей сети. В качестве конкретного примера рассмотрим первый слой весов в сети [784,30,30,30,10], классифицирующей цифры MNIST. Случайная инициализация означает, что первый слой выбрасывает большую часть информации о входящем изображении. Даже если бы более поздние слои были тщательно обучены, им бы было чрезвычайно сложно определять входящее сообщение, просто из-за недостатка информации. Поэтому совершенно невозможно представить, что первому слою просто не нужно обучаться. Если мы собираемся обучать ГНС, нам надо понять, как решать проблему исчезающего градиента.

Что вызывает проблему исчезающего градиента? Нестабильные градиенты в ГНС

Чтобы понять, как появляется проблема исчезающего градиента, рассмотрим простейшую НС: всего с одним нейроном в каждом слое. Вот сеть с тремя скрытыми слоями:



Здесь w₁, w₂,… – это веса, b₁, b₂,… – смещения, С – некая функция стоимости. Просто для напоминания скажу, что выход a_j с нейрона №j равен σ(z_j), где σ — обычная сигмоидная функция активации, а z_j = w_ja_j−1+b_j — взвешенный вход нейрона. Функцию стоимости я изобразил в конце, чтобы подчеркнуть, что стоимость является функцией от выхода сети, a₄: если реальный выход близок к желаемому, тогда стоимость будет маленькой, а если далёк – то большой.

Изучим градиент ∂C/∂b₁, связанный с первым скрытым нейроном. Найдём выражение для ∂C/∂b₁ и, изучив его, поймём, почему возникает проблема исчезающего градиента.

Начнём с демонстрации выражения для ∂C/∂b₁. Выглядит неприступно, но на самом деле структура его проста, и я скоро опишу её. Вот это выражение (пока игнорируйте саму сеть и отметьте, что σ′ — просто производная от функции σ):



Структура выражения такова: для каждого нейрона в сети имеется член умножения σ′(z_j), для каждого веса имеется w_j, и ещё есть последний член, ∂C/∂a₄, соответствующий функции стоимости. Заметьте, что я разместил соответствующие члены над соответствующими частями сети. Поэтому сама сеть является мнемоническим правилом для выражения.

Можете принять это выражение на веру и пропустить его обсуждение прямо до того места, где объясняется, как оно связано с проблемой исчезающего градиента. В этом нет ничего плохого, поскольку это выражение представляет собой особый случай из нашего обсуждения обратного распространения. Однако объяснить его верность легко, поэтому для вас будет достаточно интересно (а, возможно, и поучительно) изучить это объяснение.

Представьте, что мы внесли небольшое изменение Δb₁ в смещение b₁. Это отправит серию каскадных изменений по всей остальной сети. Сначала это заставит измениться выход первого скрытого нейрона Δa₁. Это, в свою очередь, заставить измениться Δz₂ во взвешенном входе на второй скрытый нейрон. Затем произойдёт изменение Δa₂ в выходе второго скрытого нейрона. И так далее, вплоть до изменения ΔC в стоимости выхода. Получится, что:

Это говорит о том, что мы можем вывести выражение для градиента ∂C/∂b₁, тщательно отслеживая влияние каждого шага в этом каскаде.

Для этого подумаем, как Δb₁ заставляет меняться выход a₁ первого скрытого нейрона. Имеем a₁ = σ(z₁) = σ(w₁a₀+b₁), поэтому

Член σ′(z₁) должен выглядеть знакомым: это первый член нашего выражения для градиента ∂C/∂b₁. Интуитивно понятно, что он превращает изменение смещения Δb₁ в изменение Δa₁ выходной активации. Изменение Δa₁ в свою очередь вызывает изменение взвешенного входа z₂ = w₂a₁+b₂ второго скрытого нейрона:

Комбинируя выражения для Δz₂ и Δa₁, мы видим, как изменение смещения b₁ распространяется вдоль сети и влияет на z₂:

И это тоже должно быть знакомо: это два первых члена в нашем заявленном выражении для градиента ∂C/∂b₁.

Так можно продолжать и далее, отслеживая, как изменения распространяются по остальной сети. На каждом нейроне мы подбираем член σ′(z_j), и через каждый вес мы подбираем член w_j. В итоге получается выражение, связывающее конечное изменение ΔC функции стоимости с начальным изменением Δb₁ смещения:

Разделив его на Δb₁, мы действительно получим нужное выражение для градиента:

Почему возникает проблема исчезающего градиента?

Чтобы понять, почему возникает проблема исчезающего градиента, давайте подробно распишем всё наше выражение для градиента:

Кроме последнего члена, это выражение есть произведение членов вида w_jσ′(z_j). Чтобы понять, как ведёт себя каждый из них, посмотрим на график функции σ′:



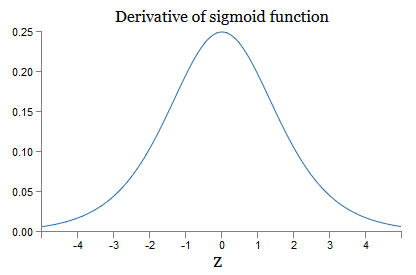
График достигает максимума в точке σ′(0)=1/4. Если мы используем стандартный подход к инициализации весов сети, то мы выбираем веса с использованием распределения Гаусса, то есть, среднеквадратичным нулём и стандартным отклонением 1. Поэтому обычно веса будут удовлетворять неравенству |w_j|<1. Сопоставив все эти наблюдения, увидим, что члены w_jσ′(z_j) обычно будут удовлетворять неравенству |w_jσ′(z_j)|<1/4. А если мы возьмём произведение множества таких членов, то оно будет экспоненциально уменьшаться: чем больше членов, тем меньше произведение. Начинает походить на возможную разгадку проблемы исчезающего градиента.

Чтобы записать это более точно, сравним выражение для ∂C/∂b₁ с выражением градиента относительно следующего смещения, допустим, ∂C/∂b₃. Конечно, мы не записывали подробное выражение для ∂C/∂b₃, но оно следует тем же закономерностям, что описаны выше для ∂C/∂b₁. И вот сравнение двух выражений:



У них есть несколько общих членов. Однако в градиент ∂C/∂b₁ входит два дополнительных члена, каждый из которых имеет вид w_jσ′(z_j). Как мы видели, такие члены обычно не превышают 1/4. Поэтому градиент ∂C/∂b₁ обычно будет в 16 (или больше) раз меньше, чем ∂C/∂b₃. И это основная причина возникновения проблемы исчезающего градиента.

Конечно, это не точное, а неформальное доказательство возникновения проблемы. Существуют несколько оговорок. В частности, можно заинтересоваться тем, будут ли во время обучения расти веса w_j. Если это произойдёт, члены w_jσ′(z_j) в произведении уже не будут удовлетворять неравенству |w_jσ′(z_j)|<1/4. И если они окажутся достаточно большими, больше 1, то у нас уже не будет проблемы исчезающего градиента. Вместо этого градиент будет экспоненциально расти при обратном движении через слои. И вместо проблемы исчезающего градиента мы получим проблему взрывного роста градиента.

Проблема взрывного роста градиента

Давайте посмотрим на конкретный пример возникновения взрывного градиента. Пример будет несколько искусственным: я подстрою параметры сети так, чтобы гарантировать возникновение взрывного роста. Но хотя пример и искусственный, его плюс в том, что он чётко демонстрирует: взрывной рост градиента является не гипотетической возможностью, а может реально случиться.

Для взрывного роста градиента нужно сделать два шага. Сначала мы выберем большие веса во всей сети, допустим, w1=w2=w3=w4=100. Потом мы выберем такие смещения, чтобы члены σ′(z_j) были не слишком маленькими. И это довольно легко сделать: нам нужно лишь выбрать такие смещения, чтобы взвешенный вход каждого нейрона был zj=0 (и тогда σ′(z_j)=1/4). Поэтому, к примеру, нам нужно, чтобы z₁=w₁a₀+b₁=0. Этого можно достичь, назначив b₁=−100∗a₀. Ту же идею можно использовать и для выбора остальных смещений. В итоге мы увидим, что все члены w_jσ′(z_j) окажутся равными 100∗14=25. И тогда у нас получится взрывной рост градиента.

Проблема нестабильного градиента

Фундаментальная проблема заключается не в проблеме исчезающего градиента или взрывном росте градиента. Она в том, что градиент в первых слоях является произведением членов из всех остальных слоёв. И когда слоёв много, ситуация по сути становится нестабильной. И единственный способ, которым все слои смогут обучаться с примерно одной скоростью – это выбрать такие члены произведения, которые будут балансировать друг друга. И при отсутствии некоего механизма или причины для такой балансировки маловероятно, что это произойдёт случайно. Короче говоря, реальная проблема в том, что НС страдают от проблемы нестабильного градиента. И в итоге, если мы будем использовать стандартные обучающие техники на основе градиента, разные слои сети будут обучаться с ужасно разными скоростями.

Упражнение

• В нашем обсуждении проблемы исчезающего градиента мы использовали тот факт, что |σ′(z)|<1/4. Допустим, мы используем другую функцию активации, производная которой может быть гораздо больше. Поможет ли это нам решить проблему нестабильного градиента?

Преобладание проблемы исчезающего градиента

Мы видели, что градиент может исчезать или расти взрывными темпами в первых слоях глубокой сети. На самом деле при использовании сигмоидных нейронов градиент обычно будет исчезать. Чтобы понять, почему, снова рассмотрим выражение |wσ′(z)|. Чтобы избежать проблемы исчезающего градиента, нам нужно, чтобы |wσ′(z)|≥1. Вы можете решить, что этого легко достичь при очень больших значениях w. Однако на самом деле это не так просто. Причина в том, что член σ′(z) тоже зависит от w: σ′(z)=σ′(wa+b), где a – это входная активация. И если мы сделаем w большим, нам надо постараться, чтобы параллельно не сделать σ′(wa+b) маленьким. А это оказывается серьёзным ограничением. Причина в том, что когда мы делаем w большим, мы делаем wa+b очень большим. Если посмотреть на график σ′, видно, что это приводит нас к «крыльям» функции σ′, где она принимает очень малые значения. И единственный способ избежать этого – удерживать входящую активацию в достаточно узком диапазоне значений. Иногда это происходит случайно. Но чаще этого не происходит. Поэтому в общем случае у нас возникает проблема исчезающего градиента.

Задачи

• Рассмотрим результат умножения |wσ′(wa+b)|. Допустим, |wσ′(wa+b)|≥1. Покажите, что это может произойти, только если |w|≥4.
• Предполагая, что |w|≥4, рассмотрите набор входных активаций, для которых |wσ′(wa+b)|≥1.
• Покажите, что набор активаций, удовлетворяющий этому ограничению, может находиться в интервале с шириной не более

  

• Покажите численно, что это выражение сильнее всего ограничивает ширину диапазона при |w|≈6.9, и в этой точке принимает значение ≈0,45. Поэтому, даже если всё будет подобрано идеально, у нас всё равно будет достаточно узкий диапазон входных активаций, способных избежать проблемы исчезающего градиента.
• Тождественный нейрон. Рассмотрим нейрон с одним входом x, соответствующим весом w₁, смещением b и весом w₂ на выходе. Покажите, что правильно выбрав веса и смещение, можно гарантировать, что w₂σ(w₁x+b)≈x for x∈[0,1]. И тогда такой нейрон можно использовать как тождественный, то есть такой, выход которого примерно равен входу (с точностью масштабирования на множитель веса). Подсказка: Полезно переписать x=1/2+Δ, предположить, что w₁ мало, и использовать разложение w₁Δ в ряд Тейлора.

Нестабильность градиентов в более сложных сетях

Мы изучали игрушечные сети всего лишь с одним нейроном в каждом скрытом слое. Что насчёт более сложных глубоких сетей, у которых в каждом скрытом слое есть много нейронов?



На самом деле, в таких сетях происходит примерно то же самое. Ранее в главе про обратное распространение мы видели, что градиент в слое №l сети с L слоями задаётся, как:

Здесь Σ′(z^l) – диагональная матрица, чьи элементы – это значения σ′(z) для взвешенных входов слоя №l. w^l — это матрицы весов для разных слоёв. А ∇_aC – вектор частных производных C по выходным активациям.

Это выражение гораздо сложнее случая с одним нейроном. И всё же, если приглядеться, его суть окажется весьма похожей, с кучей пар вида (w^j)^TΣ′(z^j). Более того, у матриц Σ′(z^j) по диагонали стоят небольшие значения, не больше 1/4. Если весовые матрицы w^j будут не слишком крупными, каждый дополнительный член (w^j)^T Σ′(z^l) склонен уменьшать градиентный вектор, что ведёт к исчезающему градиенту. В общем случае, большее количество членов перемножения ведёт к нестабильному градиенту, как в нашем предыдущем примере. На практике эмпирически обычно в сигмоидных сетях градиенты в первых слоях исчезают экспоненциально быстро. В итоге в этих слоях замедляется обучение. И замедление не является случайностью или неудобством: это фундаментальное следствие избранного нами подхода к обучению.

Другие препятствия на пути к глубокому обучению

В этой главе я сконцентрировался на исчезающих градиентах – и более общем случае нестабильных градиентов – в качестве препятствия на пути к глубокому обучению. На самом деле, нестабильные градиенты – всего лишь одно препятствие для развития ГО, пусть и важное, и фундаментальное. Значительная часть текущих исследований пытается лучше понять проблемы, которые могут возникнуть при обучении ГО. Я не буду подробно описывать все эти работы, однако хочу кратенько упомянуть парочку работ, чтобы дать вам представление о некоторых вопросах, задаваемых людьми.

В качестве первого примера в работе 2010 года было найдено свидетельство тому, что использование сигмоидных функций активации может привести к проблемам с обучением НС. В частности, было обнаружено свидетельство того, что использование сигмоид приведёт к тому, что активации последнего скрытого слоя будут во время обучения насыщаться в районе 0, что будет серьёзно замедлять обучение. Было предложено несколько альтернативных функций активации, не страдающих так сильно от проблемы насыщения (см. также ещё одну работу с обсуждением).

В качестве первого примера в работе 2013 года изучалось влияние на ГО как случайной инициализации весов, так и график импульсов в стохастическом градиентном спуске на основе импульса. В обоих случаях хороший выбор значительно влиял на возможность обучать ГНС.

Эти примеры говорят о том, что вопрос «Почему ГНС так сложно обучать?» очень сложный. В данной главе мы сконцентрировались на нестабильностях, связанных с градиентным обучением ГНС. Результаты двух предыдущих параграфов говорят о том, что роль играет ещё и выбор функции активации, способ инициализации весов и даже детали реализации обучения на основе градиентного спуска. И, естественно, важными будут выбор архитектуры сети и других гиперпараметров. Поэтому множество факторов может сыграть роль в затруднении обучения глубоких сетей, и вопрос понимания этих факторов является объектом текущих исследований. Но всё это кажется довольно мрачным и внушает пессимизм. Однако есть и хорошие новости – в следующей главе мы обернём всё в нашу пользу, и разработаем несколько подходов в ГО, которые до некоторой степени смогут преодолеть или обойти все эти проблемы.