Александр Кушнеров
18.12.2019
Даже опытному инженеру иногда сложно сделать разводку схемы так, чтобы дорожки (или провода) не мешали её правильной работе. В первом приближении, на качество разводки влияет расположение и количество узлов, какие именно провода соединены в каждый из узлов и длина проводов после разветвлений. Если рассматривать длину провода как задержку, то правильная работа асинхронных цифровых схем может не зависеть от задержек в некоторых проводах. В дальнейшем мы будем называть такие провода безопасными, а разветвление таких проводов – полностью безопасным (ПБР). В этой статье мы покажем, как универсальная схема из двенадцати транзисторов может сделать полностью безопасными некоторые разветвления.
Рассмотрим так называемую схему “бабочка” [1], [2] показанную на Рис. 1. Эта схема формирует непересекающиеся импульсы p и q, которые могут использоваться для управления силовыми транзисторами. Буферы на Рис. 1 обозначают безопасные провода. Задержка всех остальных проводов предполагается нулевой. Пауза между импульсами задаётся задержками буферов wy и wz. В дальнейшем мы не будем использовать буфер для обозначения задержки элемента. Провода и разветвления во всех схемах этой статьи проверялись на безопасность (output persistency) в Workcraft [3]. Графы сигнальных переходов (STG) были получены из схем путём разрешения CSC конфликтов. На рисунках показаны упрощённые STG, где сигналы буферов удалены. Временная диаграмма (TD) на Рис. 1 построена по соответствующему STG.
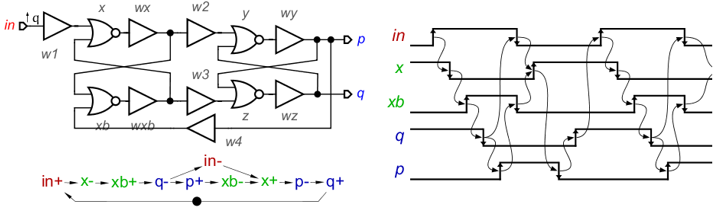
Рис. 1. Схема “бабочка”, её STG и TD в предположении, что задержки в проводах нулевые.
Из теории [1], [2] известно, что схема RS-триггера чувствительна к задержкам проводов в перекрёстной связи. Именно поэтому буферы в перекрёстных связях на Рис. 1 отсутствуют. Таким образом, два элемента триггера должны находиться на минимальном расстоянии друг от друга. Если это трудно сделать, то два элемента можно заменить на один сложный элемент с обратной связью. Например, элементы x и xb в схеме “бабочка” можно заменить как показано на Рис. 2. В дополнение мы получаем ПБР на выходе сложного элемента.
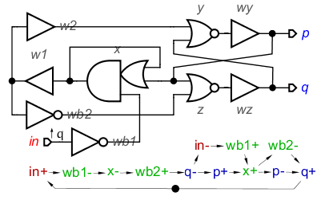
Рис. 2. Вариант схемы на Рис. 1 и его STG в предположении, что задержки в проводах нулевые.
Реализация схем на Рис. 1 и Рис. 2 требует 16 и 20 транзисторов соответственно. Кроме того, схема на Рис. 2 медленнее, поскольку инверторы wb1, wb2 и инвертор внутри элемента 2ИЛИ-И должны переключиться два раза за цикл. Снижение быстродействия, как правило, является ценой за ПБР. Однако, у этого правила есть исключения. Например, на Рис. 3 показана схема асинхронного счётного триггера (АСТ) [4] которая имеет два ПБР.

Рис. 3. АСТ и его STG в предположении, что задержки в проводах нулевые.
Недостатками схемы на Рис. 3 являются большое число проводов и то, что большинство из них пересекаются. Это может осложнить разводку, особенно если количество слоёв с дорожками ограниченно или они заняты другими соединениями. Таким образом, нужно искать некоторый компромисс между количеством проводов, количеством транзисторов и количеством ПБР. Примером такой компромиссной схемы с одним ПБР является АСТ показанный на Рис. 4. Это небольшая модификация схемы из [5]. Заметим, что здесь, как и в схеме на Рис. 2, используется смешанный базис. Для реализации этого АСТ без индикатора (XOR на wi2, wi4 и g5) нужно 26 транзисторов. Это всего на два транзистора больше по сравнению с АСТ на Рис. 3.

Рис. 4. Компромиссный АСТ и его STG, когда задержки в проводах нулевые.
Заметим, что все элементы с обратной связью на Рис. 2 и Рис. 4 – это частные случаи обобщённого C-элемента (gC). Он задаётся как [6]: , где
, где  и
и  – это функции установки и сброса, удовлетворяющие условию
– это функции установки и сброса, удовлетворяющие условию  . Частными случаями gC-элемента также являются NCL-элементы, которые используются в схемах для обработки данных. Заметим, что самый большой NCL-элемент имеет четыре входа и реализуется на 28 транзисторах [7]. Это можно объяснить тем, что при большем числе транзисторов провода становятся относительно длинными и задержка в них начинает влиять на работу элемента.
. Частными случаями gC-элемента также являются NCL-элементы, которые используются в схемах для обработки данных. Заметим, что самый большой NCL-элемент имеет четыре входа и реализуется на 28 транзисторах [7]. Это можно объяснить тем, что при большем числе транзисторов провода становятся относительно длинными и задержка в них начинает влиять на работу элемента.
Рассмотрим транзисторную схему, показанную на Рис. 5. Она реализует функцию пяти переменных [8], [9] . В таблице 1 приведены СДНФ и СКНФ функции
. В таблице 1 приведены СДНФ и СКНФ функции  и её двойственной функции
и её двойственной функции  . Из этой таблицы очевидно, что поменяв местами
. Из этой таблицы очевидно, что поменяв местами  и
и  в
в  , мы получим
, мы получим  и наоборот. В случае если
и наоборот. В случае если  , мы получим самодвойственную функцию
, мы получим самодвойственную функцию  .
.
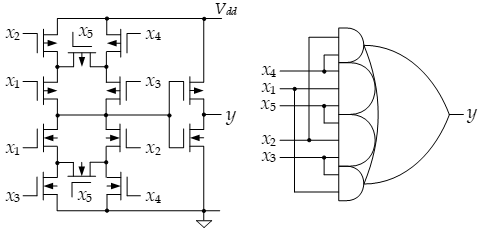
Рис. 5. Схема, реализующая функцию пяти переменных.
Таблица 1. Формы логических функций для схемы на Рис. 5.

Заметим, что означает, что соответствующие четыре транзистора должны переключаться одновременно. Даже если провода после разветвления y имеют одинаковую задержку, этого не достаточно, поскольку момент переключения транзистора определяется напряжением на его затворе. С этой точки зрения анализ схемы на Рис. 5 был сделан в [10]. Однако, этот анализ не полный, поскольку рассматривалась только реализация двухвходового С-элемента. Чтобы сделать полный анализ, нужно сначала найти все варианты объединения входов или, более формально, все функции меньшего числа переменных, которые могут быть получены из
означает, что соответствующие четыре транзистора должны переключаться одновременно. Даже если провода после разветвления y имеют одинаковую задержку, этого не достаточно, поскольку момент переключения транзистора определяется напряжением на его затворе. С этой точки зрения анализ схемы на Рис. 5 был сделан в [10]. Однако, этот анализ не полный, поскольку рассматривалась только реализация двухвходового С-элемента. Чтобы сделать полный анализ, нужно сначала найти все варианты объединения входов или, более формально, все функции меньшего числа переменных, которые могут быть получены из  . Такой поиск был выполнен в несколько упрощённом виде, и его результаты приведены в приложении. Большинство функций найдено в нескольких вариантах. Из них нужно выбрать такие, которые дают схемы свободные от состязаний [11]. Все полученные функции, число вариантов каждой из них и номер соответствующей таблицы в приложении приведены в таблице 2. Номерами со звёздочкой обозначены двойственные функции.
. Такой поиск был выполнен в несколько упрощённом виде, и его результаты приведены в приложении. Большинство функций найдено в нескольких вариантах. Из них нужно выбрать такие, которые дают схемы свободные от состязаний [11]. Все полученные функции, число вариантов каждой из них и номер соответствующей таблицы в приложении приведены в таблице 2. Номерами со звёздочкой обозначены двойственные функции.
Таблица 2. gC-элементы, реализуемые схемой на Рис. 5.

Функции 2 и 2*, 5 и 5*, 7 и 7* являются самодвойственными, а функцию 4 можно получить из функции 4* поменяв местами a и c. Заметим, что кроме функции 6* все остальные функции пороговые. Это можно объяснить тем, что является изотонной (positive unate) и тем, что для четырёх и менее переменных изотонные функции совпадают с псевдопороговыми [12]. Вопрос о том, какие варианты есть для функций 1*, 3* и 6* в этой статье остаётся открытым.
является изотонной (positive unate) и тем, что для четырёх и менее переменных изотонные функции совпадают с псевдопороговыми [12]. Вопрос о том, какие варианты есть для функций 1*, 3* и 6* в этой статье остаётся открытым.
Рассмотрим случай с функциями 2 и 2* на примере. В соответствии с одним из вариантов (таблица П3 в приложении) и
и  . Пусть выход
. Пусть выход  отключён от входa
отключён от входa  и пусть сигнал снимается со входа инвертора. Это позволяет построить ячейку конвейерного распределителя [13] показанную на Рис. 6. Элементы в этой ячейке разные, но из-за того, что входы объединены, они оба реализуют одну и ту же самодвойственную функцию. Заметим, что элементы с перекрёстной связью в схемах на Рис. 1, на Рис. 3 и на Рис. 6 являются частными случаями базовой конструкции для совершенной реализации [2]. Таким образом, должны существовать правила для преобразования схем базовой конструкции в схемы на gC-элементах и наоборот.
и пусть сигнал снимается со входа инвертора. Это позволяет построить ячейку конвейерного распределителя [13] показанную на Рис. 6. Элементы в этой ячейке разные, но из-за того, что входы объединены, они оба реализуют одну и ту же самодвойственную функцию. Заметим, что элементы с перекрёстной связью в схемах на Рис. 1, на Рис. 3 и на Рис. 6 являются частными случаями базовой конструкции для совершенной реализации [2]. Таким образом, должны существовать правила для преобразования схем базовой конструкции в схемы на gC-элементах и наоборот.

Рис. 6. Ячейка конвейерного распределителя.
С точки зрения технологии, транзисторы должны быть “нанизаны” на поликремниевые шины. Такая реализация схемы на Рис. 5 приведена в [14]. Для установки начальных состояний можно использовать p-MOS и n-MOS транзисторы, создающие с транзисторами в инверторе делитель напряжения. Помехоустойчивость схем можно увеличить с помощью определённых преобразований STG [15].
Автор глубоко признателен Светлане Фроловой (ОмГУ) за сканирование статьи [1], а также Сергею Быстрову за вдохновение.
Для получения представленных в этом разделе результатов был использован MuPAD. Пусть выход y соединён только с одним из входов. Таблица П1 показывает, что в этом случае . Чтобы получить функции для которых
. Чтобы получить функции для которых  , можно либо объединить некоторые переменные, либо присвоить им константы. Функции для случая объединения двух переменных приведены в таблице П2. Другие варианты не дают
, можно либо объединить некоторые переменные, либо присвоить им константы. Функции для случая объединения двух переменных приведены в таблице П2. Другие варианты не дают  . Поскольку первые четыре функции в таблице П1 совпадают с точностью до перестановки переменных, мы будем рассматривать только первую и пятую. Случаи
. Поскольку первые четыре функции в таблице П1 совпадают с точностью до перестановки переменных, мы будем рассматривать только первую и пятую. Случаи  и
и  не интересны, поскольку в первом мы можем только сбросить gC-элемент, но не можем его установить, а во втором – наоборот. Манипуляции с переменными позволили получить из таблицы П1 функции четырёх и трёх переменных, которые приведены таблице П3 и таблице П4 соответств��нно.
не интересны, поскольку в первом мы можем только сбросить gC-элемент, но не можем его установить, а во втором – наоборот. Манипуляции с переменными позволили получить из таблицы П1 функции четырёх и трёх переменных, которые приведены таблице П3 и таблице П4 соответств��нно.
Таблица П1. Функции пяти переменных.
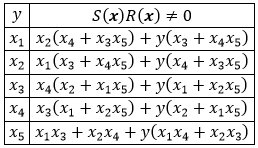
Таблица П2. Функции четырёх переменных.

Таблица П3. Функции четырёх переменных, полученные из Таблицы П1.

Таблица П4. Функции трёх переменных, полученные из Таблицы П1.

[1] В. И. Варшавский, М. А. Кишиневский, А. Р. Таубин and Б. С. Цирлин, «Анализ асинхронных логических схем. II. Достижимость рабочих состояний и влияние задержек в проводах,» Изв. АН СССР. Техническая кибернетика, no. 4, pp. 84-97, 1982.
[2] Варшавский, В. И. (ред.), Автоматное управление асинхронными процессами в ЭВМ и дискретных системах, Наука, 1986.
[3] workcraft.org.
[4] R. C. Todd, «Logic system». Patent US3609569, 28 Sep. 1971.
[5] E. A. Vittoz, «Frequency dividing logic structure». Patent US3829714, 13 Aug. 1974.
[6] J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno and A. Yakovlev, Logic synthesis for asynchronous controllers and interfaces, Springer, 2002.
[7] A. Kondratyev, «Multi-rail asynchronous flow with completion detection and system and method for designing the same». Patent US6526542, 25 Feb. 2003.
[8] J. J. Gibson, «Logic circuits employing field-effect transistors». Patent US3439185, 15 Apr. 1969.
[9] Р. Миллер, Теория переключательных схем. Том I. Комбинационные схемы, Наука, 1970.
[10] K. van Berkel, «Beware the isochronic fork,» Integration, vol. 13, no. 2, pp. 103-128, 1992.
[11] P. Kudva, G. Gopalakrishnan, H. Jacobson and S. M. Nowick, «Synthesis of hazard-free customized CMOS complex-gate networks under multiple-input changes,» in Design Automation Conf., 1996.
[12] G. W. Fagerlin, Enumeration of pseudo-separable functions of five variables. M.Sc. thesis, University of Illinois, 1968.
[13] В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко and Б. С. Цирлин, «Асинхронный распределитель». Patent SU1598142, 07 10 1990.
[14] S. W. Cheng, «H-tree CMOS logic circuit,» in IEEE Conf. on Electronics, Circuits and Systems, 2008.
[15] A. Taubin, A. Kondratyev, J. Cortadella and L. Lavagno, «Behavioral transformations to increase noise immunity in asynchronous specifications,» in IEEE Symp. on Async. Circuits and Systems, 1999.
18.12.2019
Даже опытному инженеру иногда сложно сделать разводку схемы так, чтобы дорожки (или провода) не мешали её правильной работе. В первом приближении, на качество разводки влияет расположение и количество узлов, какие именно провода соединены в каждый из узлов и длина проводов после разветвлений. Если рассматривать длину провода как задержку, то правильная работа асинхронных цифровых схем может не зависеть от задержек в некоторых проводах. В дальнейшем мы будем называть такие провода безопасными, а разветвление таких проводов – полностью безопасным (ПБР). В этой статье мы покажем, как универсальная схема из двенадцати транзисторов может сделать полностью безопасными некоторые разветвления.
Рассмотрим так называемую схему “бабочка” [1], [2] показанную на Рис. 1. Эта схема формирует непересекающиеся импульсы p и q, которые могут использоваться для управления силовыми транзисторами. Буферы на Рис. 1 обозначают безопасные провода. Задержка всех остальных проводов предполагается нулевой. Пауза между импульсами задаётся задержками буферов wy и wz. В дальнейшем мы не будем использовать буфер для обозначения задержки элемента. Провода и разветвления во всех схемах этой статьи проверялись на безопасность (output persistency) в Workcraft [3]. Графы сигнальных переходов (STG) были получены из схем путём разрешения CSC конфликтов. На рисунках показаны упрощённые STG, где сигналы буферов удалены. Временная диаграмма (TD) на Рис. 1 построена по соответствующему STG.

Рис. 1. Схема “бабочка”, её STG и TD в предположении, что задержки в проводах нулевые.
Из теории [1], [2] известно, что схема RS-триггера чувствительна к задержкам проводов в перекрёстной связи. Именно поэтому буферы в перекрёстных связях на Рис. 1 отсутствуют. Таким образом, два элемента триггера должны находиться на минимальном расстоянии друг от друга. Если это трудно сделать, то два элемента можно заменить на один сложный элемент с обратной связью. Например, элементы x и xb в схеме “бабочка” можно заменить как показано на Рис. 2. В дополнение мы получаем ПБР на выходе сложного элемента.

Рис. 2. Вариант схемы на Рис. 1 и его STG в предположении, что задержки в проводах нулевые.
Реализация схем на Рис. 1 и Рис. 2 требует 16 и 20 транзисторов соответственно. Кроме того, схема на Рис. 2 медленнее, поскольку инверторы wb1, wb2 и инвертор внутри элемента 2ИЛИ-И должны переключиться два раза за цикл. Снижение быстродействия, как правило, является ценой за ПБР. Однако, у этого правила есть исключения. Например, на Рис. 3 показана схема асинхронного счётного триггера (АСТ) [4] которая имеет два ПБР.

Рис. 3. АСТ и его STG в предположении, что задержки в проводах нулевые.
Недостатками схемы на Рис. 3 являются большое число проводов и то, что большинство из них пересекаются. Это может осложнить разводку, особенно если количество слоёв с дорожками ограниченно или они заняты другими соединениями. Таким образом, нужно искать некоторый компромисс между количеством проводов, количеством транзисторов и количеством ПБР. Примером такой компромиссной схемы с одним ПБР является АСТ показанный на Рис. 4. Это небольшая модификация схемы из [5]. Заметим, что здесь, как и в схеме на Рис. 2, используется смешанный базис. Для реализации этого АСТ без индикатора (XOR на wi2, wi4 и g5) нужно 26 транзисторов. Это всего на два транзистора больше по сравнению с АСТ на Рис. 3.

Рис. 4. Компромиссный АСТ и его STG, когда задержки в проводах нулевые.
Заметим, что все элементы с обратной связью на Рис. 2 и Рис. 4 – это частные случаи обобщённого C-элемента (gC). Он задаётся как [6]:
Рассмотрим транзисторную схему, показанную на Рис. 5. Она реализует функцию пяти переменных [8], [9]

Рис. 5. Схема, реализующая функцию пяти переменных.
Таблица 1. Формы логических функций для схемы на Рис. 5.

Заметим, что
Таблица 2. gC-элементы, реализуемые схемой на Рис. 5.

Функции 2 и 2*, 5 и 5*, 7 и 7* являются самодвойственными, а функцию 4 можно получить из функции 4* поменяв местами a и c. Заметим, что кроме функции 6* все остальные функции пороговые. Это можно объяснить тем, что
Рассмотрим случай с функциями 2 и 2* на примере. В соответствии с одним из вариантов (таблица П3 в приложении)

Рис. 6. Ячейка конвейерного распределителя.
С точки зрения технологии, транзисторы должны быть “нанизаны” на поликремниевые шины. Такая реализация схемы на Рис. 5 приведена в [14]. Для установки начальных состояний можно использовать p-MOS и n-MOS транзисторы, создающие с транзисторами в инверторе делитель напряжения. Помехоустойчивость схем можно увеличить с помощью определённых преобразований STG [15].
Благодарности
Автор глубоко признателен Светлане Фроловой (ОмГУ) за сканирование статьи [1], а также Сергею Быстрову за вдохновение.
Приложение
Для получения представленных в этом разделе результатов был использован MuPAD. Пусть выход y соединён только с одним из входов. Таблица П1 показывает, что в этом случае
Таблица П1. Функции пяти переменных.
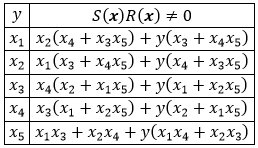
Таблица П2. Функции четырёх переменных.

Таблица П3. Функции четырёх переменных, полученные из Таблицы П1.

Таблица П4. Функции трёх переменных, полученные из Таблицы П1.

Литература
[1] В. И. Варшавский, М. А. Кишиневский, А. Р. Таубин and Б. С. Цирлин, «Анализ асинхронных логических схем. II. Достижимость рабочих состояний и влияние задержек в проводах,» Изв. АН СССР. Техническая кибернетика, no. 4, pp. 84-97, 1982.
[2] Варшавский, В. И. (ред.), Автоматное управление асинхронными процессами в ЭВМ и дискретных системах, Наука, 1986.
[3] workcraft.org.
[4] R. C. Todd, «Logic system». Patent US3609569, 28 Sep. 1971.
[5] E. A. Vittoz, «Frequency dividing logic structure». Patent US3829714, 13 Aug. 1974.
[6] J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno and A. Yakovlev, Logic synthesis for asynchronous controllers and interfaces, Springer, 2002.
[7] A. Kondratyev, «Multi-rail asynchronous flow with completion detection and system and method for designing the same». Patent US6526542, 25 Feb. 2003.
[8] J. J. Gibson, «Logic circuits employing field-effect transistors». Patent US3439185, 15 Apr. 1969.
[9] Р. Миллер, Теория переключательных схем. Том I. Комбинационные схемы, Наука, 1970.
[10] K. van Berkel, «Beware the isochronic fork,» Integration, vol. 13, no. 2, pp. 103-128, 1992.
[11] P. Kudva, G. Gopalakrishnan, H. Jacobson and S. M. Nowick, «Synthesis of hazard-free customized CMOS complex-gate networks under multiple-input changes,» in Design Automation Conf., 1996.
[12] G. W. Fagerlin, Enumeration of pseudo-separable functions of five variables. M.Sc. thesis, University of Illinois, 1968.
[13] В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко and Б. С. Цирлин, «Асинхронный распределитель». Patent SU1598142, 07 10 1990.
[14] S. W. Cheng, «H-tree CMOS logic circuit,» in IEEE Conf. on Electronics, Circuits and Systems, 2008.
[15] A. Taubin, A. Kondratyev, J. Cortadella and L. Lavagno, «Behavioral transformations to increase noise immunity in asynchronous specifications,» in IEEE Symp. on Async. Circuits and Systems, 1999.
