Продолжая серию статей про технологию zk-SNARKs изучаем очень интересную статью Виталика Бутерина "Quadratic Arithmetic Programs: from Zero to Hero"
Предыдущая статья: Введение в zk-SNARKs с примерами (перевод)
В последнее время интерес к технологии zk-SNARKs очень вырос, и люди все чаще пытаются демистифицировать то, что многие стали называть «лунной математикой» из-за своей достаточно неразборчивой сложности. zk-SNARKs действительно довольно сложно понять, особенно из-за большого количества составных частей, которые нужно собрать вместе, чтобы все это работало, но если мы разберем технологию по частям, то осмыслить ее станет гораздо проще...
Целью данной публикации — не является полное введение в технологию zk-SNARK. Также предполагается, что, во-первых, вы знаете, что такое zk-SNARKs и что они делают, и во-вторых, достаточно хорошо знаете математику, чтобы иметь возможность рассуждать о таких вещах, как полиномы (если утверждение P(x) + Q(x) = (P + Q)(x), где P и Q являются полиномами, кажется естественным и очевидным для вас, то ваш уровень достаточен). Скорее, данная публикация раскрывает механизм, стоящий за технологией, и пытается объяснить, насколько это возможно, первую половину преобразований, показанных исследователем zk-SNARKs Эран Тромером (Eran Tromer):

Преобразования здесь можно разбить на две составляющие. Во-первых, zk-SNARKs не могут применяться к какой-либо вычислительной проблеме напрямую; сначала вам нужно преобразовать задачу в правильную «форму» для проблемы, которую она решает. Форма называется «квадратичной арифметической программой» (QAP), и преобразование кода функции в такую форму само по себе весьма нетривиальная задача. Наряду с преобразования кода функции в QAP, есть еще одно отдельное действие, которое выполняется, если у вас есть входной аргумент для преобразовываемой функции. Вам нужно создать соответствующее решение (иногда называемое "свидетельством" для QAP). Также существует еще один довольно сложный механизм для создания фактического «доказательства с нулевым разглашением» для этого свидетельства и отдельный процесс проверки доказательства того, что передали вам, но это отдельный разговор, выходящий за пределы данной публикации. (Для понимания общей схемы процесса, смотрите первую статью. прим. переводчика).
Мы разберем простой пример: необходимо доказать, что вы знаете решение кубического уравнения:
(подсказка: ответ 3). Эта задача достаточно проста, поэтому полученный QAP не будет настолько большим, чтобы испугать вас. Но код будет достаточно нетривиальным, чтобы вы могли увидеть всю математику в действии.
Опишем нашу функцию следующим образом:
def qeval(x):
y = x**3
return x + y + 5Используемый здесь простой язык программирования специального назначения поддерживает базовую арифметику (+, -, *, /), ограниченное возведение в степень (x**7, но не x**y) и присваивание переменным, которое является достаточно мощным инструментом, позволяя вам в теории производить вычисления внутри функции (пока число шагов вычислений ограничено и не допускается использование циклов). Обратите внимание, что деление по модулю (%) и операторы сравнения (<,>, ≤, ≥) не поддерживаются, так как нет эффективного способа производить деление по модулю или сравнения непосредственно в законченной циклической групповой арифметике (будьте благодарны за это, так как если бы был способ реализовать одну из этих операций, криптография на эллиптических кривых была бы взломана быстрее, чем бы вы произнесли «бинарный поиск» и «китайская теорема об остатках»).
Вы можете расширить язык до деления по модулю и сравнений, используя разложение на биты, например:
в качестве вспомогательных параметров, проверив правильность этих разложений и выполнив математику в двоичных операциях; в арифметике конечного поля проверка равенства (==) также выполнима и даже намного проще, но мы не будем заниматься сейчас этими вещами. Мы можем расширить язык для поддержки условных выражений (например,
if x < 5: y = 7; else: y = 9) путем преобразования их в арифметическую форму y = 7 * (x < 5) + 9 * (x >= 5); но обратите внимание, что при этом обе ветви условного выражения должны быть выполнены, и если у вас много вложенных условий, это приведет к росту накладных расходов.Давайте теперь выполним процесс преобразования в QAP шаг за шагом. Если вы хотите сделать это самостоятельно для любого кода, я реализовал компилятор здесь (только для образовательных целей, и он еще не готов к созданию QAP для реальных zk-SNARKs!).
Упрощение
Первым шагом является процедура «упрощения». В ней мы преобразуем исходный код, который может содержать произвольное число сложных операторов и выражений, в последовательность операторов, которые имеют две формы:
x = y (где y может быть переменная или число) и
x = y (op) z (где op может быть +, -, *, /; y и z могут быть переменными, числами или подвыражениями).
Вы можете представить каждый из этих операторов как логический переход в цепи (имеется ввиду "логический вентиль", меняющий состояния. Прим. переводчика). Результатом процесса упрощения для вышеуказанного кода является следующее:
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5Если вы посмотрите исходный код и код выше, вы можете легко увидеть, что они эквивалентны.
Переход в R1CS
Теперь мы преобразуем это в то, что называется "Системой Ограничения Ранга-1" (R1CS). R1CS представляет собой последовательность групп из трех векторов (a, b, c), а решение R1CS представляет собой вектор s, где s должно удовлетворять уравнению s.a * s.b - s.c = 0, где . представляет собой "взятие точки" (перемножение вектора строки на вектор столбец. Прим. переводчика). Говоря простым языком, если мы «скомпонуем» a и s, умножая значения векторов в одних и тех же позициях, а затем возьмем сумму этих произведений, затем сделаем то же самое для b и, s а затем, то же самое для c и s, то в итоге третий результат будет равен произведению первых двух результатов. Пример решения R1CS:
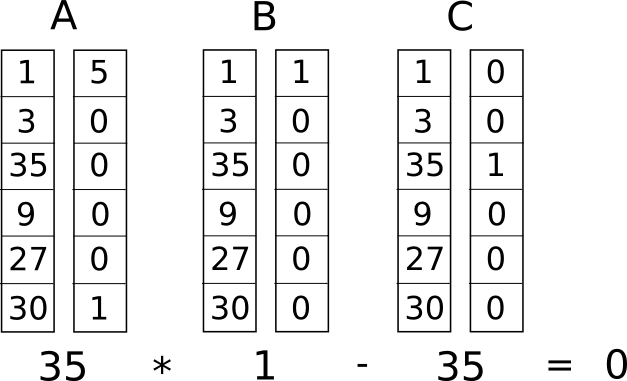
Но вместо того, чтобы иметь только одно ограничение в программе, мы введем множество ограничений: по одному для каждого логического перехода. Существует стандартный способ преобразования логического перехода в (a, b, c) тройку, в зависимости от того, какая операция выполняется (+, -, * или /), и являются ли аргументы переменными или числами. Длина каждого вектора равна общему числу переменных в системе, которое включает в себя фиктивную переменную ~one в имеющую значение 1, входные параметры, фиктивную переменную ~out, представляющую результат, а также все промежуточные переменные ( sym1 и sym2 см. выше); Вектора, как правило, будут очень "разряженными", с заполненными значениями, соответствующие переменным, на которые воздействует какой-то конкретный логический переход.
Давайте обозначим список переменных, которые мы будем использовать:
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'
Вектор решения будет состоять из присваивания значений для всех этих переменных в аналогичном порядке.
Теперь мы найдем (a, b, c) тройку для первого перехода:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]Легко убедиться в том, что если значение вектора решения во второй позиции равно 3, а в четвертой позиции равно 9, то независимо от остальных значений вектора решения проверка вектора сократится до 3*3 = 9 и решение окажется верным. Если значение вектора решения равно -3 во второй позиции и 9 в четвертой, то проверка также будет успешной. То же верно и для значения 7 во второй позиции и 49 в четвертой. Цель этой первой проверки — убедиться в согласованности входов и выходов только первого перехода.
Теперь давайте перейдем ко второму переходу:
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]Аналогично первой проверке, здесь мы проверяем sym_1 * x = y
Третий переход:
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]Здесь шаблон несколько отличается: он умножает первый элемент в векторе решения на второй элемент, затем на пятый элемент, складывая два результата и проверяя, равна ли сумма шестому элементу. Поскольку первый элемент в векторе решения всегда равен единице, это просто проверка сложения, подтверждающая, что выход равен сумме двух входов.
Наконец, четвертый переход:
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]Здесь мы воспроизводим последнюю проверку ~out = sym_2 + 5. Проверка работает, беря шестой элемент в векторе решения, добавляя первый элемент, умноженный на 5 (напоминаем: первый элемент равен 1, поэтому это фактически означает добавление 5) и соотнося его с третьим элементом, где мы храним выходную переменную.
Итак, у нас есть R1CS с четырьмя ограничениями. Свидетельством является просто значение всех переменных, включая входные, выходные и внутренние переменные:
[1, 3, 35, 9, 27, 30]Вы можете вычислить это сами, просто «выполнив» упрощенный код выше, начиная с назначения входных переменных x = 3, введя значения всех промежуточных переменных и изменяя их в процессе вычислений.
Теперь приведем полностью R1CS для нашего случая:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]R1CS — QAP
Следующим шагом является преобразование данной R1CS в форму QAP, которая реализует ту же логику, но вместо "взятия точки" будут использоваться полиномы. Мы сделаем это следующим образом: мы перейдем от четырех групп из трех векторов длиной в шесть к шести группам из трех полиномов 3-й степени, где каждая координата x полинома соответствует одному из ограничений. То есть, если мы вычислим значения многочленов при x = 1, то мы получим наш первый набор векторов, если вычислить многочлены от x = 2, тогда мы получим второй набор векторов и т.д.
Мы можем сделать это преобразование, используя например, интерполяционный многочлен Лагранжа. Проблема, которую решает интерполяция Лагранжа, такова: если у вас есть набор точек (т.е. (x, y) координатных пар), то выполнение интерполяции Лагранжа в этих точках дает вам многочлен, проходящий через все эти точки. Мы делаем это, разбивая задачу следующим образом: для каждого значения x мы создаем многочлен, который возвращает y значение, соответствующее заданной точке (x, y) и возвращает 0 во всех остальных случаях. А затем, для получения конечного результата мы складываем все многочлены.
Приведем пример. Предположим, что нам нужен полином, проходящий через (1, 3), (2, 2) и (3, 4). Начнем с создания полинома, проходящего через (1, 3), (2, 0) и (3, 0). Как оказалось, сделать многочлен, принимающий значение только при x = 1 и равный нулю в других случаях, очень просто:
(x - 2) * (x - 3)На графике это выглядит так:
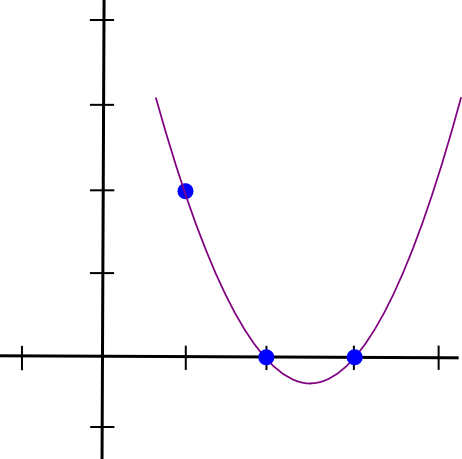
Теперь нам просто нужно "изменить масштаб" для того, чтобы высота в точке x = 1 была нужной:
(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))Это даст нам:

Затем мы делаем все то же самое с двумя другими точками и получаем два других аналогичных полинома, за исключением того, что они принимают значения при x = 2 и x = 3 вместо x = 1.
Мы складываем все три полинома вместе и получаем:
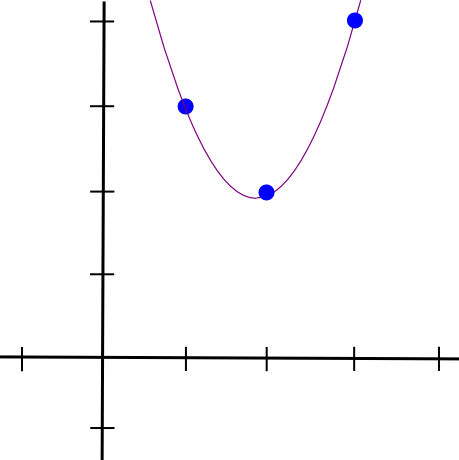
Это как раз то что нам нужно. Сложность по времени выполнения вышеописанного алгоритма O (n^3), так как существует n точек, и каждая точка требует O (n^2) времени для перемножения многочленов. Немного оптимизировав, сложность может быть сведена к O (n^2). А если использовать быстрые алгоритмы преобразования Фурье и т. п., сложность можно еще уменьшить — это существенно оптимизирует zk-SNARKs, т.к. на практике реальные функции могут содержать тысячи переходов.
Теперь давайте преобразуем нашу R1CS в интерполяционный многочлен Лагранжа. Мы возьмем значение первой позиции из каждого вектора a, применим интерполяцию Лагранжа, чтобы получить полином (где вычисление значения полинома в точке i даст значение i-го вектора a в первой позиции). Далее повторим процесс для значения первой позиции каждого вектора b и c, а затем повторим этот процесс для последующих позиций. Для удобства я покажу вам сразу результат:
Полином A
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
Полином B
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
Полином C
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]Коэффициенты отсортированы в порядке возрастания степени, поэтому первый многочлен должен быть: 0.833 x^3 — 5x^2 + 9.166*x — 5. Этот набор многочленов (плюс многочлен Z, смысл которого я объясню позже) является параметрами нашего экземпляра QAP. Обратите внимание, что все необходимые действия до данного момента выполняются только один раз для одной и той же функции, которую вы собираетесь использовать для проверки zk-SNARKs. Как только параметры QAP сгенерированы, их можно повторно использовать.
Попробуем посчитать все эти многочлены при x = 1. Оценка полинома при x = 1 просто означает сложение всех коэффициентов (так как 1^k = 1 для любого k), поэтому это не является сложной задачей. Мы получим:
результат A для x=1
0
1
0
0
0
0
результат B для x=1
0
1
0
0
0
0
результат C для x=1
0
0
0
1
0
0Здесь мы получили такой же набор трех векторов для первого логического перехода, который мы создали выше.
Проверка QAP
Теперь давайте разберемся, в чем смысл всех этих сумасшедших трансформаций? Ответ заключается в том, что вместо проверки ограничений в R1CS индивидуально, мы можем теперь проверить все ограничения одновременно, выполнив проверку "взятия точки" на полиномах.

Поскольку в этом случае проверка "взятия точки" представляет собой ряд сложений и умножений многочленов, результат сам по себе будет многочленом. Если полученный многочлен, вычисленный в каждой координате x, которую мы использовали выше для представления логического перехода, равен нулю, то это означает, что все проверки проходят. Если результирующий многочлен дает ненулевое значение хотя бы на одной из координат x, представляющей логический переход, это означает, что входные и выходные значения являются несогласованными для данного логического перехода (например переход y = x*sym_1, а предоставлены значения, например x = 2, sym_1 = 2 и y = 5).
Заметим, что полученный многочлен не должен принимать ноль для любых значений. Как правило, в большинстве случаев значения будут отличаться от нуля. Его поведение может быть любым в точках, отличных от логических переходов, но он должен принимать значение ноль во всех точках, которые действительно соответствуют логическим переходам. Чтобы проверить правильность всего решения, мы не будем оценивать полином t = A.s * B.s - C.s в каждой точке, соответствующей переходу. Вместо этого мы делим t на другой многочлен, Z и проверяем, что Z полностью делит t, то есть деление t / Z происходит без остатка.
Z определяется как (x - 1) * (x - 2) * (x - 3) ... — простейший многочлен, равный нулю во всех точках, соответствующих логическим переходам. Как известно из математики, любой многочлен, равный нулю во всех этих точках, должен быть кратным "минимальному" многочлену для этих точек. И наоборот, если многочлен кратен Z, то его значение в любой из этих точек будет равно нулю. Эта эквивалентность упрощает наши вычисления.
Теперь давайте сделаем проверку "взятия точки" с указанными выше полиномами. Во-первых, промежуточные многочлены:
A.s = [43.0, -73.333, 38.5, -5.166]
B.s = [-3.0, 10.333, -5.0, 0.666]
C.s = [-41.0, 71.666, -24.5, 2.833]Теперь вычислим A.s * B.s - C.s:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Вычислим "минимальный" многочлен Z = (x - 1) * (x - 2) * (x - 3) * (x - 4):
Z = [24, -50, 35, -10, 1]И если мы разделим результат выше на Z, получим:
h = t / Z = [-3.666, 17.055, -3.444]Как видите, без остатка.
Итак, у нас есть решение для QAP. Если мы попытаемся изменить любую из переменных в решении R1CS, которую мы получили для этого решения QAP, например, установить последнее значение 31 вместо 30, то мы получим полином t, который не пройдет одну из проверок (в этом конкретном случае, результат при x = 3 будет равен -1 вместо 0). Кроме того t не будет кратным Z. Деление t / Z даст остаток [-5.0, 8.833, -4.5, 0.666].
Обратите внимание, что приведенное выше является упрощением. В "реальном мире" добавление, умножение, вычитание и деление произойдет не с регулярными числами, а с элементами конечного поля — жуткий вид арифметики, который является самосогласованным, поэтому все алгебраические законы, которые мы знаем и любим там еще действительны. Но в все ответы там являются элементами некоторого набора конечного размера, обычно целые числа в диапазоне от 0 до n-1 для некоторого n. Например, если n = 13, то 1/2 = 7 (и 7 2 = 1), 3 5 = 2 и т.д.
Использование арифметики с конечным полем избавляет нас о беспокойстве за ошибки округления и позволяет системе хорошо работать с эллиптическими кривыми, которые в конечном итоге необходимы для остальной части zk-SNARKs, что делает протокол zk-SNARKs фактически безопасным.
Особая благодарность Эрану Тромеру за то, что он помог мне объяснить многие подробности о внутренней работе zk-SNARKs.
