В 1961-м году Рольф Ландауэр в своей статье «Irreversibility and heat generation in the computing process» сформулировал принцип, согласно которому в любой вычислительной системе, независимо от её физической реализации, при потере 1 бита информации выделяется теплота в количестве по крайней мере W = kB T ln2, где kB − постоянная Больцмана, а T − температура вычислительной системы в кельвинах.
То есть если вычисление производится при комнатной температуре (300K), то при потере 1 бита данных вычислительная система не может не рассеять в окружающее пространство примерно 2,7×10-21 Дж.
Считается, что единственный способ преодолеть это ограничение − использовать так называемые обратимые вычисления. В этой статье я докажу, что принцип Ландауэра не является догмой, и преодоление устанавливаемого им барьера возможно в том числе и без использования обратимых вычислений.
Ключ к пониманию того, из чего следует принцип Ландауэра − во фразе "A simple binary device consists of a particle in a bistable potential well" (простейшее двоичное устройство состоит из частицы в двухстабильной потенциальной яме):
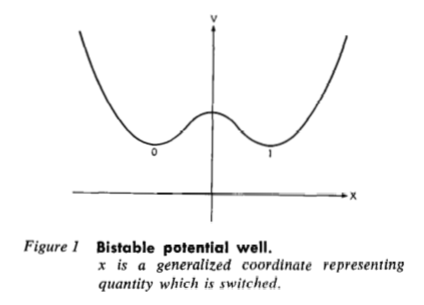
Для того, чтобы переключить систему с состояния «0» в состояние «1» (или наоборот), мы должны:
1. Придать частице энергию, достаточную для преодоления барьера.
2. Отобрать у частицы энергию для того, чтобы частица зафиксировалась в новом положении.
Если мы используем обратимые вычисления, то отбираемая энергия передаётся следующему элементу в цепочке вычислений, но если наши вычисления необратимы, излишек энергии мы обязаны рассеять в окружающее пространство в виде далее не утилизируемой теплоты.
Будем исходить из того, что все приведённые выше рассуждения верны (у сообщества с 1961 года было достаточно времени проверить все теоретические выкладки), и, как следствие, для случая двухстабильной потенциальной ямы верна формула W = kB T ln2.
Для преодоления ограничения вместо двоичной системы кодирования данных применим четверичную. Соответственно изменится схема устройства:
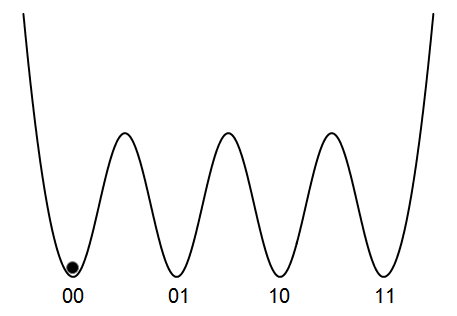
Мы по-прежнему для переключения состояния должны придать частице энергию для преодоления барьера и по-прежнему должны (в случае необратимого вычисления) излишек энергии рассеять в виде тепла. Только теперь энергия W расходуется не на один бит данных, а на два. Таким образом, при пересчёте на один бит формула теперь выглядит так:
Барьер Ландауэра оказался снижен ровно в два раза. Если в системе сделать не 4 потенциальных ямки, а 8, то величина необходимо рассеиваемой энергии станет W = kB T ln2 / 3. В предельном случае, когда количество потенциальных ямок устремляется к бесконечности (не представляю себе, как это может быть реализовано на практике, но в теории такое имеет право на существование) барьер Ландауэра устремляется к нулю.
До сих пор принцип Ландауэра рассматривался как непреодолимое фундаментальное ограничение, накладываемое на увеличение вычислительной мощности, но оказалось, что оно является следствием выбора варианта архитектуры вычислительной системы. А именно, раздельного кодирования битов данных элементами системы.
UPD (необходимое уточнение, спасибо Pshir): обратите пожалуйста внимание на вот эту цепочку комментариев: этот → этот → и вот этот.
То есть если вычисление производится при комнатной температуре (300K), то при потере 1 бита данных вычислительная система не может не рассеять в окружающее пространство примерно 2,7×10-21 Дж.
Считается, что единственный способ преодолеть это ограничение − использовать так называемые обратимые вычисления. В этой статье я докажу, что принцип Ландауэра не является догмой, и преодоление устанавливаемого им барьера возможно в том числе и без использования обратимых вычислений.
Откуда взялось ограничение
Ключ к пониманию того, из чего следует принцип Ландауэра − во фразе "A simple binary device consists of a particle in a bistable potential well" (простейшее двоичное устройство состоит из частицы в двухстабильной потенциальной яме):
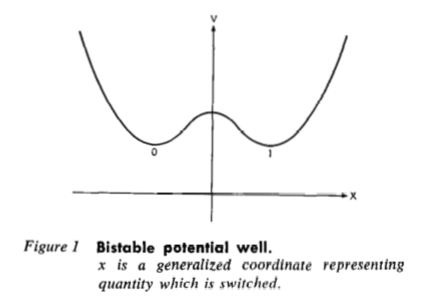
Для того, чтобы переключить систему с состояния «0» в состояние «1» (или наоборот), мы должны:
1. Придать частице энергию, достаточную для преодоления барьера.
2. Отобрать у частицы энергию для того, чтобы частица зафиксировалась в новом положении.
Если мы используем обратимые вычисления, то отбираемая энергия передаётся следующему элементу в цепочке вычислений, но если наши вычисления необратимы, излишек энергии мы обязаны рассеять в окружающее пространство в виде далее не утилизируемой теплоты.
Преодолеваем ограничение
Будем исходить из того, что все приведённые выше рассуждения верны (у сообщества с 1961 года было достаточно времени проверить все теоретические выкладки), и, как следствие, для случая двухстабильной потенциальной ямы верна формула W = kB T ln2.
Для преодоления ограничения вместо двоичной системы кодирования данных применим четверичную. Соответственно изменится схема устройства:

Мы по-прежнему для переключения состояния должны придать частице энергию для преодоления барьера и по-прежнему должны (в случае необратимого вычисления) излишек энергии рассеять в виде тепла. Только теперь энергия W расходуется не на один бит данных, а на два. Таким образом, при пересчёте на один бит формула теперь выглядит так:
W = kB T ln2 / 2
Барьер Ландауэра оказался снижен ровно в два раза. Если в системе сделать не 4 потенциальных ямки, а 8, то величина необходимо рассеиваемой энергии станет W = kB T ln2 / 3. В предельном случае, когда количество потенциальных ямок устремляется к бесконечности (не представляю себе, как это может быть реализовано на практике, но в теории такое имеет право на существование) барьер Ландауэра устремляется к нулю.
Вывод
До сих пор принцип Ландауэра рассматривался как непреодолимое фундаментальное ограничение, накладываемое на увеличение вычислительной мощности, но оказалось, что оно является следствием выбора варианта архитектуры вычислительной системы. А именно, раздельного кодирования битов данных элементами системы.
UPD (необходимое уточнение, спасибо Pshir): обратите пожалуйста внимание на вот эту цепочку комментариев: этот → этот → и вот этот.






