Прохождение Венеры по диску Солнца и определение расстояния между ними

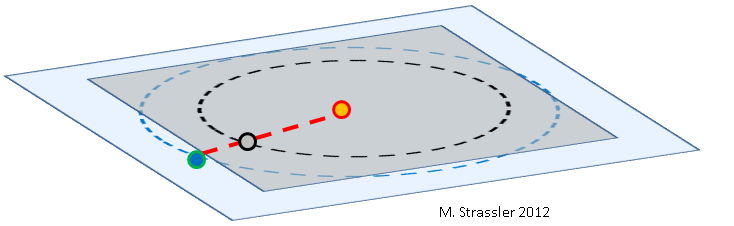
Рис. 1: Земля (синяя), Венера (серая) и Солнце (оранженвое), не в масштабе.

По поводу прохождения Венеры по диску Солнца 2012 года написано уже много статей. О том, как редко случается это событие, и почему именно: по идее, Венера, движущаяся вокруг Солнца чаще, чем Земля, должна проходить между Землёй и Солнцем во время каждого своего оборота (рис. 1), но из-за того, что орбиты двух планет не выровнены (не находятся в одной плоскости, см. рис. 2), Венера часто проходит выше или ниже Солнца с точки зрения Земли.

Но вместо того, чтобы повторять слова других, я хочу добавить несколько деталей, которые не так легко найти в интернете.

Вы, возможно, читали, что при помощи техники, основанной на рассуждениях астронома Эдмунда Галлея (известного кометой Галлея), сделанных им с 1678 по 1716 года, а также Джеймса Грегори до него, прохождение Венеры 1716 года был использован для определения расстояния от Земли до Солнца (и до Венеры, и всех остальных планет) с погрешностью в 2% — высочайшая из достигнутых на то время. Надеялись, что точность будет в 10 раз выше, но в процесс вмешался неожиданный оптический эффект под названием "эффект чёрной капли" — по поводу точных причин его возникновения до сих пор идут споры. Но вы могли не прочесть, что это измерение — и множество других измерений расстояний в астрономии, вплоть до достаточно близко расположенных звёзд — основано на принципе параллакса, на том же геометрическом факте, который используется нашими глазами и мозгом для восприятия глубины, или нашей способности чувствовать, насколько далеко от нас находятся объекты, просто взглянув на них.


Рис. 2: Земля (синяя), Венера (серая) и Солнце (оранжевое), не в масштабе. Орбита Венеры (чёрный круг в сером прямоугольнике) наклонена относительно орбиты Земли (синий круг в голубом прямоугольнике). Градус наклона сильно преувеличен. Поскольку Земля и Венера вращаются вокруг Солнца с разными скоростями, они могут проходить мимо друг друга в любых точках орбит.

Верх: большую часть при таком проходе Венера находится выше или ниже (зелёная линия) линии, соединяющей Землю и Солнце (красная линия), поэтому прохождения Венеры по диску Солнца не происходит.

Внизу: В редких случаях линия, соединяющая Землю и Солнце, совпадает с линией пересечения плоскостей орбит, и Венера находится вблизи этой же линии, что и ведёт к прохождению.

Без параллакса тоже несложно определить относительное расстояние от Венеры до Солнца — то есть, отношение радиуса орбиты Венеры L_V к радиусу орбиты Земли L_E. Поэтому в астрономии эпохи Возрождения довольно рано были высчитаны относительные расстояния от планет до Земли и Солнца. Но чтобы определить L_V и L_E отдельно, необходимо измерить параллакс, и прохождение Венеры может его обеспечить. Прохождение Венеры в 1760-х дало довольно точное измерение величины L_E — L_V, «абсолютного» расстояния от Земли до Венеры; это позволило узнать L_E, L_V, и расстояния до всех остальных планет с погрешностью в пару процентов. До этого, в конце XVII в, было сделано измерение расстояния от Земли до Марса, имевшее погрешность около 10%; оно тоже было основано на параллаксе, но это совсем другая история.

Предварительное замечание: Земля и Венера, и даже Солнце очень малы по сравнению с расстояниями между ними, поэтому нарисовать точные изображения практически невозможно. На иллюстрациях всё время приходится рисовать планеты большими, чем они есть на самом деле, по отношению к расстояниям между ними, просто чтобы вы смогли понять концепцию. Имейте это в виду! Все мои иллюстрации сделаны не в масштабе.

Относительные размеры орбит Венеры и Земли

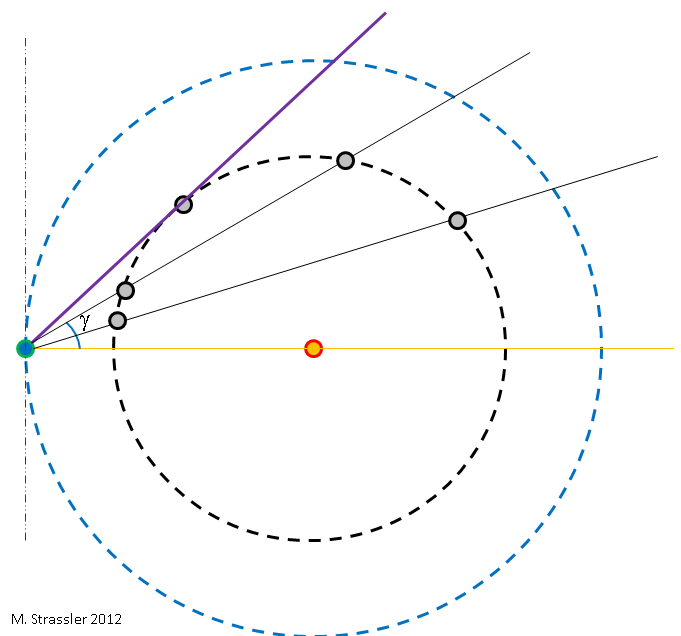
Рис. 3

Чтобы понять основную причину простоты определения L_V/L_E, предположим, что орбиты Земли и Венеры круговые и выровненные — они лежат в одной плоскости (как показано на рис. 1, изометрически, и на рис. 3 — вид «сверху»). На самом деле, орбиты Земли и Венеры немного вытянутые и не выровнены (рис. 2). Но эллиптичность и несовпадение плоскостей не сильно важны для наших рассуждений, поэтому сперва мы сможем их проигнорировать, а потом вновь вспомнить, чтобы получить более точные ответы.

Здесь мы применим классическую для физики технологию: сделаем приближение, достаточное для текущей задачи, и не будем углубляться больше, чем нужно. Это очень мощный способ размышления о науке и о знании вообще — на любой вопрос достаточно ответить с определённым уровнем точности, поэтому можно использовать простейшую технику из тех, что дадут вам нужный уровень точности. Этот метод прекрасно используется столетиями и применим не только к физике.

Поэтому мы примем приближение, по которому орбиты круговые и выровнены, и получим примерно правильные ответы, с погрешностью в несколько процентов. Этого будет достаточно для того, чтобы продемонстрировать основные концепции, чего я и добиваюсь. Поверьте мне, что можно сделать гораздо более точные вычисления — или же можете самостоятельно стать экспертом в этом вопросе. Но наше приближение не только даст очень неплохой ответ, но и сможет показать, почему так легко вычислить отношение L_V к L_E, но не сами значения L_V и L_E.

В течение года, когда Земля и Венера вращаются вокруг Солнца с разными скоростями, относительное положение Земли и Венеры по отношению к Солнцу меняется. Если в определённый день (день, месяц, год) я решу нарисовать картинку с Солнцем в центре и с Землёй слева, как на рис. 2, тогда Венера может оказаться в любом месте своей орбиты. Это значит, что с точки зрения Земли, угол между Венерой и Солнцем в небе будет меняться в зависимости от даты. Это показано на рис. 3, где угол назван γ. Угол легко измерить; найдите Венеру в небе после заката или перед восходом и измерьте угол между Венерой и Солнцем; см. рис. 4.


Рис. 4

Из рис. 3 видно, что у γ есть максимальный размер — угол между оранжевой и фиолетовой линиями. Перемещаясь по орбите, Венера с каждым закатом будет появляться в другом месте; некоторое время она будет несколько ночей подряд подниматься всё выше над горизонтом, а затем постепенно начнёт появляться ниже. Наблюдая за Венерой несколько ночей подряд и измеряя γ, мы можем определить максимальное значение γ, которое я назову γ_max.

Из рис. 3 очевидно, что (как показано на рис. 4) γ_max меньше 90°, поскольку фиолетовая линия должна лежать между оранжевой и красной, перпендикуляром. Геометрически это следствие того, что Венера всегда находится ближе к Солнцу, чем Земля. Эти углы объясняют, почему Венера всегда видна либо сразу после захода или перед рассветом (за исключением тех дней, когда она расположена за Солнцем). Венера не может быть в зените после наступления темноты, поскольку для этого ей надо было бы находиться слева от красной линии.


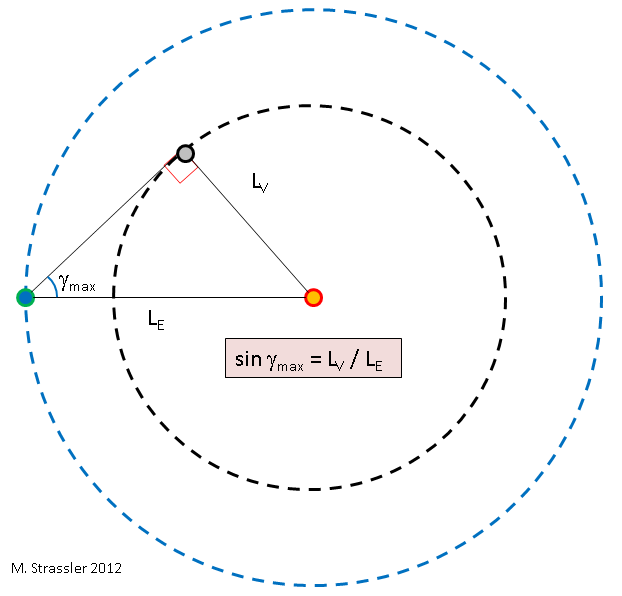
Рис. 5

Теперь мы можем определить отношение радиусов двух орбит — L_V к L_E — используя γ_max. Это простейшая геометрия, см. рис. 5. Суть в том, что когда Венера находится на максимальном угле от Солнца, линия между Солнцем и Венерой перпендикулярна линии между Землёй и Венерой, поэтому линии, соединяющие эти три объекта, образуют прямоугольный треугольник. Отсюда получаем при помощи стандартной тригонометрии:

И отсюда же, при помощи других простейших геометрических формул, мы получаем отношения между расстояниями до других планет.

Это не совсем точно, по причинам, указанным в начале; орбиты планет — эллипсы, и не лежат водной плоскости. Иначе говоря, L_V и L_E не сохраняются в течение года, а γ_max применяется немного сложнее, в трёх измерениях, как на рис. 2, а не в двух, как на рис. 1, 3 и 5. Но при помощи точных измерений положения Венеры и Солнца в небе возможно определить точные орбиты Венеры и Земли вокруг Солнца и улучшить расчёты. Смысл тот же; все измерения положения Венеры и Солнца в небе позволяют лишь измерить относительные размеры орбит Венеры и Земли. Но точные величины L_V и L_E так определить нельзя. Тут нужен другой подход.

Прохождение Венеры, параллакс и расстояние до Солнца

Причина, по которой прохождение Венеры позволяет измерить абсолютные величины орбит Земли и Венеры — этот процесс можно наблюдать с высокой точностью с разных мест земного шара, в результате чего у вас будут две перспективы видимого местонахождения Венеры по отношению к Солнцу, измеренные из разных мест с известным расстоянием между ними. Измерение параллакса позволяет определить абсолютную величину расстояние от Земли до Венеры из угла параллакса и расстояния между двумя точками измерения на Земле — точно так же, как разный вид объекта для левого и правого глаза позволяет нашему мозгу выдавать для нас ощущение глубины — чувство расстояния до объектов.


Рис. 6

Для демонстрации позвольте мне нарисовать то, как это будет выглядеть с крупной планеты. На рис. 6 показана планета, с которой мы будем наблюдать прохождение (это будет Земля) и проходящая перед звездой планета (это будет Венера). Я представлю упрощённую ситуацию (просто чтобы геометрия стала более простой и основную концепцию было проще увидеть), в которой планеты и звезда выровнены, поэтому с точки зрения наблюдателя на экваторе проходящая планета будет проходить по экватору звезды. Сверху на рис. 6 показан вид «сбоку»; обратите внимание на красную линию, идущую от экватора наблюдающей планеты к звезде через экватор планеты, проходящей по диску звезды.

В случае идеального выравнивания, наблюдатель на экваторе внешней планеты увидит, как внутренняя планета проходит по экватору звезды. Это показано в виде красной линии внизу рис. 6. Но наблюдатель с южного полюса внешней планеты увидит, как внутренняя планета проходит звезду по пути (фиолетовая линия) к северу от экватора звезды (в случае северного полюса всё будет наоборот). Если измерить угол α в небе между путями, по которым двигается проходящая планета, и знать радиус R наблюдающей планеты, мы сможем нарисовать прямоугольный треугольник, соединяющий проходящую планету, центр наблюдающей планеты и полюс наблюдающей планеты, с малым углом &alpha. Простая тригонометрия даст нам расстояние D между планетами во время прохождения, где

Рис. 7

То же верно для Земли, Венеры и Солнца, кроме того, что Земля и Венера так малы по сравнению с расстоянием между ними и Солнцем, что угол α окажется равным порядка 1/20°! (Это довольно малая величина, но вполне измеримая, хотя для точного измерения расстояния до Солнца, которое хотели получить астрономы XVIII века, потребовалось бы довольно сложное технически точное измерение величины небольшого угла). Такой маленький угол я не нарисую, поэтому придётся вам поверить мне на слово, что происходящее является доведённой до предела версией того, что я изобразил на рис. 6, с планетами и звездой (Солнцем) гораздо меньшими, чем нарисованы там, по отношению к расстояниям. Даже изображение на рис. 7 делает планеты гораздо больше, чем они есть. Но идея остаётся неизменной: расстояние D_EV между Землёй и Венерой во время прохождения можно определить, измерив угол параллакса α (внизу рис. 7; отметьте, что угловой диаметр Солнца равен порядка 1/2°).

Однако осталось ещё много вопросов:

• Я рассказал, как измерить D_EV, расстояние от Земли до Венеры во время прохождения. Но разве нашей целью было не измерить L_E и L_V, расстояние от Земли до Солнца и от Венеры до Солнца?
• Никто не отправлялся на южный полюс Земли, чтобы наблюдать прохождение Венеры в 1761 или 1769 году.
• Я предположил идеально выровненные орбиты Земли, Венеры и положение Солнца, такие, что из точки на экваторе Земли можно было бы видеть Венеру, двигающуюся по экватору Солнца. Но это на самом деле не так, и даже близко не похоже на типичное прохождение (и в 2012-м такого тоже не было).
• Угол α достаточно мал, чтобы его можно было точно измерить — особенно во времена до фотографии и мгновенных сообщений, в отсутствие чётких указаний на местоположение северного полюса Солнца, из-за чего сложно точно сравнить измерения пути Венеры, сделанные с двух разных точек Земли. Однако первичной целью было измерить угол не хуже, чем 1 часть из 500 (0,2%) (хотя из-за эффекта чёрной капли результат получился ближе к 1 части из 50 (2%)).

Как же справиться с этими проблемами?

Первое, как пройти от измерения D_EV до измерения нужных величин, L_E и L_V? Это просто — все взаимоотношения нам уже известны, в частности, мы уже знаем L_E/L_V (примерно, из рис. 4, или, если подойти к вопросу более тщательно, можно подсчитать и точнее) из максимального угла γ_max между Венерой и Солнцем с точки зрения Земли. Нам также известно D_EV = L_E — L_V = L_E (1 — L_V/L_E) из рис. 7. Поэтому мы можем получить приближённое значение L_E при помощи:

где α — угол параллакса, измеренный во время транзита, а γ_max — максимальный угол между Венерой и Солнцем (рис. 5). Более точные измерения требуют более сложной геометрии, однако с той же основной идеей.

Второе, даже если бы орбиты планет были идеально выровнены, два измерения пути Венеры не нужно измерять с экватора и полюса Земли. Их можно измерить с двух любых широт. Геометрия становится немного сложнее, но не сильно, а принцип остаётся (см. рис. 8).


Рис. 8

Третье, даже без идеального выравнивания появится небольшой угол параллакса при измерении величин с двух разных точек Земли, и если хорошо измерить этот угол, это измерение можно превратить (через чуть более сложные уравнения) в измерение D. Это показано на рис. 8, внизу.

Четвёртый вопрос — исторически сложная проблема измерения углового сдвига пути Венеры во время прохождения на угол α ведёт нас к альтернативной попытке измерения времени — либо времени прохождения, либо просто начала и конца прохождения, а не углов. Первый вариант был предложен Галлеем на основе идей Грегори, а второй, в качестве дальнейшего улучшения, предложил Жозеф Никола Делиль. Метод Галлея не требовал синхронизации часов в разных местах Земли; метод Делиля требовал, поэтому основывался на более передовой часовой технологии.

Даже в XVII или XVIII веке гораздо проще выполнить точное измерение интервала, или моментов начала и завершения затмения, чем точно измерить местоположение Венеры относительно диска Солнца, особенно при отсутствии фотографии. На рис. 9 можно видеть, что фиолетовый и красный пути Венеры, пересекающей Солнце, имеют немного отличные длины из-за того, что они не пересекают его в одном месте, а это значит, что длительность прохождения будет отличаться на время, связанное с углом параллакса. К сожалению, всё оказывается сложнее, чем выглядит на первый взгляд — Земля вертится и движется вокруг Солнца, поэтому наблюдатель проходит довольно значительное расстояние во время прохождения Венеры по диску Солнца. Поэтому требуется много усилий (вычисления довольно сложны, хотя с современными компьютерами они гораздо проще) для определения разницы временных интервалов начала и конца прохождения, наблюдаемого двумя разными наблюдателями на Земле, в зависимости от расстояния до Солнца.

Галлей в начале XVIII века понимал все необходимые геометрические принципы (если вычесть устаревшую английскую фразеологию и стиль из его текстов, вы будете удивлены, как современно звучат его сложные утверждения, и вы увидите, что учёные ещё триста лет назад были очень похожи на сегодняшних учёных, обладали таким же интеллектом и им не хватало только научной технологии сегодняшнего дня).


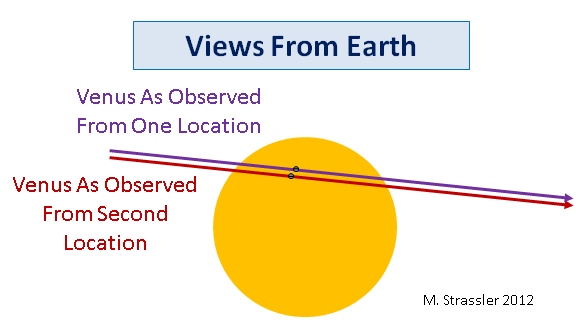
Рис. 9

Всё это говорит о том, что параллакс — различие в видимом положении, приписываемом Венере по отношению к Солнцу с точки зрения наблюдателей, измеряющих его в одно и то же время но с разных мест на Земле — исторически был очень важным методом, с помощью которого был определён размер Солнечной системы. Сегодня нам доступны и более мощные методы, но вам может быть интересным тот факт, что то, что вы видите сегодня в небе, имеет величайшую историческую важность, или же вы просто можете наслаждаться видом Венеры, величаво движущейся вокруг нашей звезды.