vlsergey 19 ноя 2019 в 18:13

Асимметричные криптографические протоколы распределения ключей: Деннинга—Сакко, DASS, Ву-Лама

4 мин

4.7K

Информационная безопасность*Криптография*

Предисловие

Данный текст будет являться одной из переписанных глав для учебного пособия по защите информации кафедры радиотехники и систем управления, а также, с этого учебного кода, кафедры защиты информации МФТИ (ГУ). Полностью учебник доступен на github (см. также draft releases). На Хабре планирую выкладывать новые «большие» куски, во-первых, чтобы собрать полезные комментарии и замечания, во-вторых, дать сообществу больше обзорного материала по полезным и интересным темам. Предыдущие разделы главы «Криптографически протоколы»: 1, 2, 3, 4, 5; следующий по порядку: 7.

Асимметричные протоколы, или же протоколы, основанные на криптосистемах с открытыми ключами, позволяют ослабить требования к предварительному этапу протоколов. Вместо общего секретного ключа, который должны иметь две стороны (либо каждая из сторон и доверенный центр), в рассматриваемых ниже протоколах стороны должны предварительно обменяться открытыми ключами (между собой либо с доверенным центром). Такой предварительный обмен может проходить по открытому каналу связи, в предположении, что криптоаналитик не может повлиять на содержимое канала связи на данном этапе.

Протокол Деннинга—Сакко

Протокол предложен Дороти Деннинг и Джованни Сакко в 1981 году (англ. Dorothy E. Denning, Giovanni Maria Sacco). В данном протоколе к доверенному центру (Тренту) за сертификатами сразу обоих участников обращается инициатор (Алиса). Этот же участник отвечает и за формирование нового сессионного ключа $inline$ .

Взаимодействие участников в протоколе Деннинга—Сакко

$Alice \to \left\{ A, B \right\} \to Trent$
$Trent \to \left\{ S_T( A, K_A, T_T ), S_T( B, K_B, T_T ) \right\} \to Alice$
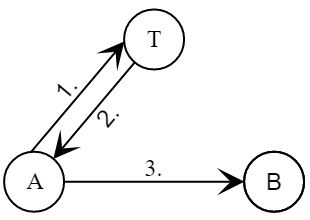
Алиса генерирует новый сессионный ключ $inline$
$\begin{array}{lll} Alice \to \{ & E_B( S_A ( K, T_A ) ), & \\ & S_T( A, K_A, T_T ), & \\ & S_T( B, K_B, T_T ) & \} \to Bob \end{array}$
Боб проверяет подпись доверенного центра на сертификате $inline$ , расшифровывает сессионный ключ $inline$ и проверяет подпись Алисы.

Отсутствие в сообщении $inline$ каких-либо идентификаторов делает протокол уязвимым к атаке с известными сеансовым ключом и позволяет второй стороне (Бобу) выдать себя за инициатора (Алису) в сеансе с третьей стороной (Кларой).

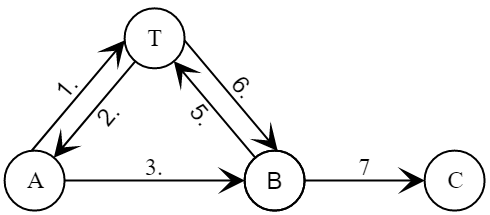
Алиса и Боб провели сеанс протокола, выработав новый сессионный ключ $inline$ .
$Bob \to \left\{ B, C \right\} \to Trent$
$Trent \to \left\{ S_T( B, K_B, T_T ), S_T( C, K_C, T_T ) \right\} \to Bob$
Боб воспроизводит сообщения $inline$ и $inline$ от Алисы в сеансе с Кларой:
$\begin{array}{lll} Bob~(Alice) \to \{ & E_C( S_A ( K, T_A ) ), & \\ & S_T( A, K_A, T_T ), & \\ & S_T( C, K_C, T_T ) & \} \to Clara \end{array}$
Клара успешно проверяет подпись доверенного центра на сертификате $inline$ , расшифровывает сессионный ключ $inline$ и проверяет подпись Алисы.

В результате Клара уверена, что получила от Алисы новый сессионный ключ $inline$ .

Протокол DASS

Протокол DASS являлся составной частью сервиса распределённой аутентификации DASS (англ. Distributed Authentication Security Service), разработанного компанией DEC и описанного в RFC 1507 в сентябре 1993 года.

В протоколе DASS, по аналогии с протоколами Wide-Mouth Frog и Деннинга—Сакко, инициатор (Алиса) генерирует и новый сеансовый ключ, и, для каждого сеанса протокола, новую пару открытого и закрытого ключей отправителя. Доверенный центр (Трент) используется как хранилище сертификатов открытых ключей участников. Но в отличие от Деннинга—Сакко к доверенному центру обращаются по очереди оба участника.

Взаимодействие участников в протоколе DASS

$Alice \to \left\{ B \right\} \to Trent$
$Trent \to \left\{ S_T \left( B, K_B \right) \right\} \to Alice$
$Alice \to \left\{ E_K \left( T_A \right), S_A \left( L, A, K_P \right), S_{K_P} \left( E_B \left( K \right) \right) \right\} \to Bob$
$Bob \to \left\{ A \right\} \to Trent$
$Trent \to \left\{ S_T \left( A, K_A \right) \right\} \to Bob$
$Bob \to \left\{ E_K \left\{ T_B \right\} \right\} \to Alice$

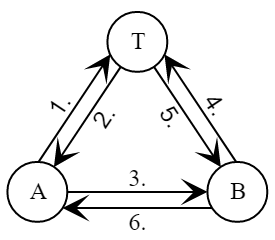
С помощью сертификатов открытых ключей $\left\{ S_T \left( B, K_B \right) \right\}$ и $\left\{ S_T \left( A, K_A \right) \right\}$ , которые отправляет Трент, и дальнейшего подтверждения владения соответствующими ключами, участники могут аутентифицировать друг-друга. Успешная расшифровка временных меток из сообщений $E_K \left( T_A \right)$ и $E_K \left\{ T_B \right\}$ обеспечивает подтверждение владением сеансовым ключом.

В протоколе используется время жизни ( $inline$ ) сеансового ключа $inline$ , однако в сообщение не включена метка времени. В результате протокол остаётся уязвимым к атаке с известным сеансовым ключом. Предположим, что Меллори смогла записать полностью прошедший сеанс связи между Алисой и Бобом, а потом смогла получить доступ к сеансовому ключу $inline$ . Это позволяет Меллори аутентифицировать себя как Алиса перед Бобом.

$Mellory~(Alice) \to \left\{ E_K \left( T_M \right), S_A \left( L, A, K_P \right), S_{K_P} \left( E_B \left( K \right) \right) \right\} \to Bob$
$Bob \to \left\{ A \right\} \to Trent$
$Trent \to \left\{ S_T \left( A, K_A \right) \right\} \to Bob$
$Bob \to \left\{ E_K \left\{ T_B \right\} \right\} \to Alice$

На первом проходе Меллори меняет только первое сообщение, содержащее метку времени $E_K \left( T_M \right)$ . Всё остальное Меллори копирует из записанного сеанса связи. Если Боб не записывает используемые ключи, он не заметит подмены. Простейшее исправление данной уязвимости состоит во включении метки времени в сообщение $S_A \left( T_A, L, A, K_P \right)$ .

Так как в протоколе сеансовый ключ $inline$ шифруется «мастер»-ключом Боба $inline$ , то компрометация последнего приведёт к компрметации всех использованных ранее сеансовых ключей. То есть протокол не обеспечивает совершенной прямой секретности (цель G9).

Ни Трент, ни Боб не участвуют в формировании новых сеансовых ключей. Поэтому Алиса может заставить Боба использовать старый сеансовый ключ, как в протоколах Wide-Mouth Frog и Yahalom.

Протокол Ву—Лама

Протокол Ву—Лама, предложенный в 1992 году (англ. Thomas Y. C. Woo, Simon S. Lam), добавляет к сообщениям случайные числа участников, что позволяет защитить протокол в том числе от атак повтором, а также обеспечивает подтверждение владения ключами. Также это единственный из рассмотренных в этом разделе протоколов, в котором новый ключ формируется доверенной стороной (Трентом).

Взаимодействие участников в протоколе Ву—Лама

$Alice \to \left\{ A, B \right\} \to Trent$
$Trent \to \left\{ S_T( K_B ) \right\} \to Alice$
$Alice \to \left\{ E_B ( A, R_A ) \right\} \to Bob$
$Bob \to \left\{ A, B, E_T( R_A ) \right\} \to Trent$
$Trent \to \left\{ S_T( K_A ), E_B ( S_T ( R_A, K, A, B ) ) \right\} \to Bob$
$Bob \to \left\{ E_A (S_T (R_A, K, A, B), R_B) \right\} \to Alice$
$Alice \to \left\{ E_K( R_B ) \right\} \to Bob$

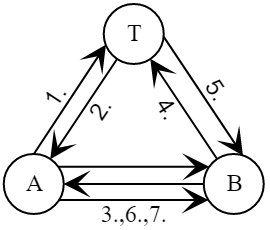
Так как в сертификате сессионного ключа $inline$ присутствует случайное число Алисы $inline$ , то злоумышленник не сможет использовать старый сертификат в новом сеансе от имени Боба. Следовательно 6-й проход протокола позволяет Алисе убедиться, что Боб знает новый сессионный ключ $inline$ , и, следовательно владеет своим «мастер»-ключом $inline$ (так как это единственный способ получить сертификат из сообщения $inline$ ).

Сообщение $inline$ от Алисы к Бобу на седьмом проходе позволяет одновременно гарантировать, что Алиса знает и свой «мастер»-ключ $inline$ (так как смогла расшифровать $E_A(\dots, R_B)$ ), и новый сессионный ключ $inline$ , так как смогла корректно зашифровать $inline$ этим ключом.

Послесловие

Последним разделом главы про распределение ключей является уже опубликованный материал о квантовом протоколе BB84. Так что текущая статья фактически завершает цикл разделов про криптографические протоколы для Хабра. Автор будет благодарен за фактические и другие замечания к тексту.

Теги:

Хабы:

Асимметричные криптографические протоколы распределения ключей: Деннинга—Сакко, DASS, Ву-Лама

Протокол Деннинга—Сакко

Протокол DASS

Протокол Ву—Лама

Публикации

Работа

Ближайшие события