worker_sam 22 дек 2019 в 22:29

Использование сверточной нейронной сети для игры в «Жизнь» (на Keras)

10 мин

11K

Цель этой статьи — научить нейронную сеть играть в игру "Жизнь", не обучая ее правилам игры.

Привет, Хабр! Представляю вашему вниманию перевод статьи "Using a Convolutional Neural Network to Play Conway's Game of Life with Keras" автора kylewbanks.

Если вы не знакомы с игрой под названием Жизнь (это клеточный автомат, придуманный английским математиком Джоном Конвеем в 1970 году), правила таковы.

Вселенная игры представляет собой бесконечную, двумерную сетку квадратных ячеек, каждая из которых находится в одном из двух возможных состояний: живая или мертвая (или населенная и незаселенная, соответственно). Каждая ячейка взаимодействует со своими восемью соседями по горизонтали, вертикали или диагонали. На каждом шаге во времени происходят следующие переходы:

Любая живая клетка с менее чем двумя живыми соседями умирает.
Любая живая клетка с двумя или тремя живыми соседями доживает до следующего поколения.
Любая живая клетка с более чем тремя живыми соседями умирает.
Любая мертвая клетка с ровно тремя живыми соседями становится живой клеткой.

Первое поколение создается путем применения вышеуказанных правил одновременно к каждой ячейке в начальном состоянии, рождения и смерти происходят одновременно в дискретные моменты времени. Каждое поколение — это чистая функция предыдущего. Правила продолжают применяться к новому поколению, чтобы создать следующие поколения.

Подробнее см. Википедию.

Зачем это делать? Главным образом для развлечения, и чтобы немного узнать о сверточных нейронных сетях.

Итак...

Игровая логика

Первое, что нужно сделать — это определить функцию, которая принимает игровое поле в качестве входных данных и возвращает следующее состояние.

К счастью, в Интернете доступно множество реализаций, таких как: https://jakevdp.github.io/blog/2013/08/07/conways-game-of-life/.

По сути, он принимает матрицу игрового поля в качестве входных данных, где 0 представляет мертвую ячейку, а 1 представляет живую ячейку и возвращает матрицу того же размера, но содержащую состояние каждой ячейки на следующей итерации игры.

import numpy as np

def life_step(X):
    live_neighbors = sum(np.roll(np.roll(X, i, 0), j, 1)
                     for i in (-1, 0, 1) for j in (-1, 0, 1)
                     if (i != 0 or j != 0))
    return (live_neighbors == 3) | (X & (live_neighbors == 2)).astype(int)

Генерация игрового поля

Следуя игровой логике, нам понадобится способ произвольно генерировать игровые поля и способ их визуализации.

Функция generate_frames создает num_frames случайных игровых полей с определенной формой и предопределенной вероятностью того, что каждая ячейка будет "живой", а render_frames рисует представления изображений двух игровых полей рядом для сравнения (живые ячейки белые, а мертвые ячейки черные):

import matplotlib.pyplot as plt

def generate_frames(num_frames, board_shape=(100,100), prob_alive=0.15):
    return np.array([
        np.random.choice([False, True], size=board_shape, p=[1-prob_alive, prob_alive])
        for _ in range(num_frames)
    ]).astype(int)

def render_frames(frame1, frame2):
    plt.subplot(1, 2, 1)
    plt.imshow(frame1.flatten().reshape(board_shape), cmap='gray')

    plt.subplot(1, 2, 2)
    plt.imshow(frame2.flatten().reshape(board_shape), cmap='gray')

Давайте посмотрим, как выглядят эти поля:

board_shape = (20, 20)
board_size = board_shape[0] * board_shape[1]
probability_alive = 0.15

frames = generate_frames(10, board_shape=board_shape, prob_alive=probability_alive)
print(frames.shape) # (num_frames, board_w, board_h)

(10, 20, 20)

print(frames[0])

[[0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0],
 [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
 [0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1],
 [1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
 [1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0],
 [0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0],
 [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
 [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0]])

Далее берется целочисленное представление игрового поля и отображается, как изображение.
Справа также показано следующее состояние игрового поля с помощью функции life_step:

ender_frames(frames[1], life_step(frames[1]))

Построение обучающего и тестового наборов

Теперь мы можем сгенерировать данные для обучения, проверки и тестирования.

Каждый элемент в массивах y_train/y_val/y_test будет представлять следующее поле игры для каждого кадра поля в X_train/X_val/X_test.

def reshape_input(X):
    return X.reshape(X.shape[0], X.shape[1], X.shape[2], 1)

def generate_dataset(num_frames, board_shape, prob_alive):
    X = generate_frames(num_frames, board_shape=board_shape, prob_alive=prob_alive)
    X = reshape_input(X)
    y = np.array([
        life_step(frame) 
        for frame in X
    ])
    return X, y

train_size = 70000
val_size   = 10000
test_size  = 20000

print("Training Set:")
X_train, y_train = generate_dataset(train_size, board_shape, probability_alive)
print(X_train.shape)
print(y_train.shape)

Training Set:
(70000, 20, 20, 1)
(70000, 20, 20, 1)

print("Validation Set:")
X_val, y_val = generate_dataset(val_size, board_shape, probability_alive)
print(X_val.shape)
print(y_val.shape)

Validation Set:
(10000, 20, 20, 1)
(10000, 20, 20, 1)

print("Test Set:")
X_test, y_test = generate_dataset(test_size, board_shape, probability_alive)
print(X_test.shape)
print(y_test.shape)

Test Set:
(20000, 20, 20, 1)
(20000, 20, 20, 1)

Построение сверточной нейронной сети

Теперь мы можем сделать первый шаг к построению сверточной нейронной сети с использованием Keras. Ключевым моментом здесь являются размер ядра (3, 3) и шаг 1. Они указывают CNN использовать матрицу 3x3 окружающих ячеек для каждой ячейки поля, на которую она смотрит, включая текущую ячейку.

Например, если бы нижеследующее было игровым полем, а мы были в средней ячейке x, она бы посмотрела на все ячейки, отмеченные восклицательным знаком ! и ячейку х. Затем сеть двигается вдоль ячейки вправо и делает то же самое, повторяя снова и снова, пока не обработает каждую ячейку и ее соседей по всему полю.

Остальная сеть довольно проста, поэтому я не буду вдаваться в подробности. Если вам что-нибудь интересно, я рекомендую почитать документацию.

from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Conv2D, MaxPool2D

# CNN Properties
filters = 50
kernel_size = (3, 3) # look at all 8 neighboring cells, plus itself
strides = 1
hidden_dims = 100

model = Sequential()
model.add(Conv2D(
    filters, 
    kernel_size,
    padding='same',
    activation='relu',
    strides=strides,
    input_shape=(board_shape[0], board_shape[1], 1)
))
model.add(Dense(hidden_dims))
model.add(Dense(1))
model.add(Activation('sigmoid'))

model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

Взглянем на вывод функции summary:

model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_9 (Conv2D)            (None, 20, 20, 50)        500       
_________________________________________________________________
dense_17 (Dense)             (None, 20, 20, 100)       5100      
_________________________________________________________________
dense_18 (Dense)             (None, 20, 20, 1)         101       
_________________________________________________________________
activation_9 (Activation)    (None, 20, 20, 1)         0         
=================================================================
Total params: 5,701
Trainable params: 5,701
Non-trainable params: 0
_________________________________________________________________

Обучение и сохранение модели

Построив CNN, давайте обучим модель и сохраним ее на диск:

def train(model, X_train, y_train, X_val, y_val, batch_size=50, epochs=2, filename_suffix=''):
    model.fit(
        X_train, y_train, 
        batch_size=batch_size, 
        epochs=epochs,
        validation_data=(X_val, y_val)
    )

    with open('cgol_cnn{}.json'.format(filename_suffix), 'w') as file:
        file.write(model.to_json())
    model.save_weights('cgol_cnn{}.h5'.format(filename_suffix))

train(model, X_train, y_train, X_val, y_val, filename_suffix='_basic')

Train on 70000 samples, validate on 10000 samples
Epoch 1/2
70000/70000 [==============================] - 27s 388us/step 
    - loss: 0.1324 - acc: 0.9651 - val_loss: 0.0833 - val_acc: 0.9815
Epoch 2/2
70000/70000 [==============================] - 27s 383us/step 
    - loss: 0.0819 - acc: 0.9817 - val_loss: 0.0823 - val_acc: 0.9816

Эта модель обеспечивает точность чуть более 98% как для тренировочных, так и для проверочных наборов, что очень хорошо для первого прохода. Давайте попробуем выяснить, где мы делаем ошибки.

Пробуем

Давайте посмотрим на прогноз для случайного игрового поля и на то, как он работает. Сначала создайте одно игровое поле и посмотрите на правильный следующий кадр:

X, y = generate_dataset(1, board_shape=board_shape, prob_alive=probability_alive)

render_frames(X[0].flatten().reshape(board_shape), y)

Далее, давайте выполним предсказание и посмотрим, сколько ячеек было неправильно предсказано:

pred = model.predict_classes(X)
print(np.count_nonzero(pred.flatten() - y.flatten()), "incorrect cells.")

4 incorrect cells.

Далее, давайте сравним правильный следующий шаг с предсказанным шагом:

render_frames(y, pred.flatten().reshape(board_shape))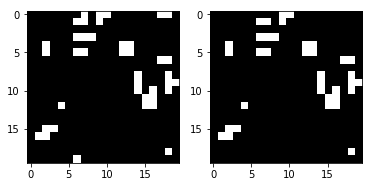

Это не страшно, но вы видите, где предсказание не удалось? Кажется, что сеть не может предсказать клетки по краям игрового поля. Посмотрим туда, где ненулевые значения указывают на неправильные предсказания:

print(pred.flatten().reshape(board_shape) - y.flatten().reshape(board_shape))

[[ 0  0  0  0  0  0  0 -1  0  0  0  0  0  0  0  0  0 -1 -1  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0 -1  0  0  0  0  0  0  0  0  0  0  0  0  0]]

Как видите, все ненулевые значения расположены по краям игрового поля. Давайте посмотрим на полный тестовый набор и подтвердим, что это наблюдение верно.

Просмотр ошибок, используя тестовый набор

Мы напишем функцию, которая отображает тепловую карту, показывающую, где модель делает ошибки, и вызовем ее, используя весь тестовый набор:

def view_prediction_errors(model, X, y):
    y_pred = model.predict_classes(X)
    sum_y_pred = np.sum(y_pred, axis=0).flatten().reshape(board_shape)
    sum_y = np.sum(y, axis=0).flatten().reshape(board_shape)

    plt.imshow(sum_y_pred - sum_y, cmap='hot', interpolation='nearest')
    plt.show()

view_prediction_errors(model, X_test, y_test)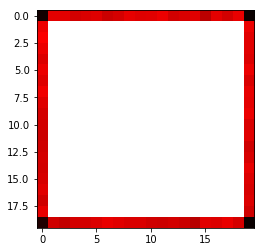

Все ошибки на краях и в углах. Что логично, так как CNN не может смотреть по сторонам, но логика игры в life_step это делает. Например, рассмотрим следующее. Глядя на краевую ячейку x ниже, CNN видит только x и ! клетки:

Но что мы действительно хотим, и что делает life_step, так это посмотреть на ячейки с противоположной стороны:

Похожая ситуация в углах:

Чтобы это исправить, Conv2D должен как-то смотреть на противоположную сторону игрового поля. В качестве альтернативы, каждая входное поле может быть предварительно обработано для заполнения краев с противоположной стороны, и тогда Conv2D может просто удалить первый или последний столбец и строку. Так как мы находимся во власти Keras и предоставляемых им функциональных возможностей заполнения, которые не поддерживают то, что мы ищем, нам придется прибегнуть к добавлению нашего собственного заполнения.

Исправление краевых дефектов с помощью заполнения

Нам нужно дополнить каждую игровое поле противоположным значением, чтобы имитировать то, как life_step работает для краевых значений. Мы можем использовать np.pad с mode = ’wrap’ для этого. Например, рассмотрим следующий массив и дополненный вывод ниже:

x = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
])

print(np.pad(x, (1, 1), mode='wrap'))

[[9, 7, 8, 9, 7],
 [3, 1, 2, 3, 1],
 [6, 4, 5, 6, 4],
 [9, 7, 8, 9, 7],
 [3, 1, 2, 3, 1]]

Обратите внимание, что первый столбец/строка и последний столбец/строка отзеркаливают противоположную сторону исходной матрицы, а средняя матрица 3x3 является исходным значением x. Например, ячейка [1] [1] была скопирована на противоположной стороне в ячейке [4] [1], и аналогично [0] [1] содержит [3] [1]. Во всех направлениях и даже в углах массив был исправлен так, чтобы он содержал противоположную сторону. Это позволит CNN рассмотреть все игровое поле и правильно обработать крайние случаи.

Теперь мы можем написать функцию для заполнения всех наших входных матриц:

def pad_input(X):
    return reshape_input(np.array([
        np.pad(x.reshape(board_shape), (1,1), mode='wrap')
        for x in X
    ]))

X_train_padded = pad_input(X_train)
X_val_padded = pad_input(X_val)
X_test_padded = pad_input(X_test)

print(X_train_padded.shape)
print(X_val_padded.shape)
print(X_test_padded.shape)

(70000, 22, 22, 1)
(10000, 22, 22, 1)
(20000, 22, 22, 1)

Все наборы данных теперь дополнены обернутыми столбцами/строками, что позволяет CNN видеть противоположную сторону игрового поля, как это делает life_step. Из-за этого каждое игровое поле теперь имеет размер 22x22 вместо оригинальных 20x20.

Затем, CNN должен быть перестроен так, чтобы отбрасывать заполнение, используя padding = 'valid' (что говорит Conv2D отбрасывать края, хотя это не сразу очевидно), и обработки нового input_shape. Таким образом, когда мы пропускаем игровые поля с размером 22x22, мы по-прежнему получаем размер 20x20 в качестве выходного, поскольку отбрасываем первый и последний столбец/строку. Остальное остается идентичным:

model_padded = Sequential()
model_padded.add(Conv2D(
    filters, 
    kernel_size,
    padding='valid',
    activation='relu',
    strides=strides,
    input_shape=(board_shape[0] + 2, board_shape[1] + 2, 1)
))
model_padded.add(Dense(hidden_dims))
model_padded.add(Dense(1))
model_padded.add(Activation('sigmoid'))

model_padded.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model_padded.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_10 (Conv2D)           (None, 20, 20, 50)        500       
_________________________________________________________________
dense_19 (Dense)             (None, 20, 20, 100)       5100      
_________________________________________________________________
dense_20 (Dense)             (None, 20, 20, 1)         101       
_________________________________________________________________
activation_10 (Activation)   (None, 20, 20, 1)         0         
=================================================================
Total params: 5,701
Trainable params: 5,701
Non-trainable params: 0
_________________________________________________________________

Теперь мы можем обучиться, используя выровненное поле:

train(
    model_padded, 
    X_train_padded, y_train, X_val_padded, y_val, 
    filename_suffix='_padded'
)

Train on 70000 samples, validate on 10000 samples
Epoch 1/2
70000/70000 [==============================] - 27s 389us/step - loss: 0.0604 - acc: 0.9807 - val_loss: 4.5475e-04 - val_acc: 1.0000
Epoch 2/2
70000/70000 [==============================] - 27s 382us/step - loss: 1.7058e-04 - acc: 1.0000 - val_loss: 5.9932e-05 - val_acc: 1.0000

Точность предсказания составляет от 98% до 100%, которые мы получили до добавления отступов. Давайте посмотрим на ошибку на тестовом наборе:

view_prediction_errors(model_padded, X_test_padded, y_test)

Отлично! Черная тепловая карта указывает на то, что нет различий в значениях, и это означает, что мы успешно предсказали каждую ячейку для каждой игры.

Это было забавное маленькое упражнение, чтобы поиграть с сверточными нейронными сетями, не используя большого набора данных. Не стесняйтесь заглянуть на GitHub.

Теги:

Хабы:

Машинное обучение

Использование сверточной нейронной сети для игры в «Жизнь» (на Keras)

Игровая логика

Генерация игрового поля

Построение обучающего и тестового наборов

Построение сверточной нейронной сети

Обучение и сохранение модели

Пробуем

Просмотр ошибок, используя тестовый набор

Исправление краевых дефектов с помощью заполнения

Публикации

Истории

Работа

Ближайшие события