На досуге мы с сыном изучаем цифровую электронику. Недавно мы дошли до главы про конечные автоматы. На эту тему полно типичных задач, вроде семафора или торгового автомата. Но они все унылые и слишком простые, а некоторые вообще, честно скажем, притянуты за уши. После изучения простых примеров захотелось сделать что-то более интересное и сложное. На глаза попала классическая игра «змейка» (сын играл в неё на телефоне), и я предложил сделать её на конечных автоматах. Ведь состояние игры вполне конечное (особенно, если ограничиться небольшим полем), а из входов только 4 кнопки. И вот что у нас получилось.

Игра Snake (она же змейка, питон, удав и т.д.) широко всем известна. Родом она из далёких 70-х, но я не буду повторять её историю, которую вы можете почитать в википедии или множестве статей на Хабре. Игра имеет достаточно простые правила и при этом затягивающий геймплей )) Благодаря этому её часто используют для туториалов или примеров кода. На языках программирования высокого уровня сделать такую игру достаточно легко. Но вот в более ограниченных условиях начинается самое интересное, например реализация на LabVIEW. Есть также множество вариантов на FPGA: ссылка 1, ссылка 2, ссылка 3, ссылка 4. Но ещё не было ни одного варианта на отдельных ТТЛ-микросхемах стандартных серий. Значит этим мы и займёмся.
Казалось бы, самыми близкими для нас являются решения на FPGA и оттуда можно много позаимствовать? Но во всех вариантах, которые я посмотрел, с лёгкостью разбрасываются регистрами налево и направо. Например, очень часто выделяют для каждой клетки поля отдельный бит или число. С рассыпухой мы так поступить не можем, ведь каждый новый регистр — это отдельная микросхема, которую надо где-то разместить, а потом ещё и соединить. Поэтому мы перечеркнём весь накопленный другими разработчиками опыт и будем делать всё с нуля. В качестве бонуса будем собирать всё на отечественных (а лучше — советских) микросхемах серии к555/кр1533, за исключением ПЗУ, которые придётся взять свежие.
У нас будут такие ограничения: поле размером 8×8 клеток (китайская светодиодная матрица), длина хвоста 8 клеток. Змейка может проходить через стены, а пересечение с хвостом мы поначалу обрабатывать не будем (дабы не усложнять конструкцию, добавить это можно потом). Чтобы описать всё состояние игры нам понадобится:
Итого получается 65 бит, даже если брать регистры по 8 бит каждый, то только на хранение состояния понадобится 8 таких микросхем (и ещё один триггер), это довольно много.
Но хвост не может располагаться где ему вздумается, он «растёт» от головы. Поэтому мы можем хранить не полные координаты каждой секции хвоста, а только направление в какую сторону от предыдущей клетки (или головы) его надо нарисовать. Тогда вместо 6×8=48 бит нам понадобится 4×8=16 бит, а это уже экономия целых четырёх корпусов регистров!
Попробуем сделать всё на автоматах, похожих на автоматы Мура или Мили. Для реализации такого автомата достаточно иметь немного памяти состояний (регистр) и комбинационную логику для перехода между ними.
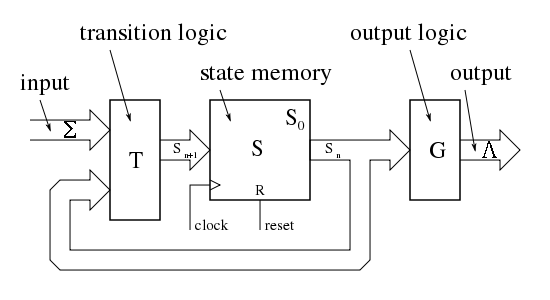
Картинка из википедии
Обычно конечный автомат описывают в виде графа состояний и переходов между ними. Иногда удобнее составить таблицу переходов в новое состояние, простейший пример (из википедии):

Больше информации и красивых картинок вы можете найти, например, в этой статье на Хабре
У змейки различных состояний (если не учитывать положения яблока) может быть 2^8+2^10+...+2^24 ≈ 32 миллиона. Расписать их в таблице, а уж тем более нарисовать граф переходов не представляется возможным. Но бóльшая часть переходов вполне однотипные (голова передвигается только на одну соседнюю клетку, а хвост продвигается по одной секции за ход). В таком случае мы можем описывать не каждое отдельное состояние, а сформулировать новое состояние в виде функции от предыдущего. Более того, всю игру мы можем разбить на несколько параллельных автоматов: 1) автомат направления, 2) автомат положения головы, 3) автомат для хвоста. И задать каждый из них так, как будет удобнее:
Начнём с автомата направления. Если хорошо подумать, то можно собрать его на отдельной логике. Но, поскольку задача в целом и так немаленькая, я решил, что проще будет сделать lookup table из EEPROM, а таблицу переходов записать вручную. Она будет иметь 6 входов, а значит только 64 значения, которые мы можем просто вбить в hex-редактор.

Для автомата положения головы написать такую таблицу будет намного сложнее. Но она содержит по сути только 2 операции: +1 и -1. Их можно реализовать на 4-х разрядном сумматоре К155ИМ6. Для +1 мы будем складывать нашу координату с b'0001, а для -1 с b'1111 (что собственно и есть -1 в дополненительном коде). Нам понадобятся два сумматора (для x и y), немного логики, а хранить состояние мы будем в 8-битном регистре ИР27 (их нам пригодится ещё много):

Соберём это на плате, а для проверки сразу подключим светодиодную матрицу с двумя дешифраторами. Дешифратор с инверсными выходами — ИД7, а для прямого можно было бы взять К561ИД1 (CD4028), но у меня под рукой его не было. Другой вариант — взять 8 транзисторов в качестве ключей, но делать этого не хотелось, поэтому пришлось бездарно потратить ещё один EEPROM (записав туда всего лишь 8 ячеек).

Логика нового положения головы на отдельной плате сверху
Ещё одно отступление
Сделаем небольшую передышку и сэкономим макетную плату (и несколько корпусов микросхем). Мы снова воспользуемся тем, что любую комбинационную схему можно заменить на LUT, записав таблицу в ROM. Но как это сделать для такой большой таблицы? Воспользуемся другим трюком — сделаем наоборот: заменим EEPROM на нашу логическую схему и засунем её в программатор.

Неиспользуемые ноги соединены с землёй через резисторы. (Этого можно было и не делать, если покопаться в настройках программатора)
Теперь прочитаем нашу логическую схему как ROM и получим таблицу. Запишем её тем же программатором в реальный EEPROM, который поставим вместо схемы из отдельных элементов.

Хвост имеет длину (в наших ограничениях) от 2 до 8 клеток. Для хранения этой длины можно воспользоваться обычным счётчиком с входом разрешения счёта. По факту это будет такой же конечный автомат, у которого новое состояние S' будет равно S+1 или просто S (если счёт запрещён). Сам хвост (а точнее, направление, куда он растёт) мы будем хранить в двух регистрах по 8 бит. Теоретически, можно было бы взять готовые сдвиговые регистры (например, ИР8), но их под рукой не оказалось, поэтому в ход пошли те же самые ИР27. На каждом шаге в первый бит регистра записывается текущее направление движения головы, а во второй и последующий — значение предыдущего. Чтобы получить из него направление роста хвоста нам достаточно проинвертировать один бит. Можно сделать это сразу при записи, но я решил, что лучше оставить инверсию для оставшейся схемы.
Итого, наш автомат следующего хода принимает такой вид:
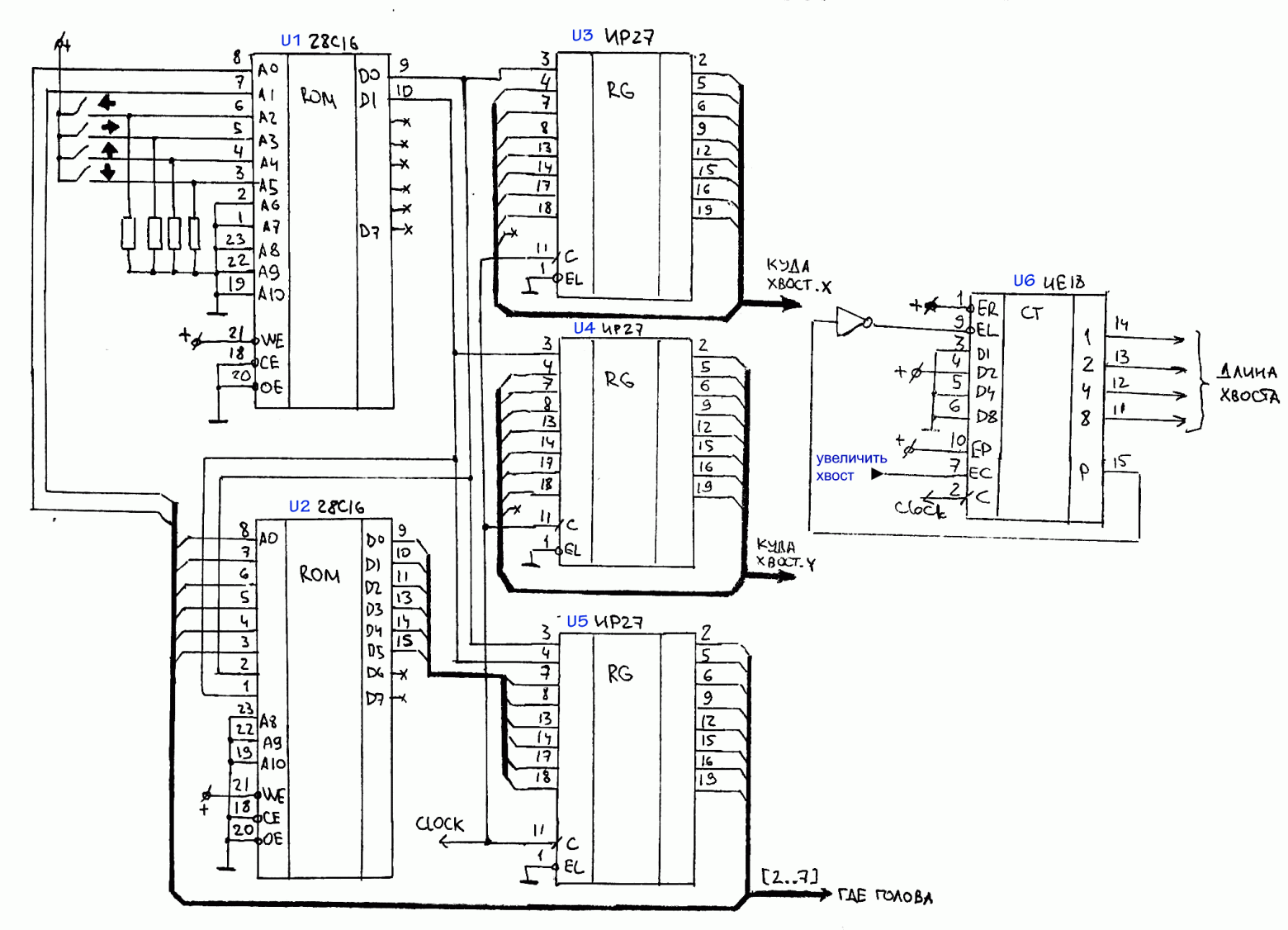
Эта картинка (как и все остальные) кликабельна.
Это довольно «чистая» (с теоретической точки зрения) часть схемы. Практически идеальный пример для output coded Moore machine. U1 отвечает за новое направление, U2 за положение головы, которые хранятся в U5. Для хвоста используются U3 и U4, а его длина хранится (и увеличивается) в U6.
Дальше нам надо будет сделать отображение всего что у нас есть на экране, и там тоже будет КА, только в более грязном виде. А также примитивный генератор случайных чисел, переход между схемами с разным тактирующим сигналом и прочие хаки.
Надеюсь, что данная статья вас заинтересовала и я постараюсь побыстрее закончить вторую часть.
А если вы уже рвётесь в бой, запаслись макетными платами, микросхемами и точечными экранами, то к этой статье прилагается файл со схемой и прошивками ROM. Мини-спойлер: для повторения конструкции вам понадобятся примерно 6 макеток, 4 EEPROM 28C16 и чуть больше двух десятков других микросхем.
Ну и как полагается: лайк, шер, ретвит, подписывайтесь, жмите колокольчик, итд… )) А на сегодня всё, спасибо за внимание! Продолжение следует…
Архив с прошивками ROM и общей схемой
UPD: вторая часть доступна по ссылке.

Игра Snake (она же змейка, питон, удав и т.д.) широко всем известна. Родом она из далёких 70-х, но я не буду повторять её историю, которую вы можете почитать в википедии или множестве статей на Хабре. Игра имеет достаточно простые правила и при этом затягивающий геймплей )) Благодаря этому её часто используют для туториалов или примеров кода. На языках программирования высокого уровня сделать такую игру достаточно легко. Но вот в более ограниченных условиях начинается самое интересное, например реализация на LabVIEW. Есть также множество вариантов на FPGA: ссылка 1, ссылка 2, ссылка 3, ссылка 4. Но ещё не было ни одного варианта на отдельных ТТЛ-микросхемах стандартных серий. Значит этим мы и займёмся.
Казалось бы, самыми близкими для нас являются решения на FPGA и оттуда можно много позаимствовать? Но во всех вариантах, которые я посмотрел, с лёгкостью разбрасываются регистрами налево и направо. Например, очень часто выделяют для каждой клетки поля отдельный бит или число. С рассыпухой мы так поступить не можем, ведь каждый новый регистр — это отдельная микросхема, которую надо где-то разместить, а потом ещё и соединить. Поэтому мы перечеркнём весь накопленный другими разработчиками опыт и будем делать всё с нуля. В качестве бонуса будем собирать всё на отечественных (а лучше — советских) микросхемах серии к555/кр1533, за исключением ПЗУ, которые придётся взять свежие.
Постановка задачи
У нас будут такие ограничения: поле размером 8×8 клеток (китайская светодиодная матрица), длина хвоста 8 клеток. Змейка может проходить через стены, а пересечение с хвостом мы поначалу обрабатывать не будем (дабы не усложнять конструкцию, добавить это можно потом). Чтобы описать всё состояние игры нам понадобится:
- Положение головы (X=0..7,Y=0..7, 6 бит)
- Направление движения (↑↓←→, 2 бита)
- Положение яблока (X,Y, 6 бит)
- Длина хвоста (0..7, 3 бита)
- Положение клеток хвоста (от 0 до 7 штук по 6 бит каждая)
Итого получается 65 бит, даже если брать регистры по 8 бит каждый, то только на хранение состояния понадобится 8 таких микросхем (и ещё один триггер), это довольно много.
Но хвост не может располагаться где ему вздумается, он «растёт» от головы. Поэтому мы можем хранить не полные координаты каждой секции хвоста, а только направление в какую сторону от предыдущей клетки (или головы) его надо нарисовать. Тогда вместо 6×8=48 бит нам понадобится 4×8=16 бит, а это уже экономия целых четырёх корпусов регистров!
Автоматы
Попробуем сделать всё на автоматах, похожих на автоматы Мура или Мили. Для реализации такого автомата достаточно иметь немного памяти состояний (регистр) и комбинационную логику для перехода между ними.

Картинка из википедии
Обычно конечный автомат описывают в виде графа состояний и переходов между ними. Иногда удобнее составить таблицу переходов в новое состояние, простейший пример (из википедии):

Больше информации и красивых картинок вы можете найти, например, в этой статье на Хабре
Небольшое отступление
В отечественной литературе, бывает, делят автоматы на имеющие жёсткую логику и программируемую. Я считаю такую дискриминацию несправедливой, ведь ROM по сути является такой же комбинационной схемой, и любую комбинационную схему можно заменить на ROM. (Как и наоборот, и этим мы воспользуемся чуть позже).
Такой пример с красивой картинкой можно найти, например, тут.
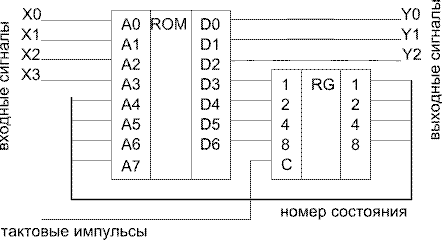
Все наши автоматы будут очень сильно напоминать эту схему, но я не буду заниматься «автоматным шовинизмом» и выделять одну реализацию КА среди других.
Такой пример с красивой картинкой можно найти, например, тут.

Все наши автоматы будут очень сильно напоминать эту схему, но я не буду заниматься «автоматным шовинизмом» и выделять одну реализацию КА среди других.
У змейки различных состояний (если не учитывать положения яблока) может быть 2^8+2^10+...+2^24 ≈ 32 миллиона. Расписать их в таблице, а уж тем более нарисовать граф переходов не представляется возможным. Но бóльшая часть переходов вполне однотипные (голова передвигается только на одну соседнюю клетку, а хвост продвигается по одной секции за ход). В таком случае мы можем описывать не каждое отдельное состояние, а сформулировать новое состояние в виде функции от предыдущего. Более того, всю игру мы можем разбить на несколько параллельных автоматов: 1) автомат направления, 2) автомат положения головы, 3) автомат для хвоста. И задать каждый из них так, как будет удобнее:
1) входы, направление │ новое направление
────────────────────┼───────────────────
← ←/↓/↑ │ ←
← → │ →
↑ ↑/←/→ │ ↑
↑ ↓ │ ↓
...итд... │
2) направление, голова │ новая голова
─────────────────────┼──────────────
← (x,y) │ (x-1, y)
→ (x,y) │ (x+1, y)
↑ (x,y) │ (x, y-1)
↓ (x,y) │ (x, y+1)
3) направление, хвост │ новый хвост
─────────────────────────────────────────┼──────────────────────────
← (t1,t2,t3,t4,t5,t6,t7,t8) │ (←,t1,t2,t3,t4,t5,t6,t7)
...итд... │
Направление
Начнём с автомата направления. Если хорошо подумать, то можно собрать его на отдельной логике. Но, поскольку задача в целом и так немаленькая, я решил, что проще будет сделать lookup table из EEPROM, а таблицу переходов записать вручную. Она будет иметь 6 входов, а значит только 64 значения, которые мы можем просто вбить в hex-редактор.

Голова
Для автомата положения головы написать такую таблицу будет намного сложнее. Но она содержит по сути только 2 операции: +1 и -1. Их можно реализовать на 4-х разрядном сумматоре К155ИМ6. Для +1 мы будем складывать нашу координату с b'0001, а для -1 с b'1111 (что собственно и есть -1 в дополненительном коде). Нам понадобятся два сумматора (для x и y), немного логики, а хранить состояние мы будем в 8-битном регистре ИР27 (их нам пригодится ещё много):

Соберём это на плате, а для проверки сразу подключим светодиодную матрицу с двумя дешифраторами. Дешифратор с инверсными выходами — ИД7, а для прямого можно было бы взять К561ИД1 (CD4028), но у меня под рукой его не было. Другой вариант — взять 8 транзисторов в качестве ключей, но делать этого не хотелось, поэтому пришлось бездарно потратить ещё один EEPROM (записав туда всего лишь 8 ячеек).

Логика нового положения головы на отдельной плате сверху
Ещё одно отступление
Сделаем небольшую передышку и сэкономим макетную плату (и несколько корпусов микросхем). Мы снова воспользуемся тем, что любую комбинационную схему можно заменить на LUT, записав таблицу в ROM. Но как это сделать для такой большой таблицы? Воспользуемся другим трюком — сделаем наоборот: заменим EEPROM на нашу логическую схему и засунем её в программатор.

Неиспользуемые ноги соединены с землёй через резисторы. (Этого можно было и не делать, если покопаться в настройках программатора)
Теперь прочитаем нашу логическую схему как ROM и получим таблицу. Запишем её тем же программатором в реальный EEPROM, который поставим вместо схемы из отдельных элементов.

Хвост
Хвост имеет длину (в наших ограничениях) от 2 до 8 клеток. Для хранения этой длины можно воспользоваться обычным счётчиком с входом разрешения счёта. По факту это будет такой же конечный автомат, у которого новое состояние S' будет равно S+1 или просто S (если счёт запрещён). Сам хвост (а точнее, направление, куда он растёт) мы будем хранить в двух регистрах по 8 бит. Теоретически, можно было бы взять готовые сдвиговые регистры (например, ИР8), но их под рукой не оказалось, поэтому в ход пошли те же самые ИР27. На каждом шаге в первый бит регистра записывается текущее направление движения головы, а во второй и последующий — значение предыдущего. Чтобы получить из него направление роста хвоста нам достаточно проинвертировать один бит. Можно сделать это сразу при записи, но я решил, что лучше оставить инверсию для оставшейся схемы.
Схема
Итого, наш автомат следующего хода принимает такой вид:

Эта картинка (как и все остальные) кликабельна.
Это довольно «чистая» (с теоретической точки зрения) часть схемы. Практически идеальный пример для output coded Moore machine. U1 отвечает за новое направление, U2 за положение головы, которые хранятся в U5. Для хвоста используются U3 и U4, а его длина хранится (и увеличивается) в U6.
Дальше нам надо будет сделать отображение всего что у нас есть на экране, и там тоже будет КА, только в более грязном виде. А также примитивный генератор случайных чисел, переход между схемами с разным тактирующим сигналом и прочие хаки.
Подытог
Надеюсь, что данная статья вас заинтересовала и я постараюсь побыстрее закончить вторую часть.
А если вы уже рвётесь в бой, запаслись макетными платами, микросхемами и точечными экранами, то к этой статье прилагается файл со схемой и прошивками ROM. Мини-спойлер: для повторения конструкции вам понадобятся примерно 6 макеток, 4 EEPROM 28C16 и чуть больше двух десятков других микросхем.
Ну и как полагается: лайк, шер, ретвит, подписывайтесь, жмите колокольчик, итд… )) А на сегодня всё, спасибо за внимание! Продолжение следует…
Архив с прошивками ROM и общей схемой
UPD: вторая часть доступна по ссылке.
