neonkainside 18 сен 2021 в 02:08

На заре вычислительной техники, часть 1

11 мин

5.3K

Предисловие

В моей предыдущей статье на тему истории вычислительной техники речь шла о цифровых устройствах. К ним мы еще вернемся, а сегодня разговор пойдет про принципиально иной способ ~~считать~~ вычислять, а именно про аналоговые вычислительные машины (АВМ), т.е. вычислительную технику, которая оперирует напрямую аналоговым представлением данных. Оговоримся сразу, что задача данной статьи — не каталогизация всяких латунных механизмов, а рассмотрение развития принципов построения аналоговой вычислительной техники, так что некоторые устройства могут быть намеренно забыты.

Как закалялась бронза

Первой известной нам АВМ является т.н. антикитерский механизм. Этот непонятный бронзовый девайс был найден в 1900 году близ греческого острова Антикитера.

antikitera_orig
Фото антикитерского механизма из Википедии

Длившийся в течение почти всего XX века реверс-инжиниринг продемонстрировал, что этот кусок бронзы мог показывать положение Луны, Солнца, предсказывать лунные и солнечные затмения, не хватало только WiFi и AMOLED-дисплея. Основным инструментом исследования антикитерского механизма стало рентгенографическое исследование:

antikitera_xray
Антикитерский механизм, радиографическое исследование. The Antikythera Mechanism Research Project

В этом ролике можно ознакомиться с механизмом работы этого бронзового вычислителя. Попробуем разобраться с общими принципами:

antikitera_front
Внешний вид передней панели механизма

Верхняя стрелка указывает положение Солнца на Эклиптике (относительно знаков Зодиака), стрелка с шариком на конце показывает текущую фазу Луны (шарик сам по себе еще может вращаться) и её положение. Справа на корпусе установлена ручка, которая и приводит весь механизм в движение. Никакого фиксированного источника времени, как в механических часах, в схеме нет.

antikitera_back_up
Внешний вид верхней части задней панели механизма

Эта часть отвечает за показ текущего положения в 19-летнем Метоновом цикле, разбитом на 235 лунных месяцев. Вдоль надписей выточена спиральная бороздка, по которой скользит подвижная игла, установленная на стрелке.

antitkitera_back_down
Внешний вид нижней части задней панели механизма

Эта часть позволяет предсказать лунные и солнечные затмения в течение драконического периода. Механически индикатор устроен аналогично верхнему.

antikitera_gearbox
Внутреннее устройство механизма

Не смотря на кажущуюся сложность, идея очень проста. От приводной ручки вращение передаётся на большую передаточную шестерню, с которой, через шестерни различных диаметров, раздаётся на стрелки. Таким образом все соотношения между угловыми скоростями валов линейные, т.е. вида

$\omega_{input} = K_{n} \omega_{n}$

где $\omega_{input}$ — угловая скорость приводной ручки, $\omega_{n}$ — угловая скорость $inline$ -й стрелки, $K_{n}$ — передаточное число. Как видно, такое устройство уже может умножать и делить вещественные числа, но только на фиксированные коэффициенты.

Я нашел в закромах у дедушки странную линейку

Следующий значимый шаг в развитии аналоговой вычислительной техники сделал английский математик Уильям Отред, который предложил прообраз логарифмической линейки. Принцип этого девайса прост и изящен, он использует следующий факт:

$display$

$log(x) - log(y) = log (\frac{x}{y})$

Таким образом, если мы научимся получать логарифмы чисел, то будем легко умножать и делить. На первый взгляд, мы только усложнили себе задачу, но рассмотрим следующую конструкцию:

log_line

Схема простейшей логарифмической линейки из Википедии

У нас есть 2 линейки, каждая из которых размечена в логарифмическом масштабе, теперь мы хотим умножить 2 на 3. Для этого сдвигаем верхнюю линейку до шкалы 2 на нижней. Длинна суммарного отрезка от шкалы 1 на нижней линейке до шкалы 3 на верхней линейке будет равна искомому произведению $inline$ . Реализация деления в таком устройстве тоже очевидна, Поделим, например, 8 на 4, т.е. совместим шкалу 8 нижней линейки со шкалой 4 верхней (получится та же ситуация, что и на рисунке), т.е $log (\frac{8}{4}) = log (8) - log (4) = log (2)$ . Логарифмические линейки позволили помимо этого получать значения тригонометрических функций и возводить в степень, а также банально складывать. Как это делается на их потомках из XX века можно почитать тут. Логарифмические линейки поселились на столах всех инженеров и научных работников и активно использовались вплоть до 80-х годов XX века, когда их, наконец, смогли выселить оттуда инженерные калькуляторы и персональные компьютеры.

Как реализовать логарифмическую шкалу? (данный кусок текста должен был быть под спойлером но почему-то формулы и ссылки под ним безбожно глючат)
Когда я дописал этот раздел, я несколько призадумался. Вот я такой умный, придумал логарифмическую линейку. А как, собственно, нанести логарифмическую шкалу, если у меня нет калькулятора? Честно говоря я не нашел упоминании о способе, которым пользовались создатели первых линеек, но мне на ум пришло 2 варианта:

Создать шкалу на базе $log_{2}(x)$ , т.е. эквидистантно расставить 1 2 4 8 ...
Воспользоваться тем фактом, что функция $inline$ обратна к функции $e^{x}$ и найти такой процесс, график какой-либо из величин в котором даёт такую кривую. Например затухающие колебания. Пишите ваши варианты в комментариях.

Как найти площадь Ленина?

Итак, настал XIX век, мы умеем вычислять значения функций, производить арифметические операции над натуральными числами. Настало время решить следующую насущную задачу — нахождение определённого интеграла функции $inline$ в промежутке $inline$ , где $inline$ . В русских словах — научиться находить площадь под кривой вида $inline$ . Рассмотрим задачу, что называется, на пальцах:

integral
Разбиение площади под интегрируемой функцией на прямоугольники равной ширины

Определённым интегралом данной функции будет сумма площадей таких прямоугольников при стремлении их ширины к нулю. Находить площадь прямоугольника просто, нужно умножать ширину на высоту, что умеет делать даже антикитерский механизм, но высота его в каждой точке графика разная, а значит нам нужен хитрый вариант антикитерского механизма, который умеет менять передаточное число произвольным образом. Такой девайс сконструировал в 1804 году Иоганн Герман.

planimetr_orig
Оригинальный чертёж планиметра Германа

По этому чертежу не так-то просто понять, что происходит, так что посмотрим на 3D модель, представленную в статье [1]:

planimetr_3D
3D-модель планиметра Германа

На схеме 1 — игла, которая идет вдоль интегрируемой кривой, 2 — подвижная штанга, при помощи тросика вращающая конус 4, установленный в раме 3, которая может свободно перемещаться вдоль станины 8. Конус вращает колесико 5, положение которого на конусе задаётся треугольной планкой 6. Колесико связано со счетчиком оборотов 7. Штанга двигается вдоль оси X, вращая конус. В зависимости от текущего значения Y система конус-колесико имеет разное передаточное число, так как чем меньше значение Y в данной точке кривой (задаётся перемещением рамы по станине), тем выше по треугольной планке поднимается колесико и тем меньше радиус конуса в этом месте, а значит тем меньше оборотов оно сделает за один оборот конуса. В этом ролике можно ознакомиться с действом в динамике, а также увидеть, что это устройство легко находит и площади замкнутых фигур.

planimetr_real
Отличная иллюстрация из этой статьи

Отметим, что планиметры дожили до наших дней и их даже можно купить в магазине. Их принцип действия несколько отличается от приведенных мной примеров, это так называемые полярные планиметры, но они являются прямыми потомками первых интеграторов.

Латунная Ванга

В XIX веке появился еще один интересный класс вычислительных устройств. Если не по сути, то по размерам он уже напоминал будущие шкафы первых компьютеров и был значительно сложнее, чем рассмотренный выше планиметр. Как и все рассмотренные нами ранее устройства, он был строго специализирован. Его предназначение — предсказание приливов. И тут многие удивятся. Тоже мне задача! Вон греки предсказывали движение планет и затмения, а тут какие-то приливы. А задача то оказалась не так проста. Не хочу углубляться в теорию приливов, буду смотреть на неё как гробовщик на людей (с) мой научник.

Перл моего научника

Как-то раз, на очередном аспирантском отчете, я перед толпой скучающих математиков несколько вольно что-то брякнул про численные методы. А диссертация моя не столько про сами численные методы, сколько про оптимальные архитектуры для них. На меня почуяв запах крови сразу набросились с расспросами про всякие сходимости и невязки. Когда меня уже почти зажали в угол моих математических познаний, встал мой научник и сказал следующее: "Вот смотрите, коллеги. Аркадий Петрович, например, хороший художник, Валерий Сергеевич неплохой спортсмен, а Иван Трофимович отлично поёт. А гробовщик смотрит на Аркадия Петровича — видит метр восемьдесят, смотрит на Валерия Сергеевича — видит метр шестьдесят пять. Вот и Александр смотрит на численные методы, как гробовщик на людей. Они ему интересны только с т.з. их свойств, как программы, исполняемой на железе."

Итак, для предсказания уровня прилива нам требуется вычислить значение выражения следующего вида:

$F(t) = A_{1} cos(\omega_{1}t + \phi_{1}) + A_{2} cos(\omega_{2}t + \phi_{2}) + A_{3} cos(\omega_{1}t + \phi_{3}) + ...$

Как видно, мы можем посчитать отдельные точки на логарифмической линейке, но наши текущие наработки не позволяют получить непрерывный график $inline$ . С этой задачей смогла справиться машина предсказания приливов, созданная в 1872 году небезызвестным Уильямом Томсоном. Его машина стала родоначальником целого семейства аналогичных агрегатов, проживших почти до середины XX века. Основным структурным элементом этой машины являлось остроумное устройство, т.н. шотландский механизм.

yoke

Наглядная гифка с Википедии

В этом механизме, при постоянной угловой скорости $\omega$ вала со штырем, амплитуда движения ползуна имеет следующий вид:

$F(t) = A cos(\omega t + \phi)$

Где $inline$ — расстояние от оси вала до штыря, $\phi$ — начальная фаза. Если не понятно, почему так:

cosinus

Чуть отредактированная иллюстрация, что такое косинус, из Википедии

Как видно, проекция радиус-вектора точки $inline$ на ось $inline$ равна $cos(\omega t)$ .

Итак, у нас есть источник гармонической составляющей для нашего вычислителя. Теперь нужно как-то их сложить. Решается эта задача просто — при помощи связи многих шотландских механизмов через систему блоков:

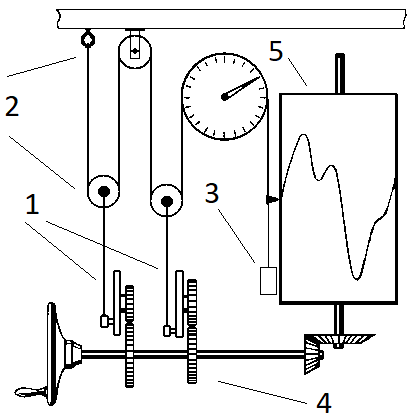
tide_predictor

Схема устройства машины. Оригинал тут

Здесь 1 — шотландские механизмы (вид сбоку), отвечающие за члены выражения 4. 2 — система блоков. 3 — отвес, 4 — приводной вал, 5 — барабан с бумагой для построения графика. Как видно, такая система обладает масштабируемостью для достижения большей точности. На сайте AMS есть очень наглядная модель на жабе.

tide_brazil
Машина предсказания приливов типичной конструкции. Фото отсюда

Вычислители из LEGO

Итак, мы научились интегрировать, вычислять синус и даже складывать. Но любой физик вопросительно посмотрит на нас и скажет, что это, конечно, замечательно, но ему бы решать дифференциальные уравнения, а лучше системы дифференциальных уравнений. Примерно это они и сказали. Настал XX век, потребовалось множество прикладных расчетов. Цифровые вычислители только-только пытались начать работать. На помощь пришли дифференциальные анализаторы. К сожалению эта глава получилась непропорционально большой, но тут уж ничего не поделать, устройства эти были значительно сложнее, чем все, построенное ранее. Будем разбираться в его блоках, постепенно усложняя целевое дифференциальное уравнение. Важной особенностью этих устройств стала блочная структура, которая сделала их практически универсальными решателями дифференциальных уравнений. Будем вводить их и рассматривать на ходу по мере усложнения решаемого уравнения. Первой нашей задачей станет:

$y^{,} = y$

Если вам не знакомо обозначение $y^{,}$ , то это упрощенная запись $\frac{dy(x)}{dx}$ . В такой постановке совершенно непонятно, с чего начать. Но можно переписать его в следующем виде:

$y = \int ydx$

И что теперь? А теперь мы вспомним, что интегрировать то мы уже умеем! Одним из основных блоков дифференциальных анализаторов стали интеграторы.

integrator

Схема работы интегратора [2]

Здесь каретка B может двигаться влево или вправо по параллельным направляющим в зависимости от направления вращения винта, задающего значение $inline$ интегрируемой функции. Диск D вращается с постоянной скоростью, задавая скорость изменения аргумента функции $inline$ . С диском соприкасается ролик радиуса R, угловая скорость вращения которого очевидно меняется, при изменении y. Чувствуете эффект дежа вю? Да, это выглядит, как будто мы расплющили планиметр. Так и есть. А теперь мы провернем следующую хитрость:

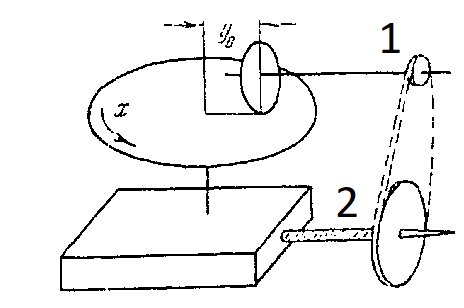
solver1

Схема решения уравнения (6)

В этой конструкции с вала 2 мы будем получать текущее значение функции $inline$ . Давайте убедимся, что это так. Пусть угловая скорость диска $\omega$ . Длина дуги, которую проходит ролик за $inline$ времени:

$dL = \omega y(t) dt$

Тогда приращение числа оборотов ролика $inline$ :

$dn = \frac{\omega}{C} y(t) dt$

Где $inline$ — длина окружности ролика. Теперь, вспоминая, что мы соединили входной и выходной вал интегратора, т.е. $dn = \frac {dy}{dt}$ :

$\frac {dy(t)}{dt} = K y(t) dt$

Здесь в $inline$ мы спрятали все коэффициенты. Если потребуется, мы можем свести их к 1 меняя передаточное число обратной связи. Итак мы показали, что наша схема эквивалента уравнению (6) и получили машину для его решения.

1st_sch

Схема решения уравнения 6

На $inline$ подается постоянная угловая скорость, с вала $inline$ получаем решение. На пересечениях валов кружками отмечены передачи с вала на вал. Значок снизу — интегратор.

Для закрепления понимания попробуйте разобраться, как работает схема решения для следующего уравнения:

$y^{,} + \int ydx = c$

И схема для него:

2nd_sch

Схема решения уравнения 11

Теперь перейдем к более сложному и полезному на практике случаю:

$y^{,,} + F(y) = 0$

Или в более удобоваримом для имеющейся у нас аппаратуры виде:

$y^{,} = -\int F(y)dx + c$

Как подать в нашу систему $inline$ ? Для этого нам понадобится еще одно устройство, операторная доска.

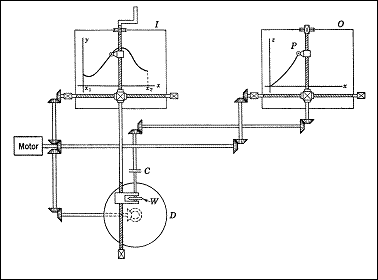
operator_board

Схема работы операторной доски отсюда

Motor подает на вал вращение с постоянной угловой скоростью. Круг снизу — диск уже знакомого нам интегратора, только у него двигается на диск D, а рамка с роликом W. I — операторная доска. Вертикальный червяк перемещается с постоянной скоростью, т.к. его двигает горизонтальный червяк с приводом от Motor. Оператор при помощи ручки вращает вертикальный червяк таким образом, чтобы указатель на нем удерживался графике. Таким образом червяк точно передаёт значение оси $inline$ на интегратор. Теперь давайте вставим этот девайс в нашу схему для решения дифференциального уравнения.

Схема для решения уравнения 12

Здесь появился еще один элемент, обозначенный на пересечении валов, как 2 концентрических круга. Это такая же передача с вала на вал, только меняющая направление вращения вала на противоположное. Заметим также, что на схеме работы операторной доски появился еще один полезный элемент, приёмная доска O, на которой строится график решения задачи. Принцип как и у операторной доски, только вместо собственно оператора у неё схема для решения задачи.

Двигаемся дальше. Теперь мы познакомимся с еще одной важной арифметической операцией. Сложением. Для начала рассмотрим задачу, для которой оно нам понадобится [3]:

$y^{,,,} = (2yy^{,,} - sin(y^{,}))^2$

adder

Схема для решения уравнения 14

Здесь прямоугольником со значком $\Sigma$ обозначен сумматор. Хочется обратно в раздел про логарифмическую линейку, правда? Базируется принцип действия сумматора на дифференциальной передаче. Более известен он в среде автомобилистов (очень рекомендую всем, кто не знает, что это такое, посмотреть этот ролик ), нежели среди разработчиков вычислительной техники.

adder

Схема сумматора, взятая из [4]

На схеме коническая шестерня a жёстко закреплена на валу A, на валу B коническая шестерня b. Конические шестерни c и d закреплены на валу D, но могут свободно вращаться вокруг него. Вал D закреплен в корпусе дифференциальной передачи. На этом же корпусе закреплена цилиндрическая шестерня S $_{1}$ (вал B просто проходит сквозь неё без зацепления). Шестерня S $_{1}$ сцеплена с шестерней S $_{2}$ , которая приводит в движение вал C (для простоты будем считать их передаточное число равным 1). Давайте разберемся, как это работает.

Для начала будем считать вал B неподвижным, а вал A вращающимся с угловой скоростью $\alpha$ , а радиусы всех конических шестерней положим равными $inline$ . Тогда в точках соприкосновения шестерней a и c и a и b линейная скорость вращения очевидно будет $r\alpha$ , а в центах шестерней c и d (помним, что b неподвижна) очевидно $r\alpha /2$ . Таким образом корпус дифференциальной передачи, а значит и шестерня S $_{1}$ , и вал C, сцепленный с ней через S $_{2}$ , будут вращаться с угловой скоростью $\alpha /2$ . Если мы теперь запустим вал B с угловой скоростью $\beta$ , то, проделав аналогичные выкладки, получим на валу C угловую скорость $(\alpha + \beta)/2$ . Мы научились складывать! Вычитать, кстати, тоже, можете этот факт легко проверить, изменив знак одной из скоростей.

real_adder

Сумматор "в железе" из IPSJ Computer Museum

Здесь разобранная нами конструкция вывернута наизнанку. Роль валов A и B играют большие шестерни слева и справа, а вал C пропущен внутри левой шестерни и жёстко закреплен в валу D. Вот в этом видео можно самостоятельно найти все описанные мной детали конструкции дифференциального анализатора. На большие шестерни на выходах из интеграторов пока не обращайте внимания, это усилители, о которых я сделаю отдельную небольшую заметку, т.к. это технологический нюанс, не имеющий отношения непосредственно к математике.

real_device

Реальный музейный анализатор отсюда

Здесь можно видеть сразу 3 интегратора, на дальнем плане операторная доска, на переднем — приемная доска. И все-таки, не смотря на наши возросшие возможности, чего-то не хватает… Умножения! Рассмотрим пример из [5]:

$v(x) = \frac{1}{x} \int \Psi(x)^{2}dx + \int \frac{\Psi(x)^{2}dx}{x}$

mult

Схема решения уравнения 15

Как видно, нам здесь потребовалось умножать $\int \Psi(x)^2dx$ на $\frac{1}{x}$ . Имеющимися у нас средствами сделать это не получается, так что на помощь нам приходит т.н множительная доска, (или MULTYPLIER UNIT на схеме). Две входящие в неё стрелки — валы, передающие значения сомножителей. На выход соответственно подаётся результат умножения в виде произведения угловых скоростей входящих валов. Как же это работает и зачем там сбоку приделана ручка?

mult_sch

Структурная схема множительной доски

Что за ужас тут творится, спросите вы? Все просто. На валы $inline$ и $inline$ подаются сомножители. Таким образом вращение вала $inline$ при помощи ползушки $inline$ и штыря S поворачивает вокруг оси O линейку D. Вал В, двигая ползушку $inline$ , двигает влево или вправо станину с закрепленной на ней ползушкой $inline$ , которая в свою очередь приводится в движение вращением вручную ручки H. Пусть угол поворота винта $inline$ будет $inline$ , а угол поворота вала В будет $inline$ . Так как $\Delta OCП_3$ и $\Delta OPU$ подобны, то:

$\frac{f_1}{h} = -\frac{y}{f_2}$

Таким образом, если оператор при помощи винта H будет удерживать марку U на прямой OD, то угол вращения вала, связанного с винтом H будет пропорционален y. Таким образом мы можем получить на этом валу искомую угловую скорость.

Механические дифференциальные анализаторы пережили Вторую мировую войну. Их более простые собратья отважно сражались на ней, наводя зенитные пушки и прокладывая курс самолетам. Компьютеры тех лет были еще слишком слабы, чтобы тягаться с анализаторами в их задачах, так что эволюция продолжилась. Про электронные и гидравлические АВМ продолжу в следующей статье. А пока, спасибо за внимание.

PS: У меня упорно не работают спойлеры маркдауна. Что я делаю не так?

[1] Cones, Disks, Wheels and Spheres for Area and Integration from Bavaria to Boston and beyond Stefan Drechsler, Barbara Haeberlin Cambridge, MA, September 2011

[2] И.С. Брук, Машина для интегрирования дифференциальных уравнений, Москва, 1941

[3] Clayton Brooks, Saeed Keshavarzian, Bonita A. Lawrence, Richard Merritt, The Marshall Differential Analyzer Project: A Visual Interpretation of Dynamic Equations, Huntington, West Virginia, 2007

[4] Joseph Emil Kasper, Construction and application of a mechanical differential analyzer, State University of Iowa, 1955

[5] Samuel Hawks Caldwell, THE EXTENSION AND APPLICATION OF DIFFERENTIAL ANALYZER TECENIQUE IN THE SOLUTION OF ORDINARY DIFFERENTIAL EQUATIONS, Massachusetts Institute of Technology, 1926

Теги:

Хабы: