Скорость звука: каков ее предел?

Одна из основных задач какой-либо точной науки заключается в измерении и объяснении тех или иных процессов, а также их участников. За многие годы исследований, расчетов и споров научное сообщество пришло к пониманию того, что существуют определенные ограничения в некоторых явлениях. К примеру, скорость света в вакууме равна 299 792 458 м/с. Согласно специальной теории относительности, ничто не может двигаться быстрее. Другими словами, мы имеем верхний скоростной лимит для света. Однако такой лимит для скорости звука пока не был установлен. Ученые из Лондонского университета королевы Марии (Англия, Великобритания) провели расчеты, результатом которых стало открытие верхнего предела скорости звука. Что стало основой расчетов, каковы их результаты, и в каких областях можно применить новообретенные знания? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.

Основа исследования

Звук это волны механических колебаний в какой-либо среде. Скорость распространения этих волн напрямую зависит от самой среды. К примеру, в твердых объектах звук распространяется быстрее, чем в воздухе. Однако и тут могут быть флуктуации в измерениях, поскольку важна не только среда как таковая, но и ее состояние (температура, давление и т.д.).

Логично, что скорость звука сложно назвать константой, так как в разных условиях она будет своя: в воздухе это 331 м/с, в воде 1500 м/с (тут будут вариации в зависимости от температуры, давления и солености воды), а в стекле 4800 м/с.

Но как же рассчитать верхний лимит скорости звука?

Как напоминают нам ученые, некоторые важные свойства конденсированных фаз* определяются фундаментальными физическими константами.

Конденсированные фазы* — состояние вещества, когда число его компонентов (атомов, молекул и т.д.) крайне велико, а взаимодействия между компонентами очень сильны. К числу таких фаз можно отнести и твердые вещества, и жидкости.

Радиус Бора позволяет охарактеризовать межатомное расстояние в ангстрем (1 Å = 0.1 нм) масштабах с точки зрения массы электрона (me), заряда (e) и постоянной Планка (h). Эти же фундаментальные константы входят в энергию Ридберга*, задавая масштаб характерной энергии связи в конденсированных фазах и химических соединениях.

Постоянная Ридберга* — предельное значение наивысшего волнового числа любого фотона, который может быть испущен атомом водорода. Также эта постоянная определяет волновое число фотона с наименьшей энергией, способного ионизировать атом водорода в его основном состоянии.

Тем не менее крайне важную роль в физике играют безразмерные и не зависящие от единиц измерения константы. К ним относятся постоянная тонкой структуры* и отношение массы протона к массе электрона*.

Постоянная тонкой структуры* (⍺) — фундаментальная физическая постоянная, которая характеризует силу электромагнитного взаимодействия. Эта постоянная определяет размер крайне малого изменения величины энергетических уровней атома и образования тонкой структуры, которые являются набором узких и близких частот в его спектральных линиях.

Отношение массы протона к массе электрона* (m_p/m_e — константа, равная 1836,15267261.

Объединение этих констант позволяет определить новую безразмерную константу, описывающую верхнюю границу скорости звука (v_u) в конденсированных фазах (формула №1):

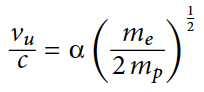
где c — скорость света в вакууме, ⍺ — постоянная тонкой структуры, m_p/m_e — отношение масс протона и электрона, v_u — верхний предел скорости звука.

Подтверждение верности данной формулы было получено благодаря многочисленным экспериментам и моделированию атомарного водорода.

Результаты исследования

Авторы сего труда отмечают, что существует два подхода к определению v (скорости звука). Один поход начинается с оценки упругости системы, а второй — с оценки ее вибрационных свойств. Оба подхода дают сопоставимые результаты (приготовьтесь, формул будет немало).

Что касается упругости системы, то продольная скорости звука равна: v = (M/p)^1/2, тогда как M = K + 4/3G, где K — объемный модуль упругости; G — модуль сдвига; p — плотность.

Было установлено, что упругие постоянные определяются плотностью электромагнитной энергии в конденсированных фазах. В частности, была установлена четкая связь между модулем объемной упругости (K) и энергией связи (E): K = f E/a³, где а — межатомное расстояние, f — коэффициент пропорциональности.

Это соотношение может быть выведено с точностью до константы, задаваемой второй производной функции, представляющей зависимость энергии от объема. Для наиболее прочно атомарно связанных твердых тел f варьируется в диапазоне от 1 до 4. Также стоит учесть и коэффициент пропорциональности между M и E/a³, который варьируется от 1 до 6.

Объединение v = (M/p)^1/2 и М = f E/a³ в результате дает v = f^1/2(E/m)^1/2, где m — масса атома или молекулы (в данном случае использовалась m = pa3). Коэффициент f^1/2 составляет примерно от 1 до 2 и может быть исключен в случае приблизительной оценки v. В таком случае мы получим (формула №2):

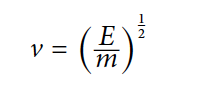
Энергия связи в конденсированных фазах определяется ридберговской энергией порядка нескольких электрон-вольт (формула №3):

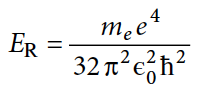
где е — заряд электрона, m — масса электрона. E_R используется для оценки величины энергии связи (E).

Используя E = E_R из формулы №3 в формуле №2 мы получим (формула №4):

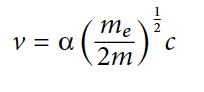
где ⍺ = (1/4πϵ₀)(e²/hc) — постоянная тонкой структуры.

Такой же результат, как и в формуле №4, можно получить и посредством второго подхода, где основной акцент поставлен на рассмотрении вибрационных свойств системы.

Продольную скорость звука (v) можно оценить как фазовую скорость по кривой продольной дисперсии [ω = ω(k)] в приближении Дебая: v = ω_D/k_D, где ω_D это частота Дебая; k_D — волновой вектор. Применение k_D = π/a (a — межатомное/межмолекулярное расстояние) приводит к (формула №5):

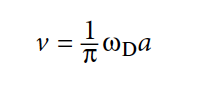
Как мы уже рассматривали ранее, характеристики межатомного разделения описываются радиусом Бора (a_B) в ангстрем масштабах (формула №6):

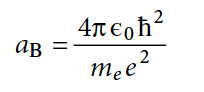
Далее было использовано отношение между фононной энергией (hω_D) и E. Фононная энергия может быть выражена как h(E/ma²)^1/2. Если взять отношение hω_D/E, использовать а = a_B из формулы №6 и E = E_R из формулы №3, то в результате получится (формула №7):

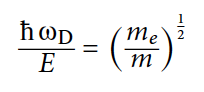
Применение формулы №7 в формуле №5 дает следующее (формула №8):

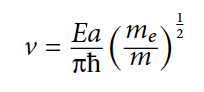
Сравнение данных расчетов с первым подходом указывает на то, что второй подход использует больше приближений, потому ученые решили на дальнейших этапах исследования использовать первый подход (формула №4), который является более точным.

Далее выбранный подход был проверен на более практическом уровне.

m_e характеризует электроны, которые отвечают за взаимодействия между атомами. Электронный вклад далее отражается в коэффициенте ⍺c (⍺c ∝ e²/h), который представляет собой скорость электронов в модели Бора. Ученые отмечают, что ⍺с и v не зависят от c. Использование формулировки v в виде ⍺с в формуле №4 обусловлено двумя факторами.

Во-первых, так намного удобнее и информативнее представлять границу в отношении v_u/c, что обычно применяется в отношении скорости Ферми и скорости света (v_F/c).

Во-вторых, именно ⍺ (наряду с m_p/m_e) имеет фундаментальное для стабильности протонов и обеспечения синтеза тяжелых элементов и, следовательно, существования твердых тел и жидкостей, в которых звук может распространяться.

m формула №4 характеризует атомы, участвующие в распространении звука. Его масштаб задается массой протона m_p: m = Am_p, где A — атомная масса. Учитывая, что А = 1, а m = m_p, применение формулы №4 позволяет определить значение верхней границы скорости звука (формула №9):

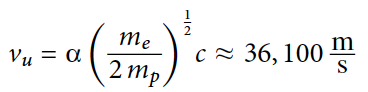
Таким образом было показано, что v_u зависит только от фундаментальных физических констант, включая безразмерную постоянную тонкой структуры и отношение масс протона и электрона.

Вышеуказанная формула является расширенным вариантом формулы №4 для атомарного водорода. Объединение формул №4 и №9, при учете m = Am_p, позволяет получить (формула №10):

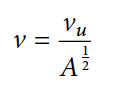
Что ж, теперь можно немного отдохнуть от формул и приступить к обсуждению расчетов и экспериментов.

Ученые отмечают, что хоть скорость звука определяется модулями упругости и плотностью, они существенно отличаются в зависимости от типа связи: сильные ковалентная, ионная или металлическая связи, обычно дающей большую энергию связи, промежуточные водородные связи, а также слабые дипольные и ван-дер-ваальсовые взаимодействиям. Модули упругости и плотность также меняются в зависимости от конкретной конструкции, которую принимает система. Кроме того, тип связи и структура сами по себе взаимозависимы: ковалентная связь приводят к образованию открытых структур, а ионная — плотноупакованных. Следовательно, скорость звука для конкретной системы не может быть предсказана аналитически и без явного знания структуры и взаимодействий внутри нее, подобно другим системно-зависимым свойствам, таким как вязкость или теплопроводность.

Тем не менее зависимость v от m или A может быть изучена в семействе элементарных твердых тел. Элементарные твердые вещества не имеют смешанных особенностей, существующих в соединениях из-за смешанной связи между разными атомными разновидностями (включая смешанную ковалентно-ионную связь между одними и теми же парами атомов, а также разные типы связи между разными парами).


Изображение №1

Теория была проверена на практике с применением 36 различных элементарных твердых тел, в том числе полупроводников и металлов с большими энергиями связи. Результаты теоретических расчетов были объединены с результатами опытов на графике выше. Прямая линия на графике (формулу №10) оканчивается ее верхней теоретической границей (формула №9) для A = 1. Линейный коэффициент корреляции Пирсона*, рассчитанный для экспериментального набора (log A, log v), составил -0.71. Его абсолютное значение немного выше границы, условно разделяющей умеренную и сильную корреляции.

Коэффициент корреляции Пирсона* используется для изучения связи двух переменных, измеренных в метрических шкалах на одной и той же выборке.

Расчетные и экспериментальные значения v_u, показанные на графике прямой и пунктирной линиями, указывают на пересечение в точке 37.350 м/с, что подтверждает верность расчетных походов и, особенно, верность аппроксимации коэффициент в формуле №4, что дает хорошее согласование с экспериментальными данными.


Изображение №2

Далее было решено проверить согласование расчетных данных с экспериментальными с применением более широкого спектра образцов (133 образца). Экспериментальные значения v были меньше, чем верхняя теоретическая граница v_u в формуле №9. v_u примерно вдвое больше v в алмазе, это является самой высокой скоростью звука, измеренной в условиях окружающей среды.

Формула №10 может использоваться для приблизительного прогнозирования средней или характеристической скорости звука (v). A1/2, которая, согласно формуле №10, относится к скорости звука, варьируется по периодической таблице в диапазоне от 1 до 15 со средним значением 8. Согласно расчетам соответствующее значение v равно 4513 м/с. Это на 16% согласуется с 5392 м/с — средним значением по всем элементарным твердым телам, и на 14% с 5267 м/с — средним значением по всем твердым телам на графике выше.

В эксперименты также были включены данные по скорости звука в жидкости при комнатной температуре, которые варьируются от 1000 до 2000 м/с. Однако в высокотемпературных жидких металлах, таких как Al, Fe, Mg и Ni, v достигает более высоких значений в диапазоне от 4000 до 5000 м/с. Из этого следует, что скорость звука в жидкостях полностью удовлетворяет расчетную верхнюю границу скорости.

Ученые отмечают, что хоть приближения, использованные в некоторых формулах, и могут повлиять на вычисление v и его оценку, v_u все же формируется исходя из фундаментальных констант. Другими словами, в конечном итоге приближения не имеют столь значимого влияния.

Также было установлено, что рассчитанное значение верхней границы скорости звука применимо к твердым телам не только с сильной межатомной связью, но и со слабой. Формула №3, 6 и 7 предполагают, что валентные электроны непосредственно участвуют в связывании. Следовательно, они играют важную роль в системах с металлической, ковалентной и ионной связью. Несмотря на то, что связывание в твердых телах со слабой связью также имеет электромагнитное происхождение, слабые дипольные и ван-дер-ваальсовые взаимодействия приводят к меньшему E и, как результат, меньшему v. Потому из этого следует, что верхняя граница v_u применима и к слабосвязанным системам.

Ученые отмечают, что верхняя граница v_u соответствует твердому водороду с прочной металлической связью. Данная фаза вещества существует только при мегабарном давлении и динамически нестабильна при атмосферном давлении, где происходит образование молекул. Посему было решено провести расчеты v в атомарном водороде, чтобы подтвердить верность расчетов как таковых.

Расчеты скорость звука в атомарном водороде проводились с применением структуры I4₁/amd, которая является наилучшей структурой-образцом для твердого атомарного металлического водорода. Известно, что эта структура становится термодинамически стабильной в диапазоне давлений от 400 до 500 ГПа, ниже которого твердый водород является молекулярным твердым телом. Однако было обнаружено, что I4₁/amd динамически устойчива при давлениях выше примерно 250 ГПа, поэтому расчеты проводились в диапазоне давления от 250 до 1000 ГПа.


Изображение №3

На графике выше представлена скорость звука как функция давления и плотности. Рассчитанное значение скорости звука было ниже значения v_u в широком диапазоне давлений. Увеличение v выше расчетной верхней границы возникает лишь при давлении 600 ГПа и выше. Следовательно, при нормальных условиях скорость звука не будет превышать расчетную верхнюю границу.

Для более подробного ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых.

Эпилог

В данном труде ученые определили, что важнейшую роль в оценке максимально возможной скорости звука играют две фундаментальные константы — постоянная тонкой структуры и отношение массы протона к массе электрона.

Проведенные расчеты были проверены на практике с применением разнообразных материалов. Эксперименты позволили установить, что скорость звука должна уменьшаться с атомарной массой. Из этого следует, что максимальная скорость звука достигается в твердом атомарном водороде, который может существовать в таком виде лишь при очень высоком давлении. Тем не менее было установлено, что верхняя граница скорости звука в рамках данного исследования составляет 36100 м/с. С практической точки зрения, подобные исследования крайне важны для понимания тех или иных материалов, а также их свойств.

Естественно, ученые не намерены останавливаться на достигнутом. Их расчеты и соответствующие экспериментальные данные требуют перепроверки, уточнения и дополнительного подтверждения. В будущем данное исследование будет продолжено, а верхняя граница скорости звука может неожиданно сместиться в большую или меньшую сторону ввиду новых данных. Как бы то ни было, фундаментальный подход остается прежним, а сам факт лучшего понимания процессов, протекающих вокруг нас, позволяет с уверенностью смотреть на развитие данного исследования.

Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. :)

Немного рекламы

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?