9851754 26 авг 2021 в 13:02

Преобразования целевой переменной в задачах линейной регрессии

5 мин

Если у тебя есть целевая переменная и ты в отчаянии не знаешь, что с ней делать, и потерял всякий покой, потому что метрика не растет, загляни сюда, тебе может понравится...

Постановка задачи

Дан набор наблюдений вида $\{(x_1, y_1), (x_2,y_2), \dots,(x_n,y_n)\}$ , где $x,y \in \mathbb{R}$ т.е. x,y в нашем случае просто числа, рассматриваем одномерную регрессию с одним параметром. По этому набору мы хотим построить функцию a(x) , которая по заданному вычисляет значение . Предпологается, что- целевая переменная связанна с переменной таким способом:

$y =b+w*x+\epsilon,$

где $\epsilon$ - случайная величина, имеющая нормальное распределение с параметрам $N(\mu, \sigma)$ , - неизвестный коэффициент, который надо оценить из данных. Для упрощения будем считать, чт $b=0, \mu=0$ , поэтому $y =w*x+\epsilon$ . Так же считаем, что все наблюдения в выборке независимы.

Решение задачи

Известно, что если b - это число, а $\epsilon$ - случайная величина с нормальным распределением $N(\mu, \sigma)$ , то сумма $b+\epsilon$ есть так же случайная величина с распределением $N(\mu+b, \sigma)$ , т.е. прибавляя константу к случайной величине мы сдвигаем это распределение. Т.к. $y =w*x+\epsilon$ , то- случайная величина с нормальным распределением $N(w*x, \sigma)$ , а плотность распределения будет иметь вид:

$f(y) = \frac{1}{\sigma\sqrt{2\pi}}exp\left(-\frac{(y-w*x)^2}{2\sigma^2}\right)$

Поскольку в нашей выборке есть ${y_1, y_2, \dots,y_n}$ , то мы хотели бы так подобрать параметр w, чтобы вероятность увидеть именно такую выборку как у нас была бы максимальной (MLE). Поскольку y - непрерывная случайная величина, то максимизировать будем не вероятность, а плотность. Совместная плотность нашей выборки есть произведение плотностей каждой y_i :

$f(y_1)*f(y_2)*\dots*f(y_n) = \frac{1}{\sigma\sqrt{2\pi}}exp(-\frac{(y_1-w*x_1)^2}{2\sigma^2}) * \frac{1}{\sigma\sqrt{2\pi}}exp(-\frac{(y_2-w*x_2)^2}{2\sigma^2}) * \dots$

Обозначим это выражение как L(w) , которое мы будем рассматривать относительно параметра w. L(w) - называется функцией правдоподобия и ее мы будем максимизировать по параметру w. Теперь мы перемножаем все n слагаемых и упрощаем наше выражение, получив следующее:

$L(w) = \left(\frac{1}{\sigma\sqrt{2\pi}}\right)^n exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-w*x_i)^2\right)$

Мы можем убрать константу $\left(\frac{1}{\sigma\sqrt{2\pi}}\right)^n$ , поскольку это никак не повлияет на максимизацию, а так же взять логарифм натуральный от L(w) , поскольку логарифм это монотонная функция и она так же не повлияет на результаты, но выражение станет чуть приятнее:

$\log{L(w)} = -\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-w*x_i)^2$

Множитель перед суммой так же можем выбросить - не влияет на поиск оптимальных параметров и получим такую задачу - найти такое значение параметра w, которое максимизирует нашу функцию, или кратко:

$w = arg\max_{w \in \mathbb{R}} \left( -\sum_{i=1}^{n}(y_i-w*x_i)^2\right)$

В контексте нашей темы мы можем сделать следующие полезные выводы:

В нашей модели каждое значение целевой переменной получено из нормального распределения. Но ни откуда не следует, что построив гистограмму для ${y_1, y_2, \dots,y_n}$ она обязательно окажется нормальной мы увидим это дальше в примерах.
В модели не подразумевается, что все будут различны, а на практике часто так и происходит, что одному , соответствует сразу несколько ${y_{j1}, y_{j2}, \dots}$ , но гистограмма, построенная на ${y_{j1}, y_{j2}, \dots}$ обязанна с точки зрения нашей модели иметь нормальное распределение.

Далее можем пытаться решить задачу аналитически и найти производную и приравнять к нулю, использовать градиентный спуск или записать функцию правдоподобия в виде функции на python и передать оптимизатору из scipy. Я выбрал последнее и получил:

Настоящий коэффициент: 28.301, r2_score: 0.989
Коэффициент полученный MLE: 28.273, r2_score: 0.989
Коэффициент полученный регрессией из sklearn: 28.274, r2_score: 0.989

Данные генерились с помощью sklearn-функции make_regression. Видим, что коэффициент, полученный методом максимального правдоподобия совпадает либо незначительно отклоняется, если запускать с другим seed, или без него, с коэффициентом из sklearn LinearRegression, и равен реальному коэф.

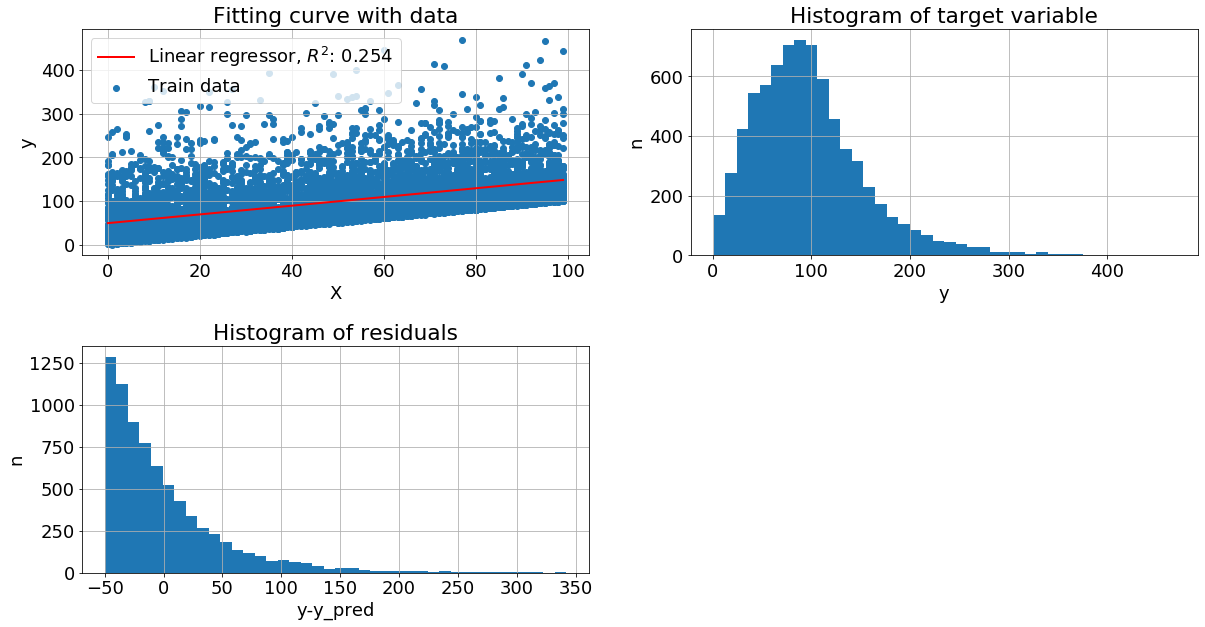
Рассмотрим графики:

Левый верхний - изображена диаграмма рассеяния обучающей выборки и построена линия линейной регрессии
Правый верхний - построена гистограмма распределения целевой переменной, просто plt.hist(y)
Левый нижний - вычислили разность между целевой переменной и прогнозом регресии, далее построили гистограмму остатков plt.hist(y-y_pred)

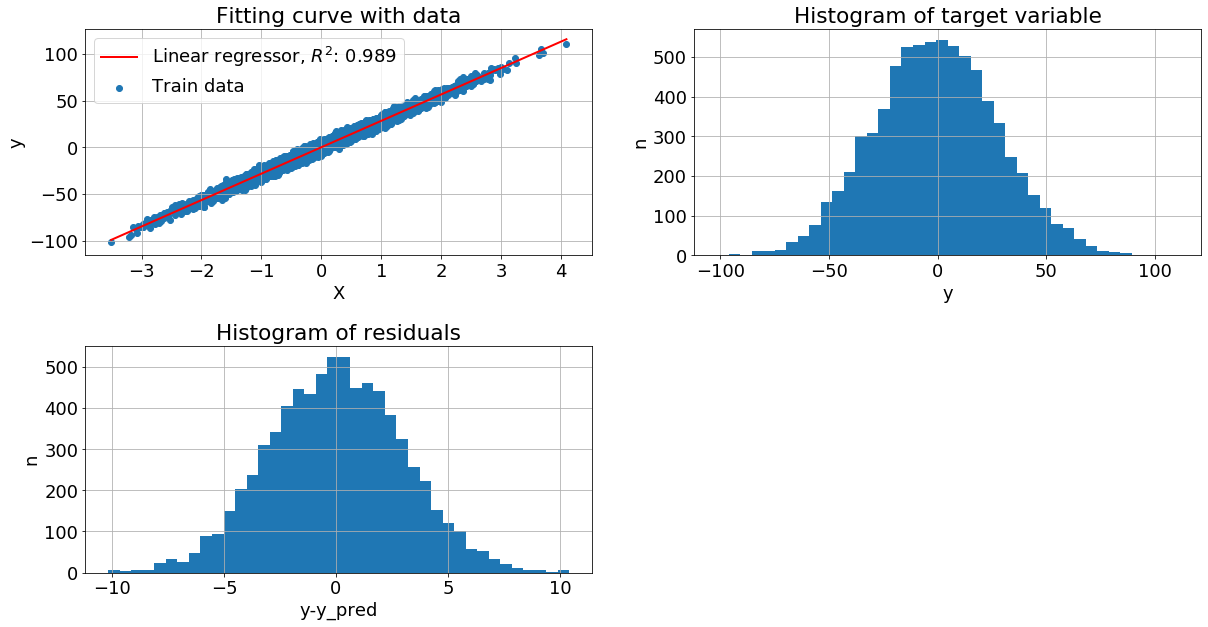
Оценивая "на глаз" распределение как целевой переменной, так и остатков видим, что они близко к нормальному. Теперь рассмотрим другие механизмы порождения данных, не только с нормальным шумом и с более сложной зависимостью y от x.

Различные модели порождения данных

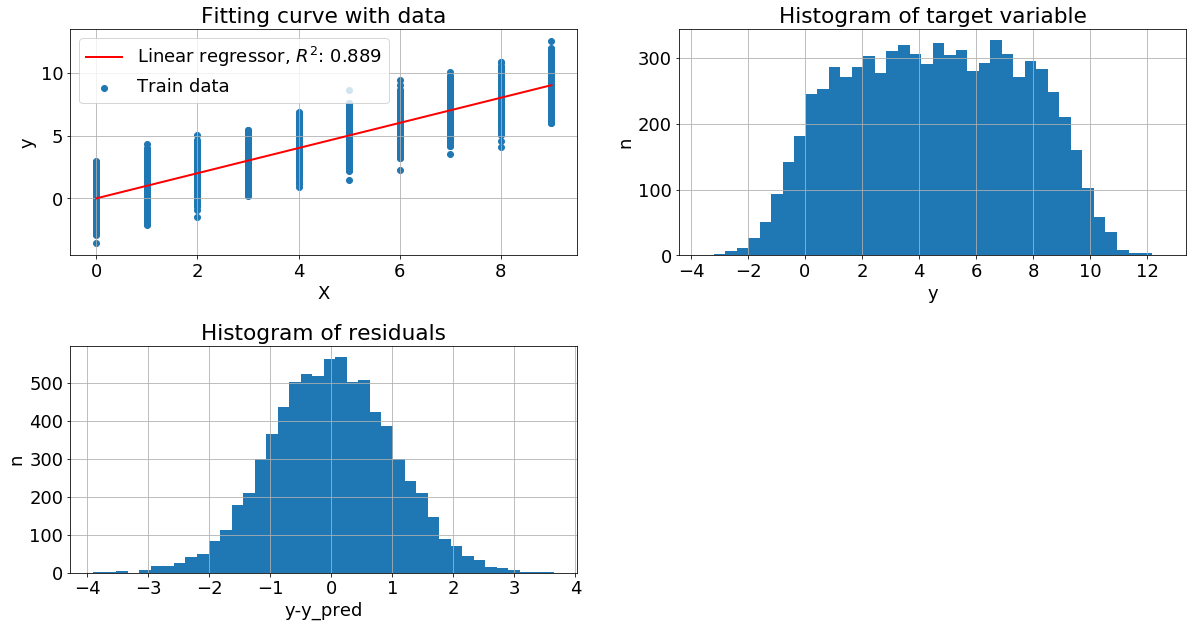
Нормальное распределение целевой переменной. Пусть x - случайное целое число из отрезка [0, 99], а y = x + N(0,1), где N(0,1) - нормальный шум с нулевым средним и стандартным отклонением равным 1.

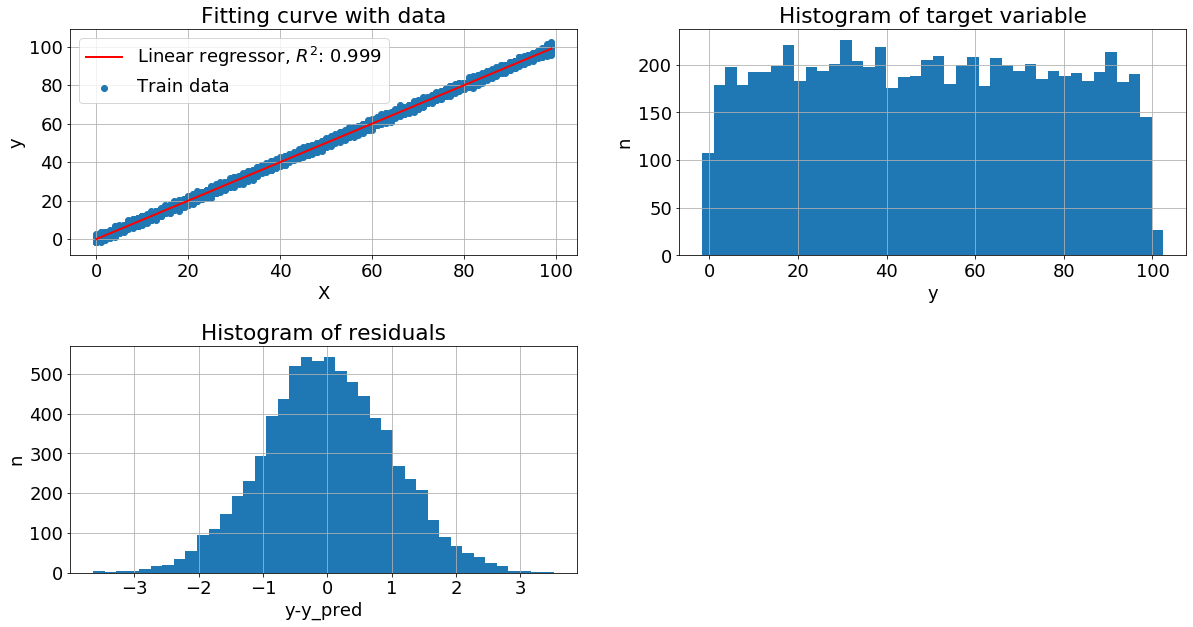
Видим, что у нас очень хорошая метрика качества на тестовых данных R^2 = 0.999 при этом целевая переменная более близка к равномерному распределению, чем к нормальному. А вот распределение остатков близко к нормальному.

Признак с пуассоновским распределением. Если признак x имеет пуссоновское распределение, а y = x + N(2,1), то распределение целевой переменной близко к нормальному, хотя и немножко смещенно, как и распределение остатков.

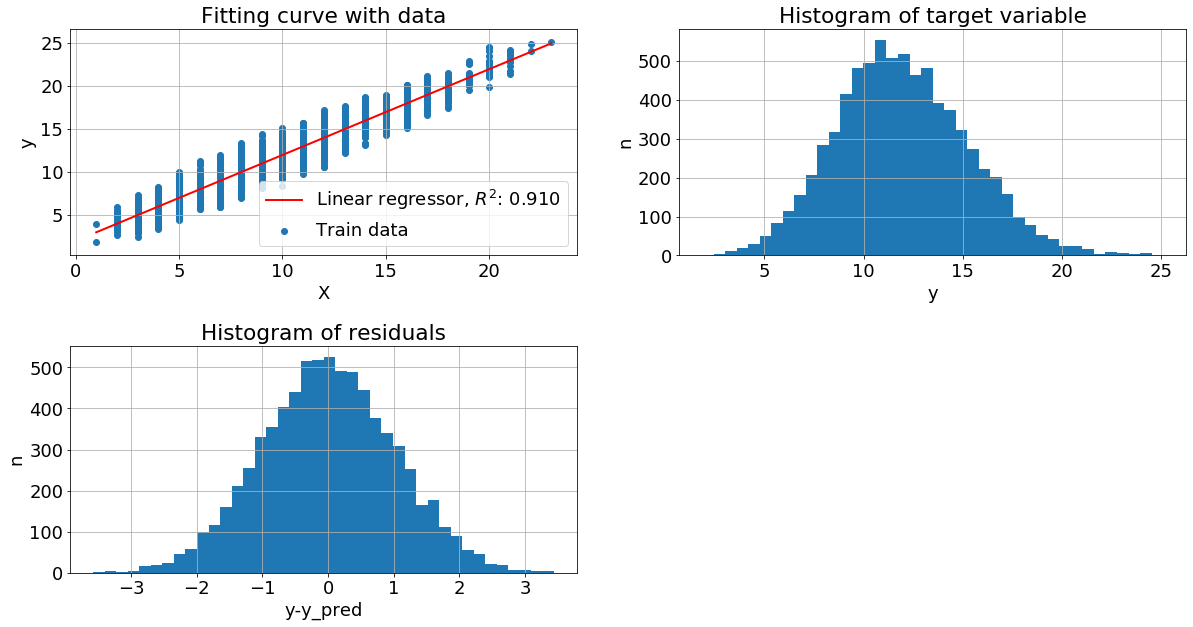
Целевая переменная с пуассоновским шумом. В следующем примере вместо гауссовского шума, мы добавим пуссоновский, при этом гистограмма остатков имеет смещенное распределение с длинным правым хвостом, но метрика качества высока. Можно объяснить это тем, что хвост имеет низкую вероятность и малое смещение не существенно для модели.

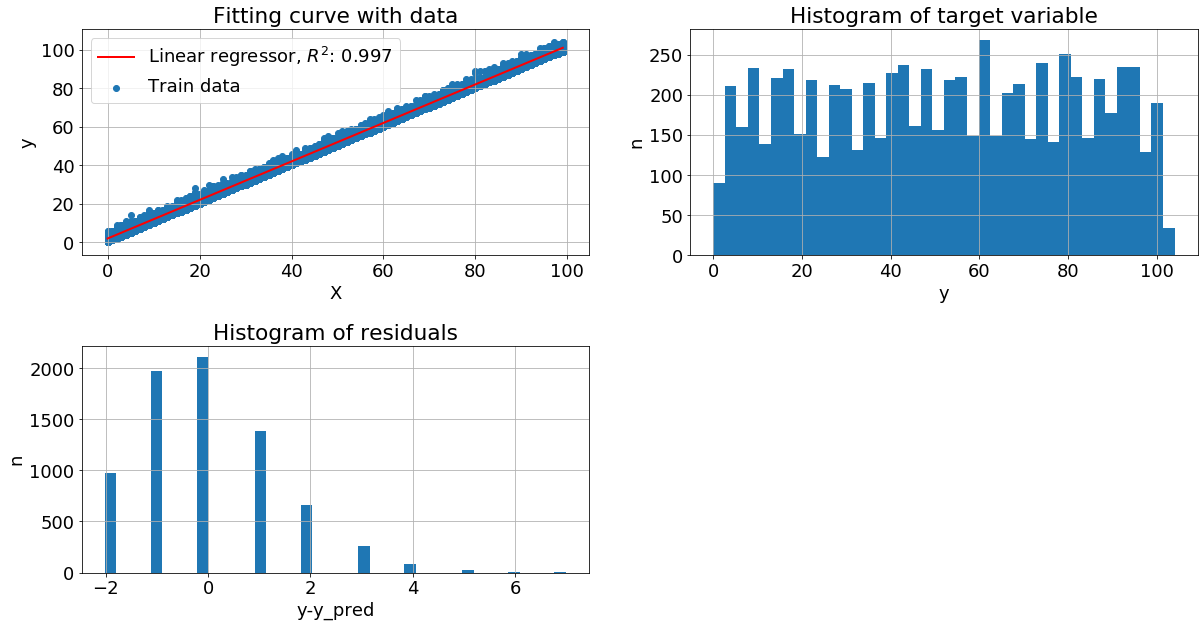
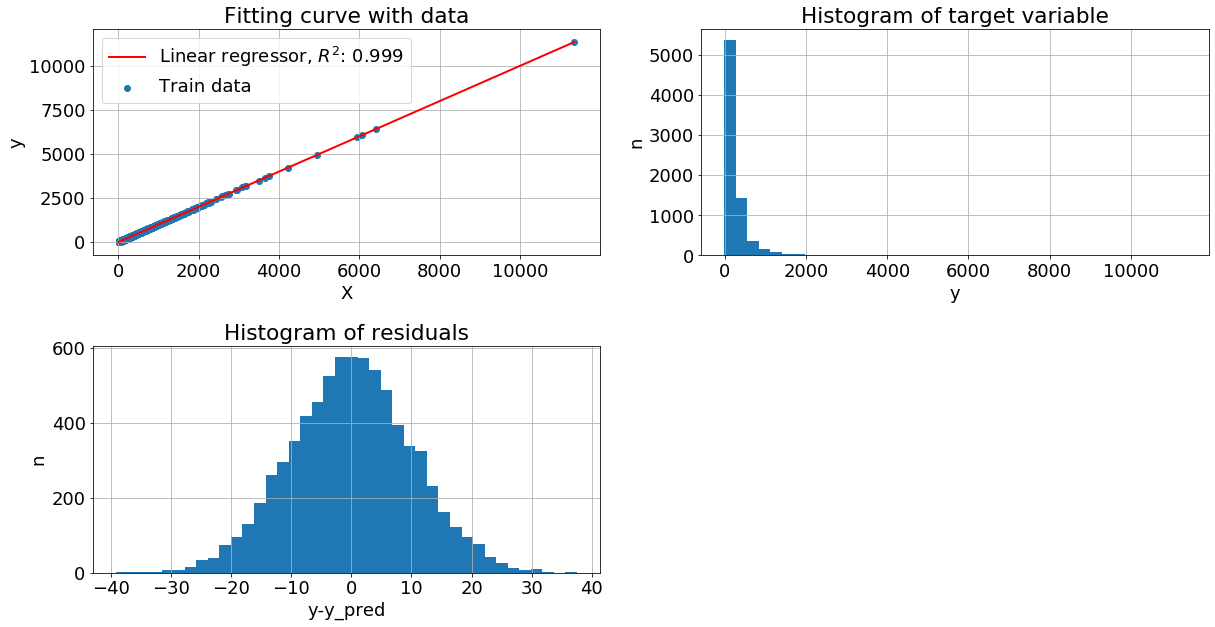
Целевая переменная зависит от признака по экспоненциальному закону. Пришло время существенно подпортить данные, пусть теперь y = exp(x+N(0,1)). Диаграмма остатков сильно смещена, метрика качества упала вниз.

Чтобы исправить ситуацию, можем прологарифмировать y и улучшить метрику:

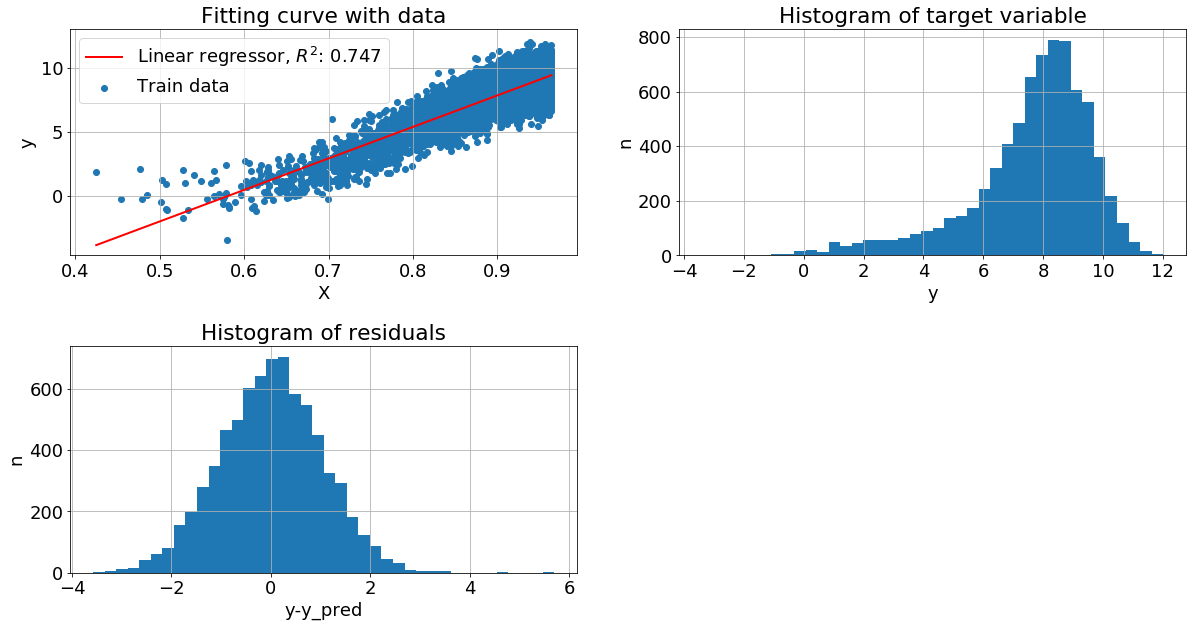
Признак имеет логнормальное распределение. Целевая переменная имеет вид y=x+N(0,10). В этом примере видим хорошее качество, но распределение целевой переменной сильно смещенно влево.

Целевая переменная распределена нормально, но с обратным средним. Здесь $y = N(10-\frac{1}{x+0.1}, 1)$

А теперь прологарифмируем y и видим, что метрика качества выросла, а остатки приблизились к нормальному распределению:

К целевой переменной прибавили Гамма-шум. Без преобразований метрика показывает не очень хорошее качество:

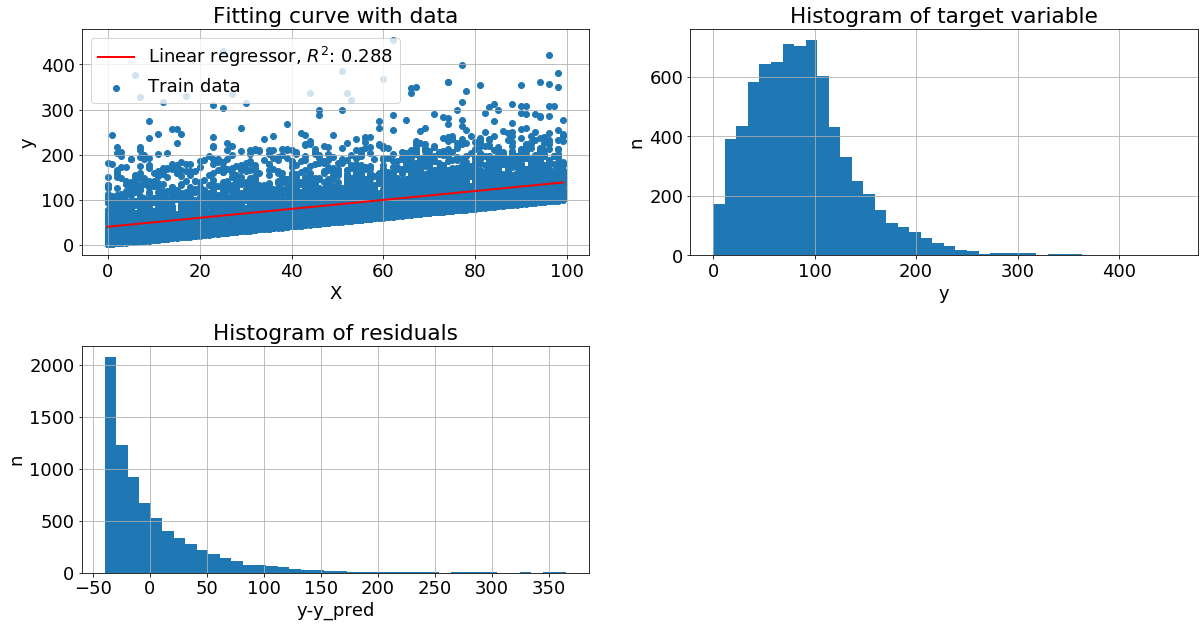
После преобразований метрика увеличилась на 34%:

У целевой переменной экспоненциальный шум. Без преобразований:

После преобразований метрика увеличилась:

Связь с рядами Тейлора

Мы видели, что преобразование целевой переменной работает хорошо, когда оно приводит к нормальному распределению в остатках или же является обратной функцией (если y=exp(1+x), то log(y) = 1+x). Можно ли как-то еще понять, какая функциональная зависимость есть между y и x?

Рассмотрим такую зависимость y=(X+1)^5 , без шума. Если мы добавим еще столбцы со степенями исходного признака: X^2, X^3, X^4, X^5 и передадим эти данные на вход линейной регрессии, то получим такие коэффициенты:

[5. 10. 10. 5. 1.]

Это не что иное, как коэффициенты соответствующего ряда Тейлора в данном случае можно просто расскрыть скобки по биному и получить тоже самое

Аналогично для $y=\sqrt{x+1}$ , при этом добавим чуть больше степеней, чтобы получить лучшую точность на первых пяти коэффициентах (сравните с настоящими коэф.):

[0.49999918 -0.12497953 0.06228674 -0.03788806 0.02348887 -0.01239518 0.004481 -0.00077948]

Если $y = \frac{1}{1+X}$ (сумма геометрической прогрессии), то получим такие коэффициенты:

[-0.99995384 0.99882878 -0.98761435 0.93032518 -0.76396752 0.47829397 -0.19124774 0.03533654]

Видим что первые 4 коэффициента довольно близки к реальным.

Но даже небольшое добавление шума сильно влияет на коэффициенты. Возьмем y=(x+1)^5 и добавим нормальный шум. Посмотрим, как меняется среднеквадратичная ошибка(MSE) определения коэффициентов (берем сумму квадратов разностей между реальными коэф. Тейлора и полученными коэф. линейной регрессии, а далее усредняем) в зависимости от параметра распределения $\sigma$ . Возьмем выборку в 100 тыс. точек.

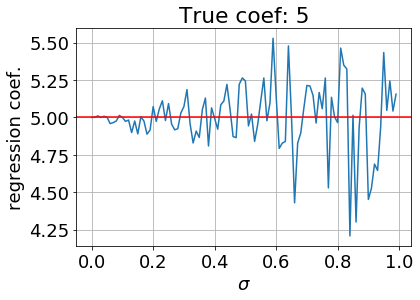
Видно, что даже в небольшем диапазоне изменения $\sigma$ - от 0 до 1.0, среднеквадратичная ошибка существенно возрастает. При этом коэффициенты регрессии все больше отклоняются от своих истинных значений, например, коэффициент при первой степени x:

Выводы

Распределение целевой переменной может быть не нормальным: смещенным, или равномерным. При этом будет хорошая метрика качества и никаких дополнительных преобразований не требуется.
Необходимо следить за распределением остатков и подбирать такое преобразование данных, чтобы это распределение стремилось к нормальному и тогда метрика будет расти.
Очень маловероятно, но все же - если удалось обнаружить какую-либо закономерность в коэффициентах регрессии, то можно попробовать соотнести с каким-нибудь из рядов Тейлора и прямо угадать функциональную зависимость между y и x.

Ноутбук с кодом можно скачать здесь.

Теги:

Хабы:

Машинное обучение

Преобразования целевой переменной в задачах линейной регрессии

Постановка задачи

Решение задачи

Различные модели порождения данных

Связь с рядами Тейлора

Выводы

Публикации

Истории

Работа

Ближайшие события