KeisN13 26 янв 2023 в 04:11

Выжимаем максимум из логики — сверхбыстрый, но прожорливый сумматор

9 мин

15K

FPGA*Высокая производительность*Ненормальное программирование*

ПЛИС-культ привет, FPGA хаб!

Давненько я не писал полноценных статей на хабре, всё больше как-то занимался организацией FPGA движа: всякими там новостными подборками, ютуб стримами по FPGA, организацией плисовых конференций и много чем другим.

Но всё новое — хорошо забытое старое, поэтому решил изложить в текстовом виде несколько идей, которые легли в основу стримов.

И в этой заметке предлагаю вам погрузиться в небольшое исследование c реализацией конвейеризованного многоразрядного сумматора всего с 1 уровнем логики, эдакого LUTа в сферическом вакууме, идеи которого, я уверен, найдут отклик в исследовательских работах начинающих адептов программируемой логики.

Очень коротко: теория и проблема переноса

Сумматоры делятся на два подвида, если так можно сказать. Это полусумматор и полный сумматор.

Полусумматор — комбинационная логическая схема, имеющая два входа и два выхода. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита s и c, где s — это бит суммы по модулю 2, а c — бит переноса.

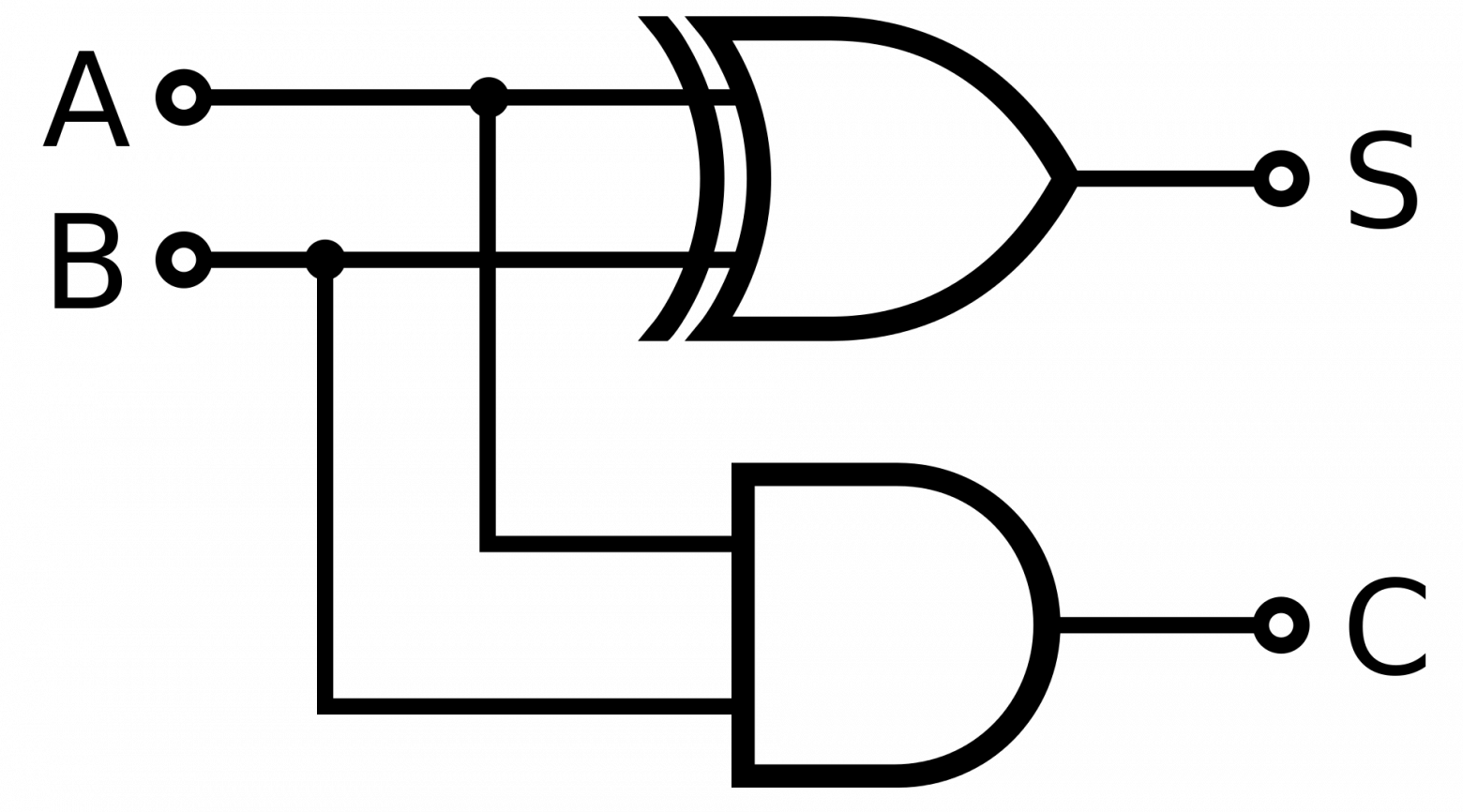
Конечно, складывать однобитные числа нам не особо интересно, куда больший интерес представляется в сложении многоразрядных чисел.

Для этого используют цепочку из полных сумматоров. При этом сам полный сумматор состоит из двух полусумматоров.

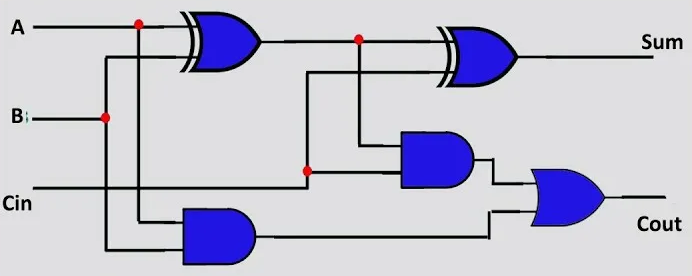
Соединяя полные сумматоры в цепочку, показанную на рисунке ниже, мы получим схему сложения многоразрядных чисел. Получается так называемый сумматор со сквозным переносом (Ripple Carry Adder)

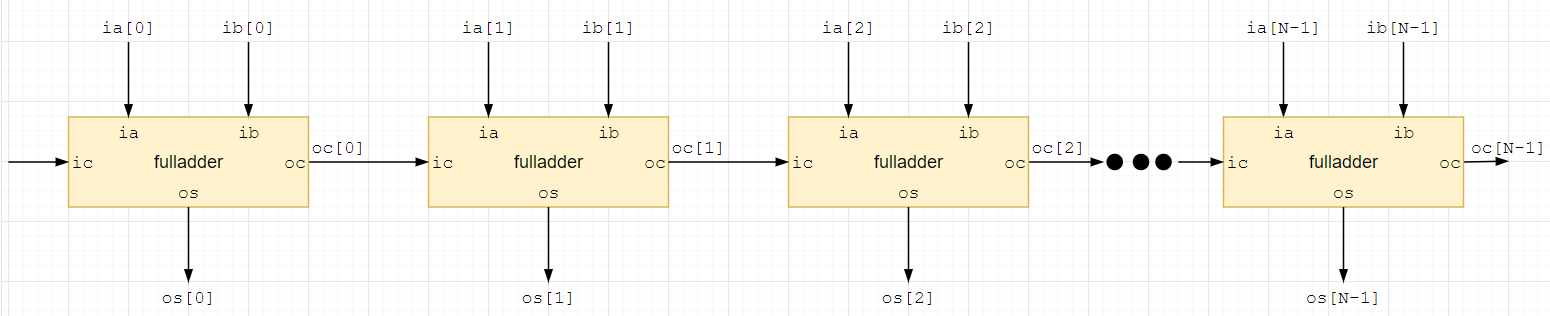
Погуглите, на самом деле, разных видов сумматоров есть значительное количество.

Переходим к фундаментальной проблеме.

Внимательный или знающий читатель, обратил внимание, что цепь переноса соединяется последовательно (выход переноса одного полного сумматора oc подключен ко входу переноса ic следующего полного сумматора). К чему это нас приводит?

Приводит это к тому, что цепь переноса становится самой длинной цепочкой в нашей схеме и чем больше разрядность операндов, тем длиннее эта цепочка. А как мы знаем, длинная цепочка логики (они же уровни логики) отрицательно сказывается на производительности схемы.

Если взять самый утрированный крайний случай, при котором у нас на один полный сумматор тратится 1 уровень логики, то для 8 битного сумматора будет 8 уровней логики. Если представить это в цифрах, то производительность нашей схемы упадет в несколько раз.

Поэтому в ПЛИС для выполнения операций с широкими данными используются специализированные ресурсы — такие как DSP-секции и специализированные цепи переноса (carry-chains — это специальный ресурс, имеющий значительно меньшую длину связей как раз для компенсации длинных цепей переноса)

Но, давайте пофантазируем: а что, если в нашей FPGA нет свободных DSP секций и цепи переноса не предусмотрены архитектурой ПЛИС (что крайне маловероятно для современных ПЛИС). Сколько бы ресурсов потребовалось на реализацию многоразрядного сумматора всего с одним уровнем логики?

В этой статье мы постараемся найти ответ на этот ~~жизненно важный~~ вопрос.

Формулируем задачи

В рамках статьи нам предстоит:

разработать схему многоразрядного сумматора с одним уровнем логики, т.е. максимально конвейеризированную версию.
Провести сравнительный анализ производительности и потребляемых ресурсов.

Дайте мне ведро регистров, и я конвейеризирую сумматор

Решая первую задачу, снова обратимся к схеме многоразрядного сумматора. Для простоты понимания возьмем 4-х разрядный сумматор.

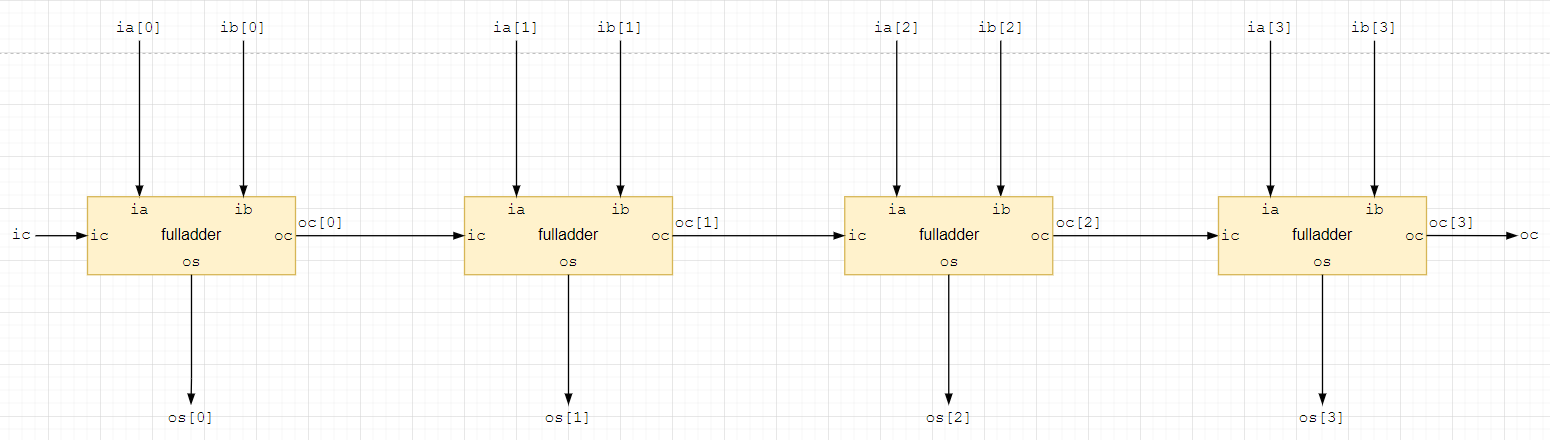
Далее следует ряд несложных умозаключений про задержки.

Если текстовая версия вам затруднительна для понимания, попробуйте посмотреть отрывок со стрима, где я пытался ее объяснить;
предположим мы хотим поставить регистр на выход переноса нулевого сумматора;
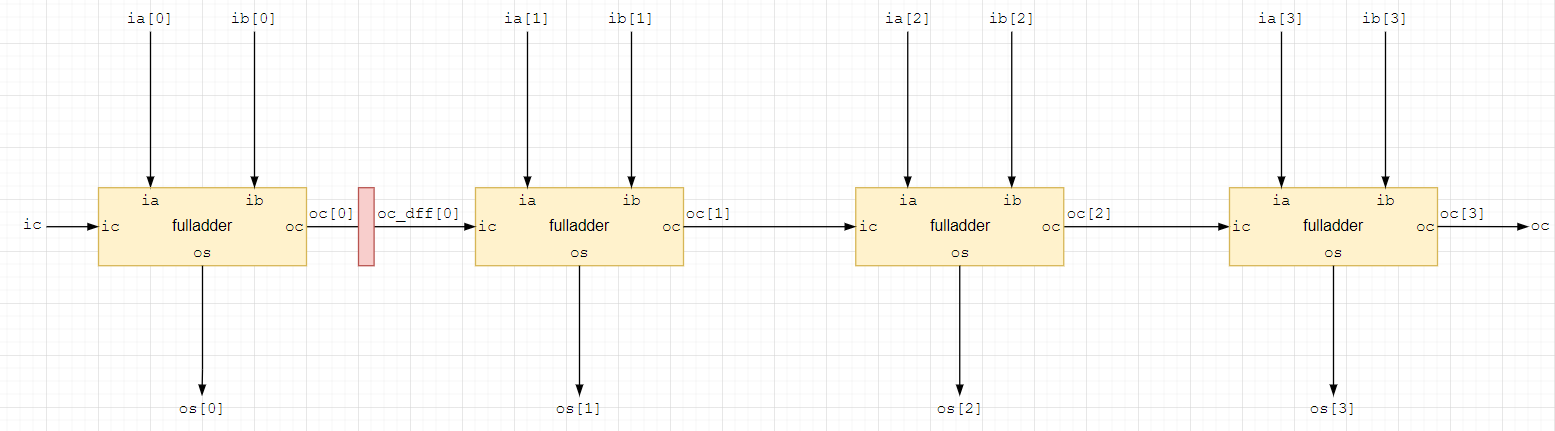
тогда и данные на входе первого сумматора ia[1] и ib[1] следует задержать на 1 такт;
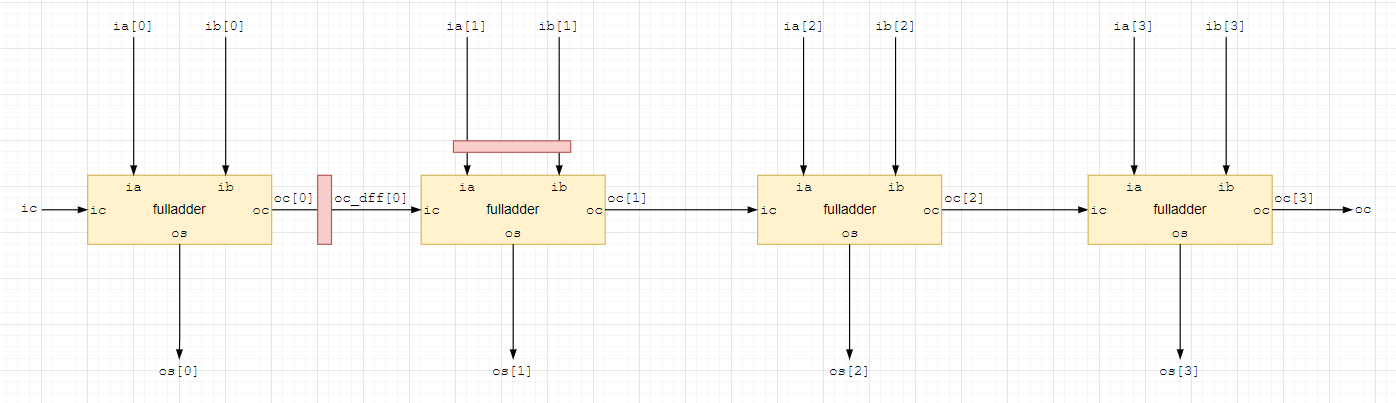
поставим триггер на выход переноса первого сумматора;
тогда с учетом задержки переноса нулевого сумматора данные на входе второго сумматора следует задержать на 2 такта;
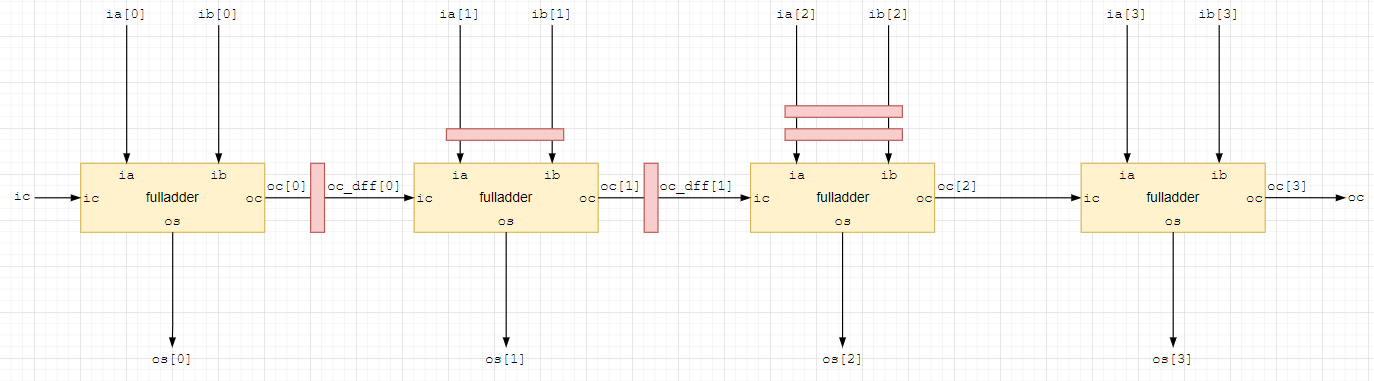
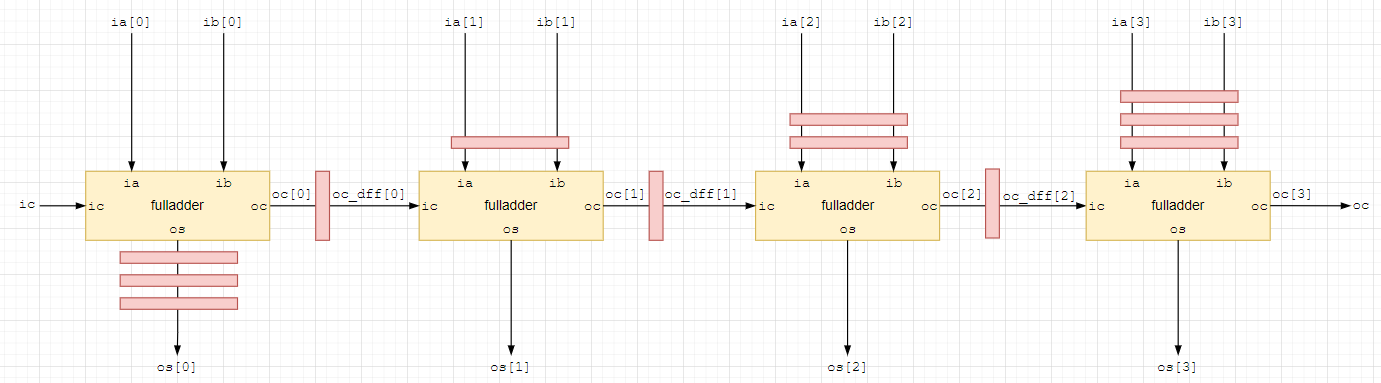
повторяя вставку регистров для остальных разрядов, получим следующую блок схему;
теперь разберемся с выходом суммы сумматоров os;
мы задержали входные данные на какое-то количество тактов, поэтому выход суммы каждого сумматора окажется задержанным на это количество тактов (нам же нужно получить корректные значения с выхода os каждого сумматора одновременно);
следовательно нужно компенсировать эту задержку с помощью регистров на выходе суммы каждого сумматора;
Ответим на вопрос: "На сколько тактов окажется задержан выход последнего сумматора по сравнению с нулевым?"
на три такта (именно на столько тактов мы задержали входные данные третьего сумматора);
Ставим задержку os[0] на три такта;
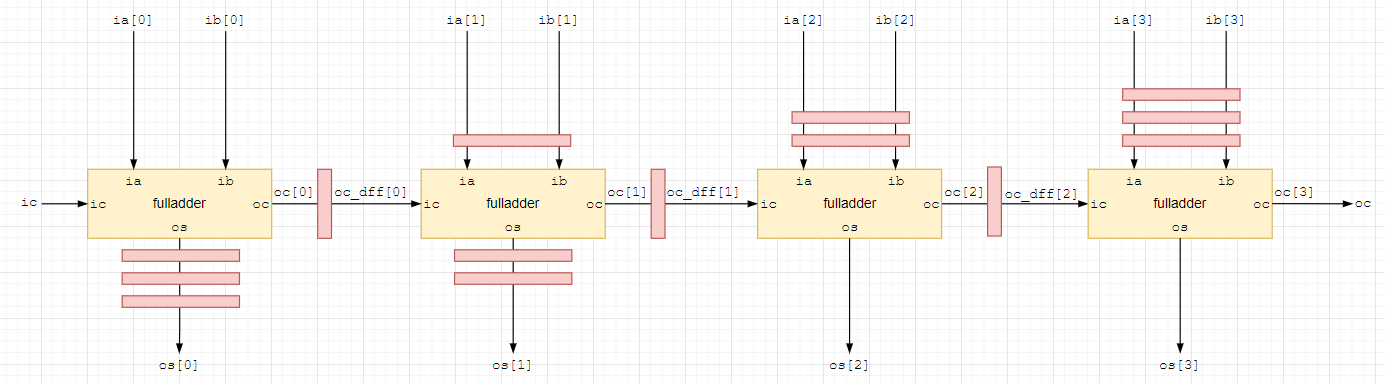
"На сколько тактов окажется задержан выход последнего сумматора по сравнению с первым?"
на два такта. Ставим задержку os[1] на два такта;
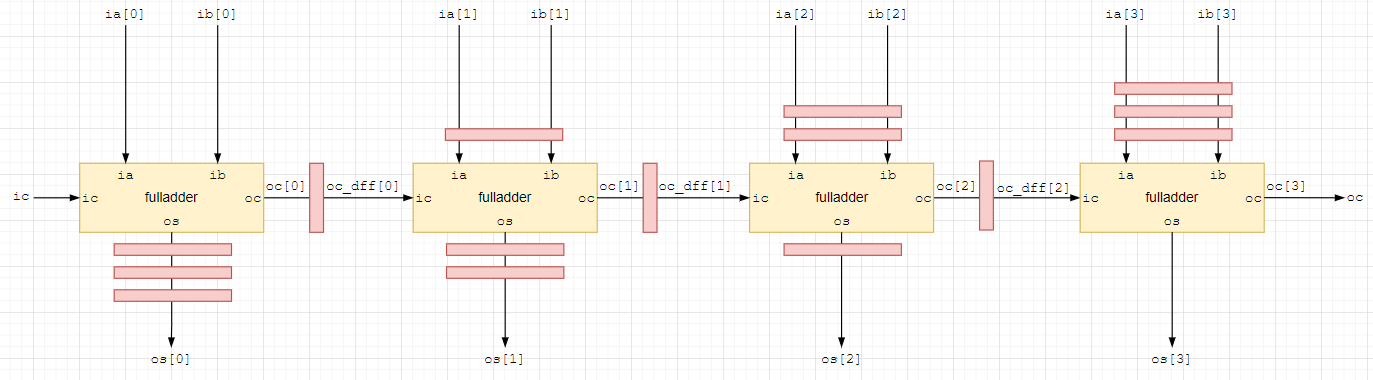
и тд.
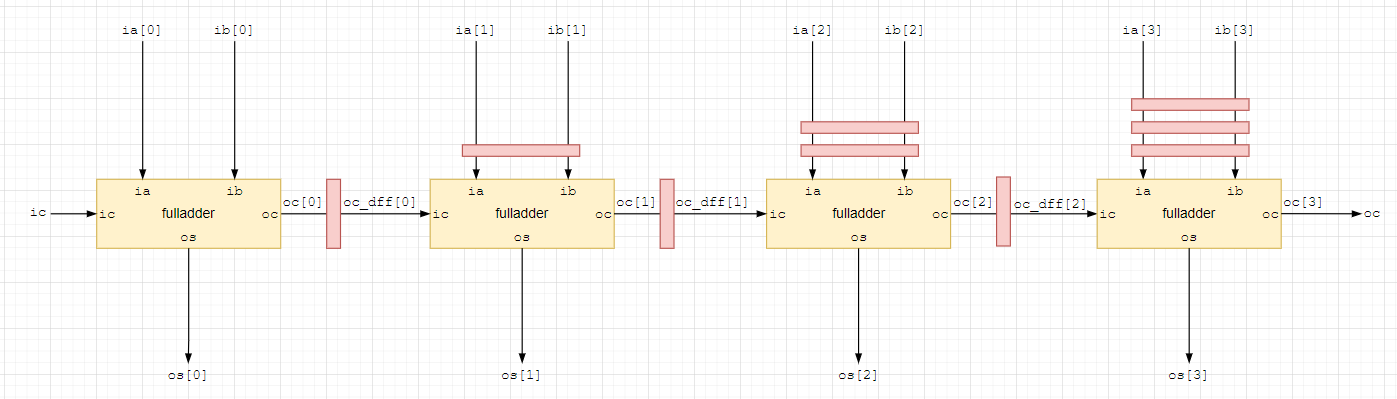
для полноты конвейеризации добавим еще один регистр к выходу переноса последнего сумматора и также не забудем ее учесть для всех входов ia, ib и выходов os.

В конечном итоге получаем схему конвейеризованного 4-х разрядного сумматора с одним уровнем логики

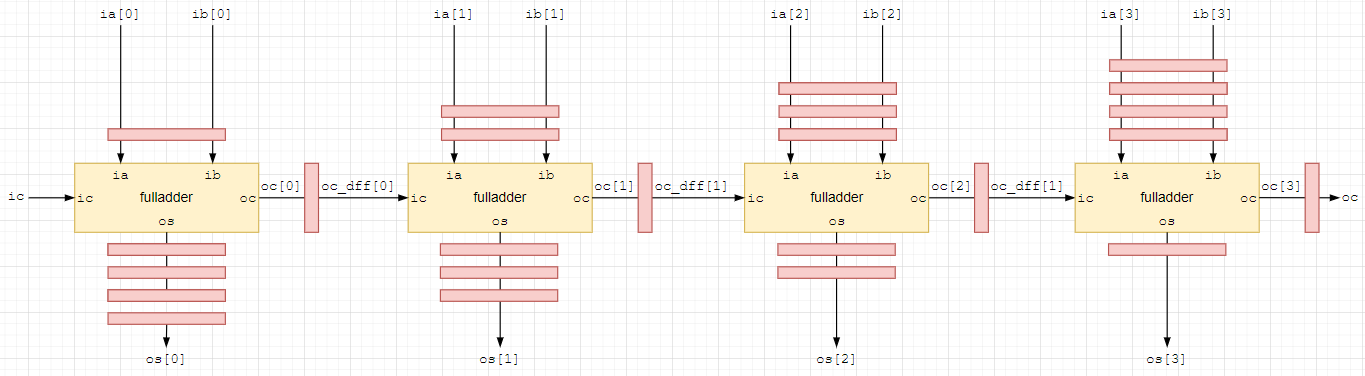
Приступаем к разработке кода

Проанализировав полученную блок-схему, приходим к выводу, что она может быть разбита на несколько сегментов fulladder_pipelined, каждый из которых состоит из полного сумматора fuladder и нескольких линий задержки (показанных прямоугольниками c заливкой цвета #F8CECC).

Для начала опишем полный сумматор fulladder. Его код крайне прост, а варианты реализации могут быть разные. Приведу один из них:

module fulladder(
    input  ia, ib, ic,
    output  os, oc
);

    assign os  = (ia ^ ib) ^ ic;

    assign oc = (ia & ib) | (ib & ic) | (ic & ia);

endmodule

Здесь

ia — первый операнд
ib — второй операнд
ic — вход цепи переноса
os — выход суммы
oc — выход переноса
Проверим нашу схему в elaborated представлении и после синтеза

Как видим, мы получили две LUT, т.е. для реализации полного сумматора потребовался 1 уровень логики (LUT стоят параллельно, и выход первой не связан со входами второй, как и выход второй не связан с выходом первой)

Маленькое отступление: в зависимости от выбранной FPGA по время мапинга две LUT могут быть упакованы в одну. Такое, например, наблюдается для ПЛИС Xilinx 7-ой серии. В ПЛИС этой серии LUT имеют дополнительный выход. Но сильно сути то не меняет — у нас по-прежнему будет 1 уровень логики. Такая упаковка лишь скажется на потребляемых ресурсах.

Как вы понимаете линия задержки — это ни что иное как обычный сдвиговый регистр, который в современных FPGA может быть реализован как на отдельно взятых триггерах, так и на специализированном аппаратном ресурсе сдвигового регистра. Про это есть отдельное видео, рекомендую ознакомиться при желании.

Код для линии задержки я взял из стандартного шаблона Vivado (Tools — Language templates — Verilog — Synthesis Constructs — Coding Examples — Shift Registers — SRL — Static Shift SRL (single bit)) и немного его модифицировал.

Параметр C_CLOCK_CYCLES задает задержку на указанное количество тактов. В данной реализации C_CLOCK_CYCLES может принимать значения от 1.
Назначение сигналов:

id — вход данных линии задержки
iclk — вход тактового сигнала
oq — выход линии задержки

module delay
#( parameter C_CLOCK_CYCLES = 4)
(
    input id, iclk,
    output oq
);

    wire data_in;
    wire data_out;

    reg [C_CLOCK_CYCLES-1:0] shift_reg = {C_CLOCK_CYCLES{1'b0}};

    assign data_in = id;

    always @(posedge iclk)
         shift_reg <= {shift_reg[C_CLOCK_CYCLES-1:0], data_in};

    assign oq = shift_reg[C_CLOCK_CYCLES-1];

endmodule

Далее объединяем полный сумматор fulladder с линиями задержки delay и получаем fulladder_pipelined со следующими портами:

ia — первый операнд
ib — второй операнд
ic — вход цепи переноса
iclk — вход тактового сигнала для линий задержки
os — выход суммы
oc — выход переноса

Поскольку длина линии задержки будет меняться от сегмента к сегменту, вынесем её в качестве параметров:

C_INPUT_DELAY — длина линии задержки по входам ia и ib
C_OUTPUT_DELAY — длина линии задержки по выходу os

module fulladder_pipelined
#( 
    parameter C_INPUT_DELAY  = 3,
    parameter C_OUTPUT_DELAY = 2
)
(
    input ia, ib,
    input ic,
    input iclk,
    output os,
    output oc
);

    wire  a_dff, b_dff, fa_os, fa_oc ;

    delay #(C_INPUT_DELAY) delay_ia(ia, iclk, a_dff);
    delay #(C_INPUT_DELAY) delay_ib(ib, iclk, b_dff);

    fulladder fa (a_dff, b_dff, ic, fa_os, fa_oc);

    delay #(C_OUTPUT_DELAY) delay_os(fa_os, iclk, os);
    delay #(1)              delay_oc(fa_oc, iclk, oc);

endmodule

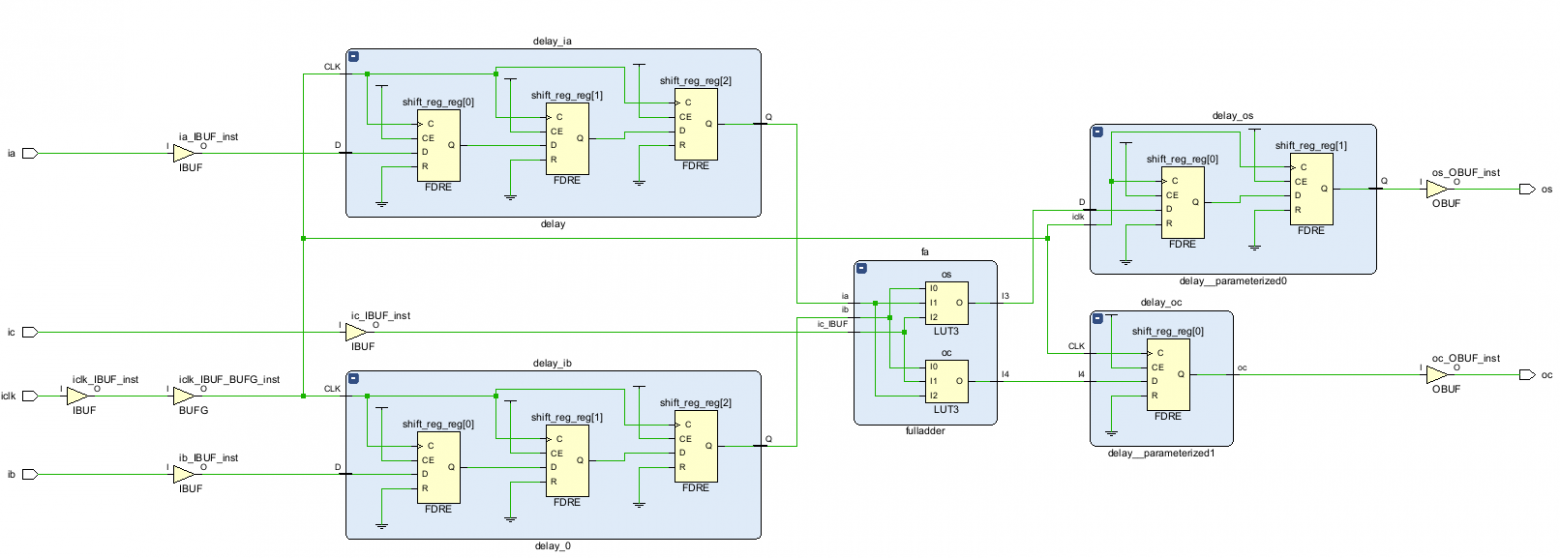
Теперь нам остается только последовательно соединить несколько сегментов fulladder_pipelined с помощью конструкции generate.

Количество таких сегментов будет определяться ни чем иным как разрядностью входных операндов ia и ib, которую мы зададим с помощью параметра C_OPERAND_WIDTH.

Единственный нюанс, который я так и не придумал как обойти для написания однострочного generate, это подключение нулевого сегмента для разрядов ia[0] и ib[0], в котором вход переноса подключается наружу (который с большой вероятностью будет просто сажаться в '0' при использовании в проекте, но для пущей универсальности я просто вывел его наружу), поэтому использовал оператор if.

module adder_pipelined_h
#( parameter C_OPERAND_WIDTH = 4)
(
    input [C_OPERAND_WIDTH - 1 : 0] ia, ib,
    input ic,
    input iclk,
    output [C_OPERAND_WIDTH - 1 : 0] os,
    output oc
);

    wire [C_OPERAND_WIDTH - 1 : 0] fap_oc;

    genvar i;
    generate
        for (i=0; i < C_OPERAND_WIDTH; i=i+1)
        begin: fa

            if (i==0) 
                fulladder_pipelined  #(i+1, C_OPERAND_WIDTH - i) fap(ia[i], ib[i], ic, iclk, os[i], fap_oc[i]);
            else
                fulladder_pipelined  #(i+1, C_OPERAND_WIDTH - i) fap(ia[i], ib[i], fap_oc[i-1], iclk, os[i], fap_oc[i]);
        end
    endgenerate

    assign oc = fap_oc[C_OPERAND_WIDTH - 1];

endmodule

Я использовал здесь позиционное назначение параметров и портов, поскольку их мало в этом проекте и они по иерархии везде одинаковые. Старайтесь так не делать и отдайте предпочтение именованному присвоению :)

Теперь дело за малым.

Я надеюсь вы потратили 15 минут на просмотр видео про сдвиговые регистры и теперь знаете, что для запрещения инкапсуляции триггеров в аппаратный ресурс вам надо открыть настройки синтеза и поставить галочку -no_srlextract (применительно к Vivado). Сделано это для того, чтобы оценить сколько регистров будет задействовано в нашем проекте, хотя это и не сложно просто посчитать. Какая-никакая арифметическая прогрессия тут есть.
В дальнейшем при оценке ресурсов я разрешу вставку ресурсов, просто для полноты анализа потребляемых ресурсов.

Для того, чтобы проверить корректность написанного, я запустил синтез для 4-х разрядного конвейеризированного сумматора и получил соответствующий блок-схеме результат.

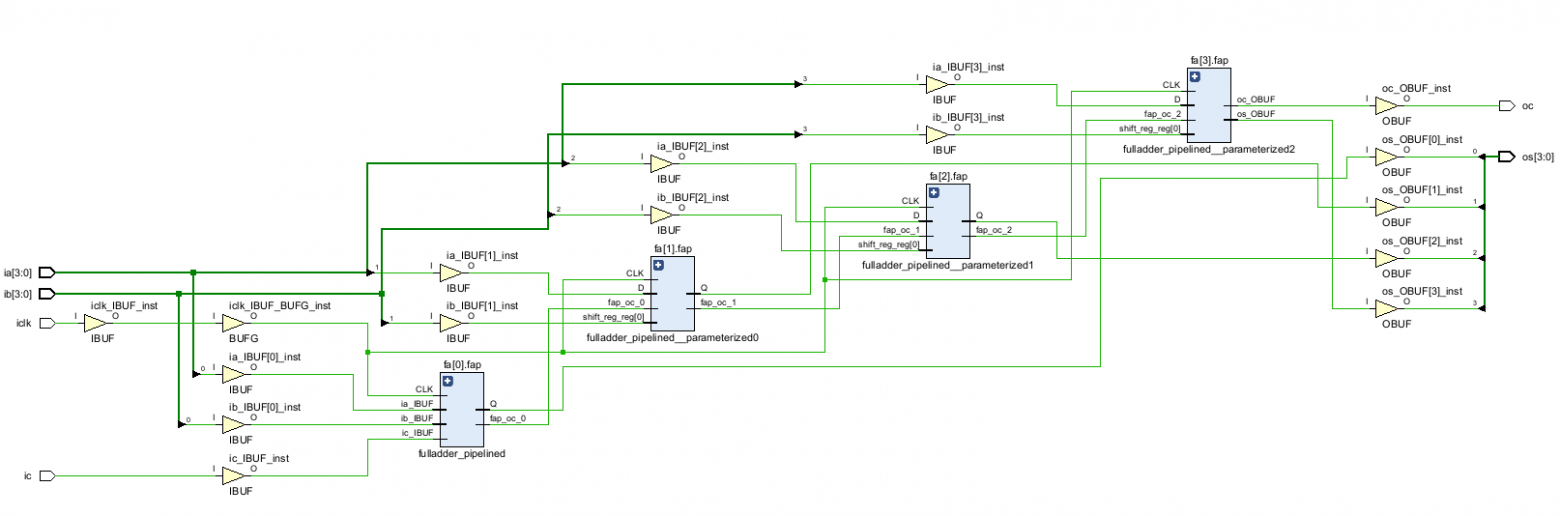
Я не буду здесь приводить тестбенч, для моделирования, оставлю этот занимательный этап верификации читателю в качестве факультативного задания.

Оценка занимаемых ресурсов и производительности

Сравнительный анализ мы проведем для 64-х разрядных сумматоров и трех случаев:

сумматор, реализованный с помощью поведенческого описания:

module adder
#( parameter C_OPERAND_WIDTH = 64)
(
input [C_OPERAND_WIDTH - 1 : 0] a, b,
input iclk,
output reg [C_OPERAND_WIDTH : 0] r
);
reg [C_OPERAND_WIDTH : 0] r_i;
reg [C_OPERAND_WIDTH - 1 : 0] a_i, b_i;

always @(posedge iclk)
begin
    a_i <= a;
    b_i <= b;
    r <= a_i + b_i;
end
endmodule

конвейеризованный сумматор без вставки аппаратных сдвиговых регистров;
конвейеризованный сумматор с использованием аппаратных сдвиговых регистров.

Анализ проведем для микросхемы xc7a35tcsg324-1, установленной на моей любимой отладке Arty A35-T в среде Vivado. Однако для анализа может быть выбрана абсолютно любая микросхема ПЛИС, в любой другой среде разработки.

Зададим всего одно проектное ограничение на тактовую частоту, которую установим равной 500МГц.

create_clock -period 2.000 -name iclk -waveform {0.000 1.000} [get_ports iclk]

Также на забываем запретить среде использование DSP секций (Synthesis settings — -max_dsp 0).

Для анализа я сделал три отдельных настройки запуска (design runs), по одному для каждого варианта.

Сравнительная таблица результатов показана ниже:

Обсудим результат

Из таблицы мы видим, что общим у нас является нарушение по ширине тактового сигнала. Это ограничение выбранной микросхемы, которая не может работать на таких частотах, но для нас этот параметр не является критичным в данном случае.

По сравнению частот работы реализованных сумматоров видим, что поведенчески описанный сумматор не может работать на заданной частоте (у него слишком много уровней логики, вызванной длинной цепью переноса), при этом временной анализ конвейеризованного сумматора показывает, что 500МГц для него не предел и он может быть работоспособен и на больших частотах.

По затрачиваемым ресурсам видим многократное превосходство поведенчески описанного сумматора. Что вполне объяснимо, ведь дополнительные оптимизации и использование цепей переноса были разрешены.

Разрешение использования аппаратных сдвиговых регистров значительно влияет на количество используемых ресурсов, но при этом проект развелся с несколько меньшей рабочей частотой. Увеличение количество LUT обусловлено тем, что аппаратный сдвиговый регистр в Xilinx 7-series является частью LUT.

Не следует забывать, что конвейер всегда добавляет латентность на получение данных. В случае простого сумматора она будет 1 такт, а в случае конвейеризованной версии — несколько таков. Сколько именно — зависит от разрядности данных. Но это обычная ситуация, когда мы жертвуем латентностью для получения более высокой тактовой частоты проекта.

Выводы, итоги, заключение

Сегодня сложно представить проекты, которые бы обходились без использования математических операций. Даже банальное обращение к памяти требует инкремента адреса.

Проанализированный полностью конвейеризованный сумматор в ряд ли найдет свое практическое применение, он больше создан в исследовательский целях. Задача конвейеризации стандартных операций (сложения, умножения, сравнения и тд) может послужить прекрасной темой для бакалаврской, дипломной или магистерской работы.

При этом, исходный модуль не сложно переделать таким образом, чтобы конвейер был не на каждом разряде, а, например, на каждые 5 разрядов. В таком случае мы сможем повысить тактовую частоту проекта и не сильно просесть по ресурсам ПЛИС. И уже такое применение вполне возможно в реальных проектах. Если этот пост наберёт 100+ стрелок вверх, я выложу исходники такого сумматора :)

Ну а для тех кто хочет посмотреть 3-х часовую видео версию перед сном приглашаю на Youtube.

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку