Привет, Хабр!
Меня зовут Марко, я работаю в Badoo в команде «Платформа». Не так давно на GopherCon Russia 2018 я рассказывал, как работать с координатами. Для тех, кто не любит смотреть видео (и всех интересующихся, конечно), публикую текстовый вариант своего доклада.
Сейчас у большинства людей в мире есть смартфон с постоянным доступом в Интернет. Если говорить в цифрах, то в 2018 году смартфон будет у почти 5 млрд людей, и 60% из них пользуются мобильным Интернетом.
Это огромные числа. Компаниям получать координаты пользователей стало легко и просто. Эти лёгкость и доступность породили (и продолжают порождать) огромное количество сервисов, основанных на координатах.
Всем нам известны компании типа Uber, игры, покорившие мир, такие как Ingress и Pokemon Go. Да что уж там, в любом банковском приложении есть возможность увидеть банкоматы или скидки поблизости.
Мы в Badoo также очень активно используем координаты, чтобы предоставлять своим пользователям лучший, актуальный и интересный для них сервис. Но о каком именно использовании идёт речь? Давайте посмотрим на примеры сервисов, которые у нас есть.
Badoo — это в первую очередь дейтинг. Место, где люди знакомятся друг с другом. Одним из важных критериев при поиске людей является расстояние. Ведь в большинстве случаев девушке из Москвы хочется познакомиться с мальчиком, который находится в паре километров от неё или по крайней мере тоже живёт в Москве, а не в далёком Владивостоке.
Сервисы, которые подбирают вам людей для «игры» «Да/нет» или показывают пользователей вокруг, занимаются поиском людей с подходящими вам критериями в каком-то радиусе от вас.
Для того чтобы ответить на вопросы, в каком городе находится пользователь, в какой стране или, ещё более точно, к примеру, в каком аэропорту или в каком университете, мы используем сервис Geoborder, который занимается так называемым geofencing-ом.
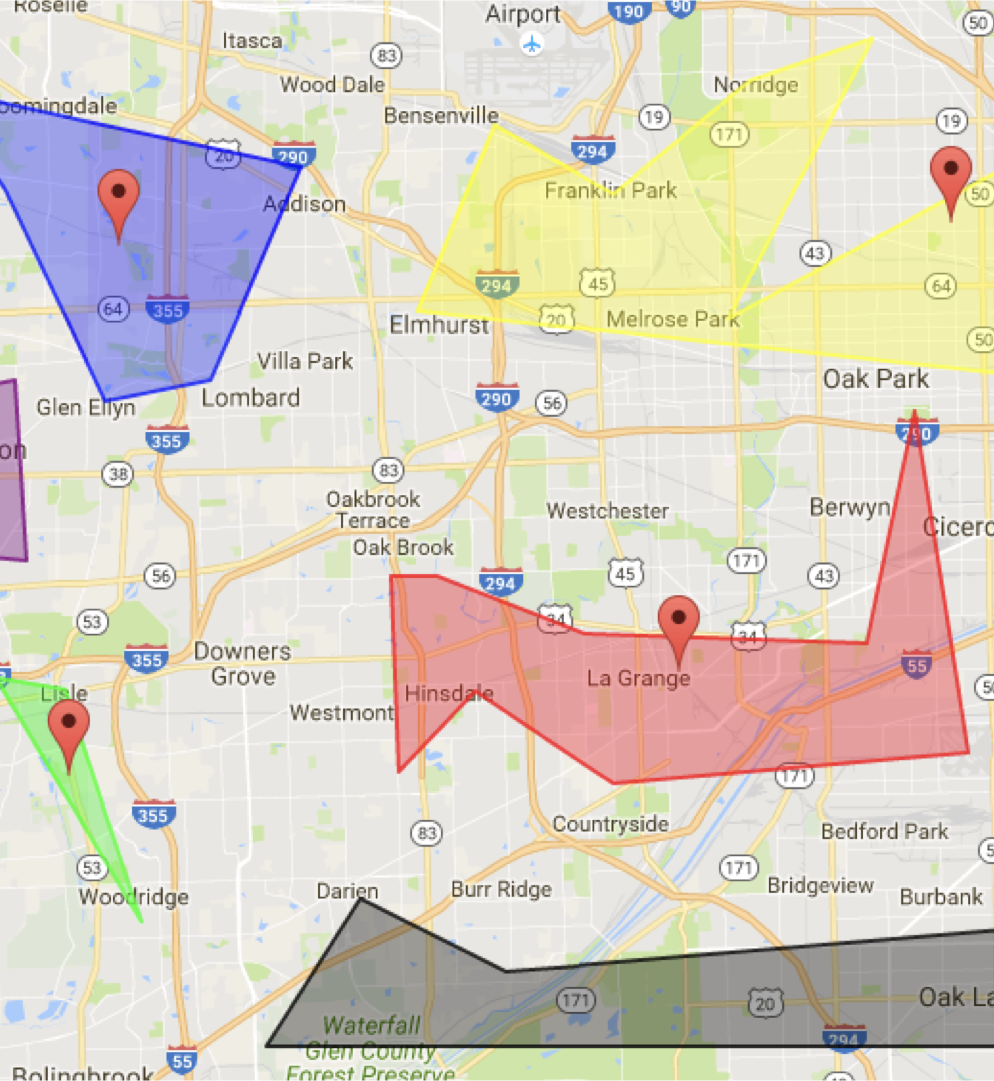
Самым простым способом ответить на эти вопросы было бы считать расстояние от пользователя до центра города или центра университета, но этот подход очень неточен и зависит от большого количества граничных условий.
Поэтому у нас расчерчены очень точные границы стран, городов, важных объектов (например, университетов и аэропортов, о которых я говорил). Эти границы задаются полигонами. Имея набор таких границ, мы можем понять, находится ли пользователь внутри полигона, или найти ближайший к нему полигон. Соответственно, мы можем сказать, в каком он городе, или найти ближайший к нему город.
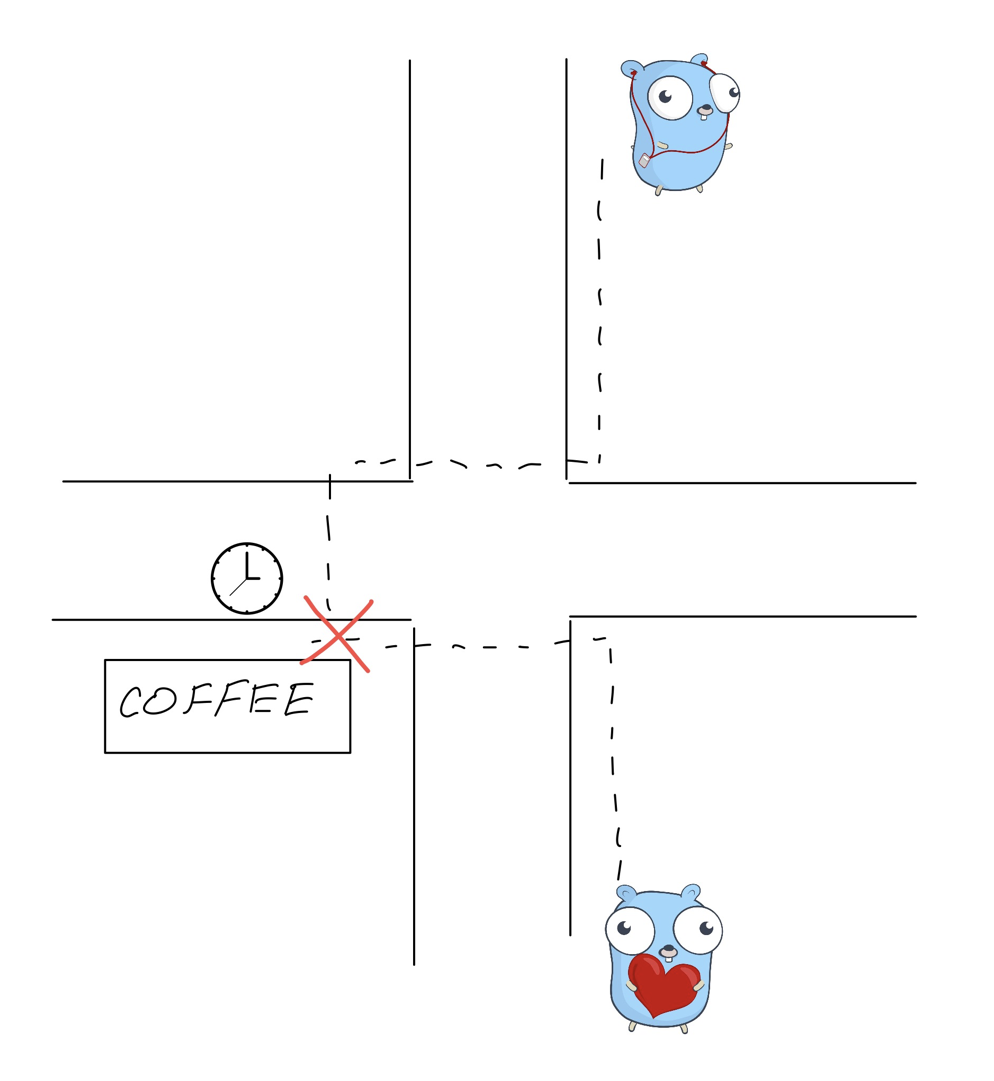
У нас есть очень популярная фича под названием Bumped Into, которая в фоновом режиме постоянно ищет пересечения пользователей во времени и в пространстве и показывает вам, что вот с этим мальчиком или с этой девушкой вы регулярно бываете в одном месте в одно и то же время или регулярно ходите одной дорогой. Эта фича очень нравится пользователям, поскольку является ещё одним поводом познакомиться и темой, с которой можно начать разговор.
Ну и последний пример, о котором я упомяну, связан с кешированием гео-информации. Представьте себе, что вы используете данные из, например, Booking.com, который предоставляет вам информацию о гостиницах вокруг, но лезть в Booking.com каждый раз — слишком долго. Ваша труба в Интернет, возможно, довольно узкая, как яма у этого гофера. Возможно, сервис, в который вы идёте за данными, берёт деньги за каждый запрос, и вам хочется немного сэкономить.

В этом случае неплохо бы иметь кеширующий слой, который заметно уменьшит количество запросов в медленный или дорогой сервис, а наружу будет предоставлять очень похожий API. Сервис, который будет понимать, что обо всех или о большинстве гостиниц в данной области он уже знает, эти данные относительно свежи, и, соответственно, можно не лезть за ними во внешний сервис. Такого рода задачи у нас решаются сервисом под названием Geocache.
Мы с вами уже поняли, что координат много, координаты — это важно, и на основе них можно сделать очень много интересных сервисов. Ну и что дальше? В чём, собственно, дело? Чем координаты отличаются от любой другой информации, полученной от пользователя?
А особенностей, я бы сказал, две.
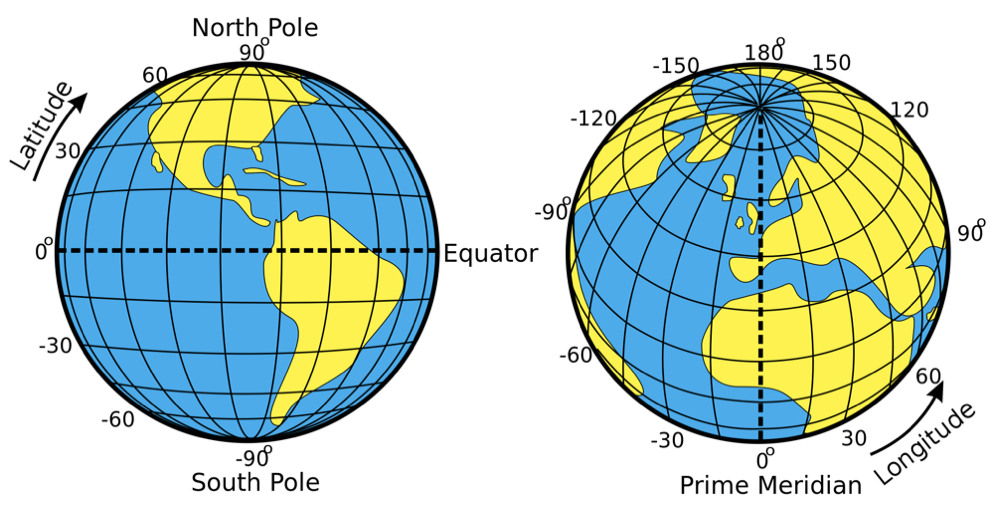
Во-первых, гео-данные трёхмерны, а точнее двумерны, так как в общем случае нас не интересует высота. Они состоят из широты и долготы, и поиск чаще всего идёт одновременно по обеим. Представьте себе поиск в какой-либо области. Стандартные индексы в распространённых СУБД неоптимальны для такого использования.
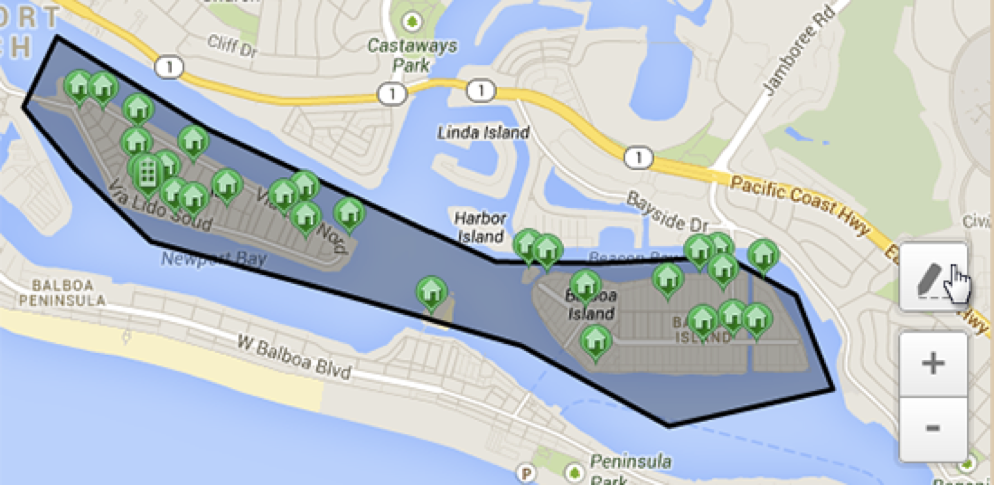
Во-вторых, многие задачи требуют более сложных типов данных типа полигонов, о которых мы говорили выше на примере сервиса Geoborder в Badoo. Полигоны, конечно, состоят из координат вершин, но требуют дополнительной обработки, и поисковые запросы на таких типах данных тоже сложнее. Мы уже видели запросы «Найти ближайший полигон к точке» или «Найти полигон, который включает данную точку».
Для того чтобы соответствовать этим особенностям, многие СУБД включают в поставку специальные индексы, заточенные под многомерные данные, и дополнительные функции, которые позволяют работать с такими объектами, как полигоны или ломаные.
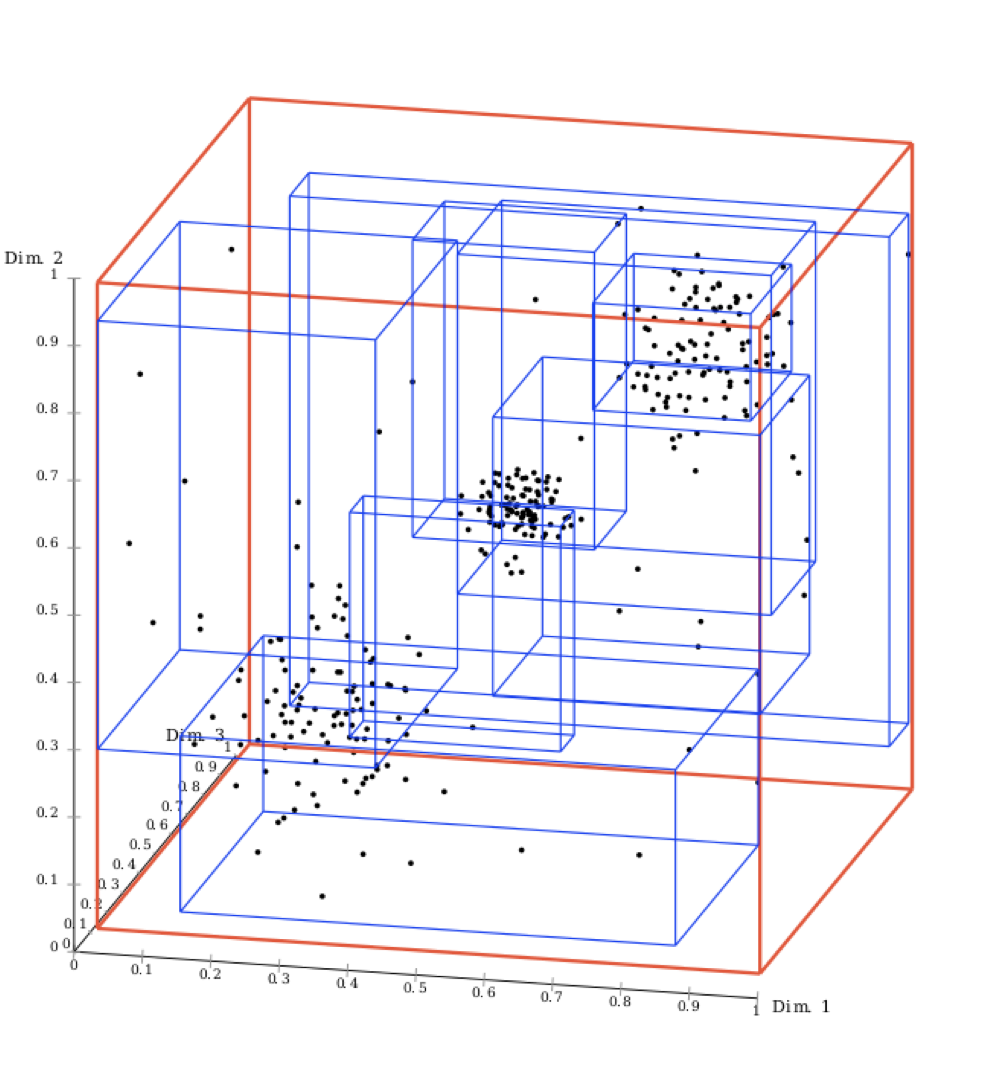
Наверное, самым ярким примером является PostGIS — расширение к популярной СУБД PostgreSQL, обладающее широчайшими возможностями для работы с координатами и географией.
Но использовать готовую СУБД — не единственное и не всегда лучшее решение.

Если вы не хотите делить бизнес-логику вашего сервиса между ним и СУБД, если вы хотите чего-то, что недоступно в СУБД, если вы хотите полноценно управлять вашим сервисом и не быть ограниченным возможностями масштабирования какой-либо СУБД, например, то вы можете захотеть встроить возможности поиска и работы с geo-данными в свой сервис.
Такой подход, бесспорно, гибче, но может быть и значительно сложнее, потому что СУБД — это решение формата «всё в одном», и многие инфраструктурные вещи типа репликации уже сделаны за вас. Репликации и, собственно, алгоритмов и индексов для работы с координатами.
Но не всё так страшно. Я хотел бы познакомить вас с библиотекой, которая реализует большую часть из того, что вам понадобится. Которая является своеобразным кубиком, легко встраиваемым везде, где вам нужно работать с геометрией на сфере или искать по координатам. С библиотекой под названием S2.
S2 — библиотека для работы с геометрией (в том числе на сфере), предоставляющая очень удобные возможности для создания geo-индексов.
До недавнего времени S2 была практически неизвестна и обладала совсем скудной документацией, но не так давно Google решила "перевыпустить" её в open-source, дополнив выкладку обещанием поддерживать и развивать продукт.
Главная версия библиотеки написана на C++ и имеет несколько официальных портов или версий на других языках, включая Go-версию. Go-версия на сегодняшний день не на 100% реализует всё то, что есть в C++-версии, но того, что есть, достаточно для реализации большинства вещей.
Помимо Google, библиотеку активно используют в таких компаниях, как Foursquare, Uber, Yelp, ну и Badoo, конечно. А среди продуктов, использующих библиотеку внутри, можно выделить всем вам известную MongoDB.
Но пока я не сказал ничего дельного о том, почему именно S2 удобна и почему позволяет легко писать сервисы c geo-поиском. Давайте я исправлюсь и немного погружусь во внутренности, прежде чем мы рассмотрим два примера.
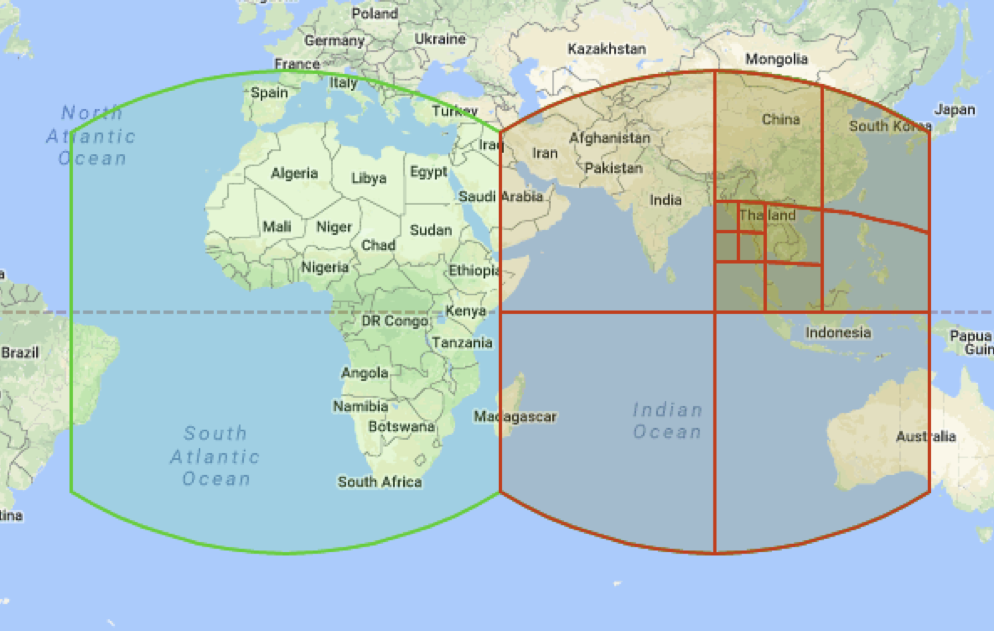
Обычно география подразумевает использование одной из распространённых проекций земного шара на плоскость. Например, всем нам известной проекции Меркатора. Недостаток такого подхода заключается в том, что любая проекция так или иначе имеет искажения. Наш с вами земной шар не очень-то похож на плоскость.
Вспомните знаменитую картинку с сравнением России и Африки. На картах Россия огромна, а на самом деле площадь Африки аж в два раза больше площади России! Это как раз пример искажения проекции Меркатора.

S2 решает эту проблему использованием исключительно сферической проекции и сферической геометрии. Конечно, Земля — тоже не совсем сфера, но искажениями в случае сферы можно пренебречь для большинства задач.
Работать мы будем с единичной, или unit- сферой, то есть со сферой радиусом 1 и будем использовать такие понятия, как центральный угол, сферический прямоугольник и сферический сегмент.
Название S2 как раз происходит из математической нотации, обозначающей unit-сферу.
Но пугаться не стоит, так как практически всю математику берёт на себя библиотека.
Второй (и самой важной) особенностью библиотеки является понятие иерархического разбиения земного шара на клетки (по-английски — cells).
Разбиение иерархично, то есть присутствует такое понятие, как уровень (или level) клетки. И на одном уровне клетки имеют примерно одинаковый размер.
Клетками можно задать любую точку на Земле. Если воспользоваться клеткой максимального, 30-го, уровня, которая имеет размер меньше сантиметра по ширине, то точность, как вы понимаете, будет очень высокой. Клетками более низкого уровня можно задать ту же самую точку, но точность уже будет меньше. Например, 5 м на 5 м.
Клетками можно задавать не только точки, но и более сложные объекты типа полигонов и каких-то областей (на картинке вы, например, видите Гавайи). В этом случае такие фигуры будут заданы наборами клеток (возможно, разных уровней).
Такое разбиение очень компактно: каждая клетка может быть закодирована одним 64-битным числом.
Я упомянул о том, что клетка задаётся одним 64-битным числом. Вот оно! Получается, что координата или точка на Земле, которая по умолчанию задаётся двумя координатами, с которыми нам неудобно работать стандартными методами, может быть задана одним числом. Но как этого добиться? Давайте посмотрим…
Как происходит то самое иерархическое разбиение сферы?
Мы сначала окружаем сферу кубом и проецируем её на все шесть его граней, чуть-чуть подправив проекцию на ходу, чтобы убрать искажения. Это level 0. Затем мы каждую из шести граней куба можем разбить на четыре равные части — это level 1. И каждую из получившихся четырёх частей можно разбить ещё на четыре равные части — level 2. И так далее до level 30.

Но на данном этапе у нас всё ещё присутствует двумерность. И здесь на подмогу нам приходит математическая идея из далёкого прошлого. В конце XIX века Дейвид Гильберт придумал способ заполнения любого пространства одномерной линией, которая поворачивает, сворачивается и таким образом заполняет пространство. Гильбертовая кривая рекурсивна, а это значит, что точность или плотность заполнения можно выбирать. Любой мелкий кусок мы можем при необходимости заполнить плотнее.
Мы можем заполнить такой кривой наше двумерное пространство. И если теперь взять эту кривую и растянуть её в прямую (как будто мы вытягиваем ниточку), то мы получим одномерный объект, описывающий многомерный объект, — одномерный объект или координату на этой линии, с которой удобно и просто работать.
Примерно так выглядит заполнение Гильбертовой кривой Земли на одном из срединных уровней:

Ещё одной особенностью Гильбертовой кривой является тот факт, что точки, находящиеся рядом на кривой, находятся рядом и в пространстве. Обратное не всегда, но в основном тоже верно. И вот эту особенность мы тоже будем активно применять.
Но почему мы можем любую клетку закодировать одним 64-битным числом, которое, кстати, называется CellID? Давайте посмотрим.
У нас шесть граней куба. Шесть разных значений можно закодировать тремя битами. Вспоминаем логарифмы.
Затем мы каждую из шести граней разбиваем на четыре равные части 30 раз. Чтобы задать одну из четырёх частей, на которые мы разбиваем клетку на каждом из уровней, нам хватит двух бит.
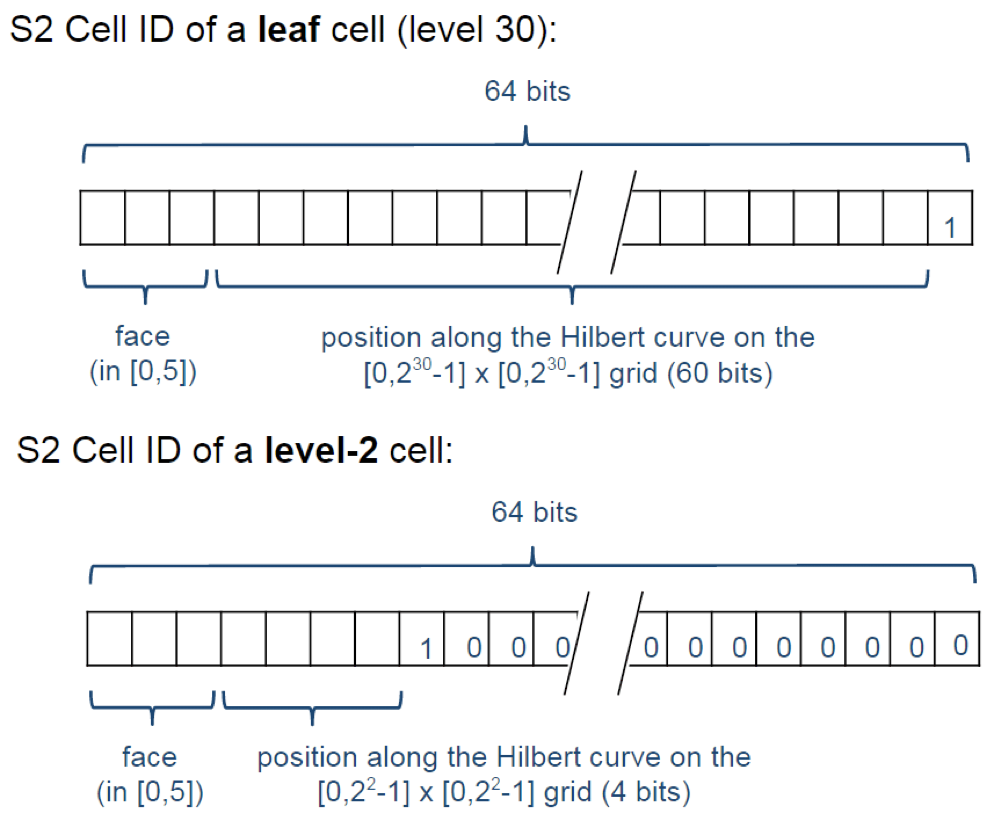
Итого 3 + 2*30 = 63. А один лишний бит мы выставим в конце, чтобы знать и быстро понимать, какого уровня клетка задаётся данным CellID.

Что нам дают все эти разбиения и кодирование Гильбертовой кривой в одно число?
Теперь, чтобы закрепить эти теоретические знания, давайте рассмотрим два примера. Мы напишем два простых сервиса, и первый из них — просто поиск «вокруг».
Мы сделаем поисковый индекс. Нам понадобится функция для создания индекса, функция для добавления человека в индекс и, собственно, функция поиска. Ну и тест.
Пользователь задаётся своим ID и координатами, а поиск — координатами центра поиска и радиусом поиска.
В индексе нам понадобится B-tree, в узлах которого мы будем хранить ячейку уровня storageLevel и список пользователей в данной ячейке. Уровень ячейки storageLevel — это выбор между точностью первоначального поиска и производительностью. В этом примере мы воспользуемся ячейкой размера примерно 1 км на 1 км. Функция Less необходима для работы B-tree, для того, чтобы дерево могло понять, какое из наших значений меньше, а какое — больше.
Теперь давайте посмотрим на функцию добавления пользователя.

Здесь мы впервые видим S2 в деле. Мы преобразовываем наши координаты, заданные в градусах, в радианы, а затем — в CellID, который соответствует этим координатам на максимальном 30-м уровне (то есть с минимальным размером клетки), и преобразуем полученный CellID в CellID того уровня, на котором мы будем хранить людей. Если заглянуть «внутрь» этой функции, мы увидим просто обнуление нескольких бит. Вспомните, как у нас кодируется CellID.
Затем нам всего лишь нужно добавить данного пользователя в соответствующую клетку в B-tree. Или первым, или в конец списка, если там кто-то уже есть. Наш простой индекс готов.
Переходим к функции поиска. Первые преобразования похожи, но вместо клетки мы по координатам получаем объект «точка». Это центр нашего поиска.
Далее по радиусу, заданному в метрах, мы получаем центральный угол. Это угол, исходящий из центра сферы. Преобразование в данном случае простое: достаточно разделить наш радиус в метрах на радиус Земли в метрах.
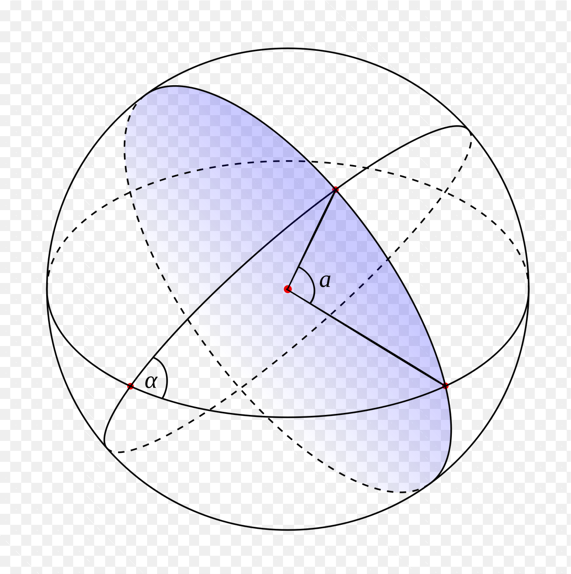
По точке центра поиска и по углу, которые мы только что получили, мы можем вычислить сферический сегмент (или «шапочку»). По сути, это окружность на сфере, но только трёхмерная.
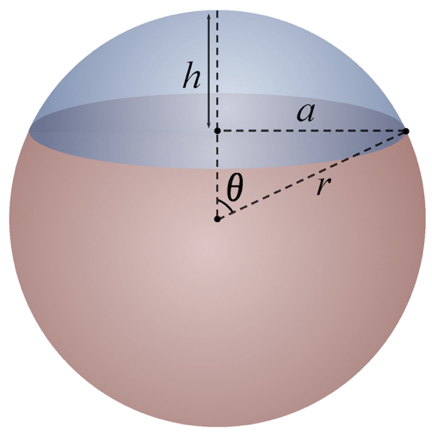
Отлично, у нас есть «шапочка», внутри которой нам нужно искать. Но как? Для этого мы попросим S2 дать нам список клеток уровня storageLevel, которые полностью покрывают наш круг или нашу «шапочку».
Выглядит это примерно так:
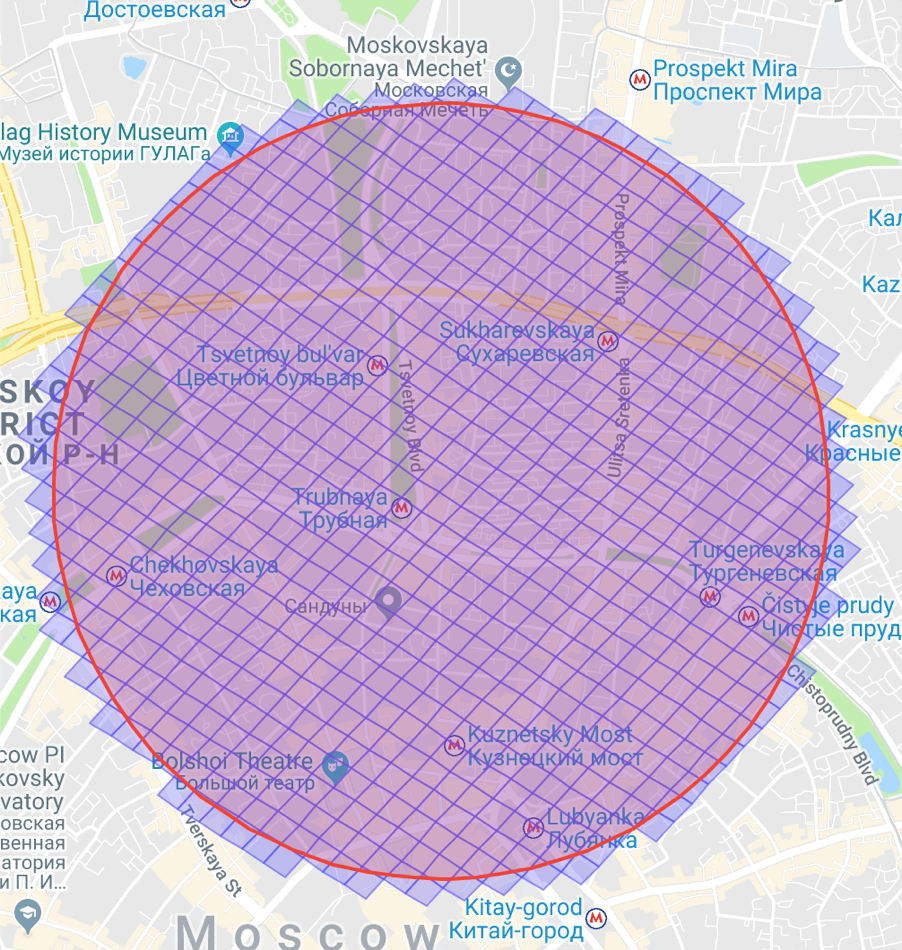
Осталось лишь пройтись по полученным клеткам и get-ами в B-tree получить всех пользователей, что находятся внутри.
Для теста мы создадим индекс и несколько пользователей. Трёх поближе, двух — подальше. И проверим, чтобы в случае маленького радиуса возвращались только три пользователя, а в случае большего радиуса — все. Ура! Наша простенькая программка работает.
Но в ней есть один довольно очевидный недостаток. В случае большого радиуса поиска и маленькой плотности заполнения людьми, нужно будет get-ами проверять очень и очень много клеток. Это не так быстро.
Вспомните, что мы просили S2 покрыть нашу «шапочку» именно клетками уровня storageLevel. Но поскольку эти клетки довольно маленькие, то их получается много.
Мы можем попросить S2 покрыть «шапочку» клетками разного уровня; тогда получится что-то вроде этого:
Как видите, S2 использует внутри круга клетки большего размера, а по краям — меньшего. В сумме же клеток становится меньше.
Но для того чтобы в нашем B-дереве найти пользователей из бОльших клеток, мы уже не можем пользоваться Get. Нам нужно спросить у S2 для каждой большой клетки номер первой внутренней клетки нашего уровня storageLevel и номер последней и искать уже с помощью range scan, то есть запросом «от» и «до».
Изменение совсем незначительное, но давайте посмотрим на него в процессе работы. Напишем простенькие бенчмарки, которые в цикле занимаются поиском, и запустим их.
Наше маленькое изменение привело к ускорению на три порядка. Неплохо!
Мы с вами рассмотрели суперпростую реализацию поиска по радиусу. Давайте теперь быстренько пройдёмся по такой же простой реализации geofencing-а, то есть определения, в каком полигоне мы находимся или какой полигон ближайший к нам.
Здесь в нашем индексе нам аналогично понадобится B-tree, но в дополнение к нему у нас будет глобальный map всех добавленных полигонов.
В узлах B-дерева, как и раньше, мы будем хранить список, но только теперь уже полигонов, которые находятся в ячейке уровня storageLevel.
В данном примере у нас будут функции добавления полигона в индекс, поиска полигона, в котором мы находимся, и поиска ближайшего полигона.
Начнём с добавления полигона. Полигон задаётся списком вершин, причём S2 ожидает, что порядок вершин будет против часовой стрелки. Но в случае ошибки у нас будет функция «нормализации», которая как бы выворачивает его наизнанку.
Список точек-вершин мы преобразуем в Loop, а затем и в полигон. Разница между ними в том, что полигон может состоять из нескольких loop-ов, иметь дырку, например, как пончик.
Как и в прошлом примере, мы попросим S2 покрыть наш полигон клетками и каждую из возвращённых клеток добавим в B-tree. Ну и в глобальный map.
Функция поиска полигона, в котором мы находимся, в данном примере тривиальна. Как и раньше, преобразуем координату поиска в CellID на уровне storageLevel и находим или не находим эту клетку в B-дереве.
Поиск ближайшего полигона чуть сложнее. Сначала мы попробуем определить, вдруг мы уже находимся в каком-то полигоне. Если нет, то мы будем искать по увеличивающемуся радиусу (ниже я покажу, как это выглядит). Ну и когда мы найдём ближайшие полигоны, мы отфильтруем их и найдём самый ближайший, вычислив расстояние до каждого из найденных и взяв тот, расстояние до которого наименьшее.
Что значит «по увеличивающемуся радиусу»? На первой картинке вы видите оранжевую клетку — центр нашего поиска. Сначала мы попробуем найти ближайший полигон во всех соседних клетках (на картинке они серые). Если мы ничего там не найдём, то отдалимся ещё на один уровень, как на второй картинке. И так далее.


«Соседей» нам даёт функция AllNeighbors. Разве что нужно полученные клетки отфильтровать и убрать те, которые мы уже просмотрели.
Вот, собственно, и всё. Для этого примера я также написал тест, и он успешно проходит.
Если вам интересно взглянуть на него или на полные примеры, то их можно найти здесь вместе со слайдами.
Если вам когда-нибудь понадобится написать поисковый сервис, работающий с координатами или какими-то более сложными географическими объектами, и вы не захотите или не сможете использовать готовые СУБД типа PostGIS, вспомните об S2.
Это классный и простой инструмент, который даст вам базовые вещи и фреймворк для работы с координатами и земным шаром. Мы в Badoo очень любим S2 и всячески её рекомендуем.
Спасибо!
Upd: А вот и видео подоспело!
Меня зовут Марко, я работаю в Badoo в команде «Платформа». Не так давно на GopherCon Russia 2018 я рассказывал, как работать с координатами. Для тех, кто не любит смотреть видео (и всех интересующихся, конечно), публикую текстовый вариант своего доклада.

Введение
Сейчас у большинства людей в мире есть смартфон с постоянным доступом в Интернет. Если говорить в цифрах, то в 2018 году смартфон будет у почти 5 млрд людей, и 60% из них пользуются мобильным Интернетом.
Это огромные числа. Компаниям получать координаты пользователей стало легко и просто. Эти лёгкость и доступность породили (и продолжают порождать) огромное количество сервисов, основанных на координатах.
Всем нам известны компании типа Uber, игры, покорившие мир, такие как Ingress и Pokemon Go. Да что уж там, в любом банковском приложении есть возможность увидеть банкоматы или скидки поблизости.
Мы в Badoo также очень активно используем координаты, чтобы предоставлять своим пользователям лучший, актуальный и интересный для них сервис. Но о каком именно использовании идёт речь? Давайте посмотрим на примеры сервисов, которые у нас есть.
Geo-сервисы в Badoo
Первый пример: Meetmaker и Geousers
Badoo — это в первую очередь дейтинг. Место, где люди знакомятся друг с другом. Одним из важных критериев при поиске людей является расстояние. Ведь в большинстве случаев девушке из Москвы хочется познакомиться с мальчиком, который находится в паре километров от неё или по крайней мере тоже живёт в Москве, а не в далёком Владивостоке.

Сервисы, которые подбирают вам людей для «игры» «Да/нет» или показывают пользователей вокруг, занимаются поиском людей с подходящими вам критериями в каком-то радиусе от вас.
Второй пример: Geoborder
Для того чтобы ответить на вопросы, в каком городе находится пользователь, в какой стране или, ещё более точно, к примеру, в каком аэропорту или в каком университете, мы используем сервис Geoborder, который занимается так называемым geofencing-ом.

Самым простым способом ответить на эти вопросы было бы считать расстояние от пользователя до центра города или центра университета, но этот подход очень неточен и зависит от большого количества граничных условий.
Поэтому у нас расчерчены очень точные границы стран, городов, важных объектов (например, университетов и аэропортов, о которых я говорил). Эти границы задаются полигонами. Имея набор таких границ, мы можем понять, находится ли пользователь внутри полигона, или найти ближайший к нему полигон. Соответственно, мы можем сказать, в каком он городе, или найти ближайший к нему город.
Третий пример: Bumpd

У нас есть очень популярная фича под названием Bumped Into, которая в фоновом режиме постоянно ищет пересечения пользователей во времени и в пространстве и показывает вам, что вот с этим мальчиком или с этой девушкой вы регулярно бываете в одном месте в одно и то же время или регулярно ходите одной дорогой. Эта фича очень нравится пользователям, поскольку является ещё одним поводом познакомиться и темой, с которой можно начать разговор.
Четвёртый пример: Geocache — кеширование гео-информации, которую дорого «доставать»
Ну и последний пример, о котором я упомяну, связан с кешированием гео-информации. Представьте себе, что вы используете данные из, например, Booking.com, который предоставляет вам информацию о гостиницах вокруг, но лезть в Booking.com каждый раз — слишком долго. Ваша труба в Интернет, возможно, довольно узкая, как яма у этого гофера. Возможно, сервис, в который вы идёте за данными, берёт деньги за каждый запрос, и вам хочется немного сэкономить.

В этом случае неплохо бы иметь кеширующий слой, который заметно уменьшит количество запросов в медленный или дорогой сервис, а наружу будет предоставлять очень похожий API. Сервис, который будет понимать, что обо всех или о большинстве гостиниц в данной области он уже знает, эти данные относительно свежи, и, соответственно, можно не лезть за ними во внешний сервис. Такого рода задачи у нас решаются сервисом под названием Geocache.
Особенности geo-сервисов
Мы с вами уже поняли, что координат много, координаты — это важно, и на основе них можно сделать очень много интересных сервисов. Ну и что дальше? В чём, собственно, дело? Чем координаты отличаются от любой другой информации, полученной от пользователя?
А особенностей, я бы сказал, две.

Во-первых, гео-данные трёхмерны, а точнее двумерны, так как в общем случае нас не интересует высота. Они состоят из широты и долготы, и поиск чаще всего идёт одновременно по обеим. Представьте себе поиск в какой-либо области. Стандартные индексы в распространённых СУБД неоптимальны для такого использования.

Во-вторых, многие задачи требуют более сложных типов данных типа полигонов, о которых мы говорили выше на примере сервиса Geoborder в Badoo. Полигоны, конечно, состоят из координат вершин, но требуют дополнительной обработки, и поисковые запросы на таких типах данных тоже сложнее. Мы уже видели запросы «Найти ближайший полигон к точке» или «Найти полигон, который включает данную точку».
Зачем писать свой сервис
Для того чтобы соответствовать этим особенностям, многие СУБД включают в поставку специальные индексы, заточенные под многомерные данные, и дополнительные функции, которые позволяют работать с такими объектами, как полигоны или ломаные.

Наверное, самым ярким примером является PostGIS — расширение к популярной СУБД PostgreSQL, обладающее широчайшими возможностями для работы с координатами и географией.
Но использовать готовую СУБД — не единственное и не всегда лучшее решение.

Если вы не хотите делить бизнес-логику вашего сервиса между ним и СУБД, если вы хотите чего-то, что недоступно в СУБД, если вы хотите полноценно управлять вашим сервисом и не быть ограниченным возможностями масштабирования какой-либо СУБД, например, то вы можете захотеть встроить возможности поиска и работы с geo-данными в свой сервис.
Такой подход, бесспорно, гибче, но может быть и значительно сложнее, потому что СУБД — это решение формата «всё в одном», и многие инфраструктурные вещи типа репликации уже сделаны за вас. Репликации и, собственно, алгоритмов и индексов для работы с координатами.
Но не всё так страшно. Я хотел бы познакомить вас с библиотекой, которая реализует большую часть из того, что вам понадобится. Которая является своеобразным кубиком, легко встраиваемым везде, где вам нужно работать с геометрией на сфере или искать по координатам. С библиотекой под названием S2.
S2

S2 — библиотека для работы с геометрией (в том числе на сфере), предоставляющая очень удобные возможности для создания geo-индексов.
До недавнего времени S2 была практически неизвестна и обладала совсем скудной документацией, но не так давно Google решила "перевыпустить" её в open-source, дополнив выкладку обещанием поддерживать и развивать продукт.
Главная версия библиотеки написана на C++ и имеет несколько официальных портов или версий на других языках, включая Go-версию. Go-версия на сегодняшний день не на 100% реализует всё то, что есть в C++-версии, но того, что есть, достаточно для реализации большинства вещей.
Помимо Google, библиотеку активно используют в таких компаниях, как Foursquare, Uber, Yelp, ну и Badoo, конечно. А среди продуктов, использующих библиотеку внутри, можно выделить всем вам известную MongoDB.
Но пока я не сказал ничего дельного о том, почему именно S2 удобна и почему позволяет легко писать сервисы c geo-поиском. Давайте я исправлюсь и немного погружусь во внутренности, прежде чем мы рассмотрим два примера.
Проекция

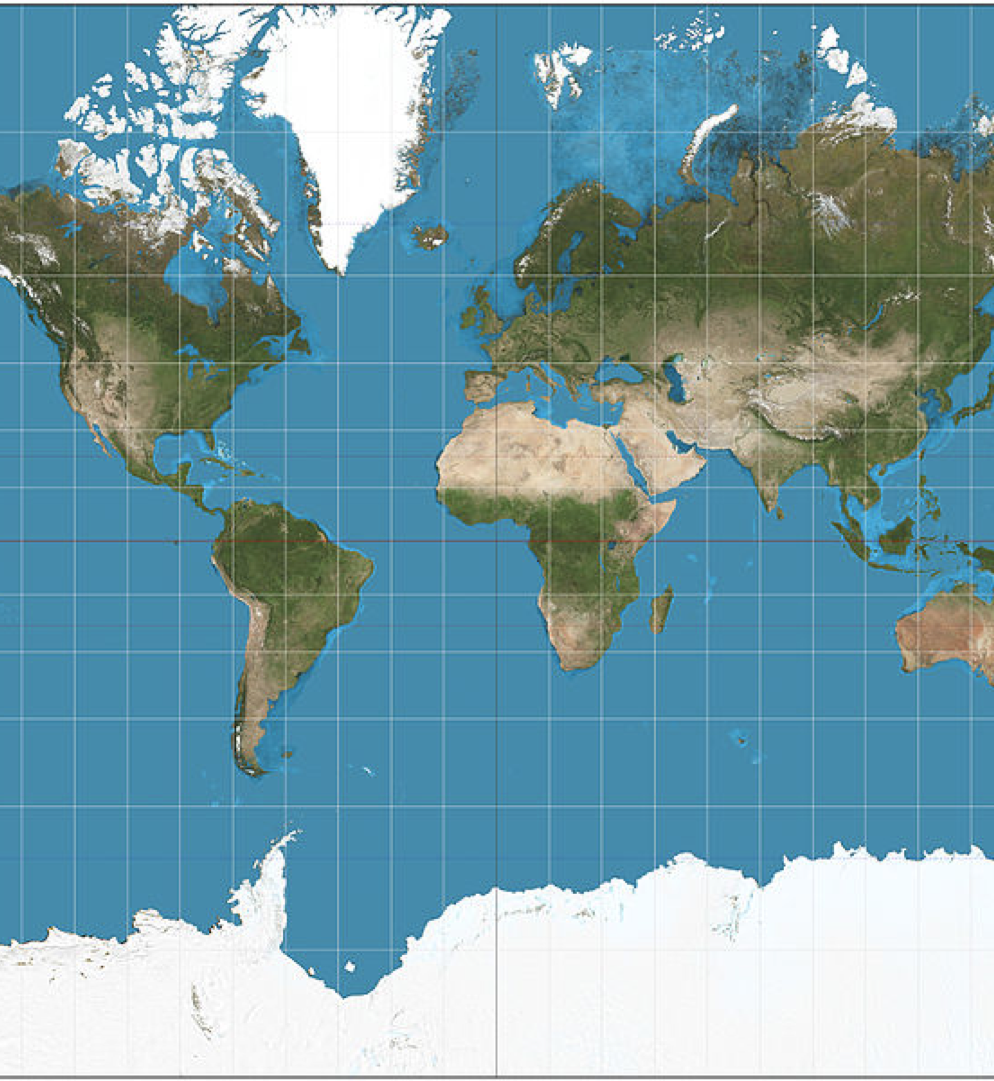
Обычно география подразумевает использование одной из распространённых проекций земного шара на плоскость. Например, всем нам известной проекции Меркатора. Недостаток такого подхода заключается в том, что любая проекция так или иначе имеет искажения. Наш с вами земной шар не очень-то похож на плоскость.

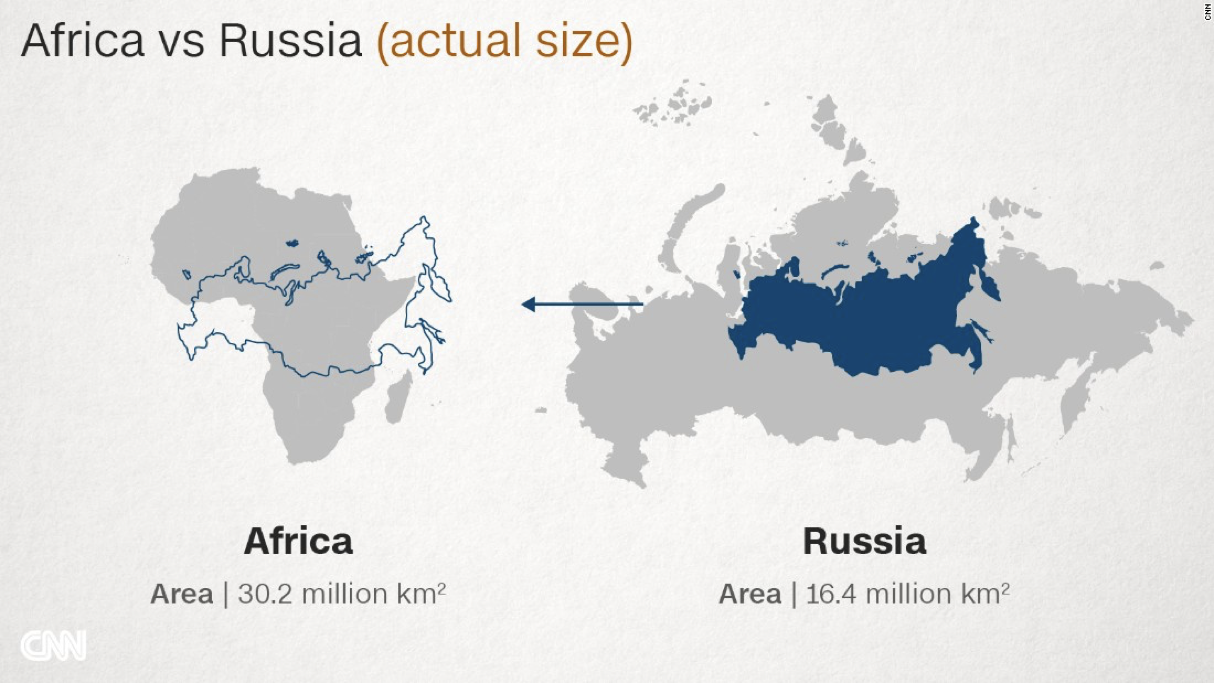
Вспомните знаменитую картинку с сравнением России и Африки. На картах Россия огромна, а на самом деле площадь Африки аж в два раза больше площади России! Это как раз пример искажения проекции Меркатора.

S2 решает эту проблему использованием исключительно сферической проекции и сферической геометрии. Конечно, Земля — тоже не совсем сфера, но искажениями в случае сферы можно пренебречь для большинства задач.
Работать мы будем с единичной, или unit- сферой, то есть со сферой радиусом 1 и будем использовать такие понятия, как центральный угол, сферический прямоугольник и сферический сегмент.
Название S2 как раз происходит из математической нотации, обозначающей unit-сферу.
Но пугаться не стоит, так как практически всю математику берёт на себя библиотека.
Иерархические клетки (cells)
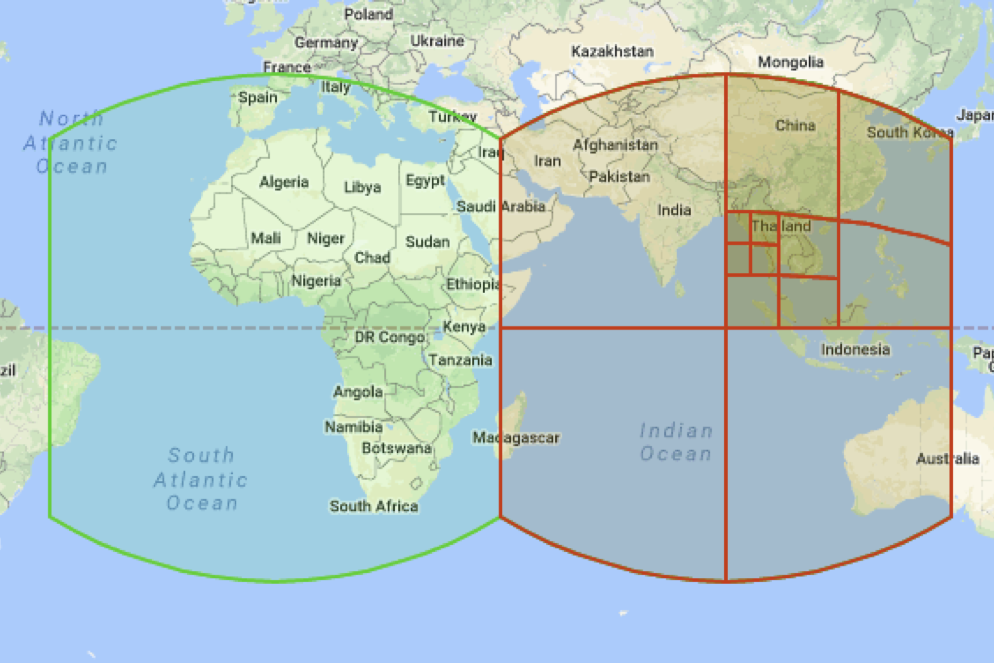
Второй (и самой важной) особенностью библиотеки является понятие иерархического разбиения земного шара на клетки (по-английски — cells).

Разбиение иерархично, то есть присутствует такое понятие, как уровень (или level) клетки. И на одном уровне клетки имеют примерно одинаковый размер.
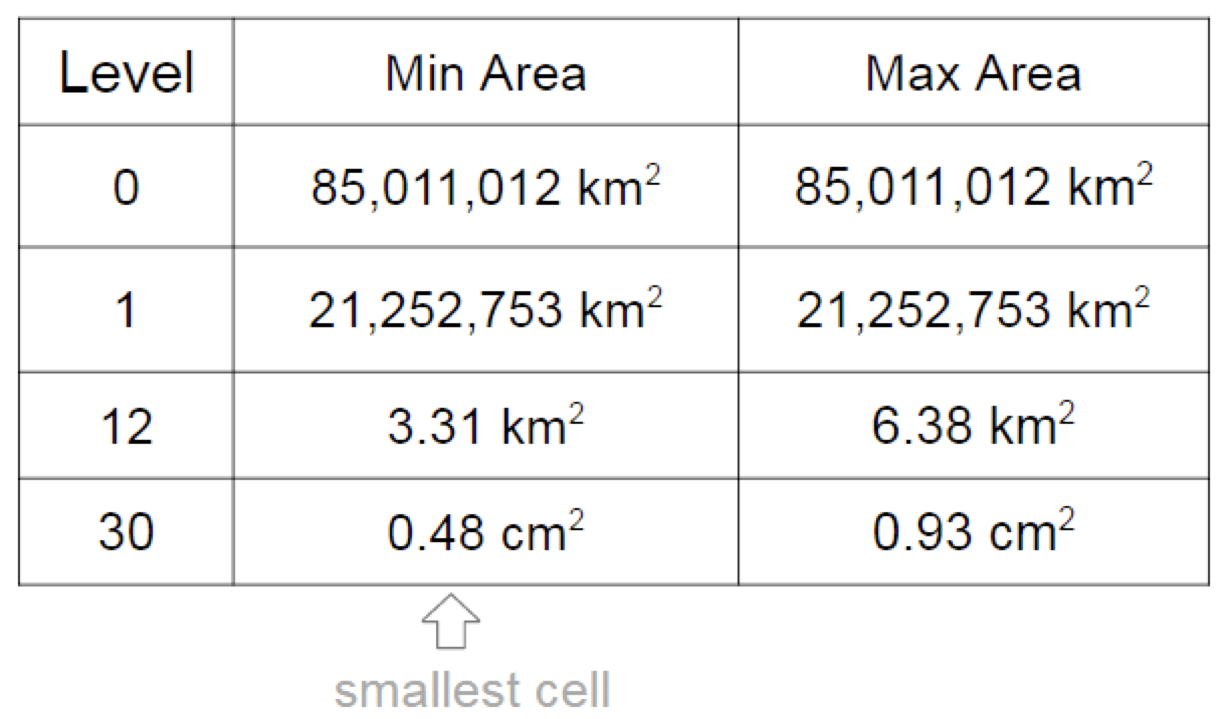
Клетками можно задать любую точку на Земле. Если воспользоваться клеткой максимального, 30-го, уровня, которая имеет размер меньше сантиметра по ширине, то точность, как вы понимаете, будет очень высокой. Клетками более низкого уровня можно задать ту же самую точку, но точность уже будет меньше. Например, 5 м на 5 м.

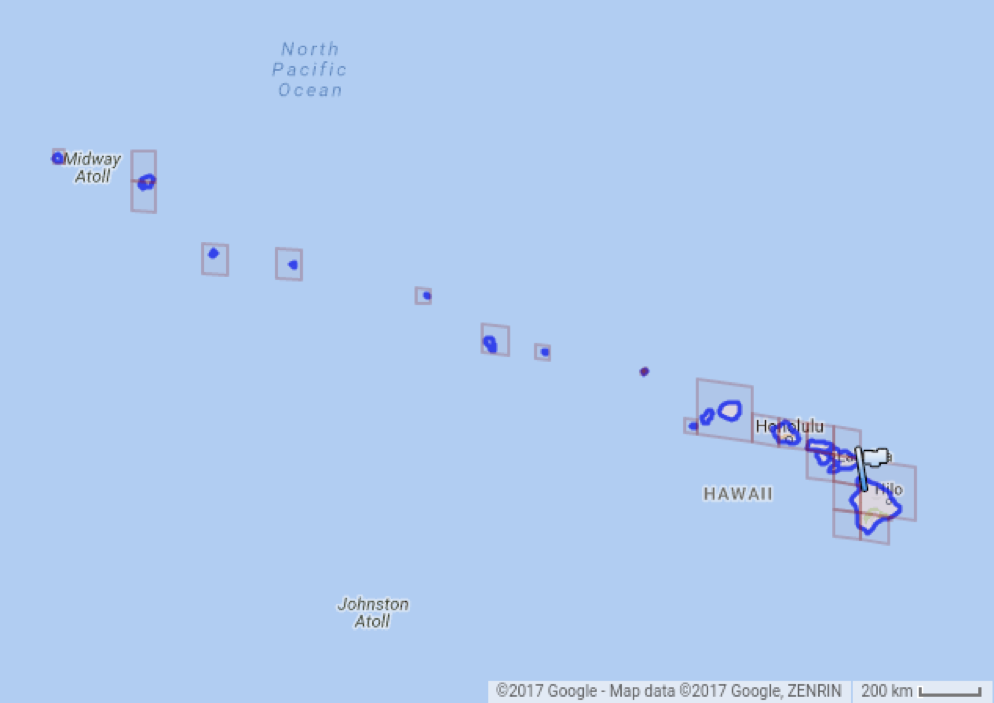
Клетками можно задавать не только точки, но и более сложные объекты типа полигонов и каких-то областей (на картинке вы, например, видите Гавайи). В этом случае такие фигуры будут заданы наборами клеток (возможно, разных уровней).

Такое разбиение очень компактно: каждая клетка может быть закодирована одним 64-битным числом.
Кривая Гильберта
Я упомянул о том, что клетка задаётся одним 64-битным числом. Вот оно! Получается, что координата или точка на Земле, которая по умолчанию задаётся двумя координатами, с которыми нам неудобно работать стандартными методами, может быть задана одним числом. Но как этого добиться? Давайте посмотрим…
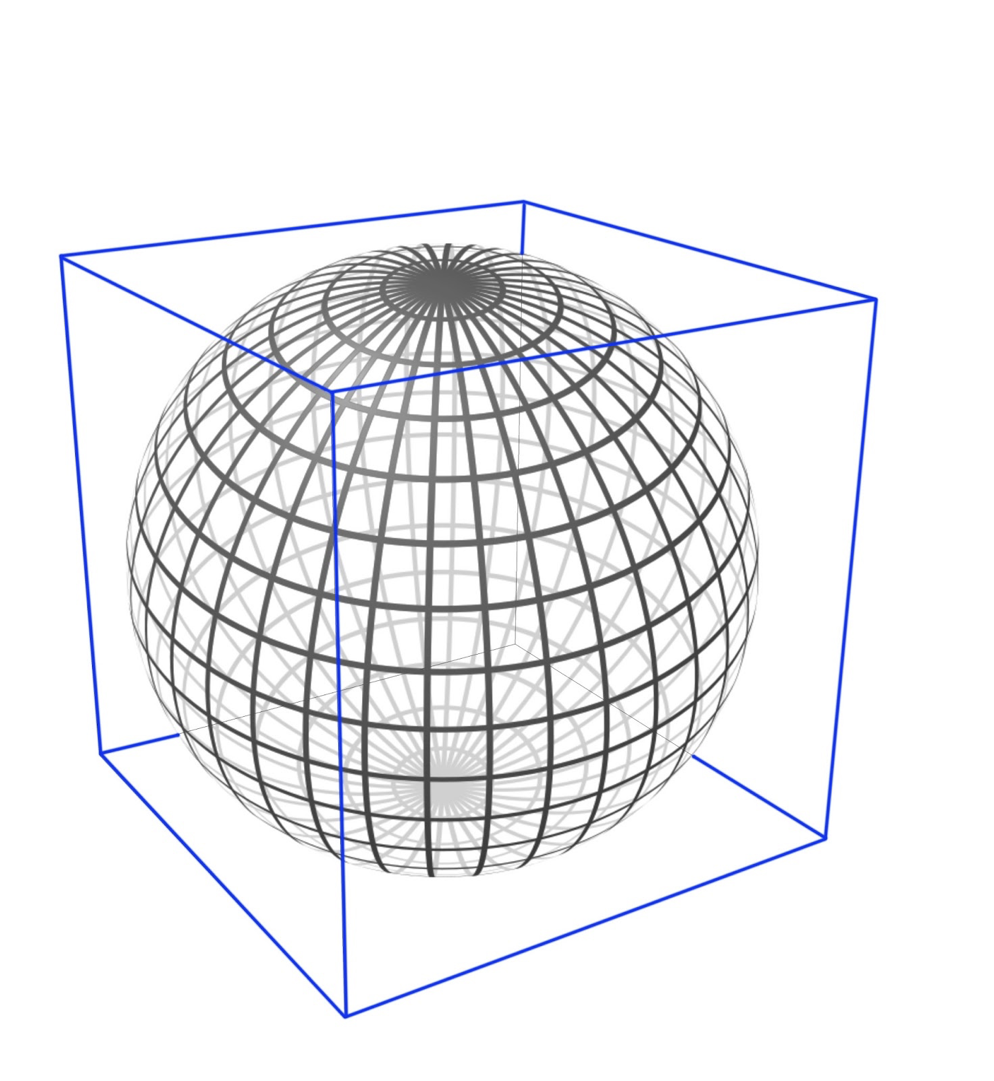
Как происходит то самое иерархическое разбиение сферы?

Мы сначала окружаем сферу кубом и проецируем её на все шесть его граней, чуть-чуть подправив проекцию на ходу, чтобы убрать искажения. Это level 0. Затем мы каждую из шести граней куба можем разбить на четыре равные части — это level 1. И каждую из получившихся четырёх частей можно разбить ещё на четыре равные части — level 2. И так далее до level 30.

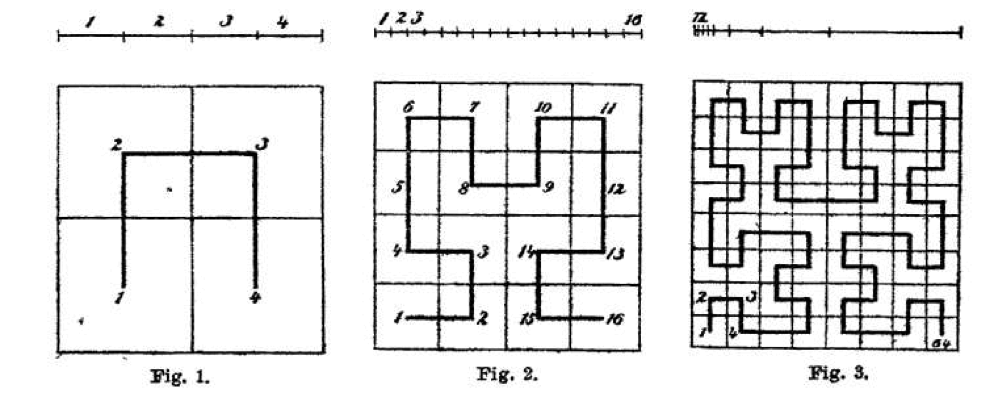
Но на данном этапе у нас всё ещё присутствует двумерность. И здесь на подмогу нам приходит математическая идея из далёкого прошлого. В конце XIX века Дейвид Гильберт придумал способ заполнения любого пространства одномерной линией, которая поворачивает, сворачивается и таким образом заполняет пространство. Гильбертовая кривая рекурсивна, а это значит, что точность или плотность заполнения можно выбирать. Любой мелкий кусок мы можем при необходимости заполнить плотнее.

Мы можем заполнить такой кривой наше двумерное пространство. И если теперь взять эту кривую и растянуть её в прямую (как будто мы вытягиваем ниточку), то мы получим одномерный объект, описывающий многомерный объект, — одномерный объект или координату на этой линии, с которой удобно и просто работать.
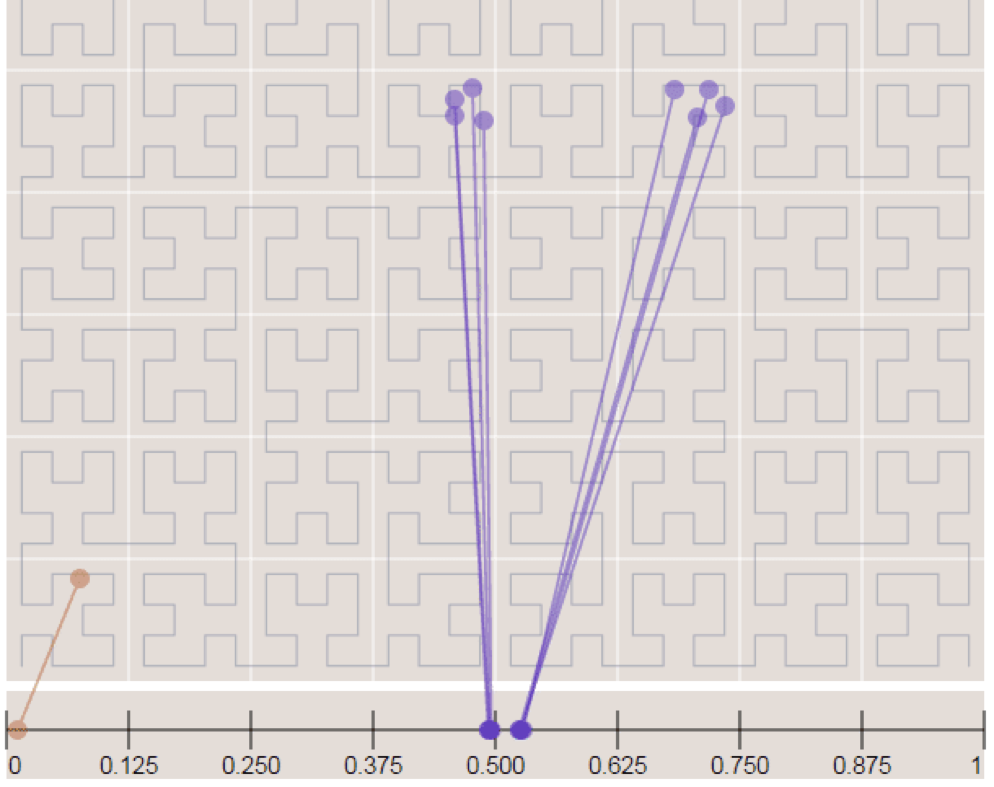
Примерно так выглядит заполнение Гильбертовой кривой Земли на одном из срединных уровней:

Ещё одной особенностью Гильбертовой кривой является тот факт, что точки, находящиеся рядом на кривой, находятся рядом и в пространстве. Обратное не всегда, но в основном тоже верно. И вот эту особенность мы тоже будем активно применять.

Кодирование в 64-битную переменную
Но почему мы можем любую клетку закодировать одним 64-битным числом, которое, кстати, называется CellID? Давайте посмотрим.
У нас шесть граней куба. Шесть разных значений можно закодировать тремя битами. Вспоминаем логарифмы.
Затем мы каждую из шести граней разбиваем на четыре равные части 30 раз. Чтобы задать одну из четырёх частей, на которые мы разбиваем клетку на каждом из уровней, нам хватит двух бит.

Итого 3 + 2*30 = 63. А один лишний бит мы выставим в конце, чтобы знать и быстро понимать, какого уровня клетка задаётся данным CellID.

Что нам дают все эти разбиения и кодирование Гильбертовой кривой в одно число?
- Мы можем любую точку на земном шаре закодировать одним CellID. В зависимости от уровня мы получаем разную точность.
- Любой двумерный объект на земном шаре мы можем закодировать одним или несколькими CellID. Аналогично мы можем играть с точностью, варьируя уровни.
- Свойство Гильбертовой кривой, заключающееся в том, что точки, которые находятся рядом на ней, находятся рядом и в пространстве, и тот факт что CellID у нас — просто число, позволяют нам для поиска пользоваться обычным деревом типа B-дерева. В зависимости от того, что мы ищем (точку или область), мы будем пользоваться или get, или range scan, то есть поиском «от» и «до».
- Разбиение земного шара на уровни даёт нам простой фреймворк для шардинга нашей системы. К примеру, на нулевом уровне мы можем разделить наш сервис на шесть инстансов, на первом уровне — на 24 и т. д.
Теперь, чтобы закрепить эти теоретические знания, давайте рассмотрим два примера. Мы напишем два простых сервиса, и первый из них — просто поиск «вокруг».
Примеры
Напишем сервис поиска людей вокруг
Мы сделаем поисковый индекс. Нам понадобится функция для создания индекса, функция для добавления человека в индекс и, собственно, функция поиска. Ну и тест.
type Index struct {}
func NewIndex(storageLevel int) *Index {}
func (i *Index) AddUser(userID uint32, lon, lat float64) error {}
func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {}
func TestSearch(t *testing.T) {}
Пользователь задаётся своим ID и координатами, а поиск — координатами центра поиска и радиусом поиска.
В индексе нам понадобится B-tree, в узлах которого мы будем хранить ячейку уровня storageLevel и список пользователей в данной ячейке. Уровень ячейки storageLevel — это выбор между точностью первоначального поиска и производительностью. В этом примере мы воспользуемся ячейкой размера примерно 1 км на 1 км. Функция Less необходима для работы B-tree, для того, чтобы дерево могло понять, какое из наших значений меньше, а какое — больше.
type Index struct {
storageLevel int
bt *btree.BTree
}
type userList struct {
cellID s2.CellID
list []uint32
}
func (ul userList) Less(than btree.Item) bool {
return uint64(ul.cellID) < uint64(than.(userList).cellID)
}
Теперь давайте посмотрим на функцию добавления пользователя.
func (i *Index) AddUser(userID uint32, lon, lat float64) error {
latlng := s2.LatLngFromDegrees(lat, lon)
cellID := s2.CellIDFromLatLng(latlng)
cellIDOnStorageLevel := cellID.Parent(i.storageLevel)
// ...
}

Здесь мы впервые видим S2 в деле. Мы преобразовываем наши координаты, заданные в градусах, в радианы, а затем — в CellID, который соответствует этим координатам на максимальном 30-м уровне (то есть с минимальным размером клетки), и преобразуем полученный CellID в CellID того уровня, на котором мы будем хранить людей. Если заглянуть «внутрь» этой функции, мы увидим просто обнуление нескольких бит. Вспомните, как у нас кодируется CellID.
func (i *Index) AddUser(userID uint32, lon, lat float64) error {
// ...
ul := userList{cellID: cellIDOnStorageLevel, list: nil}
item := i.bt.Get(ul)
if item != nil {
ul = item.(userList)
}
ul.list = append(ul.list, userID)
i.bt.ReplaceOrInsert(ul)
return nil
}
Затем нам всего лишь нужно добавить данного пользователя в соответствующую клетку в B-tree. Или первым, или в конец списка, если там кто-то уже есть. Наш простой индекс готов.
Переходим к функции поиска. Первые преобразования похожи, но вместо клетки мы по координатам получаем объект «точка». Это центр нашего поиска.
func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {
latlng := s2.LatLngFromDegrees(lat, lon)
centerPoint := s2.PointFromLatLng(latlng)
centerAngle := float64(radius) / EarthRadiusM
cap := s2.CapFromCenterAngle(centerPoint, s1.Angle(centerAngle))
// ...
return result, nil
}
Далее по радиусу, заданному в метрах, мы получаем центральный угол. Это угол, исходящий из центра сферы. Преобразование в данном случае простое: достаточно разделить наш радиус в метрах на радиус Земли в метрах.

По точке центра поиска и по углу, которые мы только что получили, мы можем вычислить сферический сегмент (или «шапочку»). По сути, это окружность на сфере, но только трёхмерная.

Отлично, у нас есть «шапочка», внутри которой нам нужно искать. Но как? Для этого мы попросим S2 дать нам список клеток уровня storageLevel, которые полностью покрывают наш круг или нашу «шапочку».
func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {
// ...
rc := s2.RegionCoverer{MaxLevel: i.storageLevel, MinLevel: i.storageLevel}
cu := rc.Covering(cap)
// ...
return result, nil
}
Выглядит это примерно так:

Осталось лишь пройтись по полученным клеткам и get-ами в B-tree получить всех пользователей, что находятся внутри.
func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {
// ...
var result []uint32
for _, cellID := range cu {
item := i.bt.Get(userList{cellID: cellID})
if item != nil {
result = append(result, item.(userList).list...)
}
}
return result, nil
}
Для теста мы создадим индекс и несколько пользователей. Трёх поближе, двух — подальше. И проверим, чтобы в случае маленького радиуса возвращались только три пользователя, а в случае большего радиуса — все. Ура! Наша простенькая программка работает.
func prepare() *Index {
i := NewIndex(13 /* ~ 1km */)
i.AddUser(1, 14.1313, 14.1313)
i.AddUser(2, 14.1314, 14.1314)
i.AddUser(3, 14.1311, 14.1311)
i.AddUser(10, 14.2313, 14.2313)
i.AddUser(11, 14.0313, 14.0313)
return i
}
func TestSearch(t *testing.T) {
indx := prepare()
found, _ := indx.Search(14.1313, 14.1313, 2000)
if len(found) != 3 {
t.Fatal("error while searching with radius 2000")
}
found, _ = indx.Search(14.1313, 14.1313, 20000)
if len(found) != 5 {
t.Fatal("error while searching with radius 20000")
}
}
$ go test -run 'TestSearch$'
PASS
ok github.com/mkevac/gophercon-russia-2018/geosearch 0.008s
Но в ней есть один довольно очевидный недостаток. В случае большого радиуса поиска и маленькой плотности заполнения людьми, нужно будет get-ами проверять очень и очень много клеток. Это не так быстро.
Вспомните, что мы просили S2 покрыть нашу «шапочку» именно клетками уровня storageLevel. Но поскольку эти клетки довольно маленькие, то их получается много.
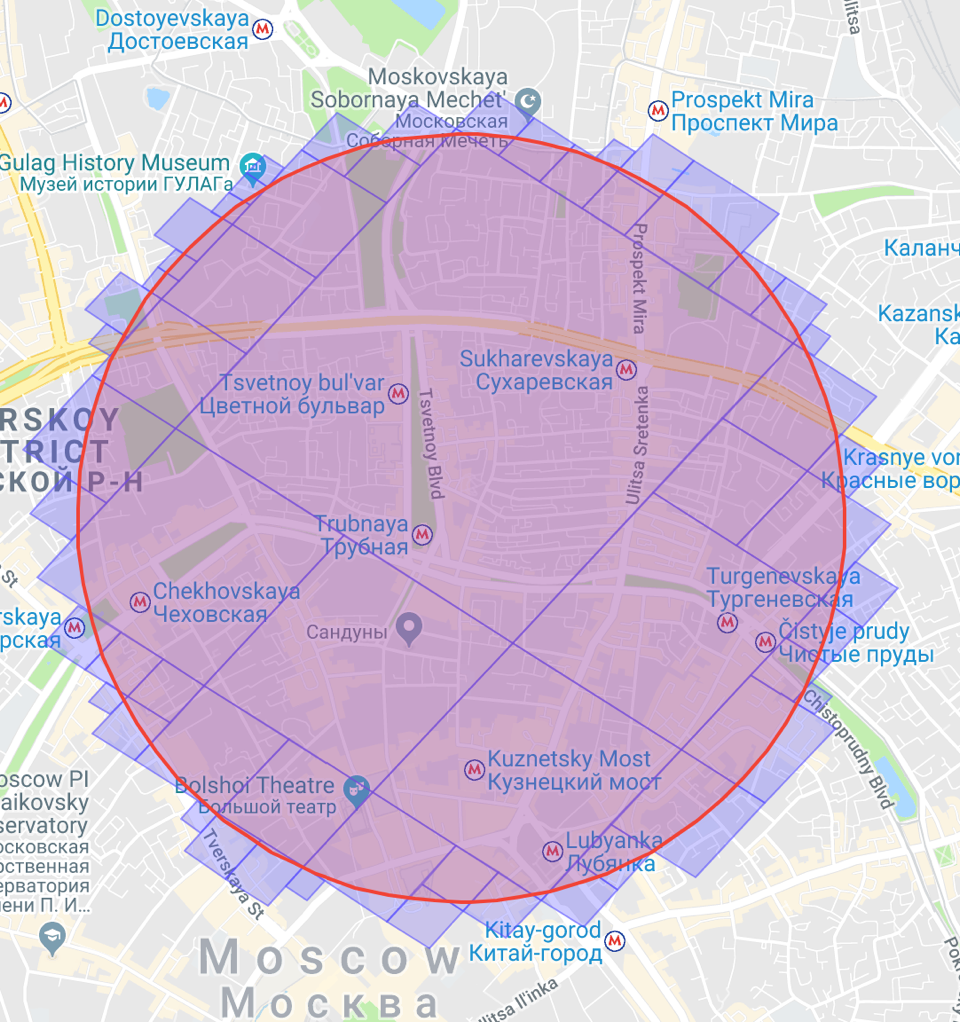
Мы можем попросить S2 покрыть «шапочку» клетками разного уровня; тогда получится что-то вроде этого:
rc := s2.RegionCoverer{MaxLevel: i.storageLevel}
cu := rc.Covering(cap)

Как видите, S2 использует внутри круга клетки большего размера, а по краям — меньшего. В сумме же клеток становится меньше.
Но для того чтобы в нашем B-дереве найти пользователей из бОльших клеток, мы уже не можем пользоваться Get. Нам нужно спросить у S2 для каждой большой клетки номер первой внутренней клетки нашего уровня storageLevel и номер последней и искать уже с помощью range scan, то есть запросом «от» и «до».
func (i *Index) SearchFaster(lon, lat float64, radius uint32) ([]uint32, error) {
// ...
for _, cellID := range cu {
if cellID.Level() < i.storageLevel
begin := cellID.ChildBeginAtLevel(i.storageLevel)
end := cellID.ChildEndAtLevel(i.storageLevel)
i.bt.AscendRange(userList{cellID: begin}, userList{cellID: end.Next()},func(item btree.Item) bool {
result = append(result, item.(userList).list...)
return true
})
} else {
// ...
}
}
return result, nil
}
Изменение совсем незначительное, но давайте посмотрим на него в процессе работы. Напишем простенькие бенчмарки, которые в цикле занимаются поиском, и запустим их.
var res []uint32
func BenchmarkSearch(b *testing.B) {
indx := prepare()
for i := 0; i < b.N; i++ {
res, _ = indx.Search(14.1313, 14.1313, 50000)
}
}
func BenchmarkSearchFaster(b *testing.B) {
indx := prepare()
for i := 0; i < b.N; i++ {
res, _ = indx.SearchFaster(14.1313, 14.1313, 50000)
}
}
Наше маленькое изменение привело к ускорению на три порядка. Неплохо!
$ go test -bench=.
goos: darwin
goarch: amd64
pkg: github.com/mkevac/gophercon-russia-2018/geosearch
BenchmarkSearch-8 500 3097564 ns/op
BenchmarkSearchFaster-8 200000 7198 ns/op
PASS
ok github.com/mkevac/gophercon-russia-2018/geosearch 3.393sДавайте напишем geofencing-сервис
Мы с вами рассмотрели суперпростую реализацию поиска по радиусу. Давайте теперь быстренько пройдёмся по такой же простой реализации geofencing-а, то есть определения, в каком полигоне мы находимся или какой полигон ближайший к нам.
Здесь в нашем индексе нам аналогично понадобится B-tree, но в дополнение к нему у нас будет глобальный map всех добавленных полигонов.
type Index struct {
storageLevel int
bt *btree.BTree
polygons map[uint32]*s2.Polygon
}
func NewIndex(storageLevel int) *Index {
return &Index{
storageLevel: storageLevel,
bt: btree.New(35),
polygons: make(map[uint32]*s2.Polygon),
}
}
В узлах B-дерева, как и раньше, мы будем хранить список, но только теперь уже полигонов, которые находятся в ячейке уровня storageLevel.
type IndexItem struct {
cellID s2.CellID
polygonsInCell []uint32
}
func (ii IndexItem) Less(than btree.Item) bool {
return uint64(ii.cellID) < uint64(than.(IndexItem).cellID)
}
В данном примере у нас будут функции добавления полигона в индекс, поиска полигона, в котором мы находимся, и поиска ближайшего полигона.
func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error {}
func (i *Index) Search(lon, lat float64) ([]uint32, error) {}
func (i *Index) SearchNearest(lon, lat float64) ([]uint32, error) {}
Начнём с добавления полигона. Полигон задаётся списком вершин, причём S2 ожидает, что порядок вершин будет против часовой стрелки. Но в случае ошибки у нас будет функция «нормализации», которая как бы выворачивает его наизнанку.
func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error {
points := func() (res []s2.Point) {
for _, vertex := range vertices {
point := s2.PointFromLatLng(vertex)
res = append(res, point)
}
return
}()
loop := s2.LoopFromPoints(points)
loop.Normalize()
polygon := s2.PolygonFromLoops([]*s2.Loop{loop})
// ...
return nil
}
Список точек-вершин мы преобразуем в Loop, а затем и в полигон. Разница между ними в том, что полигон может состоять из нескольких loop-ов, иметь дырку, например, как пончик.
Как и в прошлом примере, мы попросим S2 покрыть наш полигон клетками и каждую из возвращённых клеток добавим в B-tree. Ну и в глобальный map.
func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error {
// ...
coverer := s2.RegionCoverer{MinLevel: i.storageLevel, MaxLevel: i.storageLevel}
cells := coverer.Covering(polygon)
for _, cell := range cells {
// ...
ii.polygonsInCell = append(ii.polygonsInCell, polygonID)
i.bt.ReplaceOrInsert(ii)
}
i.polygons[polygonID] = polygon
return nil
}
Функция поиска полигона, в котором мы находимся, в данном примере тривиальна. Как и раньше, преобразуем координату поиска в CellID на уровне storageLevel и находим или не находим эту клетку в B-дереве.
func (i *Index) Search(lon, lat float64) ([]uint32, error) {
latlng := s2.LatLngFromDegrees(lat, lon)
cellID := s2.CellIDFromLatLng(latlng)
cellIDOnStorageLevel := cellID.Parent(i.storageLevel)
item := i.bt.Get(IndexItem{cellID: cellIDOnStorageLevel})
if item != nil {
return item.(IndexItem).polygonsInCell, nil
}
return []uint32{}, nil
}
Поиск ближайшего полигона чуть сложнее. Сначала мы попробуем определить, вдруг мы уже находимся в каком-то полигоне. Если нет, то мы будем искать по увеличивающемуся радиусу (ниже я покажу, как это выглядит). Ну и когда мы найдём ближайшие полигоны, мы отфильтруем их и найдём самый ближайший, вычислив расстояние до каждого из найденных и взяв тот, расстояние до которого наименьшее.
func (i *Index) SearchNearest(lon, lat float64) ([]uint32, error) {
// ...
alreadyVisited := []s2.CellID{cellID}
var found []IndexItem
searched := []s2.CellID{cellID}
for {
found, searched = i.searchNextLevel(searched, &alreadyVisited)
if len(searched) == 0 {
break
}
if len(found) > 0 {
return i.filter(lon, lat, found), nil
}
}
return []uint32{}, nil
}
Что значит «по увеличивающемуся радиусу»? На первой картинке вы видите оранжевую клетку — центр нашего поиска. Сначала мы попробуем найти ближайший полигон во всех соседних клетках (на картинке они серые). Если мы ничего там не найдём, то отдалимся ещё на один уровень, как на второй картинке. И так далее.


«Соседей» нам даёт функция AllNeighbors. Разве что нужно полученные клетки отфильтровать и убрать те, которые мы уже просмотрели.
func (i *Index) searchNextLevel(radiusEdges []s2.CellID,
alreadyVisited *[]s2.CellID) (found []IndexItem, searched []s2.CellID) {
for _, radiusEdge := range radiusEdges {
neighbors := radiusEdge.AllNeighbors(i.storageLevel)
for _, neighbor := range neighbors {
if in(*alreadyVisited, neighbor) {
continue
}
*alreadyVisited = append(*alreadyVisited, neighbor)
searched = append(searched, neighbor)
item := i.bt.Get(IndexItem{cellID: neighbor})
if item != nil {
found = append(found, item.(IndexItem))
}
}
}
return
}
Вот, собственно, и всё. Для этого примера я также написал тест, и он успешно проходит.
Если вам интересно взглянуть на него или на полные примеры, то их можно найти здесь вместе со слайдами.
Заключение
Если вам когда-нибудь понадобится написать поисковый сервис, работающий с координатами или какими-то более сложными географическими объектами, и вы не захотите или не сможете использовать готовые СУБД типа PostGIS, вспомните об S2.
Это классный и простой инструмент, который даст вам базовые вещи и фреймворк для работы с координатами и земным шаром. Мы в Badoo очень любим S2 и всячески её рекомендуем.
Спасибо!
Upd: А вот и видео подоспело!