
Многие не знают, что некоторые сложные для написания и неэффективные для выполнения SQL-запросы можно легко выразить и эффективно выполнить в графовой базе данных. Это справедливо даже для тех, кто уже знает, что графовые алгоритмы являются наиболее эффективным, а иногда и единственным решением для сложных бизнес-задач, таких как кластеризация пользователей (с использованием Лувенского алгоритма), поиск инфлюенсеров - людей или компаний (алгоритмом PageRank) или прогнозирование поведения пользователей для персональных рекомендаций (алгоритмом label propagation).
В этой статье мы опишем SQL запрос с 24 JOIN в корпоративный knowledge graph и покажем, что задачу можно решить в графовой базе данных - и это будет понятней, более легко поддерживаться и эффективно выполняться. Пример взят из проблемы, описанной в сообществе: https://community.tigergraph.com/

Высокоуровневое описание бизнес-вопроса звучит следующим образом: найти Сущности, которые имеют по крайней мере три определенных Отношения с другими Сущностями, а связанные Сущности, в свою очередь, также должны иметь по крайней мере 3 других указанных Отношения. Более конкретно, проблема состоит в том, чтобы найти каждую отдельную сущность X такую, чтобы:
X имеет отношение типа R1 с сущностью A, которая имеет
отношение типа R1 к любому объекту, И
отношение типа R2 к любому объекту И
отношение типа R3 к любому объекту
И X имеет отношение типа R2 к сущности B, которая имеет
отношение типа R2 к любому объекту И
отношение типа R3 к любому объекту , И
отношение типа R4 к любому объекту
И X имеет отношение типа R3 к сущности C, которая имеет
отношение типа R3 к любому объекту , И
отношение типа R4 к любому объекту, И
отношение типа R5 к любому объекту
Каждое из 12 условий связывает одну сущность с другой. Все сущности хранятся в одной таблице, поэтому мы неоднократно возвращаемся к этой таблице. Кроме того, полная проблема имеет условия для значений атрибутов сущностей. Если мы предложим конкретный запрос, показывающий отдельные сущности, а не таблицы, то он может выглядеть следующим образом:
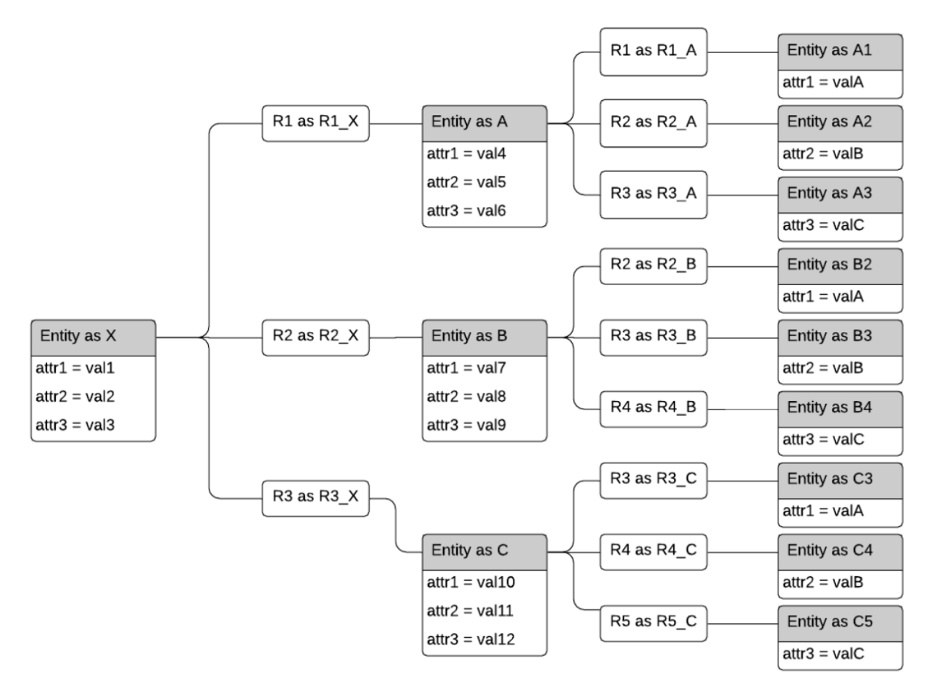
Этот запрос не настолько искусственен, как может показаться. Предположим, что сущности являются банковскими счетами, а отношения - это переводы с одного счета на другой. Такого рода древовидная схема может быть примером наслоения, метода, используемого при отмывании денег для сокрытия своей деятельности. Или это может быть отслеживанием Trickle-Down эффекта просачивания платежей, поступающих от сущности X - работодателя, фонда или государственного учреждения.
Этот контекст полезен для разработки и понимания SQL запроса, показаного ниже:
SELECT DISTINCT Entity.id
FROM Entity AS X
JOIN R1 AS R1_X ON Entity.id = R1_X.source
JOIN Entity AS A ON A.id = R1_X.target
JOIN R1 AS R1_A ON A.id = R1_A.source
JOIN R2 AS R2_A ON A.id = R2_A.source
JOIN R3 AS R3_A ON A.id = R3_A.source
JOIN Entity AS A1 ON R1_A.target = A1.id
JOIN Entity AS A2 ON R2_A.target = A2.id
JOIN Entity AS A3 ON R3_A.target = A3.id
JOIN R2 AS R2_X ON Entity.id = R2_X.source
JOIN Entity AS B ON B.id = R2_X.target
JOIN R2 AS R2_B ON B.id = R2_B.source
JOIN R3 AS R3_B ON B.id = R3_B.source
JOIN R4 AS R4_B ON B.id = R4_B.source
JOIN Entity AS B2 ON R2_B.target = B2.id
JOIN Entity AS B3 ON R3_B.target = B3.id
JOIN Entity AS B4 ON R4_B.target = B4.id
JOIN R3 AS R3_X ON Entity.id = R3_X.source
JOIN Entity AS C ON C.id = R3_X.target
JOIN R3 AS R3_C ON C.id = R3_C.source
JOIN R4 AS R4_C ON C.id = R4_C.source
JOIN R5 AS R5_C ON C.id = R5_C.source
JOIN Entity AS C3 ON R3_C.target = C3.id
JOIN Entity AS C4 ON R4_C.target = C4.id
JOIN Entity AS C5 ON R5_C.target = C5.id
WHERE
Entity.attr1 = val1 AND
Entity.attr2 = val2 AND
Entity.attr3 = val3 AND
A.attr1 = val4 AND
A.attr2 = val5 AND
A.attr3 = val6 AND
A1.attr1 = valA AND
A2.attr2 = valB AND
A3.attr3 = valC AND
B.attr1 = val7 AND
B.attr2 = val8 AND
B.attr3 = val9 AND
B2.attr1 = valA AND
B3.attr2 = valB AND
B4.attr3 = valC AND
C.attr1 = val10 AND
C.attr2 = val11 AND
C.attr3 = val12 AND
C3.attr1 = valA AND
C4.attr2 = valB AND
C5.attr3 = valCОбратите внимание, что в приведенном выше SQL-запросе к таблицам отношений содержится 12 JOIN'ов и еще 12 JOIN'ов (копий предыдущих) обратно к таблице Entity, а затем длинный набор условий для атрибутов различных сущностей.
Проблемы решения задачи с использованием SQL
Решение с 24 JOIN'нами в SQL сложно написать, понять и поддерживать. Фактически, у нас были значительные трудности с пониманием того, какая копия таблицы является какой, пока мы не сделали рисунок 2 с алиасами для каждой показанной таблицы. Также хорошо известно, что реляционным базам данных очень сложно выполнить несколько JOIN'ов в одном запросе. Такой запрос просто невозможен на больших таблицах.
Графовое решение со встроенным параллелизмом
Теперь мы покажем использование графовой базы данных со встроенным параллелизмом и графовым языком запросов, на примере TigerGraph и языком запросов GSQL, для простого и эффективного решения подобных проблем.
Сначала мы перерисуем схему и представим её в виде графа. На графе каждая Сущность становится вершиной, нарисованной кругом, а каждое Отношение становится ребром, нарисованным линией, соединяющей две Сущности. Ребра также могут иметь свойства, такие как время, местоположение или вес, но в данном примере рёбра не имеют свойств. Хотя схема выглядит по-другому, предлагаемое графовое решение - это просто другое представление реляционного решения.

Диаграмма схемы графа может выглядеть необычно, если вы не знакомы с графами. Схема говорит о том, что существует один тип Сущности, который имеет 3 атрибута (attr1, attr2 и attr3). Кроме того, существует пять типов Отношений — от R1 до R5 — каждое из которых соединяет Сущность с другой Сущностью с явным направлением.
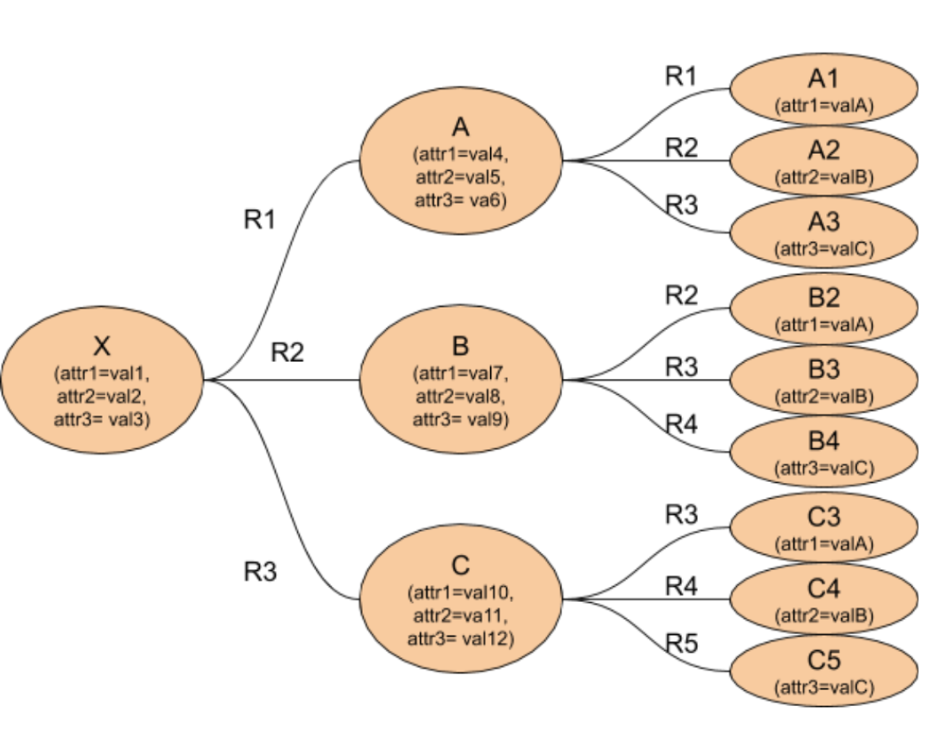
Благодаря мощности и гибкости GSQL, существуют различные подходы к решению этой задачи. Ниже показан один из таких способов.
/* Начинаем со всех элементов */
Entities = {Entity.*};
/* Вычисляем сущности A, подходящие по условиям атрибутов и нисходящим отношениям.
Сначала отношения R1, потом сужаем выборку до тех, где есть отношения R2 и R3 */
A = select m from Entities:m-(R1)-:t
where m.attr1 == val4 and m.attr2 == val5 and m.attr3 == val6
and t.attr1 == valA;
A = select m from A:m-(R2)-:t where t.attr2 == valB;
A = select m from A:m-(R3)-:t where t.attr3 == valC;
/* Вычисляем сущности B, подходящие по условиям атрибутов и нисходящим отношениям.
Сначала отношения R1, потом сужаем выборку до тех, где есть отношения R2 и R3 */
B = select m from Entities:m-(R2)-:t
where m.attr1 == val7 and m.attr2 == val8 and m.attr3 == val9
and t.attr1 == valA;
B = select m from B:m-(R3)-:t where t.attr2 == valB;
B = select m from B:m-(R4)-:t where t.attr3 == valC;
/* Вычисляем сущности C, подходящие по условиям атрибутов и нисходящим отношениям.
Сначала отношения R1, потом сужаем выборку до тех, где есть отношения R2 и R3 */
C = select m from Entities:m-(R3)-:t
where m.attr1 == val10 and m.attr2 == val11 and m.attr3 == val12
and t.attr1 == valA;
C = select m from C:m-(R4)-:t where t.attr2 == valB;
C = select m from C:m-(R5)-:t where t.attr3 == valC;
/* Вычисляем сущности X, подходящие по условиям атрибутов и нисходящим отношениям с A, B и C.
Сначала делаем выборку по атрибутам и связям R1, потом делаем выборки X где есть отношения R2 и R3 */
X1 = select t from A:s-(R1)-:t
where t.attr1 == val1 and t.attr2 == val2 and t.attr3 == val3;
X2 = select t from B:s-(R2)-:t;
X3 = select t from C:s-(R3)-:t;
/* Для конечного результата - делаем пересечение выборок X */
Result = X1 intersect X2 intersect X3;
print Result;Преимущества графового решения
Очевидно, что графовое решение намного проще в написании, чтении, понимании и сопровождении, чем один огромный SQL-запрос с 24 JOIN'нами. Графовое решение легко расширяется: позволяет выйти за рамки текущей "двухуровневой" проверки отношений без потери производительности и удобочитаемости.
Дальнейшее изучение
Один из лучших способов начать работу с графовой аналитикой - использовать TigerGraph Cloud. Это бесплатно, и можно создать учетную запись за несколько минут. Регистрируйтесь здесь.
Можно скачать сравнение производительности различных графовых баз данных: TigerGraph и Neo4j или TigerGraph и Amazon Neptune.
Вы также можете узнать больше о TigerGraph, присоединившись к нашему сообществу: https://community.tigergraph.com/.
Если хочется пообщаться на русском - пишите на TigerGraph@fgts.ru.
Мы с нетерпением ждем ваших экспериментов.