Здравствуй, Хабрахабр. Сейчас я хочу рассказать о такой структуре данных как дерево Фенвика. Впервые описанной Питером Фенвиком в 1994 году. Данная структура похожа на дерево отрезков, но проще в реализации.
Дерево Фенвика — это структура данных, дерево на массиве, которая обладает следующими свойствами:
• позволяет вычислять значение некоторой обратимой операции F на любом отрезке [L; R] за логарифмическое время;
• позволяет изменять значение любого элемента за O(log N);
• требует памяти O(N);
Операция F может быть выбрана разными способами, но чаще всего берутся операции суммы интервала, произведение интервала, а также при определенной модификации и ограничениях, нахождения максимума и нахождения минимума на интервале или другие операции.
Рассмотрим задачу о нахождения суммы последовательных элементов массива. С учетом того, что будет много запросов, вида (L,R), где требуется найти S(L,R)- сумму всех элементов с a[L] до a[R] включительно.
Простейшим решением данной задачи будет нахождение частичных сумм. После их нахождения запишем эти суммы в массив, в котором sum[i]=a[1]+a[2]...+a[i]. Тогда требуемая в запросе величина S(L,R)=sum[R]-sum[L-1] (sum[0] обычно считают равной нулю, чтобы не рассматривать отдельных случаев).
Но у данной реализации этой задачи есть существенные недостатки. И один из главных заключается в том, что при изменении одного элемента исходного массива, приходится пересчитывать в среднем O(N) частичных сумм, а это затратно по времени. Вот для решения этой проблемы можно использовать дерево Фенвика.
Главным преимуществом данной конструкции является простота реализации и быстрота ответов на запросы (за O(1)).
Введем функцию G(x), которая определена в натуральных числах, и равна x&(x+1) (&- побитовое И). Таким образом, G(x) равна x, если в двоичном разложении x последним стоит 0 (x делится на 2). А если в двоичном разложении x в младших разрядах идет группа единиц, то функция равна x с замененными последними единицами на 0. Можно убедиться на примерах, что это и есть x&(x+1) (смотрите рисунок).
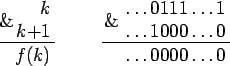
Теперь будем считать следующие частичные суммы, и записывать их в t[i]=a[G[i]]+a[G[i]+1]…+a[i]. Далее будет показано как находить эти суммы.
Чтобы найти S(L,R), будем искать S(1,L-1) и S(1,R). Напишем функцию, которая при наличии массива t, будет находить S(L,R). В данном случае левый конец не будет включен в сумму, но его легко включить если это требуется в задаче (смотрите код).
Так же стоит заметить, что функция G за каждое применение уменьшает количество единиц в двоичной записи x, как минимум на 1. Из чего следует, что подсчет суммы будет произведен за O(log N).
Теперь рассмотрим модификацию элементов. Нам надо научиться быстро изменять частичные суммы в зависимости от того, как изменяются элементы. Мы будем изменять a[k] на величину d. Тогда нам надо изменить элементы массива t[j], для которых верно неравенство G(j)<k<j. Но тут на помощь приходит следующий прием. Утверждается, что все искомые j будут принадлежать последовательности k[i] (смотрите выкладку).
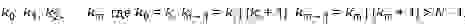
Где под | понимают побитовое ИЛИ.
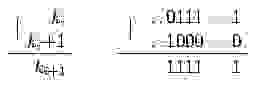
Несложно заметить, что данная функция строго возрастает и в худшем случае будет применена логарифм раз, так как добавляет каждый раз по одной единице в двоичном разложении числа k.
Напишем функцию, которая будет изменять a[k] элемент на d, и при этом меняет соответствующие частичные суммы.
Теперь заметим, что при первоначальном подсчете массива t, возможна его инициализация нулями. После чего, применяем для каждого из N элементов функцию upd(i,a[i]). Тогда, на первоначальный подсчет уйдет O(N*log N) времени, что больше чем у описанного алгоритма с простыми частичными суммами.
Преимущества:
— уже упомянутая простота и скорость
— памяти занимает O(N)
Недостатки:
— функция должна быть обратимой, а это значит, что минимум и максимум это дерево считать не может (за исключением случаев, когда некоторыми данными мы можем пожертвовать).
Мы научились отвечать на запросы о сумме элементов и модифицировать любой элемент за логарифмическое время. Данный алгоритм имеет множество применений, и может помочь во всех задачах, где надо быстро изменять и определять результат операции. Надеюсь, всем было понятно и интересно. Спасибо за внимание.
Что это?
Дерево Фенвика — это структура данных, дерево на массиве, которая обладает следующими свойствами:
• позволяет вычислять значение некоторой обратимой операции F на любом отрезке [L; R] за логарифмическое время;
• позволяет изменять значение любого элемента за O(log N);
• требует памяти O(N);
операция F
Операция F может быть выбрана разными способами, но чаще всего берутся операции суммы интервала, произведение интервала, а также при определенной модификации и ограничениях, нахождения максимума и нахождения минимума на интервале или другие операции.
Простейшая задача
Рассмотрим задачу о нахождения суммы последовательных элементов массива. С учетом того, что будет много запросов, вида (L,R), где требуется найти S(L,R)- сумму всех элементов с a[L] до a[R] включительно.
Простейшим решением данной задачи будет нахождение частичных сумм. После их нахождения запишем эти суммы в массив, в котором sum[i]=a[1]+a[2]...+a[i]. Тогда требуемая в запросе величина S(L,R)=sum[R]-sum[L-1] (sum[0] обычно считают равной нулю, чтобы не рассматривать отдельных случаев).
Недостатки
Но у данной реализации этой задачи есть существенные недостатки. И один из главных заключается в том, что при изменении одного элемента исходного массива, приходится пересчитывать в среднем O(N) частичных сумм, а это затратно по времени. Вот для решения этой проблемы можно использовать дерево Фенвика.
Преимущества
Главным преимуществом данной конструкции является простота реализации и быстрота ответов на запросы (за O(1)).
Применения дерева Фенвика для данной задачи
Введем функцию G(x), которая определена в натуральных числах, и равна x&(x+1) (&- побитовое И). Таким образом, G(x) равна x, если в двоичном разложении x последним стоит 0 (x делится на 2). А если в двоичном разложении x в младших разрядах идет группа единиц, то функция равна x с замененными последними единицами на 0. Можно убедиться на примерах, что это и есть x&(x+1) (смотрите рисунок).
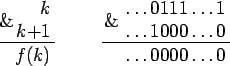
Теперь будем считать следующие частичные суммы, и записывать их в t[i]=a[G[i]]+a[G[i]+1]…+a[i]. Далее будет показано как находить эти суммы.
Подсчет суммы
Чтобы найти S(L,R), будем искать S(1,L-1) и S(1,R). Напишем функцию, которая при наличии массива t, будет находить S(L,R). В данном случае левый конец не будет включен в сумму, но его легко включить если это требуется в задаче (смотрите код).
const int N=100;
int t[N],a[N];
int sum(int L, int R)
{
int res=0;
while (R >= 0) {
res += t[R];
R = G( R ) - 1;
}
while (L >= 0) {
res -= t[L];
L = G(L) - 1;
}
return res;
}
Так же стоит заметить, что функция G за каждое применение уменьшает количество единиц в двоичной записи x, как минимум на 1. Из чего следует, что подсчет суммы будет произведен за O(log N).
Модификация элементов
Теперь рассмотрим модификацию элементов. Нам надо научиться быстро изменять частичные суммы в зависимости от того, как изменяются элементы. Мы будем изменять a[k] на величину d. Тогда нам надо изменить элементы массива t[j], для которых верно неравенство G(j)<k<j. Но тут на помощь приходит следующий прием. Утверждается, что все искомые j будут принадлежать последовательности k[i] (смотрите выкладку).

Где под | понимают побитовое ИЛИ.
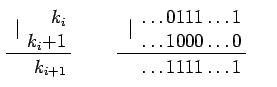
Несложно заметить, что данная функция строго возрастает и в худшем случае будет применена логарифм раз, так как добавляет каждый раз по одной единице в двоичном разложении числа k.
Напишем функцию, которая будет изменять a[k] элемент на d, и при этом меняет соответствующие частичные суммы.
const int N=100;
int t[N],a[N];
void upd(int k, int d)
{
a[k]+=d;
while(k<N)
{
t[k]+=d;
k=(k|(k+1));
}
}
Инициализация
Теперь заметим, что при первоначальном подсчете массива t, возможна его инициализация нулями. После чего, применяем для каждого из N элементов функцию upd(i,a[i]). Тогда, на первоначальный подсчет уйдет O(N*log N) времени, что больше чем у описанного алгоритма с простыми частичными суммами.
Сравнение с деревом отрезков
Преимущества:
— уже упомянутая простота и скорость
— памяти занимает O(N)
Недостатки:
— функция должна быть обратимой, а это значит, что минимум и максимум это дерево считать не может (за исключением случаев, когда некоторыми данными мы можем пожертвовать).
Заключение
Мы научились отвечать на запросы о сумме элементов и модифицировать любой элемент за логарифмическое время. Данный алгоритм имеет множество применений, и может помочь во всех задачах, где надо быстро изменять и определять результат операции. Надеюсь, всем было понятно и интересно. Спасибо за внимание.