Если вы пишете программы для кофемолок (холодильников, ZX Spectrum, телевизоров, встроенных систем, старых компьютеров — нужное подчеркнуть), и хотите использовать при этом красивые шрифты, не спешите сохранять буквы в растровый формат. Потому что сейчас я расскажу, как сделать растеризатор векторных шрифтов размером в пару килобайт, не уступающий по качеству FreeType 2 с выключенным хинтингом.
Статья будет интересна и тем, кто просто хочет узнать, как работают библиотеки-растеризаторы.
Чтобы сделать растеризатор, нужно сначала понять, как устроены векторные шрифты. Я выбрала в качестве основного формат шрифтов SVG потому, что он опирается на XML и является, пожалуй, самым читаемым и понятным для человека.
Первый шрифт, который я взяла для изучения — DejaVu Sans Mono Bold. Вот как он выглядит изнутри:
Главная часть формата SVG — это контуры (paths). В них хранится большая часть информации об изображении. Тег контура выглядит вот так:
Style описывает цвет заливки и обводки, id указывает имя контура, а d — это и есть сам контур.
Стоп… Минуточку! Тег glyph из шрифта:
Вот оно. Форма буквы (глифа) описывается точно так же, как и контуры SVG. Полное
описание параметра d можно найти в спецификации, а краткое описание привожу ниже:

x_prev и y_prev — координаты предыдущей точки
xc_prev и yc_prev — координаты предыдущей контрольной точки
Имея под рукой библиотеку для вывода кривых Безье и преобразовывая команды тега SVG path в команды этой библиотеки, можно легко и быстро получить аутлайн (обводку) любого глифа.
Глифы у нас векторные, а экран — растровый. Значит, задача вывода аутлайна сводится к получению из набора отрезков и кривых Безье массива пикселей. Отрезки превратить в пиксели очень легко, алгоритмов много, они хорошие и разные.
Для кривых Безье можно найти множество точек кривой по координатам начальной точки (xz0,yz0), конечной точки (xz2,yz2) и контрольной точки (xz1,yz1). Делается это вот так:
В результате имеем массив из 10 координат точек, принадлежащих кривой Безье. В зависимости от длины кривой из сложной системы дифференциальных уравнений находится количество точек, на которые нужно разбить кривую (то есть наибольшее значение step).
Однако превращать кривые Безье в пиксели по точкам — медленно и плохо. Если кривая сложной формы и большой длины, то расчет количества точек займет очень много времени. А если выводить кривую Безье по точкам, и этих точек окажется меньше, чем нужно — в аутлайне глифа будут разрывы, что недопустимо. Поэтому кривые Безье разбивают на отрезки. Начальные и конечные координаты отрезков берут как координаты точек, лежащих на кривой. В большей части случаев такое приближение дает хорошие результаты.
Как определить количество отрезков? Я считаю, достаточно делать максимальное значение step пропорциональным разнице между начальной и конечной координатами (например, step=(xz2-yz2)/100). Кстати, для всех шрифтов, которые я встречала, при высоте глифа менее 32 пикселов достаточно разбивать кривые Безье на два отрезка.
Результат работы растеризатора получится примерно такой:
Всё это хорошо, но на экране мы видим буквы, которые залиты цветом. Значит, как-то можно? Я потратила около двух месяцев на совершенствование алгоритмов заливки уже растрированного контура, и в конце концов убедилась, что такой подход является в корне неправильным. Для заливки векторных изображений растровая заливка не подходит.
В поисках решения этой веселой задачи я наткнулась на лекции MIT OCW по компьютерной графике. Меня заинтересовала лекция о растеризации трехмерной графики (а именно — треугольных полигонов). Суть метода заключалась в следующем: в векторном виде строилась проекция треугольного полигона на экран, и затем векторный треугольник закрашивался. Закрашивание производилось так: выбиралась область экрана, за которую треугольник однозначно не выходит, и для каждой точки этой области определялось, принадлежит ли она данному треугольнику. Та же лекция утверждает, что метод заливки Sweeping Line (который используют Cairo и FreeType) устарел, но об этом методе — чуть позже.
Осталось научиться определять, принадлежит ли точка контуру глифа, или не принадлежит. Контур глифа всегда замкнут. Значит, если мы проведем в любом направлении из любой точки луч, и он пересечет контур глифа нечетное число раз, то точка глифу принадлежит, а если четное — не принадлежит.
Интересно, что этот метод работает, даже если в контуре есть самопересечения или отверстия. Оказывается, данный алгоритм является хрестоматийным, и одна из его реализаций вот
такая:
Здесь xp и yp — массивы координат вершин многоугольника. Функция inPoly(x,y)
возвращает 1 или 0 — принадлежит точка многоугольнику или нет. Учитывая, что мы умеем
разбивать контур глифа на отрезки (то есть стороны многоугольника), то эта функция
замечательно нам подходит.
Теперь, переведя глиф в массив вершин xp и yp, мы можем написать простейший растеризатор. Пусть массив содержит отрезки с координатами от 0 до 2000. Тогда:
Эта простейшая функция создаст в массиве raster[x][y] растрированное изображение глифа. Выглядеть результат, выведенный на экран, будет примерно так (я вывела по очереди несколько глифов, и увеличил изображение примерно в 20 раз):

Глифы разрешением 2000x2000 пикселов на экране вряд ли кому-то нужны, да и алгоритм inPoly будет обрабатывать их довольно медленно. Чтобы вывести на экран глиф поменьше, сделаем примерно так:
Если scalefactor=2, то глиф будет выведен в квадрат 1000x1000 пикселов, а если scalefactor=100, то в квадрат 20x20 (вполне нормальный размер для экранных шрифтов).
Данный растеризатор выводит самые четкие (и самые неровные) очертания контуров, и ему сильнее всех других растеризаторов нужны алгоритмы хинтинга и контроля отсечки (они меняют форму контура в зависимости от разрешения). Для хранения одного растеризованного глифа в памяти необходимо x*y/8 байт. Полный набор символов ASCII займет в памяти не более x*y*32 байт (3200 байт для шрифта 10x10 и 8192 байт для шрифта 16x16). В процессе растеризации используется чуть больше, чем points*2*4 байт памяти (где points — количество точек в глифе, points как правило меньше 100, а иногда и меньше 10).
Гораздо лучший результат дает растеризация со сглаживанием. В библиотеке FreeType 1 использовалось
5ти-полутоновое сглаживание, сейчас в FreeType2 используется нечто более существенное (10ти- или 17ти-полутоновое сглаживание, я не вдавалась в подробности). Поэкспериментировав, я убедилась, что 10ти-полутоновое сглаживание значительно лучше, чем 5ти-полутоновое.
Здесь size — это размер глифа (в простом растеризаторе вместо size я подставляла 2000). Для хранения промежуточных данных используется массив landscape, а итоговый результат сохраняется в массив байт color[x][y].

Для вывода шрифтов на LCD-мониторах часто используют субпиксельное сглаживание. На обычных мониторах субпиксельное сглаживание дает результат почти такой же, как и обычное сглаживание, но на LCD сглаживание по субпикселям позволяет увеличить горизонтальное разрешение в три раза. Суть метода заключается в следующем: человеческий глаз гораздо лучше различает интенсивность, а не оттенок. Подробности есть во многих источниках, и даже на русской странице Википедии описание достаточное для практического использования.
Проблема простого субпиксельного сглаживания в том, что качество изображения на выходе ниже, чем у 10ти-полутонового алгоритма со сглаживанием. Для увеличения качества я использую четырехполутоновое сглаживание по вертикали, и субпиксельное — по горизонтали. Алгоритм субпиксельного сглаживания из справочников дает при этом вот такие ужасные результаты:
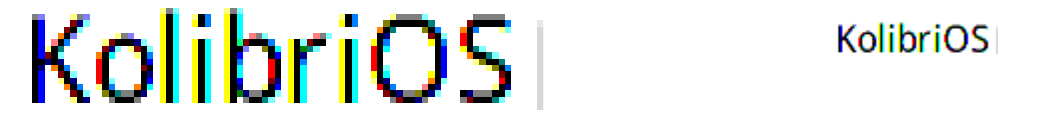
Чтобы избавиться от разноцветных «подтеков», я изменила коэффициенты размывания по
горизонтали, и вдобавок немного изменила гамму. Результат выглядит вот так (наилучшее
качество достигается при просмотре на LCD-мониторе):
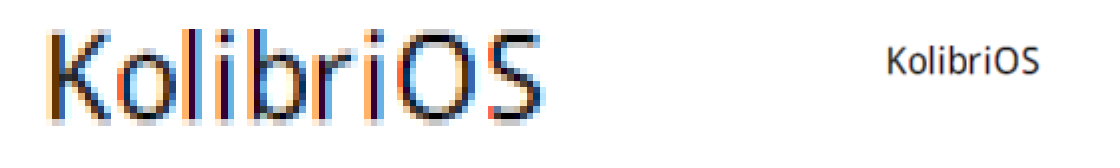
Посмотрим на алгоритм inPoly, про который я рассказывала, еще раз. Работает, но на больших символах работает медленно. Почему? Потому что скорость обработки пропорциональна квадрату size. Size вырос вдвое, скорость уменьшилась вчетверо, size вырос вчетверо — скорость упала в 16 раз.
Если немного посмотреть на алгоритм и подумать, можно обнаружить, что для каждой точки из тех, которые мы перебираем, испускается горизонтальный луч, и определяются его пересечения с контурами. Получается, что куча вычислений делается напрасно: для всех точек с одинаковой координатой Y уравнение горизонтальной прямой, проходящей через эти точки, будет одинаковым.
Раньше мы находили для каждой точки луч, и считали, сколько раз он пересекает контуры. Координаты пересечения мы находили, но не сохраняли. А теперь попробуем сделать вот что: будем находить луч только для точек (0,y), и сохранять координаты пересечения лучей с контурами.
Обращаю внимание:
1) Если часть контура горизонтальная и совпадает с заметающими линиями, то пересечения с этой частью контура не учитываются.
2) На одной заметающей всегда четное количество точек пересечения, потому что контур замкнут.
Остается лишь закрасить места между нечетными и четными точками, и оставить незакрашенными места межу четными и нечетными точками пересечения (при проходе линии слева направо). Шрифты должны быть хорошо спроектированы, и разрешение глифов не должно быть крохотным, тогда и качество страдать не будет.
Сравним скорость. Наш старый алгоритм должен был бы испустить лучи из 9x9 точек и найти координаты пересечения их с контурами. Новый алгоритм испустил всего 9 лучей — то есть он работает на порядок быстрее. И в то же время алгоритм sweeping line очень близок к тому алгоритму, что у нас был.
Итак, у нас есть функция inPoly. Сделаем из нее функцию sweep.
Очевидно, что входной параметр x больше не нужен. Функция sweep на входе получает только номер текущей строки. Зато пригодится входной параметр scale — чтобы получать x сразу в нужном масштабе.
Координату x пересечения текущей заметающей линии с некоторой прямой контура находили вот так:
То есть теперь будет:
На выходе функции мы должны получить массив из координат точек пересечения. Неплохо было бы узнать длину этого массива. Так что теперь будет не c = !c, а c++.
В итоге имеем вот что:
Итак, для каждой строки мы вызываем sweep, находим пересечения заметающей линии и по этим пересечениям заполняем массив. Однако, функция sweep может вернуть нам например вот такой массив координат:
14, 8, 16, 7
Чтобы правильно залить контур, нужно заполнять его линиями (7,y)-(8,y) и (14,y)-(16,y). Одним словом, нужно результаты функции sweep отсортировать. Хорошо работает quicksort, и с большим количеством координат желательно использовать его. Однако для шрифтов, которые у меня были под рукой, в массиве curline в основном было от 2 до 8 координат пересечений, и чтобы не усложнять себе жизнь, я использовала сортировку пузырьком. Моя функция bubble принимает на вход массив и его длину, ничего явно не возвращает, но массив становится отсортированным.
Перейдем непосредственно к растеризатору. Сначала нам нужно для каждой линии вызвать sweep, затем отсортировать массив curline командой bubble:
Массив начинается с 0 — поэтому нужно рисовать линии от curline[0+x] до curline[1+x]. Вот и всё. Мы получили массив landscape, и работать с ним нужно точно так же, как и раньше. То есть после этого его можно сгладить антиалиасингом или субпиксельным сглаживанием, или и тем, и другим. Главное — обратить внимание на то, что функции sweep тоже передается масштаб, он определяет растяжение по горизонтали.
Теперь вы знаете, как можно сделать растеризатор векторных шрифтов своими руками. Рабочий пример растеризатора можно скачать здесь, но он написан для операционной системы Колибри (так что вам и ее придется скачать, если хотите запустить этот пример). Размер скомпилированной программы — 2589 байт, максимальное использование ОЗУ — около 300 килобайт. И это не предел!
Статья будет интересна и тем, кто просто хочет узнать, как работают библиотеки-растеризаторы.
Векторные шрифты в формате SVG
Чтобы сделать растеризатор, нужно сначала понять, как устроены векторные шрифты. Я выбрала в качестве основного формат шрифтов SVG потому, что он опирается на XML и является, пожалуй, самым читаемым и понятным для человека.
Первый шрифт, который я взяла для изучения — DejaVu Sans Mono Bold. Вот как он выглядит изнутри:
<?xml version="1.0" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/REC-
SVG-20010904/DTD/svg10.dtd">
<svg xmlns="www.w3.org/2000/svg" width="100%" height="100%">
<defs >
<font horiz-adv-x="1233" ><font-face
font-family="DejaVu Sans Mono"
units-per-em="2048"
panose-1="2 11 7 9 3 6 4 2 2 4"
ascent="1901"
descent="-483"
alphabetic="0" />
<glyph unicode=" " glyph-name="space" />
<glyph unicode="$" glyph-name="dollar" d=" M 694 528 V 226 Q 757 235 792 274 T
827 375 Q 827 437 793 476 T 694 528 Z M 553 817 V 1100 Q 491 1092 460 1059 T 428
967 Q 428 910 459 872 T 553 817 Z M 694 -301 H 553 L 552 0 Q 465 3 370 26 T 172
92 V 354 Q 275 293 371 260 T 553 226 V 555 Q 356
594 260 689 T 164 942 Q 164 1109 266 1208 T 553 1319 V 1556 H 694 L 695 1319 Q
766 1315 842 1301 T 999 1262 V 1006 Q 937 1046 861 1070 T 694 1100 V 793 Q 891
762 991 659 T 1092 383 Q 1092 219 984 114 T 695 0 L 694 -301 Z " />
<!-- … опущено.... -->
<glyph unicode="~" glyph-name="asciitilde" d=" M 1145 811 V 578 Q 1070 518 999
491 T 848 463 Q 758 463 645 514 Q 623 524 612 528 Q 535 562 484 574 T 381 586 Q
303 586 233 557 T 88 465 V 694 Q 166 755 239 782 T 395 809 Q 448 809 498 798 T
622 756 Q 633 751 655 741 Q 771 686 864
686 Q 934 686 1003 716 T 1145 811 Z " />
</font>
</defs>
</svg>
Главная часть формата SVG — это контуры (paths). В них хранится большая часть информации об изображении. Тег контура выглядит вот так:
<path
d=" M 1145 811 V 578 Q 1070 518 999 491 T 848 463 Q 758 463 645 514 Q 623
524 612 528 Q 535 562 484 574 T 381 586 Q 303 586 233 557 T 88 465 V 694 Q 166
755 239 782 T 395 809 Q 448 809 498 798 T 622 756 Q 633 751 655 741 Q 771 686
864 686 Q 934 686 1003 716 T 1145 811 Z "
id="path4840"
style="fill:#000000;stroke:#000000;stroke-width:1px;stroke-
linecap:butt;stroke-linejoin:miter;stroke-opacity:1" />Style описывает цвет заливки и обводки, id указывает имя контура, а d — это и есть сам контур.
Стоп… Минуточку! Тег glyph из шрифта:
<glyph unicode="~" glyph-name="asciitilde" d=" M 1145 811 V 578 Q 1070 518 999
491 T 848 463 Q 758 463 645 514 Q 623 524 612 528 Q 535 562 484 574 T 381 586 Q
303 586 233 557 T 88 465 V 694 Q 166 755 239 782 T 395 809 Q 448 809 498 798 T
622 756 Q 633 751 655 741 Q 771 686 864 686 Q 934 686 1003 716 T 1145 811 Z " />Вот оно. Форма буквы (глифа) описывается точно так же, как и контуры SVG. Полное
описание параметра d можно найти в спецификации, а краткое описание привожу ниже:

x_prev и y_prev — координаты предыдущей точки
xc_prev и yc_prev — координаты предыдущей контрольной точки
Outline (обводка) глифа и начальная растеризация
Имея под рукой библиотеку для вывода кривых Безье и преобразовывая команды тега SVG path в команды этой библиотеки, можно легко и быстро получить аутлайн (обводку) любого глифа.
Глифы у нас векторные, а экран — растровый. Значит, задача вывода аутлайна сводится к получению из набора отрезков и кривых Безье массива пикселей. Отрезки превратить в пиксели очень легко, алгоритмов много, они хорошие и разные.
Для кривых Безье можно найти множество точек кривой по координатам начальной точки (xz0,yz0), конечной точки (xz2,yz2) и контрольной точки (xz1,yz1). Делается это вот так:
for (step=0;step<10;step++) {
t=step/10;
bx[step]=(1-t)*(1-t)*xz0+2*t*(1-t)*xz1+t*t*xz2;
by[step]=(1-t)*(1-t)*yz0+2*t*(1-t)*yz1+t*t*yz2;
}В результате имеем массив из 10 координат точек, принадлежащих кривой Безье. В зависимости от длины кривой из сложной системы дифференциальных уравнений находится количество точек, на которые нужно разбить кривую (то есть наибольшее значение step).
Однако превращать кривые Безье в пиксели по точкам — медленно и плохо. Если кривая сложной формы и большой длины, то расчет количества точек займет очень много времени. А если выводить кривую Безье по точкам, и этих точек окажется меньше, чем нужно — в аутлайне глифа будут разрывы, что недопустимо. Поэтому кривые Безье разбивают на отрезки. Начальные и конечные координаты отрезков берут как координаты точек, лежащих на кривой. В большей части случаев такое приближение дает хорошие результаты.
Как определить количество отрезков? Я считаю, достаточно делать максимальное значение step пропорциональным разнице между начальной и конечной координатами (например, step=(xz2-yz2)/100). Кстати, для всех шрифтов, которые я встречала, при высоте глифа менее 32 пикселов достаточно разбивать кривые Безье на два отрезка.
Результат работы растеризатора получится примерно такой:
Заливка контура глифа — главный этап растеризации
Всё это хорошо, но на экране мы видим буквы, которые залиты цветом. Значит, как-то можно? Я потратила около двух месяцев на совершенствование алгоритмов заливки уже растрированного контура, и в конце концов убедилась, что такой подход является в корне неправильным. Для заливки векторных изображений растровая заливка не подходит.
В поисках решения этой веселой задачи я наткнулась на лекции MIT OCW по компьютерной графике. Меня заинтересовала лекция о растеризации трехмерной графики (а именно — треугольных полигонов). Суть метода заключалась в следующем: в векторном виде строилась проекция треугольного полигона на экран, и затем векторный треугольник закрашивался. Закрашивание производилось так: выбиралась область экрана, за которую треугольник однозначно не выходит, и для каждой точки этой области определялось, принадлежит ли она данному треугольнику. Та же лекция утверждает, что метод заливки Sweeping Line (который используют Cairo и FreeType) устарел, но об этом методе — чуть позже.
Осталось научиться определять, принадлежит ли точка контуру глифа, или не принадлежит. Контур глифа всегда замкнут. Значит, если мы проведем в любом направлении из любой точки луч, и он пересечет контур глифа нечетное число раз, то точка глифу принадлежит, а если четное — не принадлежит.
Интересно, что этот метод работает, даже если в контуре есть самопересечения или отверстия. Оказывается, данный алгоритм является хрестоматийным, и одна из его реализаций вот
такая:
xp = new Array (10, 20, 30, 40);
yp = new Array (30, 40, 20, 10);
function inPoly(x,y){
npol = xp.length;
j = npol - 1;
var c = 0;
for (i = 0; i < npol;i++){
if ((((yp[i]<=y) && (y<yp[j])) || ((yp[j]<=y) && (y<yp[i]))) &&
(x > (xp[j] - xp[i]) * (y - yp[i]) / (yp[j] - yp[i]) + xp[i])) {
c = !c;}
j = i;}
return c;}Здесь xp и yp — массивы координат вершин многоугольника. Функция inPoly(x,y)
возвращает 1 или 0 — принадлежит точка многоугольнику или нет. Учитывая, что мы умеем
разбивать контур глифа на отрезки (то есть стороны многоугольника), то эта функция
замечательно нам подходит.
Простейший растеризатор
Теперь, переведя глиф в массив вершин xp и yp, мы можем написать простейший растеризатор. Пусть массив содержит отрезки с координатами от 0 до 2000. Тогда:
function simple(){
for (x=0;x<2000;x++) {
for (y=0;y<2000;y++) {
if (inPoly(x,y)>0) raster[x][y]=1;}}}Эта простейшая функция создаст в массиве raster[x][y] растрированное изображение глифа. Выглядеть результат, выведенный на экран, будет примерно так (я вывела по очереди несколько глифов, и увеличил изображение примерно в 20 раз):

Глифы разрешением 2000x2000 пикселов на экране вряд ли кому-то нужны, да и алгоритм inPoly будет обрабатывать их довольно медленно. Чтобы вывести на экран глиф поменьше, сделаем примерно так:
function simple(scalefactor){
for (x=0;x<2000/scalefactor;x++) {
for (y=0;y<2000/scalefactor;y++) {
if (inPoly(x*scalefactor,y*scalefactor)>0) raster[x][y]=1;}}}Если scalefactor=2, то глиф будет выведен в квадрат 1000x1000 пикселов, а если scalefactor=100, то в квадрат 20x20 (вполне нормальный размер для экранных шрифтов).
Данный растеризатор выводит самые четкие (и самые неровные) очертания контуров, и ему сильнее всех других растеризаторов нужны алгоритмы хинтинга и контроля отсечки (они меняют форму контура в зависимости от разрешения). Для хранения одного растеризованного глифа в памяти необходимо x*y/8 байт. Полный набор символов ASCII займет в памяти не более x*y*32 байт (3200 байт для шрифта 10x10 и 8192 байт для шрифта 16x16). В процессе растеризации используется чуть больше, чем points*2*4 байт памяти (где points — количество точек в глифе, points как правило меньше 100, а иногда и меньше 10).
Анти-алиасинг (сглаживание)
Гораздо лучший результат дает растеризация со сглаживанием. В библиотеке FreeType 1 использовалось
5ти-полутоновое сглаживание, сейчас в FreeType2 используется нечто более существенное (10ти- или 17ти-полутоновое сглаживание, я не вдавалась в подробности). Поэкспериментировав, я убедилась, что 10ти-полутоновое сглаживание значительно лучше, чем 5ти-полутоновое.
function aadraw(scalefactor){
//Мы растеризуем изображение в девять (3*3) раз больше, чем хотим получить
for (x=0;x<size*3/scalefactor;x++) {
for (y=0;y<size*3/scalefactor;y++) {
if (inpoly(x*scalefactor/3,y*scalefactor/3)>0) landscape[x][y]=1;}}
//Затем уменьшаем его в три раза с примитивным сглаживанием
for (x=0;x<size/scalefactor;x++) {
for (y=0;y<size/scalefactor;y++) {
//определяем цвет точки, он будет лежать в диапазоне от 00 до FF
color[x][y]=255-28*(landscape[x*3][y*3]+landscape[x*3][y*3+1]+landscape[x*3][y*3+2]+landscape[x*3+1][y*3]+landscape[x*3+1][y*3+1]+landscape[x*3+1][y*3+2]+landscape[x*3+2][y*3]+landscape[x*3+2][y*3+1]+landscape[x*3+2][y*3+2]));}}//Конец уменьшения
}//Конец функцииЗдесь size — это размер глифа (в простом растеризаторе вместо size я подставляла 2000). Для хранения промежуточных данных используется массив landscape, а итоговый результат сохраняется в массив байт color[x][y].

Субпиксельное сглаживание
Для вывода шрифтов на LCD-мониторах часто используют субпиксельное сглаживание. На обычных мониторах субпиксельное сглаживание дает результат почти такой же, как и обычное сглаживание, но на LCD сглаживание по субпикселям позволяет увеличить горизонтальное разрешение в три раза. Суть метода заключается в следующем: человеческий глаз гораздо лучше различает интенсивность, а не оттенок. Подробности есть во многих источниках, и даже на русской странице Википедии описание достаточное для практического использования.
Проблема простого субпиксельного сглаживания в том, что качество изображения на выходе ниже, чем у 10ти-полутонового алгоритма со сглаживанием. Для увеличения качества я использую четырехполутоновое сглаживание по вертикали, и субпиксельное — по горизонтали. Алгоритм субпиксельного сглаживания из справочников дает при этом вот такие ужасные результаты:

Чтобы избавиться от разноцветных «подтеков», я изменила коэффициенты размывания по
горизонтали, и вдобавок немного изменила гамму. Результат выглядит вот так (наилучшее
качество достигается при просмотре на LCD-мониторе):

function xdraw(scalefactor){
//Нам нужно изображение в шесть (3*2) раз больше, чем мы хотим получить
for (x=0;x<size*3/scalefactor;x++) {
for (y=0;y<size*2/scalefactor;y++) {
if (inpoly(x*scalefactor/3,y*scalefactor/2)>0) landscape[x][y]=1;}}
//Применим к этому изображению стандартное размытие перед разбивкой на субпиксели
for (x=0;x<size*3/scalefactor;x++) {
for (y=0;y<size*2/scalefactor;y++) {
if (x>2 && x<size*3/scalefactor-2) landscape1[x][y]=landscape[x-2][y]*(1/9)+landscape[x+2][y]*(1/9)+landscape[x-1][y]*(2/9)+landscape[x+1][y]*(2/9)+landscape[x][y]*(1/3)}}
//Теперь сожмем изображение в два раза, с применением нелинейного размытия
for (x=0;x<size*3/scalefactor;x++) {
for (y=1;y<size/scalefactor;y++) {
landscape2[x][y]=landscape1[x][y*2-1]*(2/9)+landscape1[x][y*2+1]*(2/9)+landscape1[x][y*2]*(4/9);
if (landscape2[x][y]==8/9) landscape2[x][y]=1;}} //и подкорректируем гамму
//Распилим картинку на субпиксели
for (x=0;x<size/scalefactor;x++) {
for (y=0;y<size/scalefactor;y++) {
r[x][y]=Math.floor(255-255*landscape2[x*3][y]);g[x][y]=Math.floor(255-255*landscape2[x*3+1][y]);b[x][y]=Math.floor(255-255*landscape2[x*3+2][y]);}}
}//Конец функции
Метод заметающей линии (sweeping line). Основная идея
Посмотрим на алгоритм inPoly, про который я рассказывала, еще раз. Работает, но на больших символах работает медленно. Почему? Потому что скорость обработки пропорциональна квадрату size. Size вырос вдвое, скорость уменьшилась вчетверо, size вырос вчетверо — скорость упала в 16 раз.
Если немного посмотреть на алгоритм и подумать, можно обнаружить, что для каждой точки из тех, которые мы перебираем, испускается горизонтальный луч, и определяются его пересечения с контурами. Получается, что куча вычислений делается напрасно: для всех точек с одинаковой координатой Y уравнение горизонтальной прямой, проходящей через эти точки, будет одинаковым.
Раньше мы находили для каждой точки луч, и считали, сколько раз он пересекает контуры. Координаты пересечения мы находили, но не сохраняли. А теперь попробуем сделать вот что: будем находить луч только для точек (0,y), и сохранять координаты пересечения лучей с контурами.
Обращаю внимание:
1) Если часть контура горизонтальная и совпадает с заметающими линиями, то пересечения с этой частью контура не учитываются.
2) На одной заметающей всегда четное количество точек пересечения, потому что контур замкнут.
Остается лишь закрасить места между нечетными и четными точками, и оставить незакрашенными места межу четными и нечетными точками пересечения (при проходе линии слева направо). Шрифты должны быть хорошо спроектированы, и разрешение глифов не должно быть крохотным, тогда и качество страдать не будет.
Сравним скорость. Наш старый алгоритм должен был бы испустить лучи из 9x9 точек и найти координаты пересечения их с контурами. Новый алгоритм испустил всего 9 лучей — то есть он работает на порядок быстрее. И в то же время алгоритм sweeping line очень близок к тому алгоритму, что у нас был.
Sweeping line. Изменения в коде inPoly
Итак, у нас есть функция inPoly. Сделаем из нее функцию sweep.
function inPoly(x,y){
npol = xp.length;
j = npol - 1;
var c = 0;
for (i = 0; i < npol;i++){
if ((((yp[i]<=y) && (y<yp[j])) || ((yp[j]<=y) && (y<yp[i]))) &&
(x > (xp[j] - xp[i]) * (y - yp[i]) / (yp[j] - yp[i]) + xp[i])) {
c = !c;}
j = i;}
return c;}Очевидно, что входной параметр x больше не нужен. Функция sweep на входе получает только номер текущей строки. Зато пригодится входной параметр scale — чтобы получать x сразу в нужном масштабе.
Координату x пересечения текущей заметающей линии с некоторой прямой контура находили вот так:
(x >(xp[j]- xp[i])*(y - yp[i])/(yp[j]- yp[i])+ xp[i]))То есть теперь будет:
x =(xp[j]- xp[i])*(y - yp[i])/(yp[j]- yp[i])+ xp[i])На выходе функции мы должны получить массив из координат точек пересечения. Неплохо было бы узнать длину этого массива. Так что теперь будет не c = !c, а c++.
В итоге имеем вот что:
function sweep(y,scale){
npol = xp.length; //все как обычно....
j = npol -1;
var c =0;
for(i =0; i < npol;i++){
if(((yp[i]<=y)&&(y<yp[j]))||((yp[j]<=y)&&(y<yp[i])))
{ x =(xp[j]- xp[i])*(y - yp[i])/(yp[j]- yp[i])+ xp[i];
curline[c]=x/scale; c++;} //только теперь условия меньше, а точки пересечения сохраняются в массив
j = i;}
return c;} //пусть функция возвращает количество пересечений
И снова — простой растеризатор
Итак, для каждой строки мы вызываем sweep, находим пересечения заметающей линии и по этим пересечениям заполняем массив. Однако, функция sweep может вернуть нам например вот такой массив координат:
14, 8, 16, 7
Чтобы правильно залить контур, нужно заполнять его линиями (7,y)-(8,y) и (14,y)-(16,y). Одним словом, нужно результаты функции sweep отсортировать. Хорошо работает quicksort, и с большим количеством координат желательно использовать его. Однако для шрифтов, которые у меня были под рукой, в массиве curline в основном было от 2 до 8 координат пересечений, и чтобы не усложнять себе жизнь, я использовала сортировку пузырьком. Моя функция bubble принимает на вход массив и его длину, ничего явно не возвращает, но массив становится отсортированным.
Перейдем непосредственно к растеризатору. Сначала нам нужно для каждой линии вызвать sweep, затем отсортировать массив curline командой bubble:
for(y=0;y<size/scale;y++){ //нам больше не нужен вложенный цикл для всех x
every=sweep(y*scale, scale); //every — это количество элементов массива
bubble(curline,every); //сортируем массив
for(point=0;point<every;point=point+2){ //для всех точек массива
for(x=curline[point];x<curline[point+1];x++){landscape[x][y]=1;}
//рисуем линии точками
}}//заканчиваем цикл и функциюМассив начинается с 0 — поэтому нужно рисовать линии от curline[0+x] до curline[1+x]. Вот и всё. Мы получили массив landscape, и работать с ним нужно точно так же, как и раньше. То есть после этого его можно сгладить антиалиасингом или субпиксельным сглаживанием, или и тем, и другим. Главное — обратить внимание на то, что функции sweep тоже передается масштаб, он определяет растяжение по горизонтали.
Результаты работы
Теперь вы знаете, как можно сделать растеризатор векторных шрифтов своими руками. Рабочий пример растеризатора можно скачать здесь, но он написан для операционной системы Колибри (так что вам и ее придется скачать, если хотите запустить этот пример). Размер скомпилированной программы — 2589 байт, максимальное использование ОЗУ — около 300 килобайт. И это не предел!