 В заметке обсуждаются алгоритмы решета для поиска простых чисел. Мы подробно рассмотрим классическое решето Эратосфена, особенности его реализации на популярных языках программирования, параллелизацию и оптимизацию, а затем опишем более современное и быстрое решето Аткина. Если материал о решете Эратосфена предназначен в первую очередь уберечь новичков от регулярного хождения по граблям, то алгоритм решета Аткина ранее на Хабрахабре не описывался.
В заметке обсуждаются алгоритмы решета для поиска простых чисел. Мы подробно рассмотрим классическое решето Эратосфена, особенности его реализации на популярных языках программирования, параллелизацию и оптимизацию, а затем опишем более современное и быстрое решето Аткина. Если материал о решете Эратосфена предназначен в первую очередь уберечь новичков от регулярного хождения по граблям, то алгоритм решета Аткина ранее на Хабрахабре не описывался.На снимке — скульптура абстрактного экспрессиониста Марка Ди Суверо «Решето Эратосфена», установленная в кампусе Стэнфорского университета
Введение
Напомним, что число называется простым, если оно имеет ровно два различных делителя: единицу и самого себя. Числа, имеющие большее число делителей, называются составными. Таким образом, если мы умеем раскладывать числа на множители, то мы умеем и проверять числа на простоту. Например, как-то так:
function isprime(n){
if(n==1) // 1 - не простое число
return false;
// перебираем возможные делители от 2 до sqrt(n)
for(d=2; d*d<=n; d++){
// если разделилось нацело, то составное
if(n%d==0)
return false;
}
// если нет нетривиальных делителей, то простое
return true;
}
Время работы такого теста, очевидно, есть O(n½), т. е. растет экспоненциально относительно битовой длины n. Этот тест называется проверкой перебором делителей.
Довольно неожиданно, что существует ряд способов проверить простоту числа, не находя его делителей. Если полиномиальный алгоритм разложения на множители пока остается недостижимой мечтой (на чем и основана стойкость шифрования RSA), то разработанный в 2004 году тест на простоту AKS [1] отрабатывает за полиномиальное время. С различными эффективными тестами на простоту можно ознакомиться по [2].
Если теперь нам нужно найти все простые на достаточно широком интервале, то первым побуждением, наверное, будет протестировать каждое число из интервала индивидуально. К счастью, если у нас достаточно памяти, можно использовать более быстрые (и простые) алгоритмы решета. В этой статье мы обсудим два из них: классическое решето Эратосфена, известное еще древним грекам, и решето Аткина, наиболее совершенный современный алгоритм этого семейства.
Решето Эратосфена
Древнегреческий математик Эратосфен предложил следующий алгоритм для нахождения всех простых, не превосходящих данного числа n. Возьмем массив S длины n и заполним его единицами (пометим как невычеркнутые). Теперь будем последовательно просматривать элементы S[k], начиная с k = 2. Если S[k] = 1, то заполним нулями (вычеркнем или высеем) все последующие ячейки, номера которых кратны k. В результате получим массив, в котором ячейки содержат 1 тогда и только тогда, когда номер ячейки — простое число.
Много времени можно сэкономить, если заметить, что, поскольку у составного числа, меньшего n, по крайней мере один из делителей не превосходит
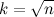 . Вот анимация решета Эратосфена, взятая с Википедии:
. Вот анимация решета Эратосфена, взятая с Википедии:
Еще немного операций можно сэкономить, если — по той же причине — начинать вычеркивать кратные k, начиная не с 2k, а с номера k2.
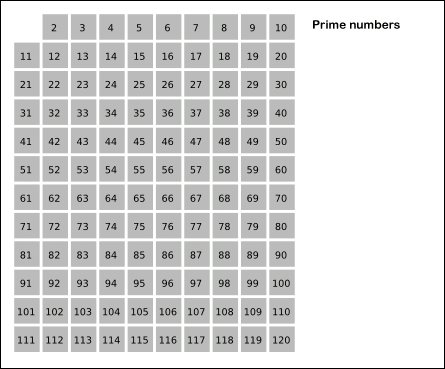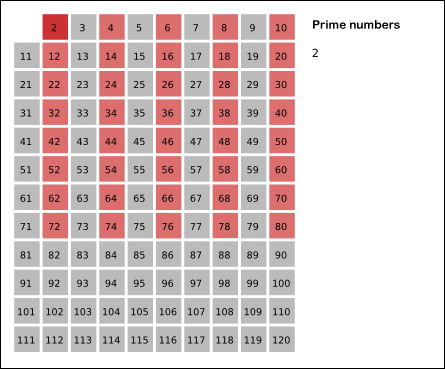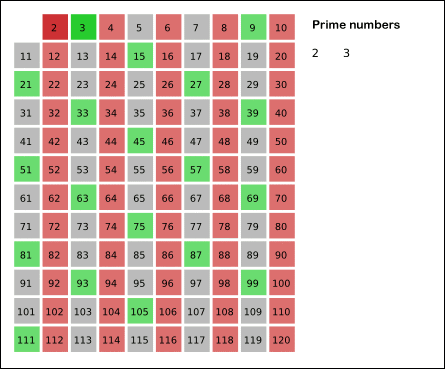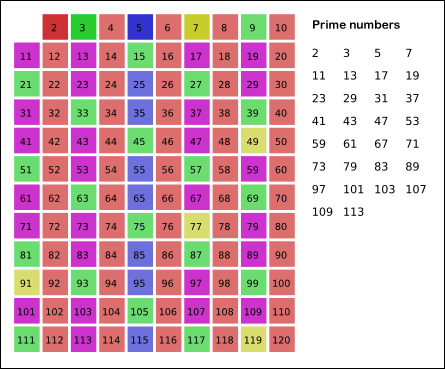
Реализация примет следующий вид:
function sieve(n){
S = [];
S[1] = 0; // 1 - не простое число
// заполняем решето единицами
for(k=2; k<=n; k++)
S[k]=1;
for(k=2; k*k<=n; k++){
// если k - простое (не вычеркнуто)
if(S[k]==1){
// то вычеркнем кратные k
for(l=k*k; l<=n; l+=k){
S[l]=0;
}
}
}
return S;
}
Эффективность решета Эратосфена вызвана крайней простотой внутреннего цикла: он не содержит условных переходов, а также «тяжелых» операций вроде деления и умножения.
Оценим сложность алгоритма. Первое вычеркивание требует n/2 действий, второе — n/3, третье — n/5 и т. д. По формуле Мертенса
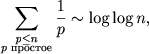
так что для решета Эратосфена потребуется O(n log log n) операций. Потребление памяти же составит O(n).
Оптимизация и параллелизация
Первую оптимизацию решета предложил сам Эратосфен: раз из всех четных чисел простым является только 2, то давайте сэкономим половину памяти и времени и будем выписывать и высеивать только нечетные числа. Реализация такой модификации алгоритма потребует лишь косметических изменений (код).
Более развитая оптимизация (т. н. wheel factorization) опирается на то, что все простые, кроме 2, 3 и 5, лежат в одной из восьми следующих арифметических прогрессий: 30k+1, 30k+7, 30k+11, 30k+13, 30k+17, 30k+19, 30k+23 и 30k+29. Чтобы найти все простые числа до n, вычислим предварительно (опять же при помощи решета) все простые до
Наращивая шаг прогрессии и количество решет (например, при шаге прогрессии 210 нам понадобится 48 решет, что сэкономит еще 4% ресурсов) параллельно росту n, удается увеличить скорость алгоритма в log log n раз.
Сегментация
Что же делать, если, несмотря на все наши ухищрения, оперативной памяти не хватает и алгоритм безбожно «свопится»? Можно заменить одно большое решето на последовательность маленьких ситечек и высевать каждое в отдельности. Как и выше, нам придется предварительно подготовить список простых до
Не надо делать ситечки слишком маленькими, меньше тех же O(n½-ε) элементов. Так вы ничего не выиграете в асимптотике потребления памяти, но из-за накладных расходов начнете все сильнее терять в производительности.
Решето Эратосфена и однострочники
На Хабрахабре ранее публиковалась большая подборка алгоритмов Эратосфена в одну строчку на разных языках программирования (однострочники №10). Интересно, что все они на самом деле решетом Эратосфена не являются и реализуют намного более медленные алгоритмы.
Дело в том, что фильтрация множества по условию (например,
primes = primes.select { |x| x == prime || x % prime != 0 } let pgen (p:xs) = p : pgen [x|x <- xs, x `mod` p > 0] 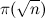 (это число фильтраций), умноженного на
(это число фильтраций), умноженного на 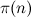 (минимальное число элементов фильтруемого множества), где
(минимальное число элементов фильтруемого множества), где 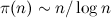 — число простых, не превосходящих n, т. е. до O(n3/2-ε) действий.
— число простых, не превосходящих n, т. е. до O(n3/2-ε) действий. Однострочник
(n: Int) => (2 to n) |> (r => r.foldLeft(r.toSet)((ps, x) => if (ps(x)) ps -- (x * x to n by x) else ps))Вообще решето Эратосфена тяжело эффективно реализовать в рамках функциональной парадигмы неизменяемых переменных. В случае, если функциональный язык (например, OСaml) позволяет, стоит нарушить нормы и завести изменяемый массив. В [3] обсуждается, как грамотно реализовать решето Эратосфена на Haskell при помощи техники ленивых вычеркиваний.
Решето Эратосфена и PHP
Запишем алгоритм Эратосфена на PHP. Получится примерно следующее:
define("LIMIT",1000000);
define("SQRT_LIMIT",floor(sqrt(LIMIT)));
$S = array_fill(2,LIMIT-1,true);
for($i=2;$i<=SQRT_LIMIT;$i++){
if($S[$i]===true){
for($j=$i*$i; $j<=LIMIT; $j+=$i){
$S[$j]=false;
}
}
}
Здесь есть две проблемы. Первая из них связана с системой типов данных и является характерной для многих современных языков. Дело в том, что наиболее эффективно решето Эратосфена реализуется в тех ЯП, где можно объявить гомогенный массив, последовательно расположенный в памяти. Тогда вычисление адреса ячейки S[i] займет всего пару команд процессора. Массив же в PHP — это на самом деле гетерогенный словарь, т. е. он индексируется произвольными строками или числами и может содержать данные различных типов. В таком случае нахождение S[i] становится куда более трудооемкой задачей.
Вторая проблема: массивы в PHP ужасны по накладным расходам памяти. У меня на 64-битной системе каждый элемент $S из кода выше съедает по 128 байт. Как обсуждалось выше, необязательно держать сразу все решето в памяти, можно обрабатывать его порционно, но все равно такие расходы дóлжно признать недопустимыми.
Для решения этих проблем достаточно выбрать более подходящий тип данных — строку!
define("LIMIT",1000000);
define("SQRT_LIMIT",floor(sqrt(LIMIT)));
$S = str_repeat("\1", LIMIT+1);
for($i=2;$i<=SQRT_LIMIT;$i++){
if($S[$i]==="\1"){
for($j=$i*$i; $j<=LIMIT; $j+=$i){
$S[$j]="\0";
}
}
}
Теперь каждый элемент занимает ровно 1 байт, а время работы уменьшилось примерно втрое. Скрипт для измерения скорости.
Решето Аткина
В 1999 году Аткин и Бернштейн предложили новый метод высеивания составных чисел, получивший название решета Аткина. Он основан на следующей теореме.
Теорема. Пусть n — натуральное число, которое не делится ни на какой полный квадрат. Тогда
- если n представимо в виде 4k+1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 4x2+y2 = n нечетно.
- если n представимо в виде 6k+1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 3x2+y2 = n нечетно.
- если n представимо в виде 12k-1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 3x2−y2 = n, для которых x > y, нечетно.
Из элементарной теории чисел следует, что все простые, большие 3, имеют вид 12k+1 (случай 1), 12k+5 (снова 1), 12k+7 (случай 2) или 12k+11 (случай 3).
Для инициализации алгоритма заполним решето S нулями. Теперь для каждой пары (x, y), где
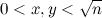 , инкрементируем значения в ячейках S[4x2+y2], S[3x2+y2], а также, если x > y, то и в S[3x2−y2]. В конце вычислений номера ячеек вида 6k±1, содержащие нечетные числа, — это или простые, или делятся на квадраты простых.
, инкрементируем значения в ячейках S[4x2+y2], S[3x2+y2], а также, если x > y, то и в S[3x2−y2]. В конце вычислений номера ячеек вида 6k±1, содержащие нечетные числа, — это или простые, или делятся на квадраты простых. В качестве заключительного этапа пройдемся по предположительно простым номерам последовательно и вычеркнем кратные их квадратам.
Из описания видно, что сложность решета Аткина пропорциональна n, а не n log log n как у алгоритма Эратосфена.
Авторская, оптимизированная реализация на Си представлена в виде primegen, упрощенная версия — в Википедии. На Хабрахабре публиковалось решето Аткина на C#.
Как и в решете Эратосфена, при помощи wheel factorization и сегментации, можно снизить асимптотическую сложность в log log n раз, а потребление памяти — до O(n½+o(1)).
О логарифме логарифма
На самом деле множитель log log n растет крайне. медленно. Например, log log 1010000 ≈ 10. Поэтому с практической точки зрения его можно полагать константой, а сложность алгоритма Эратосфена — линейной. Если только поиск простых не является ключевой функцией в вашем проекте, можно использовать базовый вариант решета Эратосфена (разве что сэкономьте на четных числах) и не комплексовать по этому поводу. Однако при поиске простых на больших интервалах (от 232) игра стоит свеч, оптимизации и решето Аткина могут ощутимо повысить производительность.
P. S. В комментариях напомнили про решето Сундарама. К сожалению, оно является лишь математической диковинкой и всегда уступает либо решетам Эратосфена и Аткина, либо проверке перебором делителей.
Литература
[1] Agrawal M., Kayal N., Saxena N. PRIMES is in P. — Annals of Math. 160 (2), 2004. — P. 781–793.
[2] Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М., МЦНМО, 2003. — 328 с.
[3] O'Neill M. E. The Genuine Sieve of Eratosthenes. — 2008.
[4] Atkin A. O. L., Bernstein D. J. Prime sieves using binary quadratic forms. — Math. Comp. 73 (246), 2003. — P. 1023-1030.