Нечеткая логика — математические основы
Нечёткое множество
Описание метода
Пусть имеется множество элементов U, а A – его нечеткое подмножество, степень принадлежности его элементов определяется значением X, принимающим значение из интервала [0;1].
Таким образом, объект можно описать набором критериев(параметров) X(1), X(2) … X(n), принадлежащих соответствующим базовым множествам U(1), U(2) … U(n). Совокупность критериев с соответствующими значениями характеризует приемлимость S данного объекта относительно поставленной задачи.
Пример такого высказывания:
d(i): «Если X(1)=низкая и X(2)=хорошее, то S=высокая»
для общего случая:
d(i): «Если X(1)=A(1) и X(2)=A(2) и… и X(p)=A(p), то S=B(i)»
Обозначим пересечение условий X(1)=A(1), X(2)=A(2) … X(n)=A(n) через X=A(i).
Пересечение нечетких множеств есть минимум их функций принадлежности:

где
V=U(1)xU(2)x...xU(p)
v=(u(1),u(2)...u(p))
u(j) — значение принадлежности элемента u(j) нечеткому множеству A(i,j)
тогда высказывание можно записать в виде:
d(i): «Если X=A(i), то S=B(i)»
Обозначим множество U или V через W, тогда A(i) – нечеткое подмножество W, а B(i) – нечеткое подмножества единичного интервала I.
Импликация этих нечетких множеств выражается как
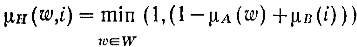
где
H- нечеткое подмножество на WxI
w принадлежит W, а i – I.
Аналогично высказывания d(1),d(2)...d(n) преобразуются в множества H(1),H(2)...H(n); их объединением является множество D.
Для каждой пары (w,i) из WxI
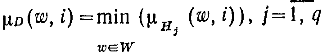
Каждая альтернатива описывается нечетким подмножеством C из W; ее удовлетворительность находится на основе компзиционного правила вывода:
G=C*D
где G – нечеткое множество интервала I. Тогда
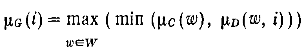
Сравнение альтернатив происходит с помошью точечных оценок.
Для нечеткого множества A из I определим a-уровневое множество (a=[0,1]):
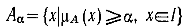
Для каждого А(а) вычисляется среднее число элементов — М(A(a)):

Тогда точечное значение для множества А:

a_max – значение, при котором A имеет максимум.
Лучшей признается альтернатива с наибольшей точечной оценкой.
Во второй части статьи будет описана реализация данного метода; пример его работы — в третьей.
Многокритериальный выбор альтернатив с использованием правил нечеткого вывода. Реализация на Java. Часть 2/3: Основной алгоритм
Многокритериальный выбор альтернатив с использованием правил нечеткого вывода. Реализация на Java. Часть 3/3: Пример
Литература:
Борисов, Крумберг, Федоров — «Принятие решений на основе нечетких моделей. Примеры использования», 1990 (прим.: в авторских расчетах имеются ошибки). Стр. 94-102
Нечёткое множество
Описание метода
Пусть имеется множество элементов U, а A – его нечеткое подмножество, степень принадлежности его элементов определяется значением X, принимающим значение из интервала [0;1].
Таким образом, объект можно описать набором критериев(параметров) X(1), X(2) … X(n), принадлежащих соответствующим базовым множествам U(1), U(2) … U(n). Совокупность критериев с соответствующими значениями характеризует приемлимость S данного объекта относительно поставленной задачи.
Пример такого высказывания:
d(i): «Если X(1)=низкая и X(2)=хорошее, то S=высокая»
для общего случая:
d(i): «Если X(1)=A(1) и X(2)=A(2) и… и X(p)=A(p), то S=B(i)»
Обозначим пересечение условий X(1)=A(1), X(2)=A(2) … X(n)=A(n) через X=A(i).
Пересечение нечетких множеств есть минимум их функций принадлежности:
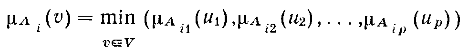
где
V=U(1)xU(2)x...xU(p)
v=(u(1),u(2)...u(p))
u(j) — значение принадлежности элемента u(j) нечеткому множеству A(i,j)
тогда высказывание можно записать в виде:
d(i): «Если X=A(i), то S=B(i)»
Обозначим множество U или V через W, тогда A(i) – нечеткое подмножество W, а B(i) – нечеткое подмножества единичного интервала I.
Импликация этих нечетких множеств выражается как
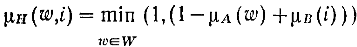
где
H- нечеткое подмножество на WxI
w принадлежит W, а i – I.
Аналогично высказывания d(1),d(2)...d(n) преобразуются в множества H(1),H(2)...H(n); их объединением является множество D.
Для каждой пары (w,i) из WxI
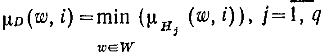
Каждая альтернатива описывается нечетким подмножеством C из W; ее удовлетворительность находится на основе компзиционного правила вывода:
G=C*D
где G – нечеткое множество интервала I. Тогда
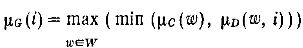
Сравнение альтернатив происходит с помошью точечных оценок.
Для нечеткого множества A из I определим a-уровневое множество (a=[0,1]):
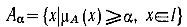
Для каждого А(а) вычисляется среднее число элементов — М(A(a)):
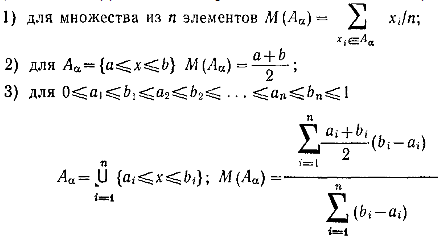
Тогда точечное значение для множества А:
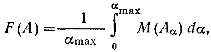
a_max – значение, при котором A имеет максимум.
Лучшей признается альтернатива с наибольшей точечной оценкой.
Во второй части статьи будет описана реализация данного метода; пример его работы — в третьей.
Многокритериальный выбор альтернатив с использованием правил нечеткого вывода. Реализация на Java. Часть 2/3: Основной алгоритм
Многокритериальный выбор альтернатив с использованием правил нечеткого вывода. Реализация на Java. Часть 3/3: Пример
Литература:
Борисов, Крумберг, Федоров — «Принятие решений на основе нечетких моделей. Примеры использования», 1990 (прим.: в авторских расчетах имеются ошибки). Стр. 94-102