Недавно я наткнулся на интересную статью, опубликованную rgen3, в которой описан DTW-алгоритм распознавания речи. В общих чертах, это сравнение речевых последовательностей с применением динамического программирования.
Заинтересовавшись темой, я попробовал применить этот алгоритм на практике, но на этом пути меня поджидало некоторое количество граблей. Прежде всего, что именно нужно сравнивать? Непосредственно звуковые сигналы во временной области — долго и не очень эффективно. Спектрограммы — уже быстрее, но не намного эффективнее. Поиски наиболее рационального представления привели меня к MFCC или Мел-частотным кепстральным коэффициентам, которые часто используются в качестве характеристики речевых сигналов. Здесь я попытаюсь объяснить, что они из себя представляют.
Объяснение начну с первого же слова в названии. Что такое мел? Википедия говорит нам, что мел – единица высоты звука, основанная на восприятии этого звука нашими органами слуха. Как известно, АЧХ человеческого уха даже отдаленно не напоминает прямую, и амплитуда – не совсем точная мера громкости звука. Поэтому, и ввели эмпирически подобранные единицы громкости, например, фон.

Аналогично, воспринимаемая человеческим слухом высота звука не совсем линейно зависит от его частоты.
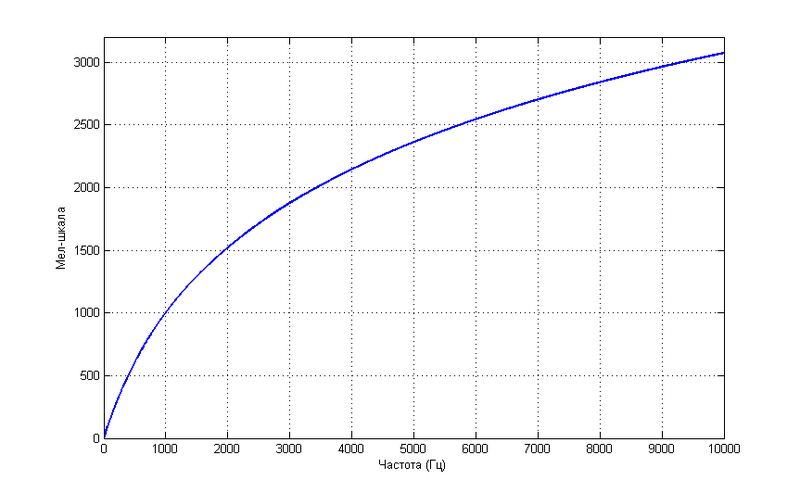
Такая зависимость не претендует на большую точность, но зато описывается простой формулой

Подобные единицы измерения часто используют при решении задач распознавания, так как они позволяют приблизиться к механизмам человеческого восприятия, которое пока что лидирует среди известных систем распознавания речи.
Нужно немного рассказать и про второе слово в названии – кепстр.
В соответствии с теорией речеобразования речь представляет собой акустическую волну, которая излучается системой органов: легкими, бронхами и трахеей, а затем преобразуется в голосовом тракте. Если предположить, что источники возбуждения и форма голосового тракта относительно независимы, речевой аппарат человека можно представить в виде совокупности генераторов тоновых сигналов и шумов, а также фильтров. Схематично это можно представить так:

1. Генератор импульсной последовательности (тонов)
2. Генератор случайных чисел (шумов)
3. Коэффициенты цифрового фильтра (параметры голосового тракта)
4. Нестационарный цифровой фильтр
Сигнал на выходе фильтра (4) можно представить в виде свертки

где s(t) — изначальный вид акустической волны, а h(t) — характеристика фильтра (зависит от параметров голосового тракта)
В частотной области это выглядит так

Произведение можно прологарифмировать, чтобы получить вместо него сумму

Теперь нам нужно преобразовать эту сумму так, чтобы получить непересекающиеся наборы характеристик исходного сигнала и фильтра. Для этого есть несколько вариантов, например обратное преобразование Фурье даст нам вот что

Также в зависимости от целей можно использовать прямое преобразование Фурье или дискретное косинусное преобразование
Надеюсь, я немного прояснил основные понятия. Осталось понять, как преобразовать речевой сигнал в набор коэффициентов MFCC.
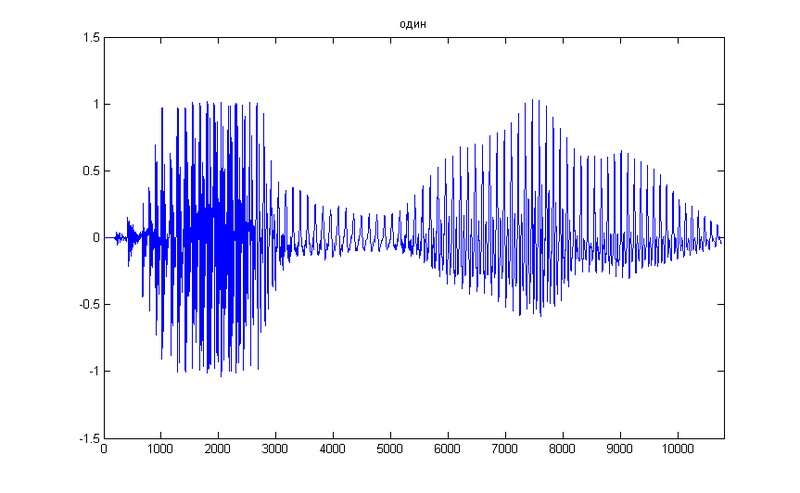
В качестве подопытной возьмем простую цифру 1, вот ее временное представление
Первым делом нам нужен спектр исходного сигнала, который мы получаем с помощью преобразования Фурье. Для простоты примера, не будем разбивать сигнал на части, поэтому берем спектр по всей временной оси

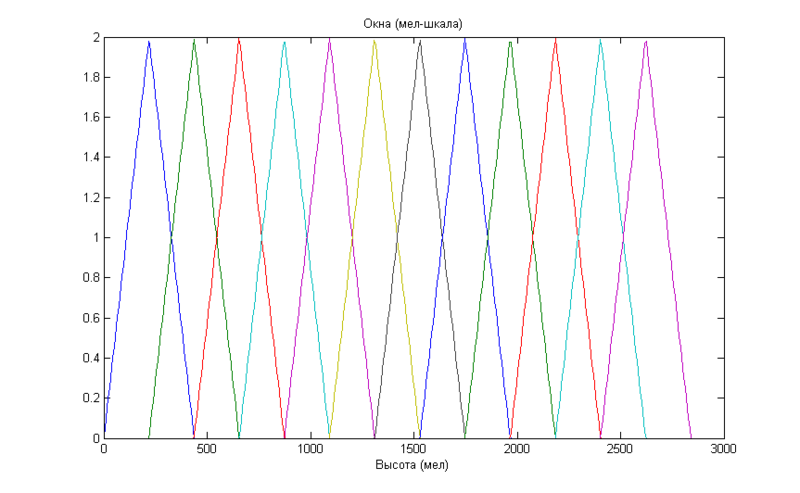
Теперь начинается самое интересное, полученный спектр нам нужно расположить на мел-шкале. Для этого мы используем окна, равномерно расположенные на мел-оси.
Если перевести этот график в частотную шкалу, можно увидеть такую картину
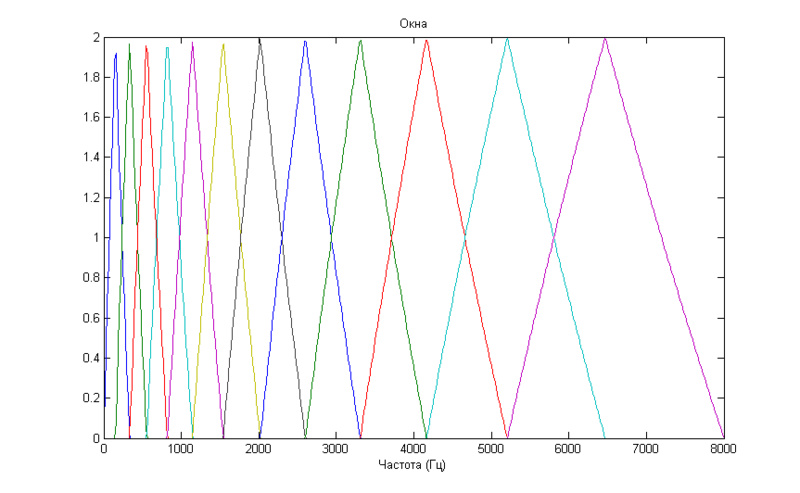
На этом графике заметно, что окна «собираются» в области низких частот, обеспечивая более высокое «разрешение» там, где оно необходимо для распознавания.
Простым перемножением векторов спектра сигнала и оконной функции найдем энергию сигнала, которая попадает в каждое из окон анализа. Мы получили некоторый набор коэффициентов, но это еще не те MFCC, которые мы ищем. Пока их можно было бы назвать Мел-частотными спектральными коэффициентами. Возводим их в квадрат и логарифмируем. Нам осталось только получить из них кепстральные, или «спектр спектра». Для этого мы могли бы еще раз применить преобразование Фурье, но лучше использовать дискретное косинусное преобразование.
В результате получаем последовательность примерно такого вида:

Таким образом мы имеем очень небольшой набор значений, который при распознавании успешно заменяет тысячи отсчетов речевого сигнала. В книгах пишут, что для задачи распознавания слов возможно брать первые 13 из 24 вычисленных коэффициентов, но сколько-нибудь годные результаты в моем случае начинались с 16. В любом случае это намного меньший объем данных, чем спектрограмма или временное представление сигнала.
Для лучшего результата можно разбить исходное слово на отрезки небольшой длительности, и вычислять коэффициенты для каждого из них. Также может помочь «взвешивание» оконных функций. Все зависит от алгоритма распознавания, которому вы скармливаете результат.
Не хочется грузить основную часть статьи большим количеством формул, но вдруг они будут кому-то интересны. Поэтому приведу их здесь.
Исходный речевой сигнал запишем в дискретном виде как
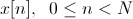
Применяем к нему преобразование Фурье
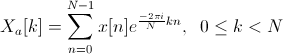
Составляем гребенку фильтров, используя оконную функцию

Для которой частоты f[m] получаем из равенства

B(b) — преобразование значения частоты в мел-шкалу, соответственно,

Вычисляем энергию для каждого окна

Применяем ДКП

Получаем набор MFCC
[1] Википедия
[2] Xuedong Huang, Alex Acero, Hsiao-Wuen Hon, Spoken Language Processing: A Guide to Theory, Algorithm, and System Development, Prentice Hall, 2001, ISBN:0130226165
Заинтересовавшись темой, я попробовал применить этот алгоритм на практике, но на этом пути меня поджидало некоторое количество граблей. Прежде всего, что именно нужно сравнивать? Непосредственно звуковые сигналы во временной области — долго и не очень эффективно. Спектрограммы — уже быстрее, но не намного эффективнее. Поиски наиболее рационального представления привели меня к MFCC или Мел-частотным кепстральным коэффициентам, которые часто используются в качестве характеристики речевых сигналов. Здесь я попытаюсь объяснить, что они из себя представляют.
Основные понятия
Объяснение начну с первого же слова в названии. Что такое мел? Википедия говорит нам, что мел – единица высоты звука, основанная на восприятии этого звука нашими органами слуха. Как известно, АЧХ человеческого уха даже отдаленно не напоминает прямую, и амплитуда – не совсем точная мера громкости звука. Поэтому, и ввели эмпирически подобранные единицы громкости, например, фон.

Аналогично, воспринимаемая человеческим слухом высота звука не совсем линейно зависит от его частоты.

Такая зависимость не претендует на большую точность, но зато описывается простой формулой

Подобные единицы измерения часто используют при решении задач распознавания, так как они позволяют приблизиться к механизмам человеческого восприятия, которое пока что лидирует среди известных систем распознавания речи.
Нужно немного рассказать и про второе слово в названии – кепстр.
В соответствии с теорией речеобразования речь представляет собой акустическую волну, которая излучается системой органов: легкими, бронхами и трахеей, а затем преобразуется в голосовом тракте. Если предположить, что источники возбуждения и форма голосового тракта относительно независимы, речевой аппарат человека можно представить в виде совокупности генераторов тоновых сигналов и шумов, а также фильтров. Схематично это можно представить так:

1. Генератор импульсной последовательности (тонов)
2. Генератор случайных чисел (шумов)
3. Коэффициенты цифрового фильтра (параметры голосового тракта)
4. Нестационарный цифровой фильтр
Сигнал на выходе фильтра (4) можно представить в виде свертки

где s(t) — изначальный вид акустической волны, а h(t) — характеристика фильтра (зависит от параметров голосового тракта)
В частотной области это выглядит так

Произведение можно прологарифмировать, чтобы получить вместо него сумму

Теперь нам нужно преобразовать эту сумму так, чтобы получить непересекающиеся наборы характеристик исходного сигнала и фильтра. Для этого есть несколько вариантов, например обратное преобразование Фурье даст нам вот что

Также в зависимости от целей можно использовать прямое преобразование Фурье или дискретное косинусное преобразование
Надеюсь, я немного прояснил основные понятия. Осталось понять, как преобразовать речевой сигнал в набор коэффициентов MFCC.
Пример
В качестве подопытной возьмем простую цифру 1, вот ее временное представление

Первым делом нам нужен спектр исходного сигнала, который мы получаем с помощью преобразования Фурье. Для простоты примера, не будем разбивать сигнал на части, поэтому берем спектр по всей временной оси

Теперь начинается самое интересное, полученный спектр нам нужно расположить на мел-шкале. Для этого мы используем окна, равномерно расположенные на мел-оси.

Если перевести этот график в частотную шкалу, можно увидеть такую картину

На этом графике заметно, что окна «собираются» в области низких частот, обеспечивая более высокое «разрешение» там, где оно необходимо для распознавания.
Простым перемножением векторов спектра сигнала и оконной функции найдем энергию сигнала, которая попадает в каждое из окон анализа. Мы получили некоторый набор коэффициентов, но это еще не те MFCC, которые мы ищем. Пока их можно было бы назвать Мел-частотными спектральными коэффициентами. Возводим их в квадрат и логарифмируем. Нам осталось только получить из них кепстральные, или «спектр спектра». Для этого мы могли бы еще раз применить преобразование Фурье, но лучше использовать дискретное косинусное преобразование.
В результате получаем последовательность примерно такого вида:

Заключение
Таким образом мы имеем очень небольшой набор значений, который при распознавании успешно заменяет тысячи отсчетов речевого сигнала. В книгах пишут, что для задачи распознавания слов возможно брать первые 13 из 24 вычисленных коэффициентов, но сколько-нибудь годные результаты в моем случае начинались с 16. В любом случае это намного меньший объем данных, чем спектрограмма или временное представление сигнала.
Для лучшего результата можно разбить исходное слово на отрезки небольшой длительности, и вычислять коэффициенты для каждого из них. Также может помочь «взвешивание» оконных функций. Все зависит от алгоритма распознавания, которому вы скармливаете результат.
Формулы
Не хочется грузить основную часть статьи большим количеством формул, но вдруг они будут кому-то интересны. Поэтому приведу их здесь.
Исходный речевой сигнал запишем в дискретном виде как
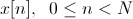
Применяем к нему преобразование Фурье
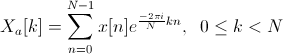
Составляем гребенку фильтров, используя оконную функцию

Для которой частоты f[m] получаем из равенства

B(b) — преобразование значения частоты в мел-шкалу, соответственно,

Вычисляем энергию для каждого окна

Применяем ДКП

Получаем набор MFCC
Источники
[1] Википедия
[2] Xuedong Huang, Alex Acero, Hsiao-Wuen Hon, Spoken Language Processing: A Guide to Theory, Algorithm, and System Development, Prentice Hall, 2001, ISBN:0130226165
