 Здравствуй, Хабр!
Здравствуй, Хабр!В этой статье речь пойдёт о небольшом программистском этюде на тему машинного обучения. Замысел его возник у меня при прохождении известного здесь многим курса «Machine Learning», читаемого Andrew Ng на Курсере. После знакомства с методами, о которых рассказывалось на лекциях, захотелось применить их к какой-нибудь реальной задаче. Долго искать тему не пришлось — в качестве предметной области просто напрашивалась оптимизация собственного шахматного движка.
Вступление: о шахматных программах
Не будем детально углубляться в архитектуру шахматных программ — это могло бы стать темой отдельной публикации или даже их серии. Рассмотрим только самые базовые принципы. Основными компонентами практически любого небелкового шахматиста являются поиск и оценка позиции.
Поиск представляет собой перебор вариантов, то есть итеративное углубление по дереву игры. Оценочная функция отображает набор позиционных признаков на числовую шкалу и служит целевой функцией для поиска наилучшего хода. Она применяется к листьям дерева, и постепенно «возвращается» к исходной позиции (корню) с помощью альфа-бета процедуры или её вариаций.
Строго говоря, настоящая оценка может принимать только три значения: выигрыш, проигрыш или ничья — 1, 0 или ½. По теореме Цермело для любой заданной позиции она определяется однозначно. На практике же из-за комбинаторного взрыва ни один компьютер не в состоянии просчитать варианты до листьев полного дерева игры (исчерпывающий анализ в эндшпильных базах данных — это отдельный случай; 32-фигурных таблиц в обозримом будущем не появится… и в необозримом, скорее всего, тоже). Поэтому программы работают в так называемой модели Шеннона — пользуются усечённым деревом игры и приближённой оценкой, основанной на различных эвристиках.
Поиск и оценка не существуют независимо друг от друга, они должны быть хорошо сбалансированы. Современные переборные алгоритмы давно уже не являются «тупым» перебором вариантов, они включают в себя многочисленные специальные правила, связанные в том числе и с оценкой позиции.
Первые такие усовершенствования поиска появились ещё на заре шахматного программирования, в 60-х годах XX в. Можно упомянуть, например, технику форсированного варианта (ФВ) — продление отдельных ветвей поиска до тех пор, пока позиция не «успокоится» (закончатся шахи и взаимные взятия фигур). Продления существенно увеличивают тактическую зоркость компьютера, а также приводят к тому, что дерево поиска становится очень неоднородным — длина отдельных ветвей может в несколько раз превышать длину соседних, менее перпективных. Другие улучшения поиска, наоборот, представляют собой отсечения или сокращения поиска — и здесь критерием отбрасывания плохих вариантов может, в числе прочего, служить всё та же статическая оценка.
Параметризация и улучшение поиска методами машинного обучения — отдельная интересная тема, но сейчас мы оставим её в стороне. Займёмся пока только оценочной функцией.
Как компьютер оценивает позицию
 Статическая оценка представляет собой линейную комбинацию различных признаков позиции, взятых с некоторыми весовыми коэффициентами. Какие это признаки? В первую очередь, количество фигур и пешек у той и другой стороны. Следующий важный признак — положение этих фигур, централизация, занятие дальнобойными фигурами открытых линий и диагоналей. Опыт показывает, что учёт только этих двух факторов — суммы материала и относительной ценности полей (зафиксированной в виде таблиц для каждого типа фигур) — при наличии качественного поиска уже может обеспечивать силу игры в диапазоне до 2000-2200 пунктов Эло. Это уровень хорошего первого разряда или кандидата в мастера.
Статическая оценка представляет собой линейную комбинацию различных признаков позиции, взятых с некоторыми весовыми коэффициентами. Какие это признаки? В первую очередь, количество фигур и пешек у той и другой стороны. Следующий важный признак — положение этих фигур, централизация, занятие дальнобойными фигурами открытых линий и диагоналей. Опыт показывает, что учёт только этих двух факторов — суммы материала и относительной ценности полей (зафиксированной в виде таблиц для каждого типа фигур) — при наличии качественного поиска уже может обеспечивать силу игры в диапазоне до 2000-2200 пунктов Эло. Это уровень хорошего первого разряда или кандидата в мастера.Дальнейшее уточнение оценки может включать всё более и более тонкие признаки шахматной позиции: наличие и продвинутость проходных пешек, близость фигур к позиции неприятельского короля, его пешечное прикрытие и т. д. Легендарная «Каисса», первая чемпионка мира среди программ (1974) имела оценочную функцию из нескольких десятков признаков. Все они подробно описаны в книге «Машина играет в шахматы», библиографическая ссылка на которую приводится в конце статьи.

Одна из самых «навороченных» оценочных функций была у машины Deep Blue, прославившейся своими матчами с Каспаровым в 1996-97 гг. (подробную историю этих матчей можно прочитать в недавней серии статей на Geektimes.)
Широко распространено мнение, что сила Deep Blue основывалась исключительно на колоссальной скорости перебора вариантов. 200 миллионов позиций в секунду, полный (без отсечений) перебор на 12 полуходов — к таким параметрам шахматные программы на современном железе только-только приближаются. Однако, дело было не только в быстродействии. По объёму «шахматных знаний» в оценочной функции эта машина также намного превосходила всех. Оценка Deep Blue была реализована аппаратно и включала до 8000 различных признаков. Для настройки её коэффициентов привлекались сильные гроссмейстеры (достоверно известно о работе с Джоэлем Бенджамином, тестовые партии с разными версиями машины играл Давид Бронштейн).
Не располагая такими ресурсами, как создатели Deep Blue, ограничим задачу. Из всех признаков позиции, учитываемых для подсчёта оценки, возьмём самый значимый — соотношение материала на доске.
Стоимость фигур: простейшие модели
Если взять любую шахматную книгу для начинающих, сразу за главой с объяснением шахматных ходов обычно приводится табличка сравнительной ценности фигур, примерно такая:
| Тип | Стоимость |
|---|---|
| Пешка | 1 |
| Конь | 3 |
| Слон | 3 |
| Ладья | 5 |
| Ферзь | 9 |
| Король | ∞ |
Приведённые стоимости фигур должны рассматриваться только как некоторые базовые ориентиры. В реальности фигуры могут «дорожать» и «дешеветь» в зависимости от ситуации на доске, а также от стадии партии. В качестве поправки первого порядка обычно рассматривают комбинации из двух-трёх фигур — своих и противника.
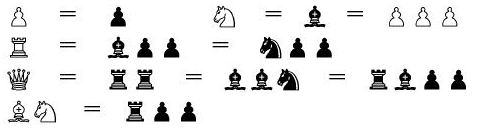
Вот как оценивал различные сочетания материала в своём классическом «Учебнике шахматной игры» третий чемпион мира Хосе-Рауль Капабланка:
С точки зрения общей теории слона и коня следует считать одинаково ценными, хотя, по моему убеждению, слон в большинстве случаев оказывается более сильной фигурой. Между тем считается вполне установленным, что два слона почти всегда сильнее двух коней.
Слон в игре против пешек сильнее коня, а вместе с пешками также оказывается более сильным против ладьи, нежели конь. Слон и ладья тоже сильнее коня и ладьи, но ферзь и конь могут оказаться сильнее, чем ферзь и слон. Слон часто стоит больше трех пешек, о коне же это редко можно сказать; он даже может оказаться слабее трех пешек.
Ладья по силе равна коню и двум пешкам или же слону и двум пешкам, но, как сказано выше, слон в борьбе против ладьи сильнее коня. Две ладьи несколько сильнее ферзя. Они немного слабее двух коней и слона и еще слабее двух слонов и коня. Сила коней падает по мере размена фигур на доске, сила же ладьи, напротив, возрастает.
Наконец, как правило, три легкие фигуры сильнее ферзя.
Оказывается, большей части подобных правил можно удовлетворить, оставаясь в рамках линейной модели, и просто слегка сместив стоимости фигур от их «школьных» значений. Например, в одной из статей приводятся следующие граничные условия:
B > N > 3P
B + N = R + 1.5P
Q + P = 2RИ значения, им удовлетворяющие:
P = 100
N = 320
B = 330
R = 500
Q = 900
K = 20000
Имена переменных соответствуют обозначениям фигур в английской нотации: P — пешка, N — конь, B — слон, R — ладья, Q — ферзь, K — король. Стоимости здесь и далее указаны в сотых долях пешки.
На самом деле, приведённый набор значений не является единственным решением. Более того, даже несоблюдение каких-то из «неравенств им. Капабланки» не приведёт к резкому падению силы игры программы, а только повлияет на её стилевые особенности.
В качестве эксперимента я провёл небольшой матч-турнир четырёх версий своего движка GreKo с разными весами фигур против трёх других программ — каждая из версий сыграла 3 матча по 200 партий со сверхмалым контролем времени (1 секунда + 0.1 сек. на ход). Результаты приведены в таблице:
| Версия | Пешка | Конь | Слон | Ладья | Ферзь | vs. Fruit 2.1 | vs. Crafty 23.4 | vs. Delfi 5.4 | Рейтинг |
|---|---|---|---|---|---|---|---|---|---|
| GreKo 12.5 | 100 | 400 | 400 | 600 | 1200 | 61.0 | 76.0 | 71.0 | 2567 |
| GreKo A | 100 | 300 | 300 | 500 | 900 | 55.0 | 69.0 | 73.0 | 2552 |
| GreKo B | 100 | 320 | 330 | 500 | 900 | 57.0 | 71.0 | 64.0 | 2548 |
| GreKo C | 100 | 325 | 325 | 550 | 1100 | 72.5 | 74.5 | 69.0 | 2575 |
«Классические» стоимости шахматного материала были получены интуитивно, путём осмысления шахматистами своего практического опыта. Предпринимались также попытки подвести под эти значения какую-то математическую базу — например, на основе мобильности фигур, числа полей, которые они могут держать под контролем. Мы же попробуем подойти к вопросу экспериментально — на базе анализа большого количества шахматных партий. Для вычисления стоимостей фигур нам не понадобится приближённая оценка позиций из этих партий — только их результаты, как самая объективная мера успеха в шахматах.
Материальный перевес и логистическая кривая
Для статистического анализа был взят PGN-файл, содержащий почти 3000 шахматных партий в блиц между 32 разными шахматными движками, в диапазоне от 1800 до 3000 пунктов Эло. С помощью специально написанной утилиты для каждой партии был составлен список материальных соотношений, возникших на доске. Каждое соотношение материала попадало в статистику не сразу после взятия фигуры или превращения пешки — сначала должны были произойти ответные взятия или несколько «тихих» ходов. Таким образом отфильтровывались краткосрочные «скачки материала» на 1-2 хода при разменах.
Затем по уже известной нам шкале «1-3-3-5-9» рассчитывался материальный баланс позиции, и для каждого его значения (от -24 до 24) накапливалось количество очков, набранных белыми. Полученная статистика представлена на следующем графике:

По оси x — материальный баланс позиции ΔM с точки зрения белых, в пешках. Он вычисляется как разность суммарной стоимости всех белых фигур и пешек и такой же величины для чёрных. По оси y — выборочное математическое ожидание результата партии (0 — победа чёрных, 0.5 — ничья, 1 — победа белых). Мы видим, что экспериментальные данные очень хорошо описываются логистической кривой:

Простой визуальный подбор позволяет определить параметр кривой: α=0.7, размерность его — обратные пешки.
Для сравнения на графике приведены ещё две логистические кривые с другими значениями параметра α.
Что это означает на практике? Пусть мы видим случайно выбранную позицию, в которой у белых перевес в 2 пешки (ΔM = 2). С вероятностью, близкой к 80%, мы можем утверждать: партия закончится победой белых. Аналогично, если у белых не хватает слона или коня (ΔM = -3), их шансы не проиграть всего лишь около 12%. Позиции с материальным равенством (ΔM = 0), как и можно было ожидать, чаще всего заканчиваются вничью.
Постановка задачи
Теперь мы готовы сформулировать задачу оптимизации оценочной функции в терминах логистической регрессии.
Пусть нам дан набор векторов следующего вида:

где Δi, i = P...Q — разность количества белых и чёрных фигур типа i (от пешки до ферзя, короля не считаем). Эти вектора представляют собой материальные соотношения, встретившиеся в партиях (одной партии обычно соответствует несколько векторов).
Пусть дан также вектор yj, компоненты которого принимают значения 0, 1 и 2. Эти значения соответствуют исходам партий: 0 — победа чёрных, 1 — ничья, 2 — победа белых.
Требуется найти вектор θ стоимостей фигур:

минимизирующий функцию стоимости для логистической регрессии:
![J(\theta)=\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] J(\theta)=\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))]](https://habrastorage.org/getpro/habr/post_images/173/1cc/a03/1731cca030c122aef66c4d2ee08fc495.png) ,
,где
 — логистическая функция для векторного аргумента.
— логистическая функция для векторного аргумента.Для предотвращения «переобучения» и эффектов неустойчивости в найденном решении в функцию стоимости можно добавить параметр регуляризации, не дающий коэффициентам в векторе принимать слишком большие значения:

Величина коэффициента при параметре регуляризации выбирается небольшая, в данном случае использовалось значение λ=10-6.
Для решения задачи минимизации применим простейший метод градиентного спуска с постоянным шагом:

где компоненты градиента функции Jreg имеют вид:


Так как мы ищем симметричное решение, при материальном равенстве дающее вероятность исхода партии ½, нулевой коэффициент вектора θ полагаем всегда равным нулю, и нам для градиента нужно только второе из данных выражений.
Вывод приведённых формул мы здесь рассматривать не будем. Всем интересующимся их обоснованием настоятельно рекомендую уже упоминавшийся курс по машинному обучению на Coursera.
Программа и результаты
Так как первая часть задачи — разбор PGN-файлов и выделение для каждой позиции набора признаков — уже была практически реализована в коде шахматного движка, оставшуюся часть было решено также написать на C++. Исходный код программы и тестовые наборы партий в PGN-файлах доступны на github. Программа может быть собрана и запущена под Windows (MSVC) или Linux (gcc).
Возможность использовать в дальнейшем специализированные средства вроде Octave, MATLAB, R и т.п. также предусмотрена — в процессе работы программа генерирует промежуточный текстовый файл с наборами признаков и исходами партий, который легко может быть импортирован в эти среды.
Файл содержит текстовое представление набора векторов xj — матрицы размерности m x (n + 1), в первых 5 столбцах которой содержатся компоненты материального баланса (от пешки до ферзя), а в 6-м — результат партии.
Рассмотрим простой пример. Ниже приводится PGN-запись одной из тестовых партий.
[Event "OpenRating 31"]
[Site "BEAR-HOME"]
[Date "2013.05.09"]
[Round "1"]
[White "Simplex 0.9.7"]
[Black "IvanHoe 999946f"]
[Result "0-1"]
[TimeControl "60+1"]
[PlyCount "96"]
1. d4 d5 2. c4 e6 3. e3 c6 4. Nf3 Nd7 5. Nbd2 Nh6 6. e4 Bb4 7. a3 Ba5 8.
cxd5 exd5 9. exd5 cxd5 10. Qe2+ Kf8 11. Qb5 Nf6 12. Bd3 Qe7+ 13. Kd1 Bb6
14. Re1 Bd7 15. Qb3 Be6 16. Re2 Qc7 17. Qb4+ Kg8 18. Nb3 Bf5 19. Bb1 Bxb1
20. Rxb1 Nf5 21. Bd2 a5 22. Qa4 h6 23. Rc1 Qb8 24. Bxa5 Qf4 25. Qb4 Bxa5
26. Nxa5 Kh7 27. Nxb7 Rab8 28. a4 Ne4 29. h3 Rhc8 30. Ra1 Rc7 31. Qa3 Rcxb7
32. g3 Qc7 33. Rc1 Qa5 34. Rxe4 dxe4 35. Rc5 Qa6 36. Nd2 Nxd4 37. Rc4 Nb3
38. Nxb3 Qxc4 39. Nd2 Rd8 40. Qc3 Qf1+ 41. Kc2 Qe2 42. f4 e3 43. b4 Rc7 44.
Kb3 Qd1+ 45. Ka2 Rxc3 46. Nb1 Qxa4+ 47. Na3 Rc2+ 48. Ka1 Rd1# 0-1Соответствующий фрагмент промежуточного файла имеет вид:
0 0 0 0 0 0
1 0 0 0 0 0
2 0 0 0 0 0
2 -1 0 0 0 0
2 0 0 -1 0 0
1 0 0 -1 0 0
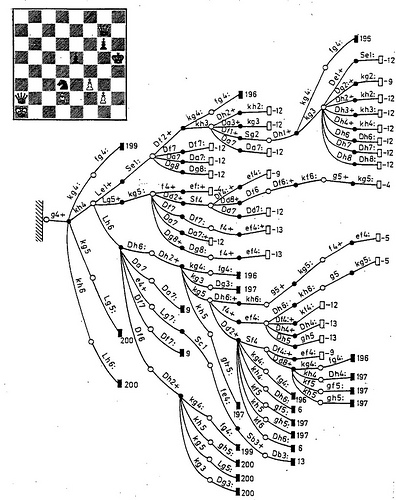
1 1 0 -2 0 0В 6-м столбце везде 0 — это результат партии, победа чёрных. В остальных столбцах — баланс числа фигур на доске. В первой строке полное материальное равенство, все компоненты равны 0. Вторая строка — лишняя пешка у белых, это позиция после 24-го хода. Обратим внимание, что предшествующие размены никак не отражены, они происходили слишком быстро. После 27-го хода у белых уже 2 лишних пешки — это строка 3. И т.д. Перед заключительной атакой чёрных у белых пешка и конь за две ладьи:
Как и размены в дебюте, финальные ходы в партии на содержимое файла не повлияли. Они были отсеяны «фильтром тактики», потому что представляли собой серию взятий, шахов и уходов от них.
Такие же записи создаются для всех анализируемых партий, в среднем получается по 5-10 строк на игру. После разбора PGN-базы с партиями этот файл поступает на вход второй части программы, занимающейся собственно решением задачи минимизации.
В качестве начальной точки для градиентного спуска можно, например, взять вектор со значениями весов фигур из учебника. Но интереснее не давать алгоритму никаких подсказок, и стартовать из нуля. Оказывается, наша функция стоимости достаточно «хорошая» — траектория быстро, за несколько тысяч шагов, выходит на глобальный минимум. Как изменяются при этом стоимости фигур, показано на следующем графике (на каждом шаге выполнялась нормировка на вес пешки = 100):

График сходимости функции стоимости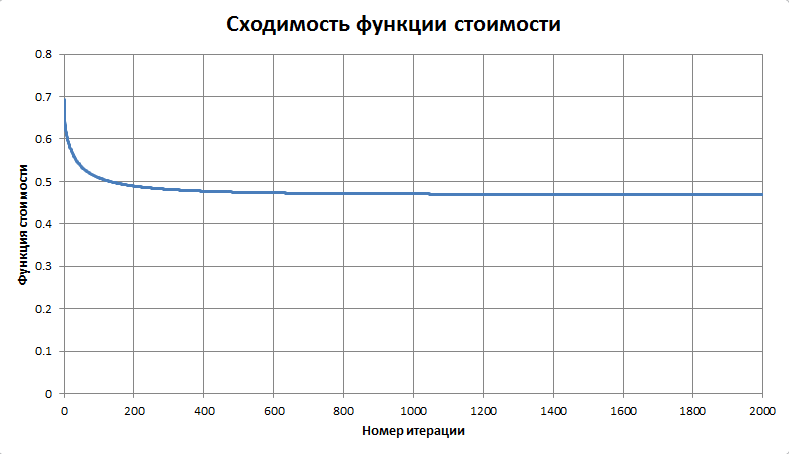

Текстовый вывод программы
C:\CHESS>pgnlearn.exe OpenRating.pgn
Reading file: OpenRating.pgn
Games: 2997
Created file: OpenRating.mat
Loading dataset...
[ 20196 x 5 ]
Solving (gradient method)...
Iter 0: [ 0 0 0 0 0 ] -> 0.693147
Iter 1000: [ 0.703733 1.89849 2.31532 3.16993 6.9148 ] -> 0.470379
Iter 2000: [ 0.735853 2.08733 2.51039 3.47418 7.7387 ] -> 0.469398
Iter 3000: [ 0.74429 2.13676 2.56152 3.55386 7.95879 ] -> 0.46933
Iter 4000: [ 0.746738 2.15108 2.57635 3.57697 8.02296 ] -> 0.469324
Iter 5000: [ 0.747467 2.15535 2.58077 3.58385 8.0421 ] -> 0.469324
Iter 6000: [ 0.747685 2.15663 2.58209 3.58591 8.04785 ] -> 0.469324
Iter 7000: [ 0.747751 2.15702 2.58249 3.58653 8.04958 ] -> 0.469324
Iter 8000: [ 0.747771 2.15713 2.58261 3.58672 8.0501 ] -> 0.469324
Iter 9000: [ 0.747777 2.15717 2.58265 3.58678 8.05026 ] -> 0.469324
Iter 10000: [ 0.747779 2.15718 2.58266 3.58679 8.0503 ] -> 0.469324
PIECE VALUES:
Pawn: 100
Knight: 288.478
Bishop: 345.377
Rook: 479.66
Queen: 1076.56
Press ENTER to finishПосле нормировки и округления получаем следующий набор величин:
| Тип | Стоимость |
|---|---|
| Пешка | 100 |
| Конь | 288 |
| Слон | 345 |
| Ладья | 480 |
| Ферзь | 1077 |
| Король | ∞ |
| Соотношение | Численные значения | Выполняется? |
|---|---|---|
| B > N | 345 > 288 | да |
| B > 3P | 345 > 3 * 100 | да |
| N > 3P | 288 < 3 * 100 | нет |
| B + N = R + 1.5P | 345 + 288 ~= 480 + 1.5 * 100 | да (с погрешностью < 0.5%) |
| Q + P = 2R | 1077 + 100 > 2 * 480 | нет |
Можно ли полученные значения использовать для усиления игры программы? Увы, на данном этапе ответ отрицательный. Тестовые блиц-матчи показывают, что сила игры GreKo от использования найденных параметров практически не изменилась, а в ряде случаев даже снизилась. Почему так произошло? Одна из очевидных причин — уже упоминавшаяся тесная связь поиска и оценки позиции. В поиске движка заложен целый ряд эвристик для отсечения неперспективных ветвей, и критерии этих отсечений (пороговые значения) тесно завязаны на статическую оценку. Меняя стоимости фигур, мы резко сдвигаем масштаб величин — форма дерева поиска меняется, требуется новая балансировка констант для всех эвристик. Это достаточно трудоёмкая задача.
Эксперимент с партиями людей
Попробуем расширить наш эксперимент, рассмотрев игры не только компьютеров, но и людей. В качестве массива данных для обучения возьмём партии двух выдающихся современных гроссмейстеров — чемпиона мира Магнуса Карлсена и экс-чемпиона Ананда Вишванатана, а также представителя романтических шахмат XIX столетия Адольфа Андерсена.

Ананд и Карлсен соперничают за мировую корону
В таблице ниже представлены результаты решения регрессионной задачи для партий этих шахматистов.
| Ананд | Карлсен | Андерсен | |
|---|---|---|---|
| Пешка | 100 | 100 | 100 |
| Конь | 216 | 213 | 286 |
| Слон | 230 | 243 | 289 |
| Ладья | 355 | 352 | 531 |
| Ферзь | 762 | 786 | 1013 |
| Король | ∞ | ∞ | ∞ |
Надо сказать, что похожая картина наблюдается не только у Виши и Магнуса, но и для большинства гроссмейстеров, партии которых удалось протестировать. Причём какой-то зависимости от стиля не выяснилось. Значения смещены от классических в одну и ту же сторону и у позиционных мастеров вроде Михаила Ботвинника и Анатолия Карпова, и у атакующих шахматистов — Михаила Таля, Юдит Полгар…
Одним из немногих исключений стал Адольф Андерсен — лучший европейский игрок середины XIX века, автор знаменитой «вечнозелёной партии». Вот для него значения стоимости фигур оказались очень близки к тем, которые используют компьютерные программы. Напрашиваются самые разнообразные фантастические гипотезы, вроде тайного читерства немецкого маэстро через портал во времени… (Шутка, конечно. Адольф Андерсен был крайне порядочным человеком, и никогда бы себе такого не позволил.)

Адольф Андерсен (1818-1879),
человек-компьютер
Почему наблюдается такой эффект со сжатием диапазона стоимости фигур? Конечно, не стоит забывать о крайней ограниченности нашей модели — учёт дополнительных позиционных факторов мог бы внести существенные коррективы. Но, возможно, дело в слабой технике реализации человеком материального перевеса — относительно современных шахматных программ, конечно. Проще говоря, человеку тяжело безошибочно играть ферзём, потому что у того слишком много возможностей. Вспоминается хрестоматийный анекдот о Ласкере (в других вариантах — Капабланке / Алехине / Тале), якобы игравшем с форой со случайным попутчиком в поезде. Кульминационной фразой было: «Ферзь только мешает!»
Заключение
Мы рассмотрели один из аспектов оценочной функции шахматных программ — стоимость материала. Убедились, что эта часть статической оценки в модели Шеннона имеет вполне «физический» смысл — она гладким образом (через логистическую функцию) связана с вероятностью исхода партии. Затем рассмотрели несколько распространённых комбинаций весов фигур, и оценили порядок их влияния на силу игры программы.
С помощью аппарата регрессии на партиях различных шахматистов, как живых так и компьютерных, мы определили оптимальные стоимости фигур в предположении чисто материальной оценочной функции. Обнаружили интересный эффект меньшей стоимости материала для людей по сравнению с машинами, и «заподозрили в читерстве» одного из шахматных классиков. Попробовали применить найденные значения в реальном движке и… не добились особого успеха.
Куда двигаться дальше? Для более точной оценки позиции можно добавлять в модель новые шахматные знания — то есть увеличивать размерность векторов x и θ. Даже оставаясь в области только материальных критериев (без учёта полей, занимаемых фигурами на доске), можно добавить целый ряд релевантных признаков: два слона, пара из ферзя и коня, пара из ладьи и слона, разноцвет, последняя пешка в эндшпиле… Шахматистам хорошо известно, как ценность фигур может зависеть от их сочетания или стадии партии. В шахматных программах соответствующие веса (бонусы или штрафы) могут достигать десятых долей пешки и более.
Один из возможных путей (наряду с увеличением размера выборки) — использовать для обучения партии, сыгранные предыдущей версией той же самой программы. В таком случае есть надежда на бóльшую согласованность одних признаков оценки с другими. Можно также в качестве функции стоимости использовать не успех предсказания исхода партии (которая может закончиться через несколько десятков ходов после рассматриваемой позиции), а корреляцию статической оценки с динамической — т.е. с результатом альфа-бета поиска на определённую глубину.
Однако, как уже было отмечено выше, для непосредственного усиления игры программы полученные результаты могут оказаться непригодными. Часто случается так: после обучения на сериях тестов программа начинает лучше решать тесты (в нашем случае — предсказывать результаты партий), но не лучше играть! В настоящее время в шахматном программировании мейнстримом стало интенсивное тестирование исключительно в практической игре. Новые версии топ-движков перед выпуском тестируются на десятках и сотнях тысяч партий со сверхкороткими контролями времени…
В любом случае, я планирую провести ещё ряд экспериментов по статистическому анализу шахматных партий. Если данная тема представляет интерес для аудитории Хабра, при получении каких-либо нетривиальных результатов статья может получить продолжение.
В ходе исследований ни одна шахматная фигура не пострадала.

Библиография
Адельсон-Вельский, Г.М.; Арлазаров, В.Л.; Битман, А.Р. и др. — Машина играет в шахматы. М.: Наука, 1983
Книга авторов советской программы «Каисса», подробно описывающая как общие алгоритмические основы шахматных программ, так и конкретные детали реализации оценочной функции и поиска «Каиссы».
Корнилов Е. — Программирование шахмат и других логических игр. СПб.: БХВ-Петербург, 2005
Более современная и «практическая» книга, содержит большое количество примеров кода.
Feng-hsiung Hsu — Behind Deep Blue. Princeton University Press, 2002
Книга одного из создателей шахматной машины Deep Blue, в подробностях рассказывающая об истории её создания и внутреннем устройстве. В приложении приведены тексты всех шахматных партий, сыгранных Deep Blue в официальных соревнованиях.
Ссылки
Chessprogramming Wiki — обширная коллекция материалов по всем теоретическим и практическим аспектам шахматного программирования.
Machine Learning in Games — сайт, посвящённый машинному обучению в играх. Содержит большое количество научных статей по исследованиям в области шахмат, шашек, го, реверси, нардов и т.д.
Kaissa — страница, посвящённая «Каиссе». Детально представлены коэффициенты её оценочной функции.
Stockfish — сильнейшая на сегодня программа, с открытым исходным кодом.
A comparison of Rybka 1.0 beta and Fruit 2.1
Детальное сравнение внутреннего устройства двух популярных шахматных программ.
GreKo — шахматная программа автора статьи.
Была использована в качестве одного из источников тестовых компьютерных партий. Также на основе её генератора ходов и парсера PGN-нотации была изготовлена утилита для анализа экспериментальных данных.
pgnlearn — код утилиты и примеры файлов с партиями на github.
 С точки зрения общей теории слона и коня следует считать одинаково ценными, хотя, по моему убеждению, слон в большинстве случаев оказывается более сильной фигурой. Между тем считается вполне установленным, что два слона почти всегда сильнее двух коней.
С точки зрения общей теории слона и коня следует считать одинаково ценными, хотя, по моему убеждению, слон в большинстве случаев оказывается более сильной фигурой. Между тем считается вполне установленным, что два слона почти всегда сильнее двух коней.