Как я и обещал, перехожу от обзора программ замены калькулятора к более серьезным инструментам. Если помните схему из предыдущего поста, то во второй категории находились табличные: OpenOffice / LibreOffice сотоварищи. Эту партию мы можем смело пропустить, так как к командной строке она не относится, к тому же, среди читателей Хабра трудно найти человека, который бы в них не разбирался. Поэтому перехожу сразу к третьей категории.
Специализированные математические программы, уровень студент+
- GNU
Octave. Scilab.Maxima.R.Sage.
На первом месте в этом списке находится Octave, и это не случайность. Исследователи из Университета Мэриленда в США провели сравнительный анализ математических вычислений, используя MATLAB, Octave, SciLab и FreeMat в простом сценарии и в сложном. В первом случае решали систему линейных уравнений а в втором — конечно-разностную дискретизацию уравнения Пуассона в двухмерном пространстве. Основной вывод — GNU Octave справляется с задачами лучше остальных открытых математических пакетов, демонстрируя результат (страницы 23 и 25) сопоставимый с матлабовским.
Но сначала немного исторического контекста, чтобы понять, как закалялись математические программы с открытыми исходниками.
Догнать и перегнать MATLAB
Так сложилось, что коммерческие программы прибежали и первыми застолбили поляну математических вычислений. Уже с конца 1970-х гг. создатель языка программирования Клив Моулер распространяет MATLAB в университетах США, а в 1984-м вместе с двумя компаньонами переписывают его с Фортрана на Си и создают компанию The MathWorks. Примечательно, что ранние версии распространялись с открытым исходным кодом.
Это было-было, а MATLAB, каким мы его знаем сегодня — это ЯП высокого уровня с поддержкой 2D / 3D графики, разнообразными математическими функциями, интерактивной средой программирования, численных расчетов и решения задач. Внешние интерфейсы позволяют ему интегрироваться со сторонними приложениями и языками программирования. Более 1 000 000 инженеров и ученых по всему миру используют MATLAB и платят за это солидную денежку.
С большим опозданием в игру включаются программы с открытыми исходниками. Только в 1990-х появляются математические пакеты GNU Octave, Scilab и вступают в конкуренцию с лидером вычислительного программирования.
Задуманный изначально как программное пособие для проектирования химического реактора и названный в честь профессора химии Октава Левеншпиля, преподававшего автору математического пакета, Octave призван был заменить студентам Техасского Университета сложный в отладке Fortran. Версия 1.0 вышла в свет 17 февраля 1994 г. Проект стабильно развивается, и в июле нынешнего года зарелизился Octave 4.0.3. Ждем ебилдов.

Основной миссией Octave была, и в обозримом будущем скорее всего так и останется, быть годной заменой MATLAB так же, как OpenOffice/LibreOffice замещает MS Office для тех, кто умеет считать копейку. Собственно, для этого Octave имеет совместимый с MATLAB синтаксис и набор функций. Более того, несовместимость с MATLAB считается багом, однако софтверная Фемида уже имеет подобный прецедент, и это не считается нарушением копирайта. В этой связи, можно считать Octave программным клоном. Правда о полной совместимости пока говорить не приходится, но работа в этом направлении не прекращается.
Octave написан на C++, используя стандартную библиотеку шаблонов, имеет интерактивный командный интерфейс, поддерживает расширения — динамически загружаемые модули на родном языке или на C, C++, Fortran и др. Так же как и MATLAB, в алгебраических вычислениях Octave использует библиотеки Basic Linear Algebra Subroutines (BLAS) и Linear Algebra Package (LAPACK).
Установка
Установка Octave в Linux ничем не отличается от установки других программ. На Gentoo Linux запускаем:
$ sudo emerge -av octave
Дебианщики делают то же самое с помощью apt.
$ sudo aptitude install octave
Для SUSE и Arch тоже все очень просто, а вот пользователям Красной Шапки и CentOS придется чуток повозиться. Попытка установить Octave легким движением кисти завершается ошибкой, пакет в репозитариях не найден.
[root@server ~]# yum install octave Загружены модули: langpacks, product-id, subscription-manager This system is not registered to Red Hat Subscription Management. You can use subscription-manager to register. HighAvailability | 4.1 kB 00:00:00 ResilientStorage | 4.1 kB 00:00:00 server | 4.1 kB 00:00:00 vmware-tools | 951 B 00:00:00 Пакета с названием octave не найдено. Ошибка: Выполнять нечего
Благо, есть обходной путь. Нужно сперва установить пакет epel-release.
[root@server ~]# wget https://dl.fedoraproject.org/pub/epel/7/x86_64/ [root@server ~]# yum localinstall epel-release-6-7.noarch.rpm
И только после этого yum install octave сработает.
Наконец, все готово и программа установлена.
[root@server ~]# octave GNU Octave, version 3.8.2 Copyright (C) 2014 John W. Eaton and others. This is free software; see the source code for copying conditions. There is ABSOLUTELY NO WARRANTY; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. For details, type 'warranty'. Octave was configured for "x86_64-redhat-linux-gnu". Additional information about Octave is available at http://www.octave.org. Please contribute if you find this software useful. For more information, visit http://www.octave.org/get-involved.html Read http://www.octave.org/bugs.html to learn how to submit bug reports. For information about changes from previous versions, type 'news'. octave:1>
Операции с матрицами
Не будем терять время и делать операции, которые можно повторить с помощью bc и awk, о ктоторых речь шла в прошлый раз. Поиграемся немного с матрицами.
Сперва простое транспонирование матрицы:
octave:1> A=[1 3 5; 2 4 6] A = 1 3 5 2 4 6 octave:2> A' ans = 1 2 3 4 5 6
Попробуем решить систему линейных уравнений:
x + y + z = 9 2x + 4y - 3z = 1 3x + 6y - 5z = 0
Вбиваем матрицу A, вектор b и решаем уравнение Ax = b в матричном виде
octave:1> A=[1 1 1; 2 4 -3; 3 6 -5] A = 1 1 1 2 4 -3 3 6 -5 octave:2> b=[9; 1; 0] b = 9 1 0 octave:3> x=A\b x = 7.00000 -1.00000 3.00000
Находим детерминант и собственные значения матрицы.
octave:4> det (A) ans = -1.00000 octave:5> eig (A) ans = -2.88897 2.76372 0.12525
Комплексные числа тоже поддерживаются в вычислениях.
octave:6> A=[-3 0 2; 1 -1 0; -2 -1 0] A = -3 0 2 1 -1 0 -2 -1 0 octave:7> x=det (A) x = -6 octave:8> y=eig(A) y = -1.00000 + 1.41421i -1.00000 - 1.41421i -2.00000 + 0.00000i
Функции и переменные
В Octave переменные и функции создавать гораздо проще, чем, к примеру, в Java или C. На примере матриц, мы уже видели как объявлять переменные. Создания новой функции имеет следующий синтаксис
function [res1, res2, ..., resM] = имя_функции (arg1, arg2, ..., argN) тело функции endfunction
Как правило, новую функцию создают либо в отдельном файле, либо в скрипт-файле Octave
до первого ее вызова. Если предполагается использовать пользовательскую функцию в разных скрипт-файлах, то, конечно, предпочтительно создать ее в отдельном файле. В GNU Octave файлы с функциями имеют расширение .m и загружаются автоматически. Имя файла должно строго совпадать с именем функции.
Напишем функцию для решения квадратичного уравнения ax² + bx + c = 0
octave:9> function [x1,x2] = quadr(a, b, c) > D = sqrt(b^2-4*a*c); > x1 = (-b-D)/(2*a); > x2 = (-b+D)/(2*a); > endfunction octave:10> [y1,y2]=quadr(a, b, c) y1 = 2 y2 = 3
Графический интерфейс
Вообще-то, мы тут за математику командной строки гутарим, но пока непонятно как вывести на экран график функции. Впрочем, никакого секрета тут нет — для этих целей используется Gnuplot. Так можно изобразить Аттрактор Лоренца, установив дополнительный пакет odepkg.
function [vyd] = froessler (vt, vx) vyd = [- ( vx(2) + vx(3) ); vx(1) + 0.2 * vx(2); 0.2 + vx(1) * vx(3) - 5.7 * vx(3)]; endfunction A = odeset ('MaxStep', 1e-1); [t, y] = ode78 (@froessler, [0 70], [0.1 0.3 0.1], A); subplot (2, 2, 1); grid ('on'); plot (t, y(:,1), '-b;f_x(t);', t, y(:,2), '-g;f_y(t);', \ t, y(:,3), '-r;f_z(t);'); subplot (2, 2, 2); grid ('on'); plot (y(:,1), y(:,2), '-b;f_{xyz}(x, y);'); subplot (2, 2, 3); grid ('on'); plot (y(:,2), y(:,3), '-b;f_{xyz}(y, z);'); subplot (2, 2, 4); grid ('on'); plot3 (y(:,1), y(:,2), y(:,3), '-b;f_{xyz}(x, y, z);');
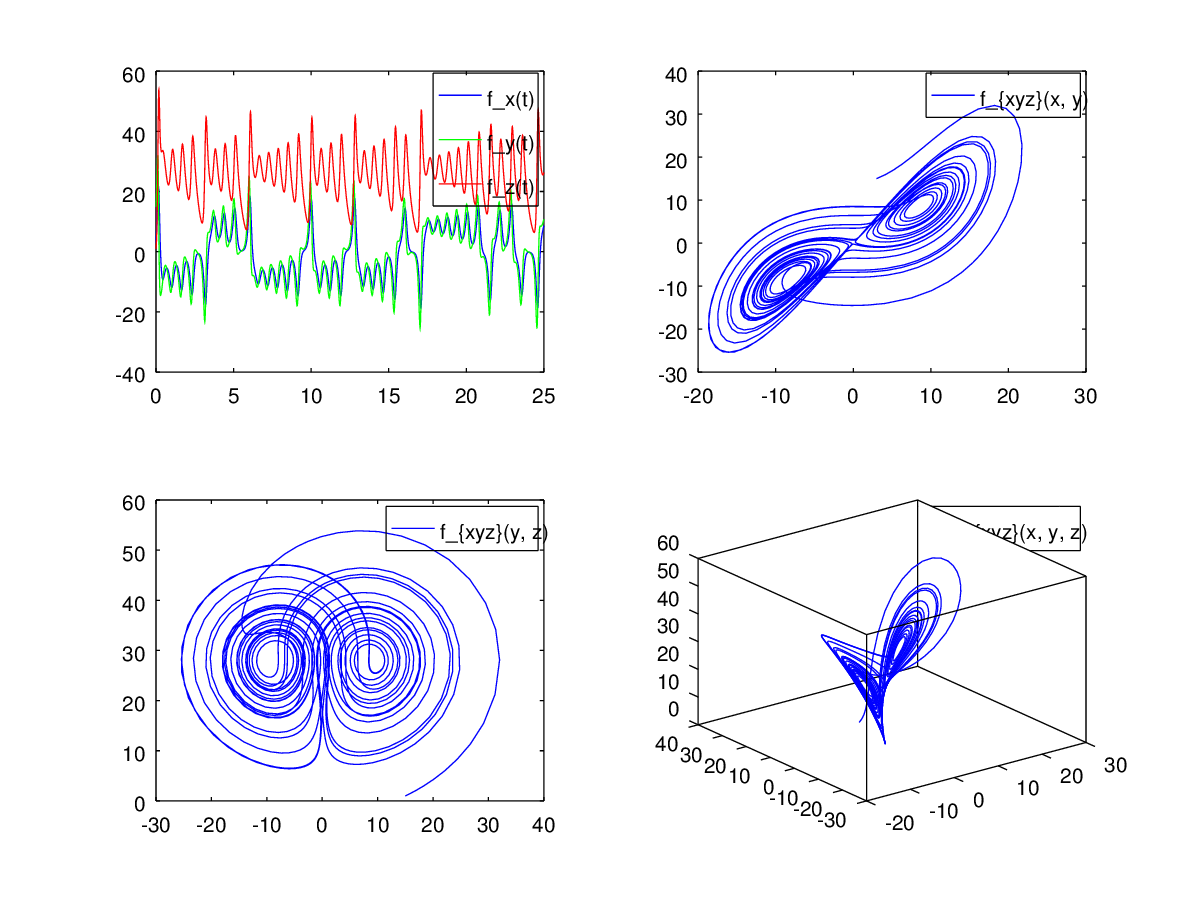
Наиболее удобной графической оболочкой для работы с Octave является программа QtOctave. Последняя уже стабилизировалась и включена в состав пакета с момента выхода Octave 4.0.
Что-же дальше?
Может возникнуть вопрос: а зачем вообще нужны открытые математические пакеты? Офисные приложения нужны всем, но ведь далеко не каждому необходимо сидя дома решать уравнения Пуассона, с помощью преобразования Лапласа. Для ВУЗ-ов MATLAB стоит значительно дешевле, нежели для физических лиц и коммерческих организаций. Коммерческие организации, если будет нужно, найдут денежные средства, а обычные люди пусть занимаются математикой в университетах или считают столбиком.
Конечно же, это ошибочное мнение. Научные расчеты, выполненные с использованием открытого ПО имеют дополнительный «уровень защиты», ведь при желании любой может повторить прогнать те же самые расчеты и проверить валидность результатов. Те же самые вычисления, выполненные на дорогущем ПО, частично отсекают возможность проверки результатов. Проблема на самом деле гораздо шире (английский текст) и дело не только в открытых или проприетарных математических программах. Не секрет, что научные журналы как правило не требуют от авторов предоставить данные и методику, достаточные для гарантированного повтора результатов эксперимента, проверки модели. Особенно часто этим грешат экономисты и финансисты, попросту засекречивая свои данные. Проверка расчетов и выводов среди выборки из массива статей с «засекреченными» данными дала неожиданные результаты (английский текст). Наука, как и софт, должна быть открытой, вот почему открытые математические пакеты имеют ценность для всего общества.
Рекомендуется к прочтению
Кроме последней книги, остальные материалы, использованные в статье, можно без труда найти в интернете. Половина из приведенных выше ссылок ведут на английские страницы. Буду рад вкратце сообщить о чем идет там речь или помочь с переводом.
- GNU Octave 4.0.1 Manual
- Алексеев Е.Р., Чеснокова О.В GNU Octave для студентов и преподавателей, 2011
- Н. Б. Шамрай Краткое руководство по работе с пакетами GNU Octave и Gnuplot, 2011
- Jesper Schmidt Hansen GNU Octave
