Мой любимый алгоритм: нахождение медианы за линейное время

Нахождение медианы списка может казаться тривиальной задачей, но её выполнение за линейное время требует серьёзного подхода. В этом посте я расскажу об одном из самых любимых мной алгоритмов — нахождении медианы списка за детерминированное линейное время с помощью медианы медиан. Хотя доказательство того, что этот алгоритм выполняется за линейное время, довольно сложно, сам пост будет понятен и читателям с начальным уровнем знаний об анализе алгоритмов.

Нахождение медианы за O(n log n)

Самым прямолинейным способом нахождения медианы является сортировка списка и выбор медианы по её индексу. Самая быстрая сортировка сравнением выполняется за O(n log n), поэтому от неё зависит время выполнения¹, ².

def nlogn_median(l):
    l = sorted(l)
    if len(l) % 2 == 1:
        return l[len(l) / 2]
    else:
        return 0.5 * (l[len(l) / 2 - 1] + l[len(l) / 2])

У этого способа самый простой код, но он определённо не самый быстрый.

Нахождение медианы за среднее время O(n)

Следующим нашим шагом будет нахождение медианы в среднем за линейное время, если нам будет везти. Этот алгоритм, называемый «quickselect», разработан Тони Хоаром, который также изобрёл алгоритм сортировки с похожим названием — quicksort. Это рекурсивный алгоритм, и он может находить любой элемент (не только медиану).

1. Выберем индекс списка. Способ выбора не важен, на практике вполне подходит и случайный. Элемент с этим индексом называется опорным элементом (pivot).
2. Разделим список на две группы:
   
   1. Элементы меньше или равные pivot, lesser_els
   2. Элементы строго большие, чем pivot, great_els
3. Мы знаем, что одна из этих групп содержит медиану. Предположим, что мы ищем k-тый элемент:
   
   • Если в lesser_els есть k или больше элементов, рекурсивно обходим список lesser_els в поисках k-того элемента.
   • Если в lesser_els меньше, чем k элементтов, рекурсивно обходим список greater_els. Вместо поиска k мы ищем k-len(lesser_els).

Вот пример алгоритма, выполняемого для 11 элементов:

Возьмём представленный ниже список. Мы хотим найти медиану.
l = [9,1,0,2,3,4,6,8,7,10,5]
len(l) == 11, поэтому мы ищем шестой наименьший элемент 
Сначала нам нужно выбрать опорный элемент (pivot). Мы случайным образом выбираем индекс 3. 
Значение элемента с этим индексом равно 2.

Разбиваем список на группы согласно pivot:
[1,0,2], [9,3,4,6,8,7,10,5]
Нам нужен шестой элемент. 6-len(left) = 3, поэтому нам нужен
третий наименьший элемент в правом массиве 

Теперь мы ищем третий наименьший элемент в следующем массиве:
[9,3,4,6,8,7,10,5]
Мы случайным образом выбираем индекс, который будет нашим pivot. 
Мы выбрали индекс 2, значение в котором равно l[2]=6

Разбиваем на группы согласно pivot:
[3,4,5,6] [9,7,10]
Нам нужен третий наименьший элемент, поэтому мы знаем, что это
третий наименьший элемент в левом массиве

Теперь мы ищем третий наименьший в следующем массиве:
[3,4,5,6]
Мы случайным образом выбираем индекс, который будет нашим pivot.
Мы выбрали индекс 1, значение в котором равно l[1]=4
Разбиваем на группы согласно pivot:
[3,4] [5,6]
Нам нужен третий наименьший элемент, поэтому мы знаем, что это
наименьший элемент в правом массиве.

Теперь мы ищем наименьший элемент в следующем массиве:
[5,6]

На этом этапе у нас есть базовый вариант, выбирающий наибольший
или наименьший элемент на основании индекса.
Нам нужен наименьший элемент, то есть 5.
return 5

Чтобы найти с помощью quickselect медиану, мы выделим quickselect в отдельную функцию. Наша функция quickselect_median будет вызывать quickselect с нужными индексами.

import random
def quickselect_median(l, pivot_fn=random.choice):
    if len(l) % 2 == 1:
        return quickselect(l, len(l) / 2, pivot_fn)
    else:
        return 0.5 * (quickselect(l, len(l) / 2 - 1, pivot_fn) +
                      quickselect(l, len(l) / 2, pivot_fn))


def quickselect(l, k, pivot_fn):
    """
    Выбираем k-тый элемент в списке l (с нулевой базой)
    :param l: список числовых данных
    :param k: индекс
    :param pivot_fn: функция выбора pivot, по умолчанию выбирает случайно
    :return: k-тый элемент l
    """
    if len(l) == 1:
        assert k == 0
        return l[0]

    pivot = pivot_fn(l)

    lows = [el for el in l if el < pivot]
    highs = [el for el in l if el > pivot]
    pivots = [el for el in l if el == pivot]

    if k < len(lows):
        return quickselect(lows, k, pivot_fn)
    elif k < len(lows) + len(pivots):
        # Нам повезло и мы угадали медиану
        return pivots[0]
    else:
        return quickselect(highs, k - len(lows) - len(pivots), pivot_fn)

В реальном мире Quickselect отлично себя проявляет: он почти не потребляет лишних ресурсов и выполняется в среднем за O(n). Давайте докажем это.

Доказательство среднего времени O(n)

В среднем pivot разбивает список на две приблизительно равных части. Поэтому каждая последующая рекурсия оперирует с ¹⁄₂ данных предыдущего шага.

Существует множество способов доказательства того, что этот ряд сходится к 2n. Вместо того, чтобы приводить их здесь, я сошлюсь на замечательную статью в Википедии, посвящённую этому бесконечному ряду.

Quickselect даёт нам линейную скорость, но только в среднем случае. Что, если нас не устраивает среднее, и мы хотим гарантированного выполнения алгоритма за линейное время?

Детерминированное O(n)

В предыдущем разделе я описал quickselect, алгоритм со средней скоростью O(n). «Среднее» в этом контексте означает, что в среднем алгоритм будет выполняться за O(n). С технической точки зрения, нам может очень не повезти: на каждом шаге мы можем выбирать в качестве pivot наибольший элемент. На каждом этапе мы сможем избавляться от одного элемента из списка, и в результате получим скорость O(n^2), а не O(n).

С учётом этого, нам нужен алгоритм для подбора опорных элементов. Нашей целью будет выбор за линейное время pivot, который в худшем случае удаляет достаточное количество элементов для обеспечения скорости O(n) при использовании его вместе с quickselect. Этот алгоритм был разработан в 1973 году Блумом (Blum), Флойдом (Floyd), Праттом (Pratt), Ривестом (Rivest) и Тарьяном (Tarjan). Если моего объяснения вам не хватит, то можете изучить их статью 1973 года. Вместо того, чтобы описывать алгоритм, я подробно прокомментирую мою реализацию на Python:

def pick_pivot(l):
    """
    Выбираем хорошй pivot в списке чисел l
    Этот алгоритм выполняется за время O(n).
    """
    assert len(l) > 0

    # Если элементов < 5, просто возвращаем медиану
    if len(l) < 5:
        # В этом случае мы возвращаемся к первой написанной нами функции медианы. 
        # Поскольку мы выполняем её только для списка из пяти или менее элементов, она не 
        # зависит от длины входных данных и может считаться постоянным
        # временем.
        return nlogn_median(l)

    # Сначала разделим l на группы по 5 элементов. O(n)
    chunks = chunked(l, 5)

    # Для простоты мы можем отбросить все группы, которые не являются полными. O(n)
    full_chunks = [chunk for chunk in chunks if len(chunk) == 5]


    # Затем мы сортируем каждый фрагмент. Каждая группа имеет фиксированную длину, поэтому каждая сортировка
    # занимает постоянное время. Поскольку у нас есть n/5 фрагментов, эта операция 
    # тоже O(n)
    sorted_groups = [sorted(chunk) for chunk in full_chunks]

    # Медиана каждого фрагмента имеет индекс 2
    medians = [chunk[2] for chunk in sorted_groups]

    # Возможно, я немного повторюсь, но я собираюсь доказать, что нахождение
    # медианы списка можно произвести за доказуемое O(n).
    # Мы находим медиану списка длиной n/5, поэтому эта операция также O(n)
    # Мы передаём нашу текущую функцию pick_pivot в качестве создателя pivot алгоритму
    # quickselect. O(n)
    median_of_medians = quickselect_median(medians, pick_pivot)
    return median_of_medians

def chunked(l, chunk_size):
    """Разделяем список `l` на фрагменты размером `chunk_size`."""
    return [l[i:i + chunk_size] for i in range(0, len(l), chunk_size)]

Давайте докажем, что медиана медиан является хорошим pivot. Нам поможет, если мы представим визуализацию нашего алгоритма выбора опорных элементов:


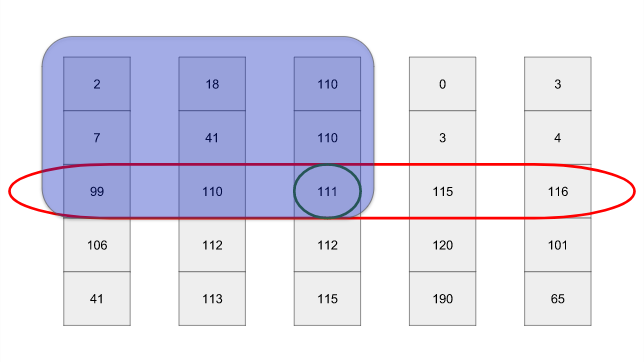
Красным овалом обозначены медианы фрагментов, а центральным кругом — медиана медиан. Не забывайте, мы хотим, чтобы pivot разделял список как можно ровнее. В худшем возможном случае каждый элемент в синем прямоугольнике (слева вверху) будет меньше или равен pivot. Верхний правый прямоугольник содержит ³⁄₅ половины строк — 3/5*1/2=3/10. Поэтому на каждом этапе мы избавляемся по крайней мере от 30% строк.

Но достаточно ли нам отбрасывать 30% элементов на каждом этапе? На каждом этапе наш алгоритм должен выполнять следующее:

• Выполнять работу O(n) по разбиению элементов
• Для рекурсии решать одну подзадачу размером в ⁷⁄₁₀ от исходной
• Для вычисления медианы медиан решать одну подзадачу размером с ¹⁄₅ от исходной

В результате мы получаем следующее уравнение полного времени выполнения T(n):

Не так уж просто доказать, почему это равно O(n). Быстрое решение заключается в том, чтобы положиться на основную теорему о рекуррентных соотношениях. Мы попадаем в третий случай теоремы, при котором работа на каждом уровне доминирует над работой подзадач. В этом случае общая работа будет просто равна работе на каждом уровне, то есть O(n).

Подводим итог

У нас есть quickselect, алгоритм, который находит медиану за линейное время при условии наличия достаточно хорошей опорного элемента. У нас есть алгоритм медианы медиан, алгоритм O(n) для выбора опорного элемента (который достаточно хорош для quickselect). Соединив их, мы получили алгоритм нахождения медианы (или n-ного элемента в списка) за линейное время!

Медианы за линейное время на практике

В реальном мире почти всегда достаточно случайного выбора медианы. Хотя подход с медианой медиан всё равно выполняется за линейное время, на практике его вычисление длится слишком долго. В стандартной библиотеке C++ используется алгоритм под названием introselect, в котором применено сочетание heapselect и quickselect; предел его выполнения O(n log n). Introselect позволяет использовать обычно быстрый алгоритм с плохим верхним пределом в сочетании с алгоритмом, который медленнее на практике, но имеет хороший верхний предел. Реализации начинают с быстрого алгоритма, но возвращаются к более медленному, если не могут выбрать эффективные опорные элементы.

В завершение приведу сравнение элементов, используемых в каждой из реализаций. Это не скорость выполнения, а общее количество элементов, которые рассматривает функция quickselect. Здесь не учитывается работа по вычислению медианы медиан.


Именно этого мы и ожидали! Детерминированный опорный элемент почти всегда рассматривает при quickselect меньшее количество элементов, чем случайный. Иногда нам везёт и мы угадываем pivot с первой попытки, что проявляется как впадины на зелёной линии. Математика работает!

---

1. Это может стать интересным применением поразрядной сортировки (radix sort), если вам нужно найти медиану в списке целых чисел, каждое из которых меньше 2³².
2. На самом деле в Python используется Timsort, впечатляющее сочетание теоретических пределов и практической скорости. Заметки о списках в Python.