How to become an author
Search
Write a publication
Pull to refresh

Решение задачи о приближении иррациональных

Reading time36 min
Views19K
Entertaining tasksMathematics*Programming*
В данной статье рассматриваются различные методы приближений иррациональных чисел, а также попутно затрагиваются вопросы, косвенно связанные с этой темой


В сборнике Арнольда есть следующая задача

38. Вычислить сумму:

$\frac{ 1 }{ 1\cdot2 } + \frac{ 1 }{ 2\cdot3 } + \frac{ 1 }{ 3\cdot4 } + ... + \frac{ 1 }{ 99\cdot100 }$


(с ошибкой не более 1% от ответа)

Ниже представлен алгоритм для вычисления частичных сумм этого ряда на языке Scheme (Lisp), который позволяет производить вычисления в обыкновенных дробях

#lang racket
(define series_sum
 ( lambda (n)
  (if (= n 0) 0
    (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1)))
  ) ) )
(series_sum 10)
(series_sum 100)
(series_sum 1000)
(series_sum 10000)
(series_sum 100000)
(series_sum 1000000)

(define series_sum_1
 ( lambda (n)
  (if (= n 0) 0 
    (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0)))
  ) ) )
(series_sum_1 10)
(series_sum_1 100)
(series_sum_1 1000)
(series_sum_1 10000)
(series_sum_1 100000)
(series_sum_1 1000000)


Два последних примера drRacket вычислил с ошибкой



#python
def series_sum(n):
	if n==0:
		return 0
	else:
		return 1.0/(n*(n+1.0))+series_sum(n-1.0)
 
print(series_sum(10))
print(series_sum(100))


Для перевода периодической десятичной дроби $ 0,(90) $ в обыкновенную
$ x=0,(90) $
домножим обе части на $ 10^{n} $, где $ n $ равняется периоду десятичной дроби
$ 100x=90,(90) $
вычтем из данного равенства предыдущее
$ 99x=90 \rightarrow\ x=\frac{90}{99}=\frac{10}{11} $

Можно заметить, что частичная сумма первых $n $ слагаемых $ s_{n} = \frac{ n }{ n + 1 } $

Доказательство по индукции
1. При $ n=1 $ гипотеза верна, так как $ s_{1}= \frac{ 1 }{ 2 }$
2. Предположим, что гипотеза верна и для $n=k $, т.е. что

$ s_{k}= \frac{ 1 }{ 1\cdot2 } + \frac{1}{2\cdot3}+...+\frac{1}{k(k+1)}=\frac{k}{k+1} $


где $ k $ — некоторое натуральное число
Установим справедливость и при $ n=k+1 $

$ s_{k+1}= \frac{ k+1 }{ k+2 } $


$ s_{k+1}=s_{k} + \frac{ 1 }{ (k+1)(k+2) } = \frac{k}{k+1} + \frac{1}{(k+1)(k+2)} =\frac{k^{2}+2k+1}{(k+1)(k+2)}=\frac{k+1}{k+2} $


Доказательство методом перебора
Пусть дана последовательность $ a_{1},a_{2},a_{3}, \: ...,a_{n}=\frac{1}{n(n+1)}$

Предположим, что частичная сумма первых $ n$ слагаемых $ s_{n}=\frac{n}{n+1}$
Тогда $ \frac{n}{n+1}-\frac{1}{n(n+1)}=\frac{n-1}{n}=s_{n-1}$
Отсюда
$ s_{n-1}-a_{n-1}=s_{n-2}$
$ s_{n-2}-a_{n-2}=s_{n-3}$
$ s_{n-3}-a_{n-3}=s_{n-4}$ и так далее
Пятясь назад, придём к $ s_{2}-a_{2}=\frac{1}{2}=s_{1}=a_{1} $

Теорема Вейерштрасса гласит
Если последовательность монотонна и ограничена, то она сходится
данная последовательность возрастает, поскольку $ s_{n}>s_{n-1} $
данная последовательность ограничена сверху, поскольку
$ s_{n}=\frac{n}{n+1}=1-\frac{1}{n+1} $

отобразим целочисленные координаты оси $ x$ на график функции
$ y=\frac{x}{x+1} $
отобразим полученные точки на график функции $ y=x$
получим систему вложенных отрезков с неподвижной точкой $ A$

$ [A,B]\supset[A,C]\supset [A,D]\supset [A,E]\supset [A,F]\supset... $


Кстати, любую дробь $ \frac{m}{n} $, где $ 0<\frac{m}{n}<1 $
можно представить частичной суммой («Квант» 1970)

$ S_{n}= \frac{1}{q_{1}q_{2}}+\frac{1}{q_{2}q_{3}}+\frac{1}{q_{3}q_{4}}+...+\frac{1}{q_{n}q_{n+1}} $,
где $ q_{n+1}-q_{n}=k, \: k\in\mathbb{N} $

$ S_{n}=\frac{1}{q_{1}}+\frac{1}{q_{2}}+\frac{1}{q_{3}}+...+\frac{1}{q_{n-1}}+\frac{1}{q_{n}}, $
где $ q_{n+1}:q_{n}=k, \: k \in \mathbb{N} $

$\frac{1}{2}+\frac{1}{6}=\frac{2}{3}$
$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}=\frac{3}{4}$
$\frac{1}{3}+\frac{1}{15}=\frac{2}{5}$ $\frac{1}{2}+\frac{1}{10}=\frac{3}{5}$ $\frac{1}{2}+\frac{1}{4}+\frac{1}{20}=\frac{4}{5}$
$\frac{1}{2}+\frac{1}{4}+\frac{1}{12}=\frac{5}{6}$
$\frac{1}{4}+\frac{1}{28}=\frac{2}{7}$ $\frac{1}{3}+\frac{1}{12}+\frac{1}{84}=\frac{3}{7}$ $\frac{1}{2}+\frac{1}{14}=\frac{4}{7}$ $\frac{1}{2}+\frac{1}{6}+\frac{1}{24}+\frac{1}{168}= \frac{5}{7}$
$\frac{1}{3}+\frac{1}{24}=\frac{3}{8}$ $\frac{1}{2}+ \frac{1}{8} =\frac{5}{8}$


Числа Фибоначчи


В следующей задаче требуется найти НОД двух соседних чисел Фибоначчи
43.Числа кроликов («Фибоначчи»), образуют последовательность $(a_{1}=1, 1, 2, 3, 5, 8, 13, 21, 34, ..., $ в которой $ a_{n+2} = a_{n+1} + a_{n} $ для всякого $ n = 1, 2, ... $. Найти наибольший общий делитель чисел $ a_{100} $ и $ a_{99} $.

Для решения данной задачи достаточно доказать, что два соседних числа Фибоначчи взаимно просты, то есть доказать справедливость тождества $ НОД(a_{n+1},a_{n}) = 1 $

Доказательство из книги «За страницами учебника математики» [10-11]
Из равенства $ u_{n+2} = u_{n+1} + u_{n} $ следует, что $ НОД(u_{n+2},u_{n+1}) = НОД(u_{n+1},u_{n})$. Пятясь таким образом назад, придём к $ НОД(u_{2},u_{1}) = НОД(1,1) = 1 $, а потому два соседних числа Фибоначчи взаимно просты.


Добавлю, что
$ НОД(u_{n+2},u_{n+1}) = НОД(u_{n+1},u_{n})$ по алгоритму Евклида
$НОД(u_{n+2},u_{n+1}) = НОД(u_{n+1},r)$
где $ r $ — остаток от деления $u_{n+2} $ на $ u_{n+1}$
и в данном конкретном случае $ r = u_{n}$ поскольку $ u_{n+2} = u_{n+1} + u_{n} $

Доказательство из книги «Числа Фибоначчи» Воробьёва
Пусть некоторое число $ d $ является делителем чисел $ u_{n} $ и $ u_{n+1} $. Тогда и их разность $ u_{n+1}-u_{n} = u_{n-1} $ будет делиться на $ d $.
Пятясь таким образом назад, придём к тому, что на $ d $ будут делиться и $ u_{n-2} $ и $ u_{n-3} $ и так далее, а значит и $u_{1}=1$ должно делиться на $ d $, а значит два соседних числа Фибоначчи взаимно просты


Тожество Кассини


Похожий метод, метод перебора последовательности $ F_{n} $ можно применить для доказательства тождества Кассини, которое выражается соотношением:
$ F_{n+1}F_{n-1}-F_{n}^2= (-1)^n $

Предположим, что
$ F_{n+1}F_{n-1}-F_{n}^2=F_{n-1}^2-F_{n}F_{n-2} $
Перебрав последовательность в обратном направлении, придём к тому, что левая и правая части данного равенства обе тождественны единице

Доказательство


Домножим тождество $ F_{n+1}=F_{n}+F_{n-1}$ на $ F_{n-1} $:
$ F_{n+1}F_{n-1} = F_{n}F_{n-1}+F_{n-1}^2 $

Вычтем $ F_{n}^2 $:
$ F_{n+1}F_{n-1}-F_{n}^2=F_{n }F_{n-1}+F_{n-1}^2-F_{n}^2 $
$ F_{n+1}F_{n-1}-F_{n}^2=F_{n-1}^2-F_{n}^2+F_{n}F_{n-1} $
$ F_{n+1}F_{n-1}-F_{n}^2=F_{n-1}^2-F_{n}(F_{n}-F_{n-1}) $
$ F_{n+1}F_{n-1}-F_{n}^2=F_{n-1}^2-F_{n}F_{n-2} $
$ F_{n+1}F_{n-1}-F_{n}^2=-(F_{n}F_{n-2}-F_{n-1}^2) $
Данное выражение показывает, что некая величина, которой тождественны левая и правая части равенства, меняет свой знак на противоположный при переходе $ n \rightarrow n-1 $

$ F_{1} \rightarrow F_{2}: $
$ F_{1}F_{3}-F_{2}^2=-(F_{3}^2-F_{2}F_{4})=F_{2}F_{4}-F_{3}^2 $
$ F_{2} \rightarrow F_{3}: $
$ F_{2}F_{4}-F_{3}^2=-(F_{5}F_{3}-F_{4}^2)=F_{4}^2-F_{5}F_{3} $
$ F_{3} \rightarrow F_{4}: $
$ F_{4}^2-F_{5}F_{3}=-(F_{5}^2-F_{6}F_{4})=F_{6}F_{4}-F_{5}^2 $
и т.д.

Приближения к золотому сечению


В следующей задаче необходимо вычислить золотое сечение, $ \frac {\sqrt{5} + 1}{2} \approx 1,618 $. [Это соотношение сторон открытки, остающейся себе подобной при отрезании квадрата, стороной которого является меньшая сторона открытки.]

53. Для последовательности чисел Фибоначчи $a_{n}$ задачи 43 найти предел отношения $ \frac { a_{n+1} }{ a_{n} } $ при стремлении $ n $ к бесконечности:

$ \frac { a_{n+1} }{ a_{n} } = 2, \frac {3}{2}, \frac {5}{3}, \frac {8}{5}, \frac {13}{8},\frac {21}{13}, \frac {34}{21}. $



Отметим на числовой оси отрезки


Числа $ x_{n} $ с чётными номерами представляют растущую последовательность

$\frac{ 3 }{ 2 } < \frac{ 8 }{ 5 } < \frac{ 21 }{ 13 }< ... $



Числа $ y_{n} $ с нечётными номерами представляют убывающую последовательность

$ 2 > \frac{ 5 }{ 3 } > \frac{ 13 }{ 8 }> ... $



По лемме о вложенных промежутках (Курс дифференциального и интегрального исчисления, 38)

$ \varphi = \lim x_{n} = \lim y_{n} $


А значит $ \varphi = \frac { a_{n+2} }{ a_{n+1} } = \frac { a_{n+1} }{ a_{n} } $

Разделив $ a_{n+2} = a_{n+1} + a_{n} $ на $ a_{n+1} $, получим уравнение $ \frac{a_{n+2}}{a_{n+1}} = 1 + \frac{a_{n}}{a_{n+1}} $
После замены
$ \frac{a_{n+2}}{a_{n+1}}=\varphi $
$ \frac{a_{n}}{a_{n+1}} = \frac{1}{\varphi} $
получится квадратное уравнение $ \varphi = 1 + \frac{1}{\varphi} $, положительным решением которого является золотое сечение
Различные методы решения этого уравнения приводятся ниже, в отдельном разделе, посвящённом решению квадратных уравнений

Если в программе geogebra соединить дугами окружности точки 2 и $ \frac{3}{2}$, $ \frac{3}{2}$ и $ \frac{5}{3}$, $ \frac{5}{3}$ и $ \frac{8}{5}$ и т.д. — получим самоподобную фигуру

Для сравнения



Кстати, в правильной пятиконечной звезде (звёздчатом пятиугольнике) каждый отрезок делится другим отрезком, пересекающим его, в золотом сечении

В самом деле, так как треугольники ACD и ABE подобны, то AC:AB=AD:AE. Но AD=BC, а AE=AC, и поэтому AC:AB=BC:AC — уже известная нам пропорция золотого сечения.

В правильном пятиугольнике отношение диагонали к стороне также равно $\varphi $

Вообще, существует стандартный алгоритм вычисления чисел Фибоначчи на Python
Этот алгоритм представлен на сайте Python.org 
def fib(n):
	    a, b = 0, 1
	    while a < n:
		print(a)
		a, b = b, a+b
fib(100)

Приближения к $ \varphi $ являются отношением суммы двух соседних чисел $a$ и $b$ к числу $ b $ 
def fib(n):
	    a, b = 0.0 , 1.0
	    while a < n:
		print((a+b)/b)
		a, b = b, a+b
fib(12)

На двенадцатом шаге получим приближение, равное 1.61805

Формула Бине использует $\varphi $ для вычисления $n$-ого числа Фибоначчи
$ F_{n}=\frac{(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n}{\sqrt {5}} $
Можно заметить, что второе слагаемое всегда меньше единицы при любом целом неотрицательном $n$
Поэтому, зная, что формула Бине даёт целые числа, можно утверждать справедливость тождества, в котором данная дробь округляется до ближайшего целого
$ F_{n}=\frac{(\frac{1+\sqrt{5}}{2})^n}{\sqrt{5}}$


Пусть $ j^2=5 $
Тогда выражения вида $ (a+bj)(1+j) $ будут принадлежать множеству
$ a+bj (a,b \in \mathbb{N})$ поскольку
$ (a+bj)(1+j)=(a+5b)+(a+b)j $
то есть $ a_{n+1}=a_{n}+5b_{n},b_{n+1}=a_{n}+b_{n} $
Приняв $ a=b=1 $
получим приближение
$ F_{2} \approx \frac{(1+j)(1+j)}{j2^2}=\frac{6+2j}{4j} \approx 1.17 $

$ F_{n+1} \approx \frac{(a_{n}+b_{n}j)(1+j)}{j2^n} $

Алгоритм вычисления $ a,b,2^{n} $ 
#python
a=b=1
t=2
for i in range(n):
    A=a+5*b
    B=a+b
    t=t*2
    a=A
    b=B
print ((a+b*5**0.5)/(t*5**0.5))
#n=10 Fn=88.99775275224582




Цепные дроби


Если в уравнении $ x = 1 + \frac{1}{x} $ в правой части заменить x на $ 1 + \frac{1}{x} $ получим $ x = 1 + \frac{1}{1 + \frac{1}{x}} $
Продолжая производить замены, придём к представлению золотого сечения в виде цепной дроби

$1+ \frac{1}{1 + \frac{1}{1+ \frac{1}{1+ \frac{1}{1+ \frac{1}{1+...}}}}}$



Задача из учебника SICP
Упражнение 1.35.
Покажите, что золотое сечение $ \varphi $ (раздел 1.2.2) есть неподвижная точка трансформации $ x \to 1 + 1/x $, и используйте этот факт для вычисления $\varphi $ с помощью процедуры fixed-point.

пример вычисления факториала
(define ! 
 (lambda (n) 
  (if (= n 0) 
    1 
    (* n (! (- n 1))))))
(display (! 5))


Алгоритм решения задачи 1.35 
(define fixed-point 
 (lambda (n) 
  (if (> n 10) 
    1 
    (+ 1 (/ 1.0 (fixed-point (+ n 1)))))))
(display (fixed-point 1) )


Сперва опишем счётчик, инкрементирующий переменную $ i $ в цикле 
(do ((i 1 (+ 1 i)))
    ((> i 10))
  (display i)(newline))

Оператор set! позволяет переопределить значение глобальной переменной
Определим глобальную переменную fixed-point и будем переопределять значение данной переменной в цикле do c помощью оператора set!
(define fixed-point 1)
(do ((i 1 (+ 1 i)))
    ((> i 10))
   (set! fixed-point (+ 1 (/ 1.0 fixed-point)))   
  (display fixed-point)
  (newline))



#python
arr=[1.0]
def foo(a):
	b=1.0+1.0/(1.0+1.0/a[len(a)-1])
	return b
arr.append(foo(arr)) #первый шаг
arr.append(foo(arr)) #второй шаг
arr.append(foo(arr)) #третий шаг
print (arr)


Задачник Арнольда
54. Вычислить бесконечную цепную дробь

$1+ \frac{1}{2 + \frac{1}{1+ \frac{1}{2+ \frac{1}{1+ \frac{1}{2+...}}}}}$



Решение
Рассмотрим уравнение

$ \alpha = 1+ \frac{1}{2 + \frac{1}{ \alpha}}$


Согласно теоремам 236 и 235 из книги «Теория чисел»:

$ \alpha = \frac{ P_{1}\alpha+ P_{0}}{Q_{1}\alpha+ Q_{0} } $


Составляем таблицу значений $ P_{n} $ и $ Q_{n} $ при $ n=0,1:$

1 2
P 1 3
Q 1 2


так что $\alpha = \frac{ 3\alpha + 1 }{ 2\alpha + 1}, 2\alpha^{2} - 2\alpha -1 = 0$

и поскольку $ \alpha > 0 ,$ то

$ \alpha = \frac{ 1 + \sqrt{3} }{ 2 } $




Пусть дана последовательность
$x_{n}=\sqrt{a \sqrt{a \sqrt{a ...\sqrt{a}}}}, $ образованная умножением подкоренного выражения на радикал $ \sqrt{a}$
Для этой последовательности справедливо равенство
$ x_{n+1}^2=ax_{n} $
Далее надо доказать само существование предела $ \lim_{n\to\infty}\frac{x_{n+1}^2}{x_{n}}$
поскольку, если этот предел существует, то он должен равняться числу $ a $
Для доказательства существования применим аксиому Больцано-Вейерштрасса. В самом деле, можно доказать по индукции, что при любом $ n $
$ x_{n}<x_{n+1}<a $
Поэтому последовательность $ {x_{n}}$ монотонна и ограничена


Здесь показатели степеней представляют геометрическую прогрессию, то есть
$ a^\frac{1}{2} \cdot a^\frac{1}{4} \cdot a^\frac{1}{8} ... $
При перемножении степеней с одинаковыми основаниями показатели степеней складываются

$ a^{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+... } $


Сумма геометрической прогрессии $ s_{n} = \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...=1 $
Легко понять, что $ s_{n} $ отличается от $ 1 $ на
$ (\frac{1}{2})^n $ и что эта разность становится сколь угодно малой или «стремится к нулю» при неограниченном возрастании $ n$


На рисунке ниже $ (a,a)$ является неподвижной точкой системы вложенных отрезков, высекаемых графиками функций $ y= x^{s_{n}}$ на прямой $ x=a $ (а также системы, высекаемой на прямой $y=a$)


#python
def foo(n,a):
 	temp=a
 	while(n>0):
 		a=temp*(a**0.5) #a=temp+(a**0.5)
 		n=n-1
 	return a**0.5
 print(foo(50,2))
#1.9999999999999993


Если уравнение $ \varphi^2-\varphi-1=0 $ переписать в виде $ \varphi^2 = 1 +\varphi, $ то заменяя $ \varphi $ под корнем на $ \sqrt{1+\varphi}, $ получим $ \varphi=\sqrt{1+\sqrt{1+\varphi}} $
Тогда
$ \varphi=\sqrt{1+ \sqrt{1 +\sqrt{1 + ...} } }$

Данное выражение является частным случаем варианты $ x_{n} = \sqrt{c+ \sqrt{c +... + \sqrt{c } } } $
Курс дифференциального и интегрального исчисления, 35 (2)
Таким образом $ x_{n+1}$ получается из $ x_{n}$ по формуле

$ x_{n+1} = \sqrt{c + x_{n} } $


… По основной теореме, варианта $ x_{n}$ имеет некий конечный предел $ a $. Для определения его перейдём к пределу в равенстве

$ x_{n+1}^{2} = c + x_{n}; $


Мы получим, таким образом, что $ a $ удовлетворяет квадратному уравнению

$ a^{2} = c + a $


Уравнение это имеет корни разных знаков; но интересующий нас предел $ a $ не может быть отрицательным, следовательно, равен именно положительному корню:

$ a = \frac{ \sqrt{4c + 1} + 1}{2} $



То есть $ \varphi $ является одним из бесконечного множества пределов: корней уравнения $ a^{2} = c + a $ при различных $ c $

Далее в «Курсе дифференциального и интегрального исчисления», 35(3) рассматривается алгоритм вычисления обратного числа (такого числа 1/с, произведение которого на данное число с равно единице)
Пусть $ c $ — любое положительное число, и положим $ x_{n} = cy_{n} $
Написанное выше рекуррентное соотношение заменится таким:

$ y_{n+1} = y_{n}(2 - cy_{n}) $


Взяв начальное значение $ y_{0} $ под условием: $ 0< y_{0}<\frac{1}{c} $, получим, что $ y_{n} $, монотонно возрастая, будет стремиться к $ \frac{1}{c} $. По этой схеме на счётных машинах и вычисляется число, обратное $ c $. 


#python
def reciprocal(c,y0,n):
	arr=[]
	for i in range(n):
		arr.append(y0)
		y0=y0*(2-c*y0)
        return arr


Функция reciprocal принимает на вход число $ c $, начальное значение $ y_{0} $, количество итераций $ n $ и возвращает массив приближений к числу $ \frac{1}{c} $.
$ y_{0} = 0.1 $ при $ c<10 $
$ y_{0} = 0.01 $ при $ 10<c<100 $
$ y_{0} = 0.001 $ при $ 100<c<1000 $
и т.д.
Примеры работы функции reciprocal при подстановке в переменную $ c $ чисел 3,5 и 8

>>> reciprocal(3,0.1,5)
[0.1,   0.17,   0.2533,   0.31411733000000003,   0.3322255689810133]
>>> reciprocal(5,0.1,5)
[0.1,0.15000000000000002,0.18750000000000003,0.19921875000000003,0.19999694824218753]
>>> reciprocal(8,0.1,5)
[0.1,0.12,0.1248,0.12499968,0.1249999999991808]


Геометрическое представление о данном алгоритме даёт метод Ньютона или метод касательных

Пусть дано уравнение прямой

$ y=kx+b $


Уравнение прямой, проходящей через точку $ (x_{0},y_{0}) $

$ y_{0}=kx_{0}+b $


Тогда

$ y-y_{0}=kx - kx_{0}$


$y=k(x-x_{0})+f(x_{0})$


Так как угловой коэффициент касательной к графику дифференцируемой функции в точке с абсциссой $ x_{0}$ равен $ f'(x_{0}) $, то уравнение касательной имеет вид

$ y=f'(x_{0})(x-x_{0})+f(x_0) $



Производной функции $ y=f(x) $ называется предел отношения приращения функции $ \Delta y $ к приращению аргумента $ \Delta x $:

$ y'= \lim_{\Delta x\to 0} \frac{ \Delta y }{ \Delta x } =\lim_{\Delta x\to 0} \frac{ f(x_{0}+\Delta x)-f(x_{0}) }{ \Delta x } $


Для гиперболы $ y=\frac{1}{x} $

$ f(x+ \Delta x) = \frac{1}{x+ \Delta x} $


$ \Delta y = \frac{1}{x + \Delta x} - \frac{1}{x} = \frac{- \Delta x}{x(x+ \Delta x)} $


$ \frac{ \Delta y }{ \Delta x } = \frac{- \Delta x}{x(x+\Delta x)\Delta x}= \frac{-1}{x(x+ \Delta x)}$


Знаменатель состоит из двух слагаемых, второе при малых значениях $ \Delta x $ пренебрежимо мало по сравнению с первым, значит

$ \lim_{\Delta x\to 0}\frac{-1}{x^2+x\Delta x}=-\frac{1}{x^2} $



Касательными $ y=f'(x_{0})(x-x_{0})+ f(x_{0})$ к гиперболе $ y=\frac{1}{x} $ являются функции
$ y=-\frac{x-x_{0}}{x_{0}^2}+\frac{1}{x_{0}} \rightarrow y=\frac{2x_{0}-x}{x_{0}^2}$, то есть
$ y = \frac{2}{x_{0}} - \frac{x}{x_{0}^{2}} $

Подставляя числа $ 1,2,3,4, ...$ вместо $ x_{0} $ получим уравнения касательных

$ y=2-x $


$ y=1-\frac{x}{4} $


$ y=\frac{2}{3}-\frac{x}{9} $


$ y=\frac{1}{2}-\frac{x}{16} $





Если сдвинуть гиперболу вниз на $ c $, то она пересечёт ось абсцисс в точке $ \frac{1}{c} $
Уравнение касательных преобразуется в $ y = \frac{2}{x_{0}} - \frac{x}{x_{0}^{2}} - c $
Далее, приравняв уравнение касательной к нулю и выразив $ x $, получим уравнение $ x= x_{0} - \frac{f(x_{0})}{f'(x_{0})}$

Вместо $ f(x_{0}) $ подставим $ \frac{1}{x_{0}} - c $
Вместо $ f'(x_{0}) $ подставим $ -\frac{1}{x_{0}^{2}} $

Получим выражение $ x= x_{0} + (\frac{1}{x_{0}}-c) x_{0}^{2} $
Раскрыв скобки, получим $ x= x_{0} + x_{0}-c x_{0}^{2} $

Подставим $ 0.1 $ в уравнение $ x=x_{0}(2-c x_{0}) $ и посмотрим, какие значения будет принимать $ x $ по мере приближения к $ \frac{1}{c} $
Пусть $ c=2 $
Тогда округлённая обратная величина будет равна $ 0.1, 0.18, 0.29, 0.42, 0.49, 0.5 $

Подставим эти значения в уравнение $ y=\frac{2}{x_{0}}-\frac{x}{x_{0}^{2}}-2 $

Касательные

$ y= 0.111 - \frac{x}{0.897} $


$ y= 0.222 - \frac{x}{0.81} $


$ y= 0.816 - \frac{x}{0.504} $


$ y= 0.857 - \frac{x}{0.49} $


$ y= 1.5 - \frac{x}{0.326} $


$ y= 2 - \frac{x}{0.25} $


с каждой новой итерацией будут всё ближе к искомой величине



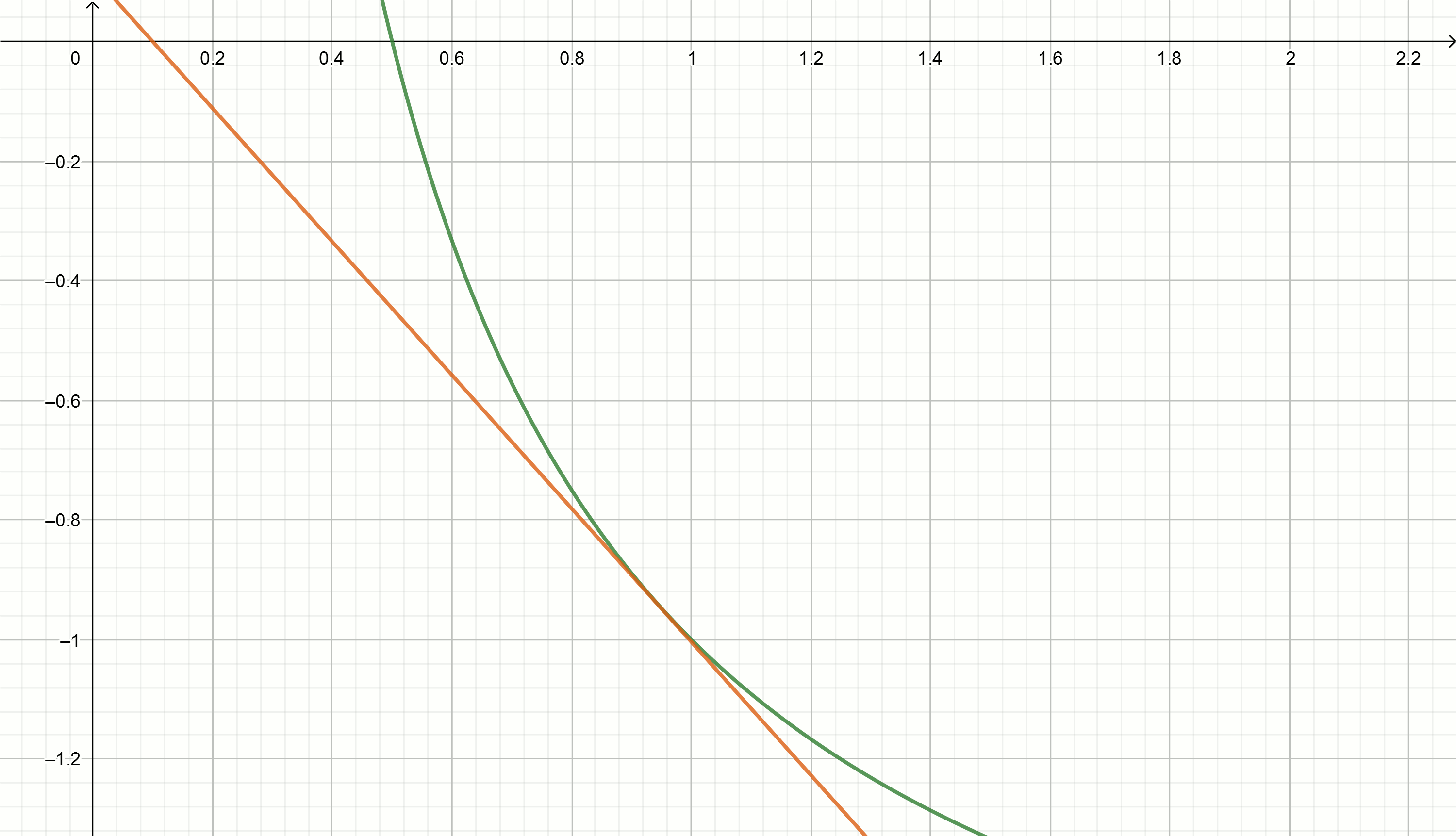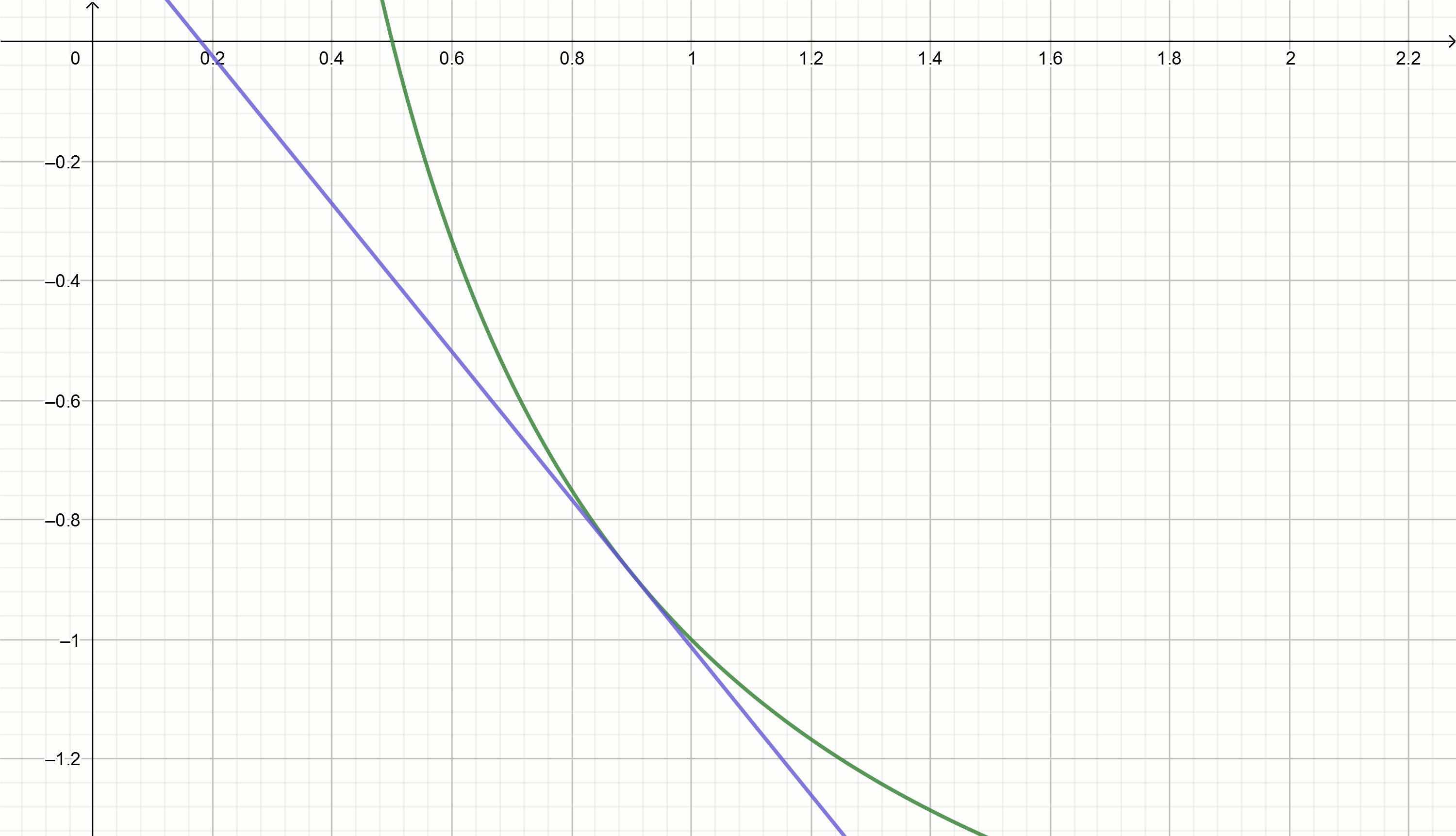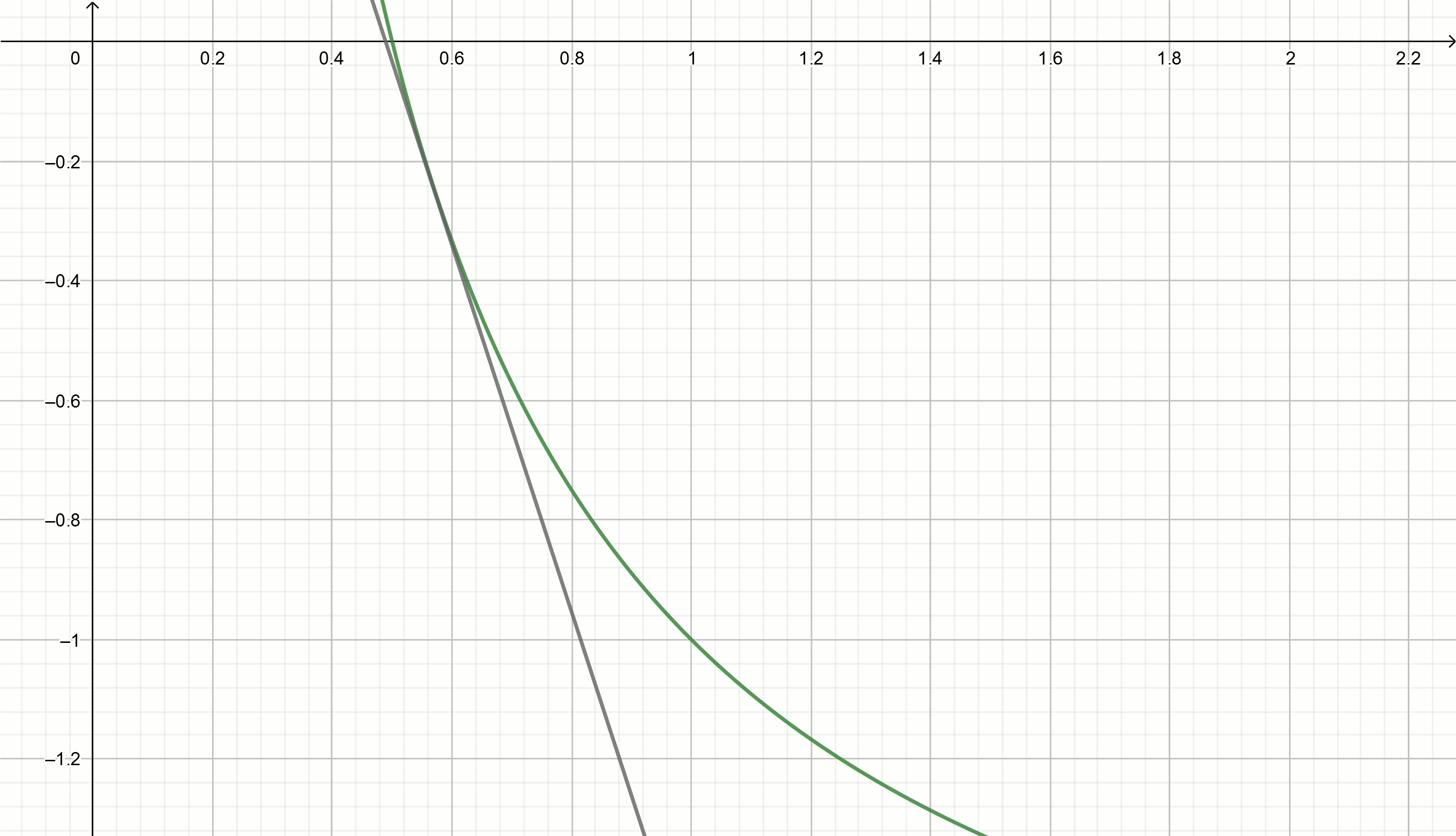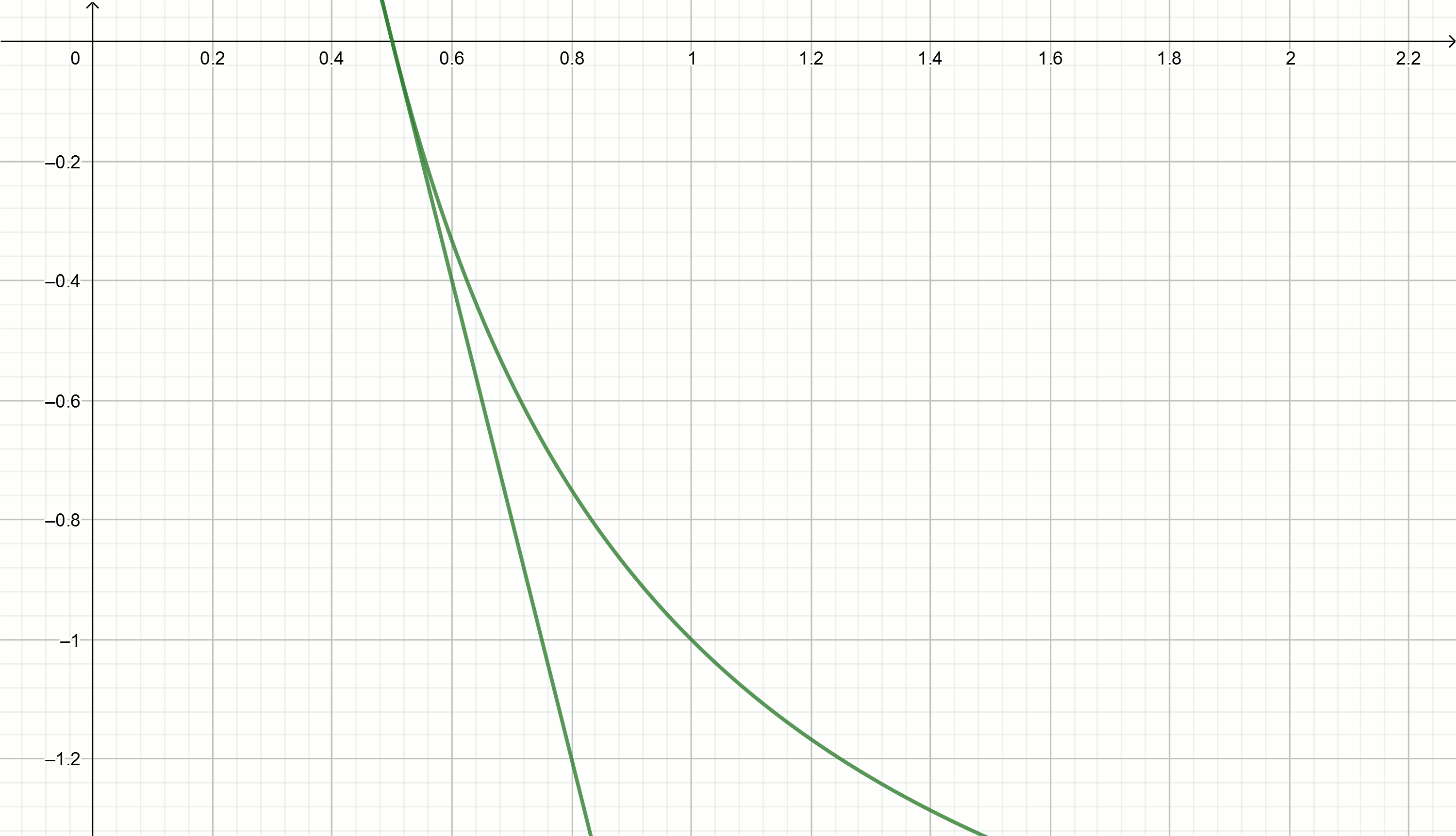
Заголовок спойлера

Модифицированный метод касательных


Преобразуем $ \frac{1}{x}-\alpha =0 \rightarrow \frac{1}{x}=\alpha \rightarrow 1=\alpha\cdot x $
$ \alpha\cdot x -1 =0 $
и возведём это уравнение в квадрат, чтобы получить квадратную параболу
$ \alpha^2 x^2 - 2\alpha x + 1 =0 $
Все параболы данного вида будут иметь с осью абсцисс одну общую точку (точку касания), равную $ \frac{1}{\alpha} $
Для того, чтобы найти приближения к точке касания, надо взять производную этой функции
Производная будет равна $ 2\alpha^2 x - 2 \alpha $
Тогда касательными к параболе будут функции вида

$ y = (2\alpha^2 x_{0} - 2 \alpha)(x-x_{0})+(\alpha^2 x_{0}^2-2\alpha x_{0} + 1) $


$ y = (2\alpha^2 x_{0} - 2 \alpha)x - \alpha^2 x_{0}^2 + 1 $



Пусть требуется найти приближения к $ \frac{1}{3} $
Тогда параболой будет функция $ 9x^{2}-6x+1 $

Касательными будут функции
$ y= (18 x_{0}-6)x-9x_{0}^2+1 $
В точке $ x_{0}=0 $ касательной будет $ -6x+1=0 $
Первым приближением будет $ \frac{1}{6} \approx 0.17 $
Подставив это значение в уравнение касательной, получим
$ y=-3x+ \frac{3}{4} $
Касательная пересечёт ось абсцисс в точке $ -3x+ \frac{3}{4}= 0 \rightarrow x=\frac{1}{4}=0.25 $
Приравняв $y $ к нулю и выразив $ x $ в уравнении касательной, получим уравнение, позволяющее получать новые приближения

$ x=\frac{9x_{0}^2-1}{18x_{0}-6} $



Напишем функцию, которая вычисляет данное значение при различных $ x_{0}$
#python
def foo(x_null):
    x=(9.0*x_null**2.0-1.0)/(18.0*x_null-6.0)
    return x 
print (foo(foo(foo(foo(foo(foo(foo(0))))))))



(define (foo x)( /(-(* 9 (* x x))1)(- (* 18 x)  6) ))
(display (foo(foo(foo(foo(foo(foo(foo 0))))))))

Добавим в функцию переменную, равную количеству рекурсивных вызовов функции

def foo(x_null,i):
    i=i-1
    x=(9.0*x_null**2.0-1.0)/(18.0*x_null-6.0)
    print(x)
    if i>=0:
        foo(x,i)
foo(0,7)

получим приближение, равное $ 0.33 $
Далее этот алгоритм используется для подсчёта приближений в обыкновенных дробях на Scheme

Обработка переменных в цикле производится следующим образом
(define (do_cycle n)
  (do ((i 1 (+ i 1))) ((> i n)  )
   (display i)(display " ")   ))
(do_cycle 10)

Далее do_cycle используется для вычисления приближений в цикле
(define (foo x)( /(-(* 9 (* x x))1)(- (* 18 x)  6) ))
(define x0 0)
(define (do_cycle n)
  (do ((i 1 (+ i 1))) ((> i n)  )
   (foo x0)(set! x0 (foo x0))   ))
(do_cycle 7)
(display x0)

Если ограничиться однократным вычислением производной в точке начального приближения, то пересечения прямых, параллельных касательной $ y=-6x+1 $ с осью абсцисс дадут новые приближения
Подставив значение $ -6x+1=0 \rightarrow x= \frac{1}{6} $ в уравнение параболы $ 9x^{2}-6x+1 $ получим значение, на которое требуется сдвинуть касательную

Новой касательной будет $ -6x+1+0.25=-6x+1.25 $

а следующим приближением будет точка пересечения этой касательной с осью абсцисс
$ x=1.25/6 $

Подставив это значение в уравнение параболы $ 9x^{2}-6x+1 $ получим значение, на которое необходимо сдвинуть касательную по оси ординат

Алгоритм
Пусть proxima — это последовательные приближения
b_coef — это коэффициент, на который сдвигается касательная по оси абсцисс
parabola() — это параболическая функция

proxima=0.17
b_coef=1.0
def parabola(x):
    return 9.0*x*x-6.0*x+1.0 
i=0
while i<=100000:
    b_coef = b_coef+parabola(proxima)
    proxima = b_coef/6.0
    i=i+1
print(proxima)

Результат $ \approx 0.3333 $

Предположим, что свободные коэффициенты касательных являются рациональными числами, то есть $ b \in \mathbb {Q} $. Тогда $ proxima \in \mathbb {Q} $, поскольку является результатом деления коэффициента $b$ на натуральное число
При подстановке proxima в $ y=(3x-1)^2 $ получим число рациональное. Тогда $ b \in \mathbb {Q} $ по предположению

В обыкновенных дробях
(define proxima 1/6)
(define b_coef 1)
(define (parabola x)(  +( -(* 9 (* x x))(* 6 x))1  ) )

(define (do_cycle n)
  (do ((i 1 (+ i 1))) ((> i n)  )
  (set! b_coef (+ b_coef (parabola x0)))
  (set! proxima (/ b_coef 6)) 
     ))
(do_cycle 5)
(display proxima)





Итерационный метод Герона для извлечения квадратного корня из числа $ a$ использует формулу

$ x_{n+1} = \frac{1}{2}(x_{n}+\frac{a}{x_{n}}) $



Пусть $ x^2 =a $, тогда $ x= \frac{a}{x} $
Пусть $ x_{1}$ равняется целой части $ \sqrt{a}$
Проведём горизонтальную прямую через точку $ y=x_1$
Прямая $ y=x_{1}$ пересечёт графики функции $ y=x$ и $ y=a/x $ в точках $ (x_{1},x_{1})$ и $(a/x_{1},x_{1}) $

Пусть точка $ x_{2}=\frac{1}{2}(x_{1}+\frac{a}{x_{1}})$ лежит на прямой $ y=x_{1}$
… точка $ x_{3}=\frac{1}{2}(x_{2}+\frac{a}{x_{2}})$ лежит на прямой $ y=a/x_{2}$
… точка $ x_{n}=\frac{1}{2}(x_{n-1}+\frac{a}{x_{n-1}})$ лежит на прямой $ y=a/x_{n-1}$
Последовательность $ x_{n}$ монотонна и ограничена, а значит сходится



Проецируя эти приближения на ось $ x$ получим систему вложенных отрезков
$ [x_{1},a/x_{1}] \supset [x_{2},a/x_{2}]\supset [x_{3},a/x_{3}]\supset...[x_{n},a/x_{n}]$ с неподвижной точкой $ \sqrt{a} $
Слева от $\sqrt{a}$ располагаются приближения по недостатку, справа приближения по избытку

Формулу Герона можно получить подстановкой $ k=2$ в формулу общего вида для вычисления корней степени $ k$

$ x=\frac{a+(k-1)x^k}{kx^{k-1}} $




В книге «Занимательная геометрия» сообщается другой старинный способ извлечения квадратного корня

Пусть надо вычислить $\sqrt{13} $. Он заключается между $3$ и $4$ и, следовательно, равен $3$ с дробью, которую обозначим через $x $.
Итак,
$\sqrt{13}=3+x $, откуда $13=9+6x+x^2 $
Квадрат дроби $x $ есть малая дробь, которую в первом приближении можно пренебречь, тогда имеем:
$13=9+6x $, откуда $6x=4 $ и $x=\frac{2}{3}=0,67$
Значит, приближенно $\sqrt{13}=3,67 $. Если мы хотим определить значение корня ещё точнее, напишем уравнение
$\sqrt{13}=3\frac{2}{3}+y $, где $y $-небольшая дробь, положительная или отрицательная. Отсюда
$13=\frac{121}{9}+\frac{22}{3}y+y^2 $. Отбросив $y^2 $, находим, что $y $ приближенно равен $-\frac{2}{33}=-0,66 $.
Следовательно, во втором приближении $\sqrt{13}=3,67-0,06=3,61 $.
Третье приближение находим тем же приемом и т.д.



Вычисление квадратного корня с помощью цепных дробей использовал Рафаэль Бомбелли

Чтобы найти значение $\sqrt{n}$, сначала определим его целое приближение: $\sqrt {n}=a\pm r $, где $ 0 < r < 1 $
Тогда $ n=(a\pm r)^{2}=a^{2}\pm 2ar+r^{2} $. Отсюда несложно вывести, что $ r={\frac {|n-a^{2}|}{2a\pm r}} $. Повторно подставляя полученное выражение в формулу $\sqrt {n}=a\pm r $, мы получаем разложение в цепную дробь:

$ a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm \cdots }}}}}} $




следующий алгоритм использует разложение в цепную дробь
#python
arr=[]
def square_root(n,a,n_count): # n-подкоренное значение, a - целая часть корня 
    x0=a                                # первое приближение равно a
    global arr
    for i in range(n_count): # результат будет больше искомой величины на a
        arr.append(x0-a)  # вычитаем a
        x0=2*a+(n-a*a)/x0


Способ выделения целой части позволяет представить иррациональное число в виде бесконечной цепной дроби с частыми числителями, равными единице
Вот пример разложения в цепную дробь числа $ \sqrt{5} $ из книги «Алгебра»

$ \sqrt{5}-2= \frac{(\sqrt{5}-2)(\sqrt{5}+2)}{\sqrt{5}+2}=\frac{1}{\sqrt{5}+2} $



Таким образом $ \sqrt{5} = 2+\frac{1}{\sqrt{5}+2} $

Выделим целую часть числа $ \sqrt{5}+2:E(\sqrt{5}+2)=4 $. Значит, $ \sqrt{5}+2 $ можно представить в виде $ 4 + \alpha $. Ясно, что $ \alpha = \sqrt{5}+2-4=\sqrt{5}-2 $, поэтому $ \sqrt{5}+2=4+\sqrt{5}+2$. Снова уничтожим иррациональность в числителе второго слагаемого:

$ \sqrt{5}-2 = \frac{1}{\sqrt{5}+2} $


В итоге получилось:

$ \sqrt{5} = 2 + \frac{1}{4+\frac{1}{\sqrt{5}+2}} $


Проделаем еще один аналогичный шаг:

$ \sqrt{5} = 2 + \frac{1}{4+\frac{1}{4+\frac{1}{\sqrt{5}+2}}} $


Нетрудно заметить, что процесс выделения целой части и образования цепной дроби в данном примере не имеет конца. В каждом новом знаменателе будет появляться $ 4 $ и слагаемое $ \sqrt{5}-2 $. Поэтому ясно, что $ \sqrt{5}$ представляется в виде бесконечной цепной дроби:

$ \sqrt{5} = [2, 4, 4, 4, ...] $




Гипотеза


Если $ d \in \mathbb{N}, \sqrt{d} \notin \mathbb{N}$, то цепная дробь числа $ \sqrt{d} + [\sqrt{d}] $ чисто периодическая.
Эту гипотезу доказал Эварист Галуа

Так чисто периодическая дробь $ [2,2,2,...]$ является суммой непериодической части дроби $[1;2,2,2,...] = \sqrt{2}$ и целой части $ [\sqrt{2}] =1 $

$\sqrt{3} = [1;1,2,...];$
$ \sqrt{3}+1 = [2,1,...] $

$\sqrt{5} = [2;4,4,4,...];$
$ \sqrt{5}+2 = [4,4,4,...] $

$\sqrt{6} = [2;2,4,...]; $
$ \sqrt{6}+2 = [4,2,...] $

$\sqrt{13} = [3;1,1,1,1,6,...];$
$ \sqrt{13}+3 = [6,1,1,1,1,...] $

Вычисление в облаке
WolframAlpfa производит вычисление цепных дробей с помощью операции continued fraction
Вычислим значение $ \sqrt{3} $
ссылка
Вычислим значение $\sqrt{3}+1$
ссылка

Если в разложении корня по методу Бомбелли

$ \sqrt{n} =a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm \cdots }}}}}} $


к первому слагаемому прибавить $ a $, получим чисто периодическую дробь

$ \sqrt{n}+a =2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm \cdots }}}}}} $



Остаётся привести дробь к виду, в котором числителями дробей являются единицы

Разделив числитель и знаменатель дроби на $ |n-a^{2}| $, получим выражение

$ \sqrt{n}+a =2 a\pm {\frac {1}{\frac{2a}{|n-a^{2}|} \pm {\frac {1}{2a \pm {\frac {1}{\frac{2a}{|n-a^{2}|}\pm \cdots }}}}}} $



$ \sqrt{13}+3 = 6+ \frac{1}{\frac{6}{4} + \frac{1}{6 + \frac{1}{\frac{6}{4}+...} } } =[6,\frac{3}{2},...] $


Алгоритм приближения цепной дроби $ [6,\frac{3}{2},...] $
#lang racket
(define continued_fraction
 ( lambda (n)
  (if (= n 0) 1 
    (+ 6 (/ 1  (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) 
  )))
(continued_fraction 4)

На четвёртом шаге получаем $ 6\frac{3818}{6305} $, что равно $ 6,6055511...$ в то время как $ \sqrt{13}+3 \approx 6.6055512... $.


Приближения к корню из натурального числа методом Ньютона
Итерационную формулу Герона можно получить методом Ньютона, проводя касательные к параболе $ y=x^2-a$

Подставим $ f(x)=x^2-a$ и $ f'(x)=2x$ в уравнение $ x_{1} = x_{0}-\frac{f(x_{0})}{f'(x_{0})} $

$ x_{0}-\frac{x_{0}^2-a}{2x_{0}} = \frac{1}{2}(x_{0}^2+\frac{a}{x_{0}}) $

Найдём точки пересечения параболы $ y=x^2-2$ с осью $ x$
$ x^{2}-2=0 $
$ x^{2}=2 $
$ x=\pm\sqrt{2} $

Проведём через точку $ x=1;y=-1 $ касательную к параболе
Производная функции $ y=x^{2}-2 $ равна $ 2x $
Значение функции в точке $ x_{0} = 1^2-2=-1 $
Подставим эти значения в формулу $ y = f'(x_{0})(x-x_{0})+f(x_{0}) $
Получим прямую $ y=2x-3 $, которая является касательной к параболе $ y=x^{2}-2 $ в точке $ (1;-1) $
Чтобы найти точку пересечения касательной с осью абсцисс приравняем к нулю левую часть уравнения $ y=2x-3 $
Отсюда $ x=3/2 $

Проведем касательную в точке $ x_{0} = 1.5 $
Получим прямую $ y = 3x-\frac{17}{4} $
которая пересекает ось абсцисс в точке $\frac{17}{12} $

Следующая касательная пересечёт ось абсцисс в точке $\frac{3462}{2448} $, и так далее…

В статье «Геометрический смысл производной» представлен метод построения касательной, основанный на определении длины подкасательной
Обозначим через $P$ проекцию точки касания $M$ на ось $OX$, а через $K$ — точку, в которой касательная пересекает ось $OX$. Из прямоугольного треугольника $KPM$ получаем: $ |KP|\cdot|tg\alpha|=|y| $
или, поскольку $ tg\alpha=y' $

$ |KP|=\frac{|y|}{|y'|} $





Используем данный метод для построения касательной к параболе $ y=x^2-2 $ в точке $ x=1; y=-1 $
Длина отрезка $ |KP|=\frac{|-1|}{|2|}=0.5 $, значит касательная пересекает ось абсцисс в точке $ x=1+0.5=1.5 $
Построим прямую, проходящую через точки $ x_{1}=1;y_{1}=-1 $ и $ x_{2}=1.5;y_{2}=0 $
$ k=f'(x_{0})=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=2 $
$ y-y_{0}=k(x-x_{0}) $
$ y+1=2(x-1) $
$ y=2x-3 $

#python
def f(x):
    f=x**2-2
    return f
def  Df(x):
    Df=2*x
    return Df
x=1
for i in range(10):
    x=x-f(x)/Df(x)
    print(x)



Метод Диофанта или метод секущих
Пусть примыкающие друг к другу отрезки $ a$ и $ b$ образуют диаметр полуокружности
Пускай $ a$ и $ b$ лежат в основании прямоугольных треугольников
Направим из точки примыкания луч перпендикулярно диаметру
Пускай на луче лежит высота $ h,$ высекаемая полуокружностью
В силу подобия прямоугольных треугольников $ h=\sqrt{ab} $


Пускай отрезок $ a$ и единичный отрезок $ b$ лежат на оси $ y$, отрезок $ h$ лежит на оси $ x$
Тогда полуокружность обращается в ноль в точке $\sqrt{a}$

Пусть дана окружность $ A: x^2+(y-\frac{n-1}{2})^2=(\frac{n+1}{2})^2 $, где $ n \in \mathbb{N} $
центр этой окружности лежит в точке $(0;\frac{n-1}{2})$
корни этой окружности лежат в точках $ (\pm \sqrt{n},0) $


Проведём прямую $ y=kx-1 $
Эта прямая, помимо точки $ (0;-1) $ встретит окружность $ A$ ещё в одной точке, координаты которой будут рациональными функциями от $ k $
$ x^2+(kx-1-\frac{n-1}{2})^2=(\frac{n+1}{2})^2 $
$ x^2+(kx-\frac{n+1}{2})^2=(\frac{n+1}{2})^2 $
$ x^2+k^2x^2+kx(n+1)=0 $
$ (k^2+1)x-k(n+1)=0 $

Таким образом, каждому рациональному значению $ k $ отвечает одна и только одна точка окружности $A$

Разделим $ (k^2+1)x-k(n+1)=0 $ на $ k(n+1)$:
$ \frac{k^2+1}{k(n+1)}x-1=0 $

Прямая $ B:y=\frac{k^2+1}{k(n+1)}x-1 $ пересечет ось абсцисс в точке $ x=\frac{k(n+1)}{k^2+1} $

Подставляя угловые коэффициенты $ k=\frac{k^2+1}{k(n+1)} $ в уравнение прямой $ B$ получим новые рациональные значения $k$ и новые точки окружности $A$, отвечающие этим значениям

#python
def approx(n):
    k=1
    for i in range(10):
        approx=(k*(n+1))/(k**2+1)
        print(approx)
        k=(k**2+1)/(k*(n+1))


Направим из точки $ B(\sqrt{2};0) $ вертикальный луч
Пускай этот луч встречает окружность $ x^2+y^2=(\frac{3}{2})^2 $ в точке $ C $
Соединим начало координат с точками $ B$ и $ C$ отрезками $AB $ и $ AC$

Тогда угол $ BAC=\arcsin=(\frac{BC}{AC})=\arcsin(\frac{1}{2}/\frac{3}{2})=\arcsin(\frac{1}{3}) \approx 0.339 $

$ \frac{180^{\circ} }{\pi} \cdot 0.399 \approx 19.47^{\circ} $



Косинус угла $ BAC=\frac{AB}{AC} \rightarrow \sqrt{2}=\frac{3}{2} \cdot \cos(\arcsin(\frac{1}{3})) $

Параметризация окружности
Проведём прямую под углом $ \alpha$ к оси абсцисс через точку $(-1,0)$
Пускай прямая высекает на окружности $ x^2+y^2=1 $ точку $ A$


по теореме Фалеса об угле, опирающемся на диаметр окружности $ \alpha+\beta=90^{\circ}$
Значит, угол наклона радиуса, проведённого к точке $ A$ из центра окружности равен $2\alpha$

Проведём прямую под тем же углом $ \alpha$ к оси абсцисс через начало координат
Пускай эта прямая высекает на прямой $ t$ точку $ t_{0}$

Тогда
$ tg(\alpha)=\frac{y}{1+x}=t $

$ tg(2\alpha)=\frac{y}{x}=\frac{2t}{1-t^2} $
Отсюда выражаются координаты точки $ A$, заданные в параметрической форме

$ x=\frac{1-t^2}{1+t^2} \:\:\:\: y=\frac{2t}{1+t^2} $



Пусть точка $ A$ лежит на окружности радиуса $ \sqrt{2}$
выражение для ординаты точки $ A$ заменится выражением

$ y=\frac{4t}{2+t^2}$


Подставляя в эту формулу рациональные значения $ t$ получим приближения к $ \sqrt{2}$


Метод половинного деления или метод бисекции

Метод основан на теореме Больцано-Коши о нуле непрерывной функции
Если функция непрерывна на некотором отрезке и на границах этого отрезка принимает значения противоположных знаков, то существует точка, в которой функция обращается в ноль



Пускай на выбранном отрезке функция $ y=f(x)$ возрастает и пускай точка $ a$ делит отрезок пополам

Если функция в точке $ a$ принимает положительное значение, значит она обращается в ноль слева от $ a$, если отрицательное — справа

Повторяя деления многократно, получим последовательность вложенных промежутков, пределом которой будет корень $ f(x)$, то есть число $ a $, такое что $ f(a)=0$

Определим функцию $ y=x^2-2 $ 
def y(x):
    return x*x-2

функция бисекции принимает границы интервала $ [a,b] $, а также количество итераций $ i $, вычисляет середину отрезка, определяет интервал, на котором функция $y=x^2-2 $ обращается в ноль, а затем рекурсивно вызывает саму себя с новыми параметрами 

def bisection(a, b, i):
    i=i-1 # уменьшаем количество итераций
    middle=(a+b)/2.0 # делим отрезок пополам
    print(middle)
    if i>0: 
        if(y(a)*y(middle)<0): # определяем нужный отрезок
            bisection(a,middle,i)
        if(y(middle)*y(b)<0):
            bisection(middle,b,i) #загружаем в функцию новые значения



Метод хорд
Пускай на границах промежутка $ (a,b) $ монотонная функция $ y=f(x)$ принимает значения разных знаков
Пускай прямая $ y=kx+b$ соединяет точки $ (x_{a},y_{a})$ и $ (x_{b},y_{b})$ и таким образом в точках $ x_{a}$ и $ x_{b}$ прямая $ y=kx+b$ принимает значения $ y_{a}$ и $ y_{b}$

Коэффициент $ k$ определяется соотношением

$ k=\frac{f(b)-f(a)}{b-a} $

Тогда $ b$ определяется соотношением

$ b=y-kx $

Добавлю, что значение неизвестных (переменных) величин $ k$ и $ b$ определяется системой уравнений



Пускай прямая $ y=kx+b$ обращается в ноль в точке $ a'$ и пускай уже на границах промежутка $ (a',b) $ монотонная функция $ y=f(x)$ принимает значения разных знаков
Соединим хордой точки $ (x',y')$ и $ (x_{b},y_{b})$, найдём точку $ a''$ пересечения хорды c осью $OX $
Повторяя приём многократно, найдём числа $ a, a',a'', \: ... $
Пределом данной последовательности будет корень $ f(x)=0$

следующий алгоритм переопределяет переменную $ approx$, вычисляя координаты точки пересечения прямой $ y=kx+b$ c отрезком $ AB$
#python
def f(x):
    f=x**2-2
    return f
def k(A,B):
    k=(f(B)-f(A))/(B-A)
    return k
def b(B,A):
    b=f(B)-k(A,B)*B
    return b
def a(A,B):
    a=-b(A,B)/k(A,B)
    return a
approx=a(1,2)
print(approx)
for i in range(10):
    approx=a(approx,2)
    print(approx)


Метод, представленный в журнале «Квант»⠀⠀

Следующий метод основан на лемме об охотнике и зайцах, которая гласит, что если луч $ l$ проходит через узел $A$ некоторой решётки, тогда найдётся такой узел, расстояние от которого до луча $l$ будет меньше любого наперёд заданного числа $\epsilon$
Это означает, что для любого иррационального числа $ \alpha>0$ и любого положительного $\epsilon $ найдутся такие натуральные $m$ и $n$, что $ |m\alpha-n|<\epsilon $

Проведём прямую $ y=\alpha x$, где $ \alpha=\sqrt{2} $
Прямая $ y=\alpha x$ пересекает каждую вертикальную прямую $ x=m $ в точке $ (m,m\alpha) $
Найдём на прямой $ x=m $ такую точку $n>m$, что $ \frac{(n-1)^2}{m^2}<2 $ и $ \frac{n^2}{m^2}>2 $

# python
for m in range(1,20):
	for n in range(m,20):
		if n**2/m**2>2:
			print('n / m=',n,'/',m)
			break




Методы Васильева
к задаче из сборника «Прямые и кривые»
Пусть лестница, стоящая на гладком полу, соскальзывает вниз
Пускай буквами $ A$ и $ B$ обозначаются точки соприкосновения лестницы со стеной и полом
Пускай эти точки лежат на координатных осях, точка $ C$ лежит в начале координат: таким образом вместе эти точки образуют прямоугольный треугольник $ ABC$

По мере соскальзывания длины катетов приближаются некому общему значению (длина большего катета приближается по избытку, длина меньшего — по недостатку): когда угол наклона лестницы к стене и полу составит $ 45^\circ $, треугольник $ ABC$ станет равнобедренным




Обозначим сравнявшиеся по длине катеты буквой $ n$
Пусть $ n \in \mathbb{N}$
По теореме Пифагора $ n^2+n^2=c^2$
отсюда $ c = \sqrt{2}n$
пусть для ясности $ n=1$, а значит требуется найти приближения к корню из двух

Пусть длина катета $ a$ увеличивается дискретно на величину $\delta=\frac{1}{10^k}$, иными словами $ a=\delta+\delta+\delta+...$
пускай $ k$ инкрементируется по достижении катетом $ a$ своего максимума, а приближение точки $ B$ к отметке $ \sqrt{2}$ своего минимума
получим последовательность отрезков
0.1
0.2
0.3
0.4
…

По теореме Пифагора получим приближения к квадрату $ \sqrt{2}$ из тождества $ b^2=c^2-a^2$

$ 2-(1.4)^2=0.04$
$ 2-(1.5)^2=-0.25$
значит $ max=1.4$
инкрементируем $ k$
$ 2-(1.41)^2=0.0119$
$ 2-(1.42)^2=-0.064$
значит $ max=1.41$
и так далее…

к задаче из журнала «Квант»
Пусть красными точками на прямой отмечены натуральные числа
Намотаем прямую на окружность длины $\sqrt{2} $, начав с точки $0 $
Ясно, что различные красные точки прямой перейдут при этом в различные точки окружности, поскольку равенство $k_{1}-k_{2}=n\sqrt{2} $ при целых $ n, \: k_{1} \ne k_{2} $ невозможно (ведь число $\sqrt{2} $ иррационально)


Метод прямого счёта позволяет определить, что за первые $ n $ оборотов $[n \cdot \sqrt{2}] $ красных точек «перейдут в различные точки окружности»

Пускай $ m$ равно количеству красных точек, оставляемых на $ n$ отрезках длины$ \sqrt{2}$
#python
m=0 # количество красных точек
n=0 # количество оборотов
while n<10:
    n=n+1 
    m=m+1 
    if (m+1)<n*2**0.5:
        m=m+1 
        print(m,"/",n)


Подставляя эти числа в уравнение $ m^2-2n^2=-1$ найдём последовательность наилучших приближений $\frac{m}{n} $ к корню из двух

Уравнения Пелля


Пусть натуральное число $ a $ не является квадратом. Легко видеть, что $ \sqrt{a} $ не выражается отношением натуральных чисел, т.е. не существует такой обыкновенной дроби $ \frac{x}{y} $, что $ (\frac{x}{y})^2=a $. Другими словами, если натуральное число $ a $ не является точным квадратом, то уравнение $ x^2-ay^2=0 $ не имеет решения в натуральных числах.
Попытаемся в этом случае выразить $ \sqrt{a} $ отношением натуральных чисел приближённо. Если $ \sqrt{a} \approx \frac{x}{y} $, то $ x^2-ay^2 \approx 0 $. Самое близкое к нулю натуральное число — это единица. Поэтому дело сводится к решению в натуральных числах диофантова уравнения

$ x^2-ay^2=1 $


которое носит название… уравнения Пелля

Уточню, что $\sqrt{N}$ является иррациональным, если $ N $ не является точным квадратом
Доказательство иррациональности $\sqrt{N}$ («Квант» 1974)
Пусть дано число $ N $, и $ \sqrt{N}=\frac{p}{q} $, где $ p $ и $ q $ — натуральные числа.
Пусть дробь $ \frac{p}{q} $ — несократимая (ведь любую дробь можно сокращать, пока у числителя и знаменателя не сократятся все общие делители).
Тогда $ \frac{p^2}{q^2}=N. $
В левой части стоит несократимая дробь (ведь $ p $ и $ q $ не имеют общих делителей), а в правой части уравнения — заведомо целое число. Но дробное число не может быть равно целому.
Значит,… число $\sqrt{N}$ не является рациональным, откуда следует, что оно иррациональное, что и требовалось доказать.


Пусть дано уравнение $ x^{2}-2y^{2} = \pm 1 $

Подбором найдём несколько решений $ (x;y)=(1;0),(1;1) $ или $ (3;2) $

Здесь каждая новая пара выражается через предыдущую подстановкой в рекуррентную формулу
$ y_{n+1} = x_{n}+y_{n} $
$ x_{n+1} = y_{n+1}+y_{n}=x_{n}+y_{n}+y_{n}=x_{n}+2 \cdot y_{n} $ 

x0=1
y0=1
x=0 
y=0 
i=0
while i<=6:
    y=x0+y0
    x=2*y0+x0
    x0=x
    y0=y
    i=i+1 
print(x)
print(y)

Получившиеся приближение $ \frac{577}{408} $ было известно ещё математикам древней Индии


Корни квадратичной функции



Пусть функция $ P(x) $ определена полиноминальным уравнением степени $ n$
Полином $ n- $ой степени от переменной $ x $ есть сумма вида $ P(x)=c_{0}+c_{1}x+c_{2}x^2+c_{3}^3+...+c_{n}x^{n} $

Точки пересечения квадратичной функции с осью абсцисс определяются выражением $ 0=c_{0}+c_{1}x^1+c_{2}x^2 $

Пускай число $ a$ является корнем $ P(x)$
Говорят, что $ P(x)$ делится на $ Q(x) $, если справедливо тождество $ P(x)=(x-a)\cdot Q(x)$

Теорема Безу гласит, что

остаток $ r $ от деления $ P(x) $ на $ (x-a) $ равен $ P(a) $

Пусть $ P(x)=Q(x)(x-a)+r $
Тогда $ P(a)=Q(a)(a-a)+r=r $
Из этого равенства мы видим, что $ r$ равно нулю, если $ P(a)$ равно нулю, то есть если число $ a$ — корень $ P(x)$

Определим экстремум функции $ f(x)=x^2+px+q$ согласно лемме Ферма
$ f(x)'=0 $
$ x=-p/2 $

Дискриминант определяется подстановкой $ x=-p/2$ в функцию $ P(x)=x^2+px+q $
$ P(-\frac{p}{2})=\frac{p^2}{4}-p\frac{p}{2}+q=-\frac{p^2}{4}+q=-\frac{p^2-4q}{4}=-\frac{D}{4} $

Поскольку $ (x^2+px+q) / (x+\frac{p}{2})=(x+\frac{p}{2})+r, $ где остаток $ r = -\frac{D}{4}$

Отсюда $ (x+\frac{p}{2})^2=\frac{1}{4}(p^2-4q) $
Путём понижения степени придём к выражению
$ x_{1,2}+\frac{p}{2}=\pm \frac{\sqrt{D}}{2} $ отсюда $ x_{1,2}=-\frac{p}{2} \pm \frac{\sqrt{D}}{2} $


Подставим $ \frac{1}{2} $ в функцию $ f(x)=x^2-x-1 \rightarrow f(\frac{1}{2})=\frac{1}{4}-\frac{1}{2}-1=-\frac{5}{4} $
Тогда
$ (x-\frac{1}{2})^2-\frac{5}{4}=0 $
$ (x-\frac{1}{2})^2 = \frac{5}{4} $
$ x-\frac{1}{2}= \frac{\sqrt{5}}{2} $
$ x=\frac{\sqrt{5}+1}{2} $

Теорема Виета гласит, что
сумма корней приведённого квадратного уравнения равна второму коэффициенту с противоположным знаком, а их произведение равно свободному коэффициенту

$ x_{1}+x_{2} = -p $
$ x_{1} \cdot x_{2} = q $

Метод резольвент

Сумма и произведение корней уравнения $ x^2-x-1=0 $ равны
$ x_{1}+x_{2}=1 $
$ x_{1}x_{2}=-1 $

коэффициенты $p $ и $q $ связаны соотношением
$ (x_{1}-x_{2})^2=x_{1}^2-2x_{1}x_{2}+x_{2}^2=$
$=x_{1}^2+2x_{1}x_{2}+x_{2}^2-4x_{1}x_{2}= (x_{1}+x_{2})^2-4x_{1}x_{2} $
Подставив числовые значения в уравнение, получим
$ (x_{1}+x_{2})^2-4x_{1}x_{2}= 1-4(-1)=5 $
Значит
$ (x_{1}-x_{2})^2=5 $
$ x_{1}-x_{2}= \sqrt{5} $
Тогда
$ x_{1}-x_{2}= \sqrt{5} $
$ x_{1}+x_{2}=1 $
а значит число $ \phi $ равно
$ 2x_{1}= \sqrt{5}+1 \rightarrow x_{1}=\frac{\sqrt{5}+1}{2} $

Подробнее об этом методе решения здесь



Метод Лобачевского позволяет найти приближённое значение одного из корней
Пусть
$ P(x)P(-x)=(x-x_{1})(x-x_{2})(x+x_{1})(x+x_{2})=(x^2-x_{1}^2)(x^2-x_{2}^2) $

$ P(x)P(-x)=(x^2+px+q)(x^2-px+q)=x^4-(p^2-2q)x^2+q^2 $

Произведём замену $ t=x^2 $
$ Q(t)=(t-t_{1})(t-t_{2}) $
$ Q(t)=t^2-(p^2-2q)t+q^2 $

Таким образом корни исходного уравнения «возводятся в квадрат»
По теореме Виета сумма «возведённых» корней будет равна $ (p^2-2q) $

Если повторить этот приём многократно, корни «возведутся» в четвёртую, восьмую, шестнадцатую и т.д. степень
Один из корней станет пренебрежимо мал по сравнению с другим, тогда оставшийся корень станет приближённо равен абсолютному значению второго коэффициента квадратного уравнения $ P(x)=x^2+px+q $, возведённого в некую высшую степень

Коэффициенты этого уравнения связаны с коэффициентами уравнений низших степеней величинами $ (p^2-2q) $ и $ q^2 $
$ p_{n}=p_{n-1}^2-2q_{n-1} $
$ q_{n}=q_{n-1}^2 $

Пусть $p=-1$ и $ q=-1 $
Тогда $ t^2-3t+1=0 $
По теореме Виета $ t_{1}+t_{2}=3 $
а значит $ x^2 \approx 3 $
$ x^4 \approx 3^2-2=7 $
$ x^8 \approx 7^2-2=47 $
$ x^{16} \approx 47^2-2=2207 $
$ x^{32} \approx 2207^2-2=4870847 $

найдём значение $ x $ по формуле
$ x=\frac{a+(k-1)x^k}{kx^{k-1}} $

#python
a=4870847
x=2
for i in range(10):
    x=(a+31*x**32)/(32*x**31)
print(x)



Лемма Ферма утверждает, что производная дифференцируемой функции в точке экстремума равна нулю
Её касательная в данной точке параллельна оси абсцисс
Для нахождения экстремумов многочлена $ F(x)$ Ферма предлагает следующее правило:
1) подставляем в $ F(x)$ вместо $ x$ выражение $ x+h $;
2) приравниваем $ F(x)$ и $ F(x+h): \: F(x)=F(x+h)$;
3) после приведения подобных членов сокращаем на $ h$;
4) полагаем $ h=0$.
В результате получаем равенство $ A(x)=0$. Ферма утверждает, что все значения $ x$, при которых многочлен $ F(x)$ имеет экстремум, необходимо являются корнями уравнения $ A(x)=0.$ Сама функция $ A(x) $, которая по правилу Ферма получается чисто алгебраически (т.е. без предельного перехода), теперь называется производной от $ F(x)$.

Следуя данному правилу, найдём экстремум функции $ f(x)=x^2-x-1 $
$ (x+h)^2-(x+h)-1=x^2-x-1 $
$ x^2+2xh+h^2-x-h-1=x^2-x-1| \: :h $
$ 2x+h-1=0 $
$ h=0 $
$ x=\frac{1}{2} $

Согласно теореме Ролля экстремум функции $ y=f(x)$ лежит между точками $ a$ и $ b$, такими что $ f(a)=f(b)$
Пусть точка $ a$ лежит на оси ординат, то есть $ a_{x}=0; a_{y}=f(0)$
Проведём через точку $ a$ горизонтальную прямую
Пускай эта прямая встречает параболу в точке $ b$
Точки $ a$ и $ b$ высекут на этой прямой отрезок
Ось параболы разделит отрезок $ (a,b) $ пополам

Пусть дана парабола $ y=x^2-x $
Будем сдвигать параболу вертикально вниз до тех пор, пока произведение корней не превысит некий порог, который по теореме Виета равен $ \phi\cdot (-\frac{1}{\phi}) $


Пускай расстояние между корнями изменяется дискретно
определим переменную step, равную данной дискретной величине

def foo(x1,x2,step):
    x1=x1+step // прибавляем шаг
    x2=x2+step
    if x1*x2<1:
        foo(x1,x2,step)
    else:
        print(x2-step)
        #декремент шага      
foo(0,1,0.1)

Пускай «длина шага» уменьшается на порядок перед тем, как произведение корней покинет интервал $ [0;-1) $

    else:
        print(x2-step)
        #декремент шага
        x1=x1-step
        x2=x2-step
        step=step/10 #уменьшаем размер шага на порядок
        foo(x1,x2,step)

При длине шага $ 0.1$ число $ \phi \approx 1.6 $
уменьшаем размер шага на порядок
$ \phi \approx 1.61 $
ещё на порядок
$ \phi \approx 1.618 $
и так далее…


Согласно Лагранжу, первые основы динамики были заложены Галилеем
Полученная Галилео Галилеем формула $ s=\frac{at^2}{2} $ определяет квадратичную зависимость расстояния от времени при равноускоренном/равнозамедленном движении материальной точки вдоль координатной оси

Пускай начальная координата материальной точки $ x_{0}=-1,$ начальная скорость $ v_{0}=-1,$ ускорение $ a=2$
Отрицательная величина скорости означает, что в начальный момент времени материальная точка движется противоположно направлению координатной оси
Такое движение определяется уравнением $ s=-1-t+t^2$
за время $ t_{1}=\frac{1}{2}$ материальная точка замедляется до полной остановки, затем ускоряется и проходит путь $ s=\frac{5}{4}$ за время $ t_{2}=\frac{\sqrt{5}}{2} $
Тогда общее время в пути до момента встречи с осью абсцисс составляет $ t_{1}+t_{2}=\frac{1}{2}+\frac{\sqrt{5}}{2}= \frac{1+\sqrt{5}}{2} $

P.S.
Следующая задача из сборника Арнольда рассматривается в статье журнала «Квант» Удивительные приключения периодических дробей

27. Доказать, что остаток от деления числа $ 2^{p-1} $ на простое нечетное число
$ p $ равен $ 1 $
(примеры: $ 2^{2} = 3a+1, 2^{4}=5b+1, 2^{6}=7c+1, 2^{10} -1 = 1023 = 10 \cdot 93) $.

P.P.S. Статья о цепных дробях «Об одной задаче, которую больше не предлагают на собеседовании» ссылка

Книги


Задачи для детей от 5 до 15 лет В. И. Арнольд
Курс дифференциального и интегрального исчисления Г. М. Фихтенгольц
Теория чисел А. А. Бухштаб
За страницами учебника математики Н. Я. Виленкин, Л. П. Шибасов, З. Ф. Шибасова
Алгебра Н. Я. Виленкин, Р. С. Гутер, С. И. Шварцбурд
Что такое производная Н. Я. Виленкин, А. Г. Мордкович, журнал «Квант»
Диофант и диофантовы уравнения И.Г. Башмакова
Пьер Ферма И.Г. Башмакова, журнал «Квант»
Диофантовы уравнения и рациональные точки М.И. Башмаков, журнал «Квант»
Геометрический смысл производной А.Я. Хинчин, журнал «Квант»
Занимательная геометрия Я.И. Перельман
Метод математической индукции И.С. Соминский
Число Фидия — золотое сечение А.П. Савин, журнал «Квант»
Числа Фибоначчи Н. Н. Воробьёв
Числа Фибоначчи А. Спивак, журнал «Квант»
Уравнения Пелля В. Сендеров, А. Спивак, журнал «Квант»
Золотое сечение А. Д. Бендукидзе, журнал «Квант»
Решётки и правильные многоугольники А. Егоров, журнал «Квант»
Числа и многочлены С. Ашманов, журнал «Квант»
Сколько корней у многочлена? С. Табачников, журнал «Квант»
Уравнения, которые удается решить А. Тоом, журнал «Квант»
Формулы Виета Ц.С. Копрински, журнал «Квант»
История о том, как Галилей открыл законы движения С. Гиндикин, журнал «Квант»
Метод Лобачевского А.Л. Брудно, журнал «Квант»
Прямые и кривые Н.Б. Васильев, В.Л. Гутенмахер
Пределы, непрерывность Н.Я. Виленкин, А.Г. Мордкович
Пределы А.А. Кириллов
Что такое математика? В.И. Арнольд
Что такое математика? Курант Р., Роббинс Г.
Digital Arithmetic Ercegovac Milos D., Lang Tomas
О книге с большой буквы А. Щетников, журнал «Квантик»
Tags:
Hubs:
Total votes 24: ↑18 and ↓6+12
Comments26
19
Karma
0
Rating
Дмитрий @demsp

User

Send message

Articles

Your account

Sections

Information

Services

Support
© 2006–2025, Habr