Привет всем! Хочу поделиться с Вами своей идеей машинного обучения.
Большие достижения в области машинного обучения, впечатляют. Сверточные сети и LSTM это круто. Но почти все современные технологии основаны на обратном распространении ошибки. На основе этого метода вряд ли получится построить думающую машину. Нейронные сети получаются чем-то вроде замороженного мозга, обученного раз и навсегда, неспособнымменяться размышлять.
Я подумал, почему бы не попробовать создать что-то похожее на живой мозг. Этакий реинжиниринг. Поскольку у всех животных, несмотря на различия в интеллекте, мозг состоит из примерно одинаковых нейронов, в основе его работы должен лежать какой-то базовый принцип.
Есть несколько вопросов, на которые я не нашел однозначных ответов в популярной литературе;
Правдоподобным ответом на все эти вопросы мне представляется то, что мозг работает как множество простых кластеризаторов. Можно ли выполнить такой алгоритм на группе нейронов? Например метод К-средних. Вполне, только нужно его немного упростить. В классическом алгоритме центры вычисляются итеративно как среднее всех рассмотренных примеров, но мы будем смещать центр сразу после каждого примера.
Посмотрим, что нам нужно, чтобы реализовать алгоритм кластеризации.
Проверим получившийся алгоритм на практике. Я набросал несколько строчек на Питоне. Вот что получается с двумя измерениями из случайных чисел:

А вот MNIST:

На первый взгляд, кажется что все вышеописанное ничего не изменило. Ну были у нас на входе одни данные, мы их как-то преобразовали, получили другие данные.
Но на самом деле есть разница. Если до преобразования мы имели кучу аналоговых параметров, то после преобразования имеем только один параметр, при этом закодированный унитарным кодом. Каждому нейрону в группе можно сопоставить определенное действие.
Приведу пример: Допустим в группе кластеризаторе есть только два нейрона. Назовем их “ВКУСНО” и “СТРАШНО”. Чтобы позволить мозгу принимать решение, нужно только к первому подсоединить нейрон “КУШАТЬ”, а ко второму “УБЕГАТЬ”. Для этого нам нужен учитель. Но сейчас не об этом, обучение с учителем тема для другой статьи.
Если увеличивать количество кластеров, то точность будет постепенно расти. Крайний случай — количество кластеров равное количеству примеров. Но есть проблема, количество нейронов в мозге ограничено. Нужно постоянно идти на компромисс, либо точность либо размер мозга.
Предположим, что у нас есть не одна группа-кластеризатор, а две. При этом на входы подаются одинаковые значения. Очевидно, что получится одинаковый результат.
Давайте внесем небольшую случайную ошибку. Пусть, иногда, каждый кластеризатор выбирает не самый близкий центр кластера, а какой попало. Тогда значения начнут различаться, со временем разница будет накапливаться.

А теперь, подсчитаем ошибку у каждого кластеризатора. Ошибка это разница между входным примером и центром выбранного кластера. Если один кластеризатор выбрал ближайшее значение, а другой случайное, то ошибка у второго будет больше.
Идем дальше, добавим на вход каждого кластеризатора маску. Маска это набор коэффициентов для каждого входа. Не ноль или единица, как обычно используется в масках, а некоторое вещественное число от нуля до единицы.
Перед тем как подать пример на вход кластеризатора будем умножать этот пример на маску. Например, если маска используется для картинки, то если для какого-то пикселя маска равна единице, то она как бы совершенно прозрачна. А если маска равна нулю, то этот пиксель всегда черный. А если маска равна 1/2, то пиксель затемнен наполовину.
А теперь главное действие, будем уменьшать значение маски пропорционально ошибке кластеризатора. То есть, если ошибка большая, то уменьшим значение сильнее, а если нулевая то не будем уменьшать совсем.
Для того, чтобы значения масок постепенно не обнулились, будем их нормировать. То есть, сумма значений масок для каждого входного параметра, всегда равна единица. Если в одной маске что-то отнимается, то к другой это прибавляется.
Попробуем посмотреть, что получается на примере MNIST. Видим что маски постепенно разделяют пиксели на две части.
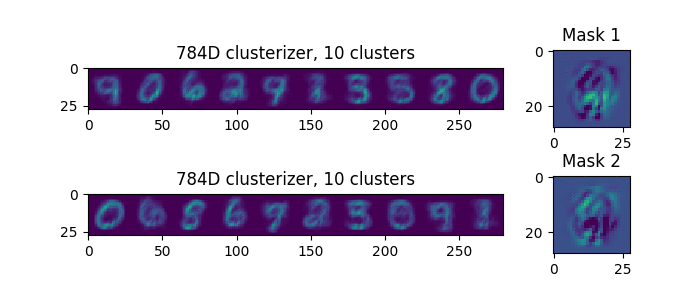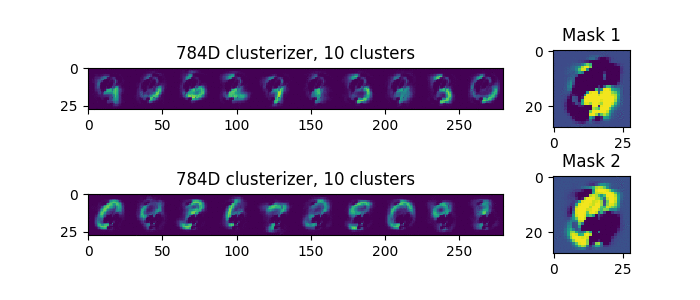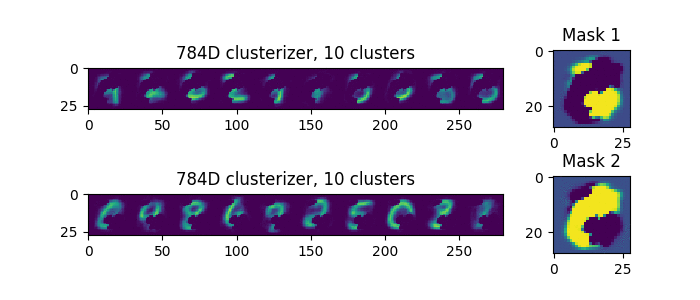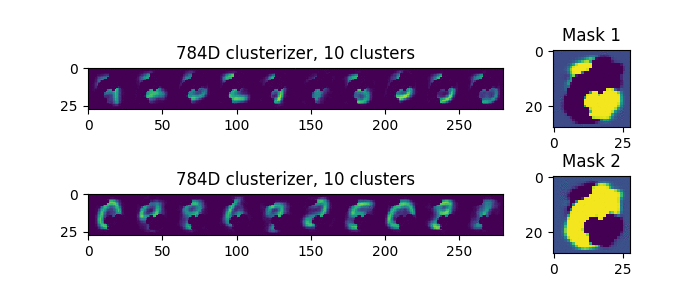
В правой части картинки показаны получившиеся маски. По окончании процесса, верхний кластеризатор рассматривает правую нижнюю часть, а нижний кластеризатор оставшуюся часть подаваемых примеров. Интересно, что если мы запустим процесс повторно, то получим другое разделение. Но при этом группы параметров получаются не как попало, а таким образом, чтобы снизить ошибку предсказания. Кластеризаторы как бы примеряют каждый пиксель к своей маске, и при этом пиксель забирает тот кластеризатор, которому пиксель подходит лучше.
Попробуем подавать на вход сдвоенные цифры, не наложенные друг на друга, а расположенные рядом, вот такие (это один пример, а не два):

Теперь мы видим, что каждый раз, разделение происходит одинаково. То есть, если есть единственный, явно лучший вариант разделения масок, то он и будет выбран.

Случайным будет только одно, выберет ли первая маска левую цифру или правую.
Я называю полученные маски мета-кластерами. А процесс формирования масок мета-кластеризацией. Почему мета? Потому, что происходит кластеризация не входных примеров, а самих входов.
Пример посложнее. Попробуем разделить 25 параметров на 5 мета-кластеров.
Для этого возьмем пять групп по пять параметров, закодированные унитарным кодом.
То есть в каждой группе одна и только одна единица на случайном месте. В каждом подаваемом примере всегда пять единиц.
На картинках ниже каждый столбец это входной параметр, а каждая строка это маска мета-кластера. Сами кластеры не показаны.

100 параметров и 10 мета-кластеров:
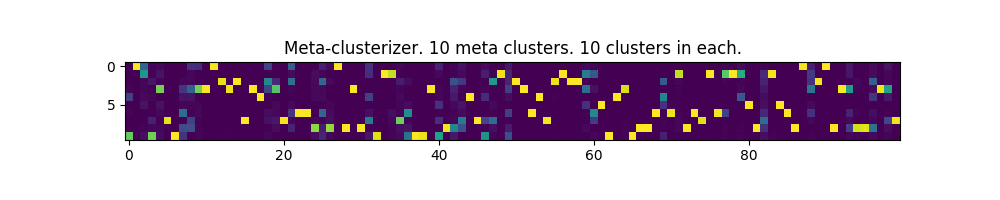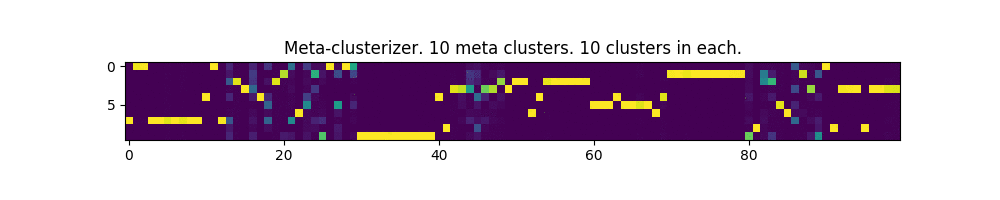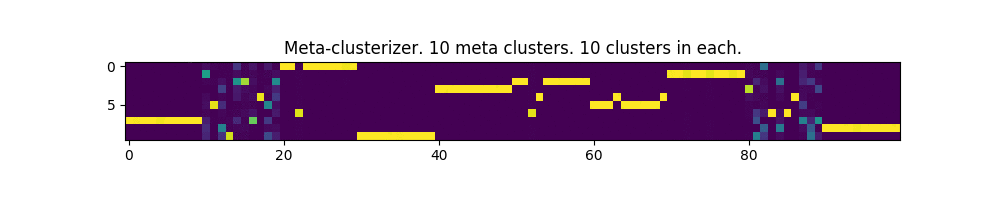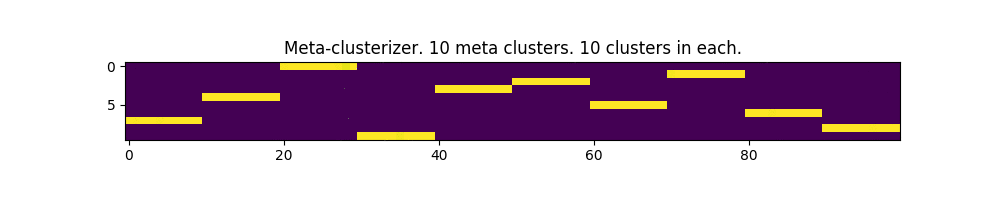
Работает! Местами, даже немного напоминает изображение матрицы из одноименного фильма.
Применяя мета-кластеризацию можно радикально снизить количество кластеров.
Например, возьмем десять групп по десять параметров, в каждой группе одна единица.
Если у нас один кластеризатор (нет мета-кластеров), то нам нужно 1010 = 10000000000 кластеров, чтобы получить нулевую ошибку.
А если у нас десять кластеризаторов, то нужно всего 10 * 10 = 100 кластеров. Это похоже на десятичную систему счисления, не нужно придумывать обозначения для всех возможных чисел, можно обойтись десятью цифрами.
Мета-кластеризация очень хорошо распараллеливается. Самые затратные вычисления (сравнение примера с центром кластера) можно выполнять независимо для каждого кластера. Обратите внимание, не для кластеризатора, а для кластера.
До этого я говорил только о дендритах, но у нейронов есть аксоны. Причем они тоже учатся. Так вот, очень похоже, что аксоны это и есть маски мета-кластеров.
Добавим к описанию работы дендритов, приведенному выше, еще одну функцию.
Предположим, что если происходит спайк нейрона, все дендриты как-то выбрасывают в синапс какое-то вещество, показывающее концентрацию нейромедиатора в дендрите. Не из аксона в дендрит, а обратно. Концентрация этого вещества зависит от ошибки сравнения. Пусть, чем ошибка меньше, тем большее количество вещества выбрасывается. Ну и аксон реагирует на количество этого вещества и растет. А если вещества мало, что означает большую ошибку, то аксон постепенно уменьшается.
И если так изменять аксоны с самого рождения мозга, то со временем, они будут идти только к тем группам нейронов где их спайки этих аксонов нужны (не приводят к большим ошибкам).
Пример: пусть нужно запоминать человеческие лица. Пусть каждое лицо изображено с помощью мегапиксельного изображения. Тогда для каждого лица нужен нейрон с миллионом дендритов, что нереально. А теперь разделим все пиксели на мета-кластеры, такие как глаза, нос, уши и так далее. Всего десять таких мета-кластеров. Пусть в каждом мета-кластере будет десять кластеров, десять вариантов носа, десять вариантов ушей и так для всего. Теперь, чтобы запомнить лицо, достаточно нейрона с десятью дендритами. Это снижает объем памяти (ну и объем мозга) на пять порядков.
А теперь, если допустить, что мозг состоит из мета-кластеров, можно попытаться рассмотреть с этой точки зрения некоторые понятия, присущие живому мозгу:
Кластеры необходимо постоянно обучать, иначе новые данные, не будут правильно обрабатываться. Для обучения кластеров в мозге нужна сбалансированная выборка. Поясню, если сейчас зима, то мозг будет учится только на зимних примерах, и полученные кластеры постепенно станут релевантными только зиме, а летом у этого мозга все будет плохо. Что с этим делать? Нужно периодически на все кластеризаторы подавать не только новые, но и старые важные примеры (воспоминания и зимы и лета). И чтобы этим воспоминаниям не мешали текущие ощущения, нужно органы чувств временно отключить. У животных это называется сон.
Представьте, мозг видит что-то маленькое, СЕРЕНЬКОЕ, которое бежит. После мета-кластеризации имеем три активных нейрона в трех мета-кластерах. И благодаря воспоминанию, мозг знает, что это вкусно. Потом, мозг видит что-то маленькое, СИНЕНЬКОЕ, которое бежит. Но мозг не знает, вкусно это или страшно. Достаточно временно отключить мета-кластер, где находятся цвета, и останется только маленькое, которое бежит. А мозг знает это это вкусно. Это называется аналогия.
Допустим, мозг вспомнил что-то, а потом, изменил активный нейрон-кластер в какой-то группе на любой другой, при этом в остальных мета-кластерах остается реальное воспоминание. И вот, мозг уже представил что-то такое, что никогда раньше не видел. А это уже воображение.
Спасибо за внимание, код здесь.
Большие достижения в области машинного обучения, впечатляют. Сверточные сети и LSTM это круто. Но почти все современные технологии основаны на обратном распространении ошибки. На основе этого метода вряд ли получится построить думающую машину. Нейронные сети получаются чем-то вроде замороженного мозга, обученного раз и навсегда, неспособным
Я подумал, почему бы не попробовать создать что-то похожее на живой мозг. Этакий реинжиниринг. Поскольку у всех животных, несмотря на различия в интеллекте, мозг состоит из примерно одинаковых нейронов, в основе его работы должен лежать какой-то базовый принцип.
Что я не знаю о нейронах
Есть несколько вопросов, на которые я не нашел однозначных ответов в популярной литературе;
- Очевидно, нейрон как-то реагирует на нейромедиаторы, но как именно? Простое предположение, что чем больше нейромедиатора тем чаще спайки, очевидно не выдерживает никакой критики. Если бы было так, то срабатывание одного нейрона вызывало бы срабатывание нескольких соседей, те следующих, и через короткое время эта лавина захватила бы весь мозг. Но на самом деле этого не происходит, одновременно в мозге работает только небольшая часть нейронов. Почему?
- Очевидно, что нейроны являются единицами памяти, но как они хранят информацию? Центральная часть нейрона не представляет собой ничего особенного: ядро митохондрии и тому подобное. Аксон на спайк влиять не может, поскольку информация идет только в одну сторону, от ядра. Значит единственное что остается это дендриты. Но как в них хранится информация? В аналоговой или цифровой форме?
- Очевидно, что нейроны как-то обучаются. Но как именно? Допустим, что дендриты растут в тех местах, где нейромедиатора было много непосредственно перед спайком. Но если это так, то сработавший нейрон немножко вырастет и в следующий раз когда появится нейромедиатор он будет самый толстый среди соседей, впитает больше всех нейромедиатора и снова сработает. И снова немножко подрастет. И так до бесконечности, пока не задушит всех своих соседей? Что-то тут не так?
- Если один нейрон растет, то соседние должны уменьшатся, голова-то не резиновая. Что-то должно побуждать нейрон усыхать. Что?
Просто кластеризация
Правдоподобным ответом на все эти вопросы мне представляется то, что мозг работает как множество простых кластеризаторов. Можно ли выполнить такой алгоритм на группе нейронов? Например метод К-средних. Вполне, только нужно его немного упростить. В классическом алгоритме центры вычисляются итеративно как среднее всех рассмотренных примеров, но мы будем смещать центр сразу после каждого примера.
Посмотрим, что нам нужно, чтобы реализовать алгоритм кластеризации.
- Центры кластеров, конечно же это дендриты нейронов нашей группы. Но как запомнить информацию? Предположим, что элементарной ячейкой хранения информации в дендрите является объем веточки дендрита в области синапса. Чем веточка толще, соответственно больше её объем, тем большее значение сохранена. Таким образом каждый дендрит может запомнить несколько аналоговых величин.
- Компараторы, позволяющие вычислить близость примера. Тут посложнее. Предположим, что после подачи данных (аксоны выбросили нейромедиатор) каждый нейрон сработает тем быстрее, чем более сохраненные данные (центр кластера) похожи на поданный пример (количество нейромедиаторов). Обратите внимание, на скорость срабатывания нейрона влияет не абсолютное количество нейромедиатора, а именно близость количества нейромедиатора к сохраненным в дендритах значению. Предположим, что если нейромедиатора мало, то дендрит не дает команду на спайк. Ничего не происходит и если нейромедиатора много, спайк дендритной веточки происходит раньше чем у других дендритной веточек и не доходит до ядра. А вот если нейромедиатора в самый раз, тогда все дендритные веточки дадут мини-спайк примерно одновременно, и эта волна превратится в спайк нейрона, который пойдет по аксону.
- Многовходовый компаратор позволяет сравнить результаты и выбрать лучший. Предположим, что находящиеся рядом нейроны обладают тормозящим действием на всех своих соседей. Так, в некоторой группе нейронов, активным в каждый момент времени может являться только один. Именно тот, который сработал первым. Поскольку нейроны в группе находятся рядом, они имеют одинаковый доступ ко всем аксонам приходящим к этой группе. Таким образом в группе сработает тот нейрон, у которого запомненная информация наиболее близка к рассматриваемому примеру.
- Механизм смещения центра в сторону примера. Ну тут все просто. После спайка нейрона, все дендриты этого нейрона меняют свой объем. Там где концентрация нейромедиатора была слишком большой, веточки растут. Там где была недостаточной, веточки уменьшаются. Там где концентрация в самый раз, объем не меняется. Объемы веточек меняются по чуть-чуть. Но сразу. Следующий спайк — следующее изменение.
Проверим получившийся алгоритм на практике. Я набросал несколько строчек на Питоне. Вот что получается с двумя измерениями из случайных чисел:

А вот MNIST:

На первый взгляд, кажется что все вышеописанное ничего не изменило. Ну были у нас на входе одни данные, мы их как-то преобразовали, получили другие данные.
Но на самом деле есть разница. Если до преобразования мы имели кучу аналоговых параметров, то после преобразования имеем только один параметр, при этом закодированный унитарным кодом. Каждому нейрону в группе можно сопоставить определенное действие.
Приведу пример: Допустим в группе кластеризаторе есть только два нейрона. Назовем их “ВКУСНО” и “СТРАШНО”. Чтобы позволить мозгу принимать решение, нужно только к первому подсоединить нейрон “КУШАТЬ”, а ко второму “УБЕГАТЬ”. Для этого нам нужен учитель. Но сейчас не об этом, обучение с учителем тема для другой статьи.
Если увеличивать количество кластеров, то точность будет постепенно расти. Крайний случай — количество кластеров равное количеству примеров. Но есть проблема, количество нейронов в мозге ограничено. Нужно постоянно идти на компромисс, либо точность либо размер мозга.
Мета-кластеризация
Предположим, что у нас есть не одна группа-кластеризатор, а две. При этом на входы подаются одинаковые значения. Очевидно, что получится одинаковый результат.
Давайте внесем небольшую случайную ошибку. Пусть, иногда, каждый кластеризатор выбирает не самый близкий центр кластера, а какой попало. Тогда значения начнут различаться, со временем разница будет накапливаться.

А теперь, подсчитаем ошибку у каждого кластеризатора. Ошибка это разница между входным примером и центром выбранного кластера. Если один кластеризатор выбрал ближайшее значение, а другой случайное, то ошибка у второго будет больше.
Идем дальше, добавим на вход каждого кластеризатора маску. Маска это набор коэффициентов для каждого входа. Не ноль или единица, как обычно используется в масках, а некоторое вещественное число от нуля до единицы.
Перед тем как подать пример на вход кластеризатора будем умножать этот пример на маску. Например, если маска используется для картинки, то если для какого-то пикселя маска равна единице, то она как бы совершенно прозрачна. А если маска равна нулю, то этот пиксель всегда черный. А если маска равна 1/2, то пиксель затемнен наполовину.
А теперь главное действие, будем уменьшать значение маски пропорционально ошибке кластеризатора. То есть, если ошибка большая, то уменьшим значение сильнее, а если нулевая то не будем уменьшать совсем.
Для того, чтобы значения масок постепенно не обнулились, будем их нормировать. То есть, сумма значений масок для каждого входного параметра, всегда равна единица. Если в одной маске что-то отнимается, то к другой это прибавляется.
Попробуем посмотреть, что получается на примере MNIST. Видим что маски постепенно разделяют пиксели на две части.

В правой части картинки показаны получившиеся маски. По окончании процесса, верхний кластеризатор рассматривает правую нижнюю часть, а нижний кластеризатор оставшуюся часть подаваемых примеров. Интересно, что если мы запустим процесс повторно, то получим другое разделение. Но при этом группы параметров получаются не как попало, а таким образом, чтобы снизить ошибку предсказания. Кластеризаторы как бы примеряют каждый пиксель к своей маске, и при этом пиксель забирает тот кластеризатор, которому пиксель подходит лучше.
Попробуем подавать на вход сдвоенные цифры, не наложенные друг на друга, а расположенные рядом, вот такие (это один пример, а не два):

Теперь мы видим, что каждый раз, разделение происходит одинаково. То есть, если есть единственный, явно лучший вариант разделения масок, то он и будет выбран.

Случайным будет только одно, выберет ли первая маска левую цифру или правую.
Я называю полученные маски мета-кластерами. А процесс формирования масок мета-кластеризацией. Почему мета? Потому, что происходит кластеризация не входных примеров, а самих входов.
Пример посложнее. Попробуем разделить 25 параметров на 5 мета-кластеров.
Для этого возьмем пять групп по пять параметров, закодированные унитарным кодом.
То есть в каждой группе одна и только одна единица на случайном месте. В каждом подаваемом примере всегда пять единиц.
На картинках ниже каждый столбец это входной параметр, а каждая строка это маска мета-кластера. Сами кластеры не показаны.

100 параметров и 10 мета-кластеров:

Работает! Местами, даже немного напоминает изображение матрицы из одноименного фильма.
Применяя мета-кластеризацию можно радикально снизить количество кластеров.
Например, возьмем десять групп по десять параметров, в каждой группе одна единица.
Если у нас один кластеризатор (нет мета-кластеров), то нам нужно 1010 = 10000000000 кластеров, чтобы получить нулевую ошибку.
А если у нас десять кластеризаторов, то нужно всего 10 * 10 = 100 кластеров. Это похоже на десятичную систему счисления, не нужно придумывать обозначения для всех возможных чисел, можно обойтись десятью цифрами.
Мета-кластеризация очень хорошо распараллеливается. Самые затратные вычисления (сравнение примера с центром кластера) можно выполнять независимо для каждого кластера. Обратите внимание, не для кластеризатора, а для кластера.
Как это работает в мозге
До этого я говорил только о дендритах, но у нейронов есть аксоны. Причем они тоже учатся. Так вот, очень похоже, что аксоны это и есть маски мета-кластеров.
Добавим к описанию работы дендритов, приведенному выше, еще одну функцию.
Предположим, что если происходит спайк нейрона, все дендриты как-то выбрасывают в синапс какое-то вещество, показывающее концентрацию нейромедиатора в дендрите. Не из аксона в дендрит, а обратно. Концентрация этого вещества зависит от ошибки сравнения. Пусть, чем ошибка меньше, тем большее количество вещества выбрасывается. Ну и аксон реагирует на количество этого вещества и растет. А если вещества мало, что означает большую ошибку, то аксон постепенно уменьшается.
И если так изменять аксоны с самого рождения мозга, то со временем, они будут идти только к тем группам нейронов где их спайки этих аксонов нужны (не приводят к большим ошибкам).
Пример: пусть нужно запоминать человеческие лица. Пусть каждое лицо изображено с помощью мегапиксельного изображения. Тогда для каждого лица нужен нейрон с миллионом дендритов, что нереально. А теперь разделим все пиксели на мета-кластеры, такие как глаза, нос, уши и так далее. Всего десять таких мета-кластеров. Пусть в каждом мета-кластере будет десять кластеров, десять вариантов носа, десять вариантов ушей и так для всего. Теперь, чтобы запомнить лицо, достаточно нейрона с десятью дендритами. Это снижает объем памяти (ну и объем мозга) на пять порядков.
Заключение
А теперь, если допустить, что мозг состоит из мета-кластеров, можно попытаться рассмотреть с этой точки зрения некоторые понятия, присущие живому мозгу:
Кластеры необходимо постоянно обучать, иначе новые данные, не будут правильно обрабатываться. Для обучения кластеров в мозге нужна сбалансированная выборка. Поясню, если сейчас зима, то мозг будет учится только на зимних примерах, и полученные кластеры постепенно станут релевантными только зиме, а летом у этого мозга все будет плохо. Что с этим делать? Нужно периодически на все кластеризаторы подавать не только новые, но и старые важные примеры (воспоминания и зимы и лета). И чтобы этим воспоминаниям не мешали текущие ощущения, нужно органы чувств временно отключить. У животных это называется сон.
Представьте, мозг видит что-то маленькое, СЕРЕНЬКОЕ, которое бежит. После мета-кластеризации имеем три активных нейрона в трех мета-кластерах. И благодаря воспоминанию, мозг знает, что это вкусно. Потом, мозг видит что-то маленькое, СИНЕНЬКОЕ, которое бежит. Но мозг не знает, вкусно это или страшно. Достаточно временно отключить мета-кластер, где находятся цвета, и останется только маленькое, которое бежит. А мозг знает это это вкусно. Это называется аналогия.
Допустим, мозг вспомнил что-то, а потом, изменил активный нейрон-кластер в какой-то группе на любой другой, при этом в остальных мета-кластерах остается реальное воспоминание. И вот, мозг уже представил что-то такое, что никогда раньше не видел. А это уже воображение.
Спасибо за внимание, код здесь.
