Привет! Меня зовут Софья Лисичкина, я старший дата-аналитик в Лемана Тех. Занимаюсь системой эффективного управления ассортиментом — проще говоря, делаю так, чтобы нужные товары оказывались в нужном месте в нужное время.
Хочу поделиться опытом применения рядов Фурье для автоматического определения сезонных товаров. Статья будет полезна аналитикам данных, категорийным менеджерам, специалистам по цепи поставок — всем, кто принимает решения об ассортименте и запасах на основе данных.

Что вы узнаете
Как из формулы сделать рабочий инструмент (без воды)
Весь путь: от «нам нужно...» до «работает!»
Почему мы не стали городить ML-модели, а выбрали простое решение
Как объяснить бизнесу, что такое амплитуды и фазы Фурье
Контекст задачи
Сезонность бывает разной: внутринедельная, внутримесячная, внутригодовая. Способы ее детектирования зависят от цели и специфики бизнеса. В нашем случае нужно было учесть несколько факторов.
Бизнес-процессы компании — решения принимаются на стратегическом уровне
Новинки — как быть с SKU, по которым просто нет исторических данных
Объем данных — накопление статистики по каждому SKU создает избыточную нагрузку
Наша цель — понять, какие категории товаров сезонные, а какие нет и когда эти сезоны начинаются и заканчиваются. Звучит просто, но это основа для кучи стратегических решений — от планирования ассортимента на год вперед до понимания, когда категория «просыпается» и когда «засыпает». Работаем на уровне всей страны, минимальный шаг — месяц (потому что перестраивать ассортимент каждый день — это уже не стратегия, а хаос).
Как мы это используем, зная месяц входа и выхода
Планируем закупки заранее (за 2–3 месяца до старта сезона)
Расширяем ассортимент в начале сезона и сокращаем после пика
Распродаем остатки на выходе из сезона
Автоматом присваиваем сезонность новинкам. Запустили новую газонокосилку? Она сразу получает весенне-летний паттерн своей категории и попадает в план закупок на февраль-март, без ожидания накопления собственной статистики
Почему не взяли готовую коробку? Существующие типовые решения наподобие SAP или Oracle Retail заточены под другое: они прогнозируют, сколько конкретных SKU нужно завезти в конкретный магазин в следующем месяце. Для этого им нужна длинная история по каждому товару. Запустили новинку? Ждите полгода-год, пока модель наберет статистику. Плюс эти системы — черные ящики: попробуй объясни category-менеджеру, почему нейронка решила, что газонокосилки сезонные, а удобрения — нет.
Нам нужно было что-то другое: прозрачное, работающее на уровне категорий (чтобы новинки автоматом получали характеристики своей группы) и, главное, то, что можно показать бизнесу и сказать: «Вот почему эта категория сезонная, вот ее пик, вот математика».
У руководителей различных ассортиментных направлений Лемана ПРО есть обоснованное понимание сезонности: например, газонокосилки — это весна‑лето. Тем не менее внешние условия иногда вносят коррективы. Помните аномально теплую зиму 2024–2025? Такие штуки меняют паттерны спроса, и нужны данные за несколько лет, чтобы отличить тренд от случайности.
Ключевые ограничения методологии
Гранулярность. Минимальный период — 1 месяц. Это сознательный выбор: операционные команды не могут перестраивать ассортимент ежедневно, а помесячная детализация дает стабильность в планировании без избыточной волатильности.
Уровень агрегации. Расчет ведется на уровне целой товарной категории, а не по отдельным SKU. Это означает, что категория либо сезонная целиком, либо нет. Подход решает проблему холодного старта для новинок, при этом обеспечиваем ассортиментную однородность. В более крупной гранулярности (подотдел, тип) мы рискуем захватить два варианта сезонности: например, в подотделе «Удобрения» у нас могут быть как удобрения для комнатных растений, так и удобрения для газона. В первом случае сезонность будет отсутствовать.
Временной горизонт. Берем минимум 2 полных года данных. Это страховка от погодных аномалий конкретного года и возможность поймать тренды, которые разворачиваются дольше одного сезона. Почему взяли минимальный объем данных?
Актуальность: в ритейле ассортимент и категории меняются быстро. Категория многолетней давности может иметь совсем другую структуру продаж. Мы сознательно жертвуем глубиной истории ради актуальности.
Бизнес-реальность: внутренние процессы компании также сильно меняют структуру данных: смена операционных процессов, ввод и вывод брендов — все это быстро меняет бизнес.
Тип сезонности. Методика заточена под годовую сезонность с одним пиком. Да, ряды Фурье теоретически умеют работать с высшими гармониками и ловить сложные паттерны, но мы остановились на первой гармонике. Почему?
Простота для бизнеса — высшие гармоники усложняют картину, и объяснить операционным командам, что с этим делать, становится квестом
Меньше ложных срабатываний — на агрегированных данных высшие гармоники часто цепляются за случайный шум, а не за настоящую сезонность. Первая гармоника вытаскивает главный паттерн и не отвлекается на мелочи
И, наконец, перейдем к математике.
Методология
Ряды Фурье: детектирование сезонности
Используем методологию разложения в ряд Фурье для определения сезонности. Почему именно Фурье?
Прозрачность: можно показать бизнесу синусоиду и сказать: «Вот ваш паттерн продаж».Физическая интерпретация: a₁ и b₁ напрямую связаны с тем, когда пик (зима/весна/лето/осень).
Работает на агрегатах: нам не нужна история по SKU, достаточно категории.
Детерминированность: при одних и тех же данных всегда одинаковый результат (в отличие от ML-моделей с разными инициализациями).
Что пробовали еще?
STL-декомпозиция (Seasonal and Trend decomposition using Loess) — классика временных рядов. Проблема: требует длинную историю по каждому SKU, плохо работает с пропусками в данных, и, главное, сложно объяснить бизнесу, как именно Loess решил, где тренд, а где сезонность.
Автокорреляционный анализ (ACF/PACF) — хорош для детектирования периодичности, но опять же: какой порог взять? Как объяснить category-менеджеру график автокорреляции? Плюс он не дает нам явного ответа на вопрос, когда сезон начинается и заканчивается.
Итак, остановились на Фурье.
Т. к. месяц начала данных — январь, то мы имеем возможность путем сравнения с синусоидой и косинусоидой определить период высокой и низкой сезонности по типу сходства.
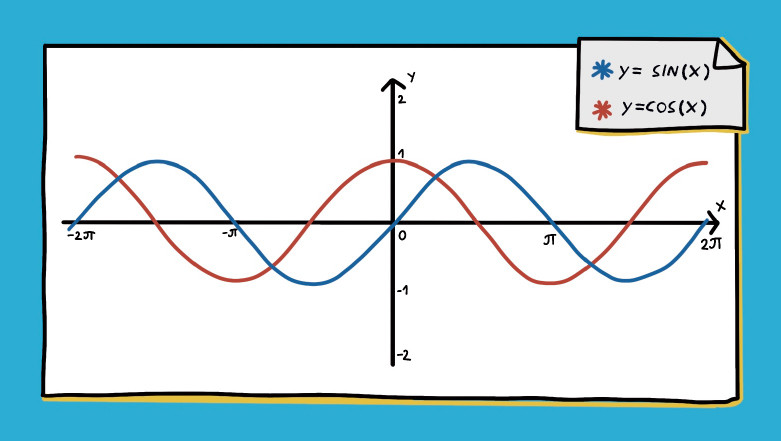
В случае, если кривая продаж сходна с косинусоидой либо обратна ей по коэффициенту Фурье, сможем задетектировать зимнюю (либо летнюю) высокую сезонность, в случае с синусоидой — весеннюю/осеннюю. Комбинация высоких коэффициентов даст возможность увидеть переходные сезоны.
Формулы расчетов
a₁ = (2/12) × Σ(i=1 to 12) monthly_sales_i × cos_values_i
b₁ = (2/12) × Σ(i=1 to 12) monthly_sales_i × sin_values_i
Определение пикового месяца через фазу
Для определения месяца входа и выхода товарной категории нам потребуется понимание фазы и пикового месяца.
Что такое фаза
Фаза — это сдвиг по времени относительно стандартной синусоиды или косинусоиды.
Измеряется с помощью двухаргументного арктангенса (в отличие от обычного, он изменяется на 360 градусов, что позволит нам учитывать положительные и отрицательные коэффициенты a₁, b₁).
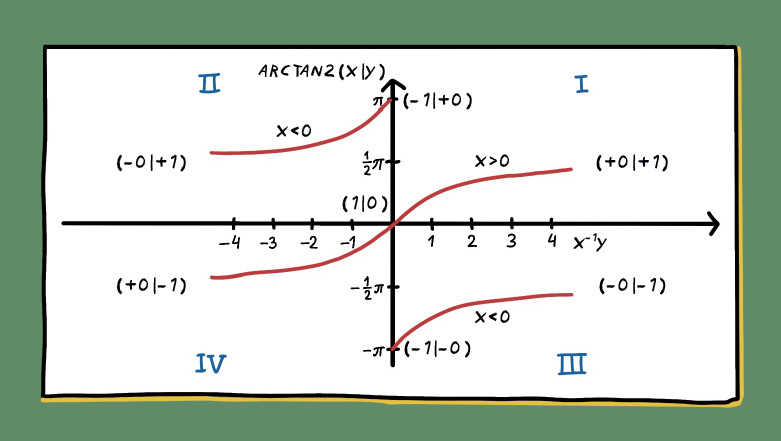
В физическом мире это будет означать следующее:
• a₁, b₁ > 0 — I квадрант → зимне-весенний пик
• a₁ < 0, b₁ > 0 — II квадрант → весенне-летний пик
• a₁ > 0, b₁ < 0 — III квадрант → летне-осенний пик
• a₁, b₁ < 0 — IV квадрант → осенне-зимний пик
Таким образом, arctan2(b₁, a₁) = угол от оси x до точки (a₁, b₁). Этот угол и есть фаза — он показывает, на сколько наша волна «повернута» относительно стандартного косинуса.
Зная это, ищем месяц пика:
peak_month_continuous = (-phase × 12) / (2π) mod 12
где:
• phase — угол в радианах (от -π до +π)
• phase × 12 / (2π) — переводим радианы в месяцы (2π радиан = 12 месяцев)
• -phase — минус нужен из-за математических соглашений (косинус vs время)
• mod 12 — обеспечиваем, что результат в диапазоне 0-11
Нахождение месяца входа и выхода из сезона
На данный момент определяем простыми эвристиками. Мы уже нашли месяц пика, а также рассчитали среднее значение. Далее вычисляем адаптивные пороги:
high_threshold = mean_value + 0.3 × (peak_value - mean_value)
low_threshold = mean_value + 0.1 × (peak_value - mean_value)
Находим в обе стороны от пика месяц старта и месяц конца сезона.
Пример расчета
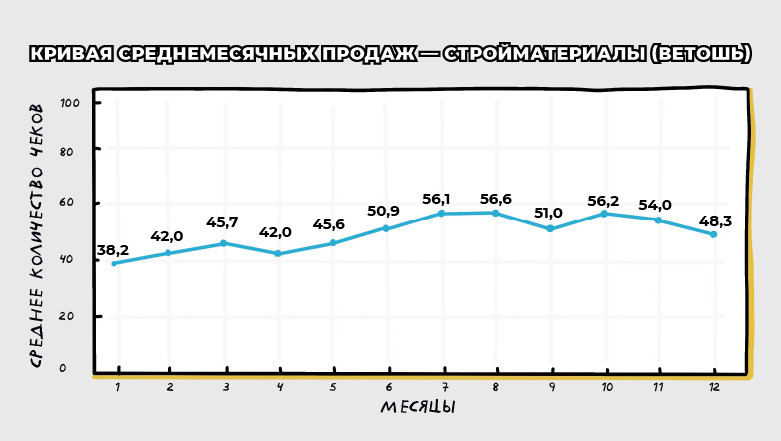
Возьмем три примера с зимней, весенней и отсутствующей сезонностью, посмотрим на графики продаж.
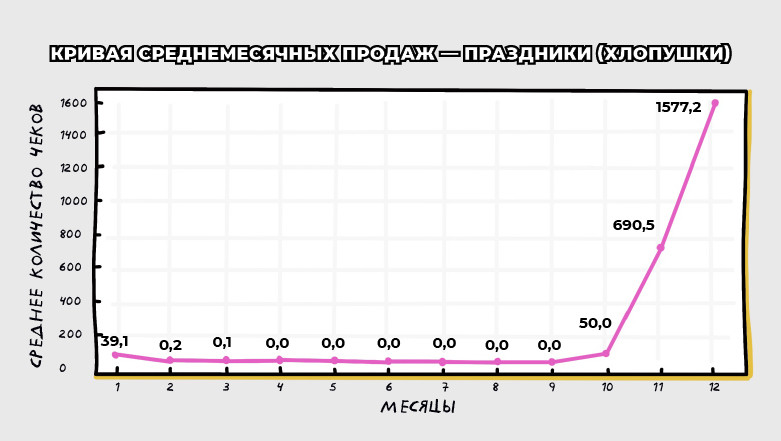
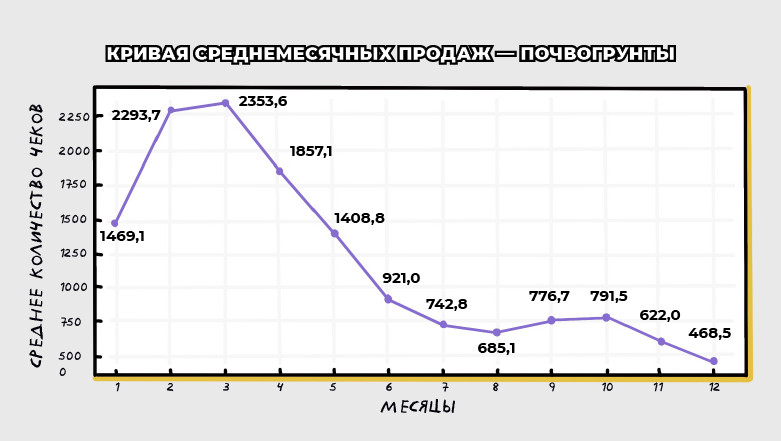
Косинус «качается» так:
• Январь = максимум (пик в начале года)
• Июль = минимум (спад в середине года)
• Декабрь = снова максимум
Косинусы месяцев: [1.0, 0.87, 0.5, 0.0, -0.5, -0.87, -1.0, -0.87, -0.5, 0.0, 0.5, 0.87]
Синус «качается» так:
• Январь = среднее значение
• Апрель = максимум (пик весной)
• Июль = среднее значение
• Октябрь = минимум (спад осенью)
Синусы месяцев: [0.0, 0.5, 0.87, 1.0, 0.87, 0.5, 0.0, -0.5, -0.87, -1.0, -0.87, -0.5]
Проверим каждый из графиков выше — насколько он похож на косинус и на синус? Найдем коэффициенты по формулам:
a₁ = (2/12) × Σ(i=1 to 12) monthly_sales_i × cos_values_i
b₁ = (2/12) × Σ(i=1 to 12) monthly_sales_i × sin_values_i
Как это работает
Для каждого месяца (от 1 до 12) мы берем фактические продажи и умножаем их на соответствующее значение косинуса и синуса из заранее рассчитанных массивов.
Пример расчета для категории «Почвогрунты»
Расчет a₁ (сходство с косинусом):
a₁ = (2/12) × [450×1.0 + 620×0.87 + 1350×0.5 + 1890×0.0 + 2150×(-0.5) + 1820×(-0.87) + 1430×(-1.0) + 980×(-0.87) + 750×(-0.5) + 580×0.0 + 470×0.5 + 420×0.87]
a₁ = (2/12) × [450 + 539.4 + 675 + 0 - 1075 - 1583.4 - 1430 - 852.6 - 375 + 0 + 235 + 365.4]
a₁ = (2/12) × 2122.54 ≈ 353.76
Расчет b₁ (сходство с синусом):
b₁ = (2/12) × [450×0.0 + 620×0.5 + 1350×0.87 + 1890×1.0 + 2150×0.87 + 1820×0.5 + 1430×0.0 + 980×(-0.5) + 750×(-0.87) + 580×(-1.0) + 470×(-0.87) + 420×(-0.5)]
b₁ = (2/12) × [0 + 310 + 1174.5 + 1890 + 1870.5 + 910 + 0 - 490 - 652.5 - 580 - 408.9 - 210]
b₁ = (2/12) × 4141.57 ≈ 690.52
А также коэффициент a₀, который будет равен среднему значению в каждом случае. Используем его для перевзвешивания (нам нужно понимать, насколько радикальны найденные нами коэффициенты).
Таблица 1. Коэффициенты Фурье
Категория | a₁ | b₁ | a₀ |
Почвогрунты | 353.757 | 690.523 | 1199.169 |
Праздники | 291.740 | -239.383 | 196.435 |
Ветошь | -5.213 | -5.332 | 48.885 |
Далее вычислим амплитуду сезонности по формуле для каждого случая:
amplitude = √(a₁² + b₁²)
Таблица 2. Амплитуда сезонности
Категория | a₁ | b₁ | a₀ | amplitude |
Почвогрунты | 353.757 | 690.523 | 1199.169 | 775.865 |
Праздники | 291.740 | -239.383 | 196.435 | 377.381 |
Ветошь | -5.213 | -5.332 | 48.885 | 7.457 |
Физический смысл
• Почвогрунты: a₁ = 353 и b₁ = 690 → продажи немного похожи на косинус, но меньше, чем на синус, — на синус они похожи сильно. Следовательно, пик будет весной, а начинаться сезон продаж будет в начале года. Амплитуда ≈ 775 → общая «сила качания» сезонности — товар очень сезонный
• Праздники: a₁ = 291 и b₁ = -239 → продажи очень похожи на косинус, но также на «перевернутый» синус. Следовательно, пик будет зимой, а начинаться сезон продаж будет в конце осени. Амплитуда ≈ 377 → общая «сила качания» сезонности — товар очень сезонный
• Ветошь: a₁ = -5 и b₁ = -5 → продажи не похожи ни на синус, ни на косинус. Амплитуда ≈ 7 → общая «сила качания» сезонности — товар несезонный
И далее нормализуем амплитуду на среднее значение продаж. Это значит, что мы делим amplitude на a₀, чтобы понять, насколько радикальна эта амплитуда относительно среднего.
Таблица 3. Сила сезонности
Категория | a₁ | b₁ | a₀ | amplitude | seasonality_strength |
Почвогрунты | 353.757 | 690.523 | 1199.169 | 775.865 | 64,70% |
Праздники | 291.740 | -239.383 | 196.435 | 377.381 | 192,12% |
Ветошь | -5.213 | -5.332 | 48.885 | 7.457 | 15,25% |
Определение пикового месяца
Посмотрим на фазу для каждой категории.
Почвогрунты:
φ = arctan2(-690.52, 353.76) = -1.097 рад
t_пик = (-φ × 12) / (2π) mod 12
t_пик = (1.097 × 12) / 6.28318 mod 12 = 2.096
M_пик = ⌊t_пик + 0.5⌋ + 1
M_пик = ⌊2.096 + 0.5⌋ + 1 = 3
Результат: март для почвогрунтов.
Праздники (хлопушки):
φ = arctan2(-239.38, 291.74) = -0.693 рад
t_пик = (-(-0.693) × 12) / (2 × 3.14159) mod 12
t_пик = (0.693 × 12) / 6.28318 mod 12 = 1.324
Но поскольку b₁ отрицательный, корректируем:
t_пик = 12 - 1.324 = 10.676
M_пик = ⌊10.676 + 0.5⌋ + 1 = 12
Результат: декабрь для праздников.
Ветошь:
φ = arctan2(-5.332, -5.213) = -2.354 рад
t_пик = (-(-2.354) × 12) / (2 × 3.14159) mod 12
t_пик = (2.354 × 12) / 6.28318 mod 12 = 4.497
M_пик = ⌊4.497 + 0.5⌋ + 1 = 5
Результат: май для ветоши (?).
Но это сомнительный результат, так как амплитуда слишком мала.
Дополнительные проверки
Нужны для того, чтобы убедиться, что выводы методологии применимы в бизнес-процессах. Помните наше ограничение по количеству данных? Уступка в пользу бизнеса может нанести ущерб математической достоверности модели. Что считаем?
• Коэффициент детерминации линейного тренда R²
• Автокорреляция первого порядка
• Коэффициент монотонности (доля изменений в одном направлении)
• Коэффициент гладкости
Посмотрим на примере, как сработает с ветошью.
Хотя ветошь была посчитана ошибочно сезонной, R² эту ошибку исправил:
R² = 0.12 (при пороге R² < 0.4 категория признается несезонной).
Также он показал высокую автокорреляцию, что указывает на тренд, а не на сезонность.
Нахождение границ сезона
Далее ищем месяц старта и месяц конца сезона для сезонных категорий.
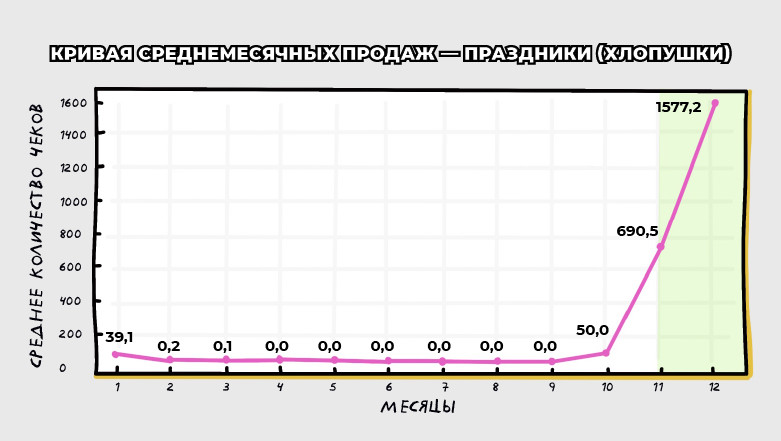
Праздники (хлопушки):
Пиковый месяц: декабрь
Среднее значение (mean_value): 196.44
Пиковое значение (peak_value): 573.8
high_threshold = mean_value + 0.3 × (peak_value - mean_value)
high_threshold = 196.44 + 0.3 × (573.8 - 196.44) = 309.6
low_threshold = mean_value + 0.1 × (peak_value - mean_value)
low_threshold = 196.44 + 0.1 × (573.8 - 196.44) = 234.2
От пика (декабрь) идем вправо до high_threshold → находим месяц окончания сезона.
От пика идем влево до low_threshold → находим месяц начала сезона.
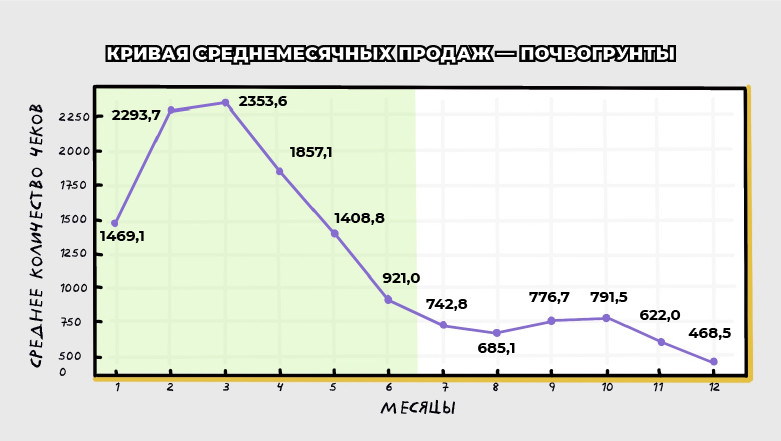
Почвогрунты:
Пиковый месяц: март
Среднее значение (mean_value): 1199.17
Пиковое значение (peak_value): 2353.6
high_threshold = mean_value + 0.3 × (peak_value - mean_value)
high_threshold = 1199.17 + 0.3 × (2353.6 - 1199.17) = 1545.5
low_threshold = mean_value + 0.1 × (peak_value - mean_value)
low_threshold = 1199.17 + 0.1 × (2353.6 - 1199.17) = 1314.6
От пика (март) идем вправо до high_threshold → находим месяц окончания сезона.
От пика идем влево до low_threshold → находим месяц начала сезона.
Валидация результатов
Есть несколько возможных вариантов.
1. Сезонные отделы. Мы знаем, что часть отделов (например «Сад») является остро сезонными, другие — в меньшей степени. Используем это бизнес-знание для понимания общей картины.
Итак, посчитаем долю уникальных SKU, которые являются сезонными в том или ином отделе.
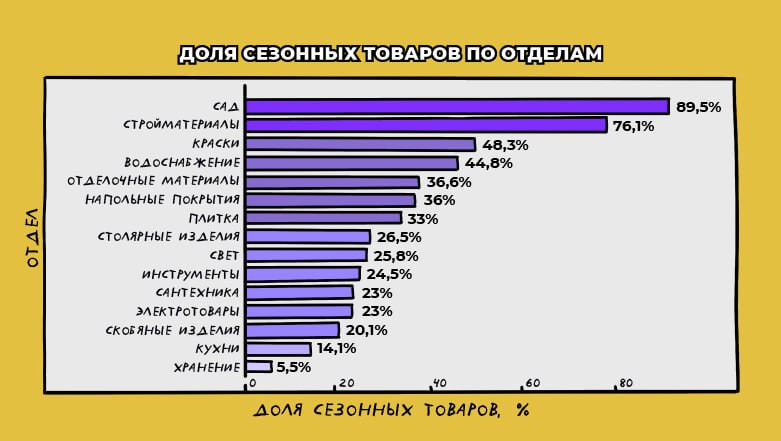
2. Обратимся к руководителям ассортиментных направлений, чтобы проанализировать результаты более детально. Результат можно увидеть на тепловой карте ниже.
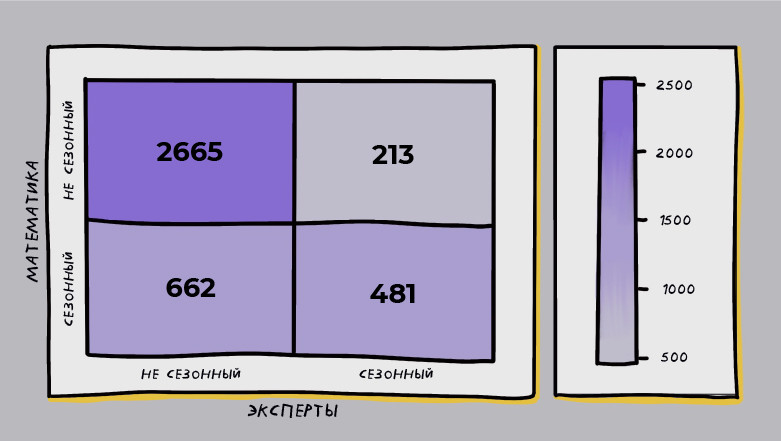
Эксперты и математика согласны в 78.24 процента случаев
Математика посчитала сезонным, а эксперты — нет 16.46 процента случаев
Эксперты посчитали сезонными, а математика — нет 5.30 процента случаев
Заключение
Мы взяли классическую математику из учебника и превратили ее в рабочий инструмент для управления ассортиментом. Никакого ML, никаких черных ящиков — только ряды Фурье и здравый смысл.
Что в итоге
Математика, которую можно объяснить, — мы решаем проблему доверия к данным: показываем категорийному менеджеру графики с синусоидами, и он понимает, почему его категория сезонная. Не «так модель решила», а «вот смотрите, ваши продажи качаются как косинус»
Новинки работают из коробки — запустили новый SKU в категории «Газонокосилки»? Он автоматом получает весенне-летнюю сезонность. Не нужно ждать год, пока накопится статистика
Масштаб без боли — обрабатываем десятки тысяч товаров, не городя ML-инфраструктуру и не нанимая дата-сайентистов для настройки моделей
Бизнес согласен в 78% случаев — это хороший показатель. Оставшиеся 22% расхождений — это либо мы нашли то, что эксперты пропустили, либо наоборот (и то, и то полезно обсуждать)
Почему это вообще важно?
Потому что решения об ассортименте нельзя принимать на интуиции, особенно когда климат меняется, а с ним и паттерны спроса. Теплая зима? Сдвиг весеннего сезона? Данные за 2–3 года покажут, это тренд или случайность. При человеческом же управлении ошибки неизбежны, и их цена измеряется в миллионах при взгляде на год.
Что дальше?
Сейчас система ловит категории с одним пиком в году (газонокосилки летом, елочные игрушки зимой). Следующий шаг — научить ее работать с более сложными паттернами: удобрения с весенним и осенним пиками или категории, которые из сезонных превращаются в круглогодичные.
Если будут вопросы по деталям реализации — пишите в комментариях, обсудим!
