Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
Хабр доступен 24/7 благодаря поддержке друзей
Комментарии 56
Это первый пост на хабре. Потому заранее прошу прощения за никакое оформление кода, и, возможно, тафтологию в тексте.
А скорость не замерял?
Хотябы для сравнения с qsort stl'ным. Просто на таких маленьких объемах данных может получится так что пересылка в видеопамять+вызов куды, займет больше времени чем простая сортировка.
Еще немного не понятно почему используется K[tid]? Это shared память? Вообще надо постараться сделать так, чтобы вместо K[tid] использовалась регистровая память, но насколько я помню в CUDA нет способов явно указывать на использование регистров.
Хотябы для сравнения с qsort stl'ным. Просто на таких маленьких объемах данных может получится так что пересылка в видеопамять+вызов куды, займет больше времени чем простая сортировка.
Еще немного не понятно почему используется K[tid]? Это shared память? Вообще надо постараться сделать так, чтобы вместо K[tid] использовалась регистровая память, но насколько я помню в CUDA нет способов явно указывать на использование регистров.
Дело в том что задача возникла, когда выполнение УЖЕ идет в ядре видеопроцессора, и необходимо было быстро отсортировать память находясь там без выхода наружу. Соглашусь что потери на копирование данных имеют место когда надо копировать. Но когда память уже была там и мы просто запускаем kernel и выходим из него используя данные уже находящиеся там — то qsort там нет.
И действительно, можно вообще избавиться от K[tid]. И соптимизировать по скорости. Добавил UPD2.
И действительно, можно вообще избавиться от K[tid]. И соптимизировать по скорости. Добавил UPD2.
Я так понимаю, что в UPD2 строчку под номером (2) можно перенести в начало, и в блоке (1) использовать B_tid вместо A[tid]?
Нет, т.к. после синхронизации п.4 выполняется параллельно и A[tid] до выполнения текущим потоком мог уже затереться другим потоком. Если бы A[] был локальным то можно было, а он в __shared__ потому и нельзя.
в первом потке A[4] = A[0];
во втором A[0] = A[4] (а он уже A[0]);
И при сортировке массива 5 1 получим 5 5 или 1 1.
Может быть и такой случай 1 3 2 даст 1 2 2, и т.д.
Для этого и проводится запоминание текущего элемента в B_tid чтобы избежать перезатирания его соседом.
в первом потке A[4] = A[0];
во втором A[0] = A[4] (а он уже A[0]);
И при сортировке массива 5 1 получим 5 5 или 1 1.
Может быть и такой случай 1 3 2 даст 1 2 2, и т.д.
Для этого и проводится запоминание текущего элемента в B_tid чтобы избежать перезатирания его соседом.
Хм, может я неверно понимаю что делает __syncthreads?
Потому что любой поток в этом месте будет ждать, пока остальные потоки доберутся до точки синхронизации.
И так как в той области нет изменений A[] (изменения только в п.4), то, по идее, неважно, в каком месте той области (до синхронизации) мы запоминаем значение A[tid].
Потому что любой поток в этом месте будет ждать, пока остальные потоки доберутся до точки синхронизации.
И так как в той области нет изменений A[] (изменения только в п.4), то, по идее, неважно, в каком месте той области (до синхронизации) мы запоминаем значение A[tid].
Запоминание «B_tid» перед синхронизацией — верное, но я не об этом.
Вы наверное о том, что A[tid] можно прочитать один раз перед циклом, а потом использовать уже локальную копию? Тогда не будет обращений к памяти на каждой итерации(правда его и так скорее всего не будет, если кеша хватит).
А если бы мы молотили большие объемы данных, то да, скорость бы заметно возрасла, потому что мы снижаем колличество операций обращений к памяти до 1 за итерацию цикла. Еще в какойнибудь коалесинг можно попасть, и получить прирост производительности более чем в 2 раза ;) Ну и это еще при условии что компилятор тупой и сам не заметил что переменная в цикле не зависит от изменяемой величины.
А если бы мы молотили большие объемы данных, то да, скорость бы заметно возрасла, потому что мы снижаем колличество операций обращений к памяти до 1 за итерацию цикла. Еще в какойнибудь коалесинг можно попасть, и получить прирост производительности более чем в 2 раза ;) Ну и это еще при условии что компилятор тупой и сам не заметил что переменная в цикле не зависит от изменяемой величины.
Да, вы правы.
Поправил UPD2.
Еще можно убрать IF (вообще в CUDA нужно избегать IF'ов, они значительно замедляют выполнение программы).
По моим поверхностным тестам(корректность сортировки я не проверял %) ) на цикле прирост производительности на 18% :) Думаю еще можно выжать, если позаниматься оптимизацие обращения к памяти и выравниванием массива.
if (A[i]<B_tid) K_tid++;можно заменить на
K_tid+=(A[i]<B_tid);
По моим поверхностным тестам(корректность сортировки я не проверял %) ) на цикле прирост производительности на 18% :) Думаю еще можно выжать, если позаниматься оптимизацие обращения к памяти и выравниванием массива.
Надо проверить. Проверю на 1млн итераций. Если будет лучше — исправлю.
Но вообще странно.
Здесь if (A[i]<B_tid) K_tid++; на лицо всего 2 операции если IF-выполнился.
А здесь K_tid+=(A[i]<B_tid); всегда минимум 2.
Но вообще странно.
Здесь if (A[i]<B_tid) K_tid++; на лицо всего 2 операции если IF-выполнился.
А здесь K_tid+=(A[i]<B_tid); всегда минимум 2.
Отпишись как проверишь ;) Очень удивлюсь если мой вариант окажется медленней. Дело в том что у всех этих мультипроцессоров(SM) архитектура близкая к SIMD. И каждый condition приводит либо к выполнению обоих веток последовательно, либо к обработке в один поток.
И кстати в том числе по этой же причине циклы в CUDA тоже рекомендуют разворачивать(там шаманства с рекурсией через темплейты ;) ).
И кстати в том числе по этой же причине циклы в CUDA тоже рекомендуют разворачивать(там шаманства с рекурсией через темплейты ;) ).
Да, я писал именно про это. Странно, что меня сразу не поняли.
Вот пример для демонстрации работы данного алгоритма для языка python:
array_i = [94, 89, 238, 121, 244, 64, 175, 60, 166, 181, 77, 24, 111, 0, 47, 212, 68, 76, 174, 124, 40, 227, 123, 101, 58, 177, 148, 134, 36, 21]
array_k = [ 0 ]*len(array_i)
array_o = [ None ]*len(array_i)
for i1, c1 in enumerate(array_i):
cnt = 0
for i2, c2 in enumerate(array_i):
if c1 > c2:
cnt += 1
elif c1 == c2 and i1 < i2:
cnt += 1
array_k[i1] = cnt
for i, k in enumerate(array_k):
array_o[k] = array_i[i]
print "array_i =", array_i
print "array_o =", array_o
Ваш алгоритм выполняется в одном потоке? Если так — то у него виден сразу вложенный «for». Это значит что его сложность O(N^2). Это крайне медленно.
Если бы Вы написали на С++ (MSVS2010 + STD::TR1) и вместо первого «for» поставили бы parallel_for, то это был бы описанный алгоритм со временем выполнения для O(N).
Если бы Вы написали на С++ (MSVS2010 + STD::TR1) и вместо первого «for» поставили бы parallel_for, то это был бы описанный алгоритм со временем выполнения для O(N).
и то, только в случае, если количество элементов равно количеству ядер процессора.
Если будете применять, пожалуйста не забывайте, что данный алгоритм применим только для GPU, когда количество потоков равно количеству сортируемых элементов. Чем мощнее видеокарта — тем больший массив без потери скорости можно сортировать.
Для CPU он не подходит.
Если будете применять, пожалуйста не забывайте, что данный алгоритм применим только для GPU, когда количество потоков равно количеству сортируемых элементов. Чем мощнее видеокарта — тем больший массив без потери скорости можно сортировать.
Для CPU он не подходит.
Само собой разумеется :) На обычных процессорах в последовательном исполнении получим O(n*n), что может дать и пузырек. Пример на python показателен тем, что в нем наглядно видно, что сортировать можно не только цифры, а все, для чего определима функция сравнения. Что же касается массивов, размерностью превышающих MaxThreads, то входной массив тогда лучше всего фрагментировать в несколько размерностью MaxThreads, после чего досортировать через MergeSort.
Эт для наглядности, и только. Понятно, что первый цикл может выполняться в параллель. Получаем, что уже не O(N^2), а O(N*k), где k = ОкруглениеДоМинимальнойЦелойГраницыСверху(N/MaxThreads). Если выполняется условие (0 < N <= MaxThreads) — то константа k выродится в единицу, откуда следует что в этом частном случае сложность будет O(N).
Вы евангелист Microsoft? :)
Очень классная визуализация метода с википедии
Хороший пост, спасибо. А как вы думаете, неужели OpenCL не поборет CUDA?
Одобряю и поддерживаю OpenCL т.к. видеокарты ATI быстрее чем NVidia. И тенденция преимущества производительности ATI идет уже очень давно. Но вот поддержка драйверов, да и вообще суппорт у ATI слабее, чем у NVidia. Так, когда CUDA только зарождалась и завоевывала рынок, у ATI все только начиналось. Теперь же, пару лет спустя, CUDA значительно сильнее развилась чем конкуренты. Появились такие средства, как parallel nsight monitor, изначально созданные и соптимизированные именно для CUDA.
Каждый же производитель видеокарт оптимизирует свою продукцию под свою технологию разработки ПО. Потому если хочется писать на CUDA — сейчас приходится выбирать Nvidia и терять в 5% (по разному конечно, вопрос спорный) производительности.
Понимая что долго так не продолжится, обе компании поддерживают OpenCL, но так… чтобы было. А предпочтение отдадут своим продуктам. И так будет долго, так как Nvidia не допустит конкуренцию у разработчиков игр и программ, которые на данный момент пишут в основном для CUDA, а не Stream.
Каждый же производитель видеокарт оптимизирует свою продукцию под свою технологию разработки ПО. Потому если хочется писать на CUDA — сейчас приходится выбирать Nvidia и терять в 5% (по разному конечно, вопрос спорный) производительности.
Понимая что долго так не продолжится, обе компании поддерживают OpenCL, но так… чтобы было. А предпочтение отдадут своим продуктам. И так будет долго, так как Nvidia не допустит конкуренцию у разработчиков игр и программ, которые на данный момент пишут в основном для CUDA, а не Stream.
А по другим исследованиям, ATiStream тормознее, чем CUDA, намного.
www.pcper.com/article.php?aid=745
www.pcper.com/article.php?aid=745
Думал-думал и придумал! :)
Условие на уникальность элементов можно снять следующим способом:
if (A[i]<A[tid] || A[i]==A[tid] && i<tid)
K_tid++; //позиция в результате
Условие на уникальность элементов можно снять следующим способом:
if (A[i]<A[tid] || A[i]==A[tid] && i<tid)
K_tid++; //позиция в результате
Хороший пост. Но будьте осторожны с заявлениями О(n).
Это предполагает, что n любым (больше определенной константы).
Само собой для бесконечного n вы не наберете процессоров.
Извините за придирку, но это важно.
Так и задачу коммивояжера за линейное время можно решить :).
Это предполагает, что n любым (больше определенной константы).
Само собой для бесконечного n вы не наберете процессоров.
Извините за придирку, но это важно.
Так и задачу коммивояжера за линейное время можно решить :).
Полностью согласен! Про «любые» массивы сразу все оговорки были сделаны :)
Сейчас настала пора облачных вычислений, потому и
>>задачу коммивояжера за линейное время можно решить.
Вопрос только в том, что больше «любой» размер массива, или «любое» количество вычислителей в облаке.
Вопрос о сложности был еще со времен создания RSA. Где математики считали что будет неимоверно сложно раскладывать числа на сомножители. Но время показало, что понятие сложность имеет свою размерность. И если данных для вычислений мало, мощности много, то сложностью можно и пренебречь.
Сейчас настала пора облачных вычислений, потому и
>>задачу коммивояжера за линейное время можно решить.
Вопрос только в том, что больше «любой» размер массива, или «любое» количество вычислителей в облаке.
Вопрос о сложности был еще со времен создания RSA. Где математики считали что будет неимоверно сложно раскладывать числа на сомножители. Но время показало, что понятие сложность имеет свою размерность. И если данных для вычислений мало, мощности много, то сложностью можно и пренебречь.
Да я вас понял. Просто понятие имеет в особое значение.
А что касается «пренебречь» — то тут согласиться не могу. Сложность алгоритмов вещь злобная. К примеру, если мы решаем задачу коммивояжера с операцией в одну микросекунду (10^(-6)), то для поиска по n городам нам потребуется:
10 — 0,001 секунда
30 — 1073 секунды
50 — 1125899906.8426239 секунд или около 35 лет
Вроде данных и не много, но O(2^n) это тяжело. Тут хоть какие ресурсы бери, все равно сольем. А на счет криптографии: ломать то можно. Но часто это дороже, чем то ради чего ломаешь.
А что касается «пренебречь» — то тут согласиться не могу. Сложность алгоритмов вещь злобная. К примеру, если мы решаем задачу коммивояжера с операцией в одну микросекунду (10^(-6)), то для поиска по n городам нам потребуется:
10 — 0,001 секунда
30 — 1073 секунды
50 — 1125899906.8426239 секунд или около 35 лет
Вроде данных и не много, но O(2^n) это тяжело. Тут хоть какие ресурсы бери, все равно сольем. А на счет криптографии: ломать то можно. Но часто это дороже, чем то ради чего ломаешь.
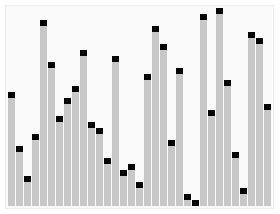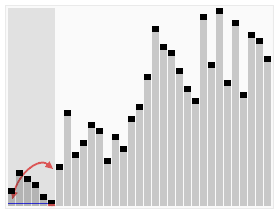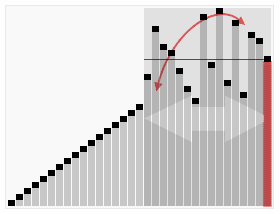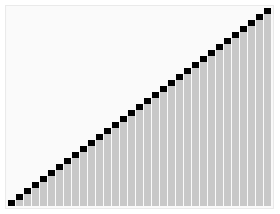
Сортировка массива за O(N)
O(N) — характеризует сложность алгоритма в зависимости от количества элементов (N). Поэтому даже при использовании миллиарда ядер для сортировки массива из миллиарда элементов, сложность этого алгоритма (который, кстати, называется «сортировка выбором») составит O(n²).
Временная сложность у приведенного алгоритма O(N).
Вычислительная же сложность, как и у алгоритма сортировки выбором равна O(N^2).
Если бы при решении задачи использовался алгоритм «сортировки выбором» это было бы максимум в N раз дольше, либо в log N раз дольше (случай с qsort).
Вычислительная же сложность, как и у алгоритма сортировки выбором равна O(N^2).
Если бы при решении задачи использовался алгоритм «сортировки выбором» это было бы максимум в N раз дольше, либо в log N раз дольше (случай с qsort).
Временная сложность у приведенного алгоритма O(N)
O(N²). Квадратичная сложность никуда не делась. Константный делитель, равный количеству параллельно работающих потоков, не значит ровным счетом ничего.
Если бы при решении задачи использовался алгоритм «сортировки выбором»
Что значит «если бы»? Это и есть сортировка выбором, адаптированная под многопоточность: www.sorting-algorithms.com/selection-sort: внешний цикл переложен на нити, а внутренний «удлинен», поскольку каждой нити необходимо сравнить свой элемент с остальными элементами массива. Или я что-то упускаю из виду?
Да, алгоритм действительно можно называть и «сортировкой выбором», адаптированной под многопоточность.
Но следует понимать, что все-таки это два разных алгоритма. И время выполнения одного != времени выполнения другого при использовании в решении указанной мной задачи (вместе с ее ограничениями).
И почему-то и авторы приведенной статьи, и другие, используют qsort и другие алгоритмы, т.к. они в старом смысле имеют лучшую стоимость (сложность) чем более медленные «сортировки выбором».
Но как я показал в данном посте, при многопоточных вычислениях понятие стоимости (сложности) несколько меняется и эффективнее использовать алгоритмы более медленные на CPU, но дающие более лучшие временные характеристики вычислений на GPU, чем общепринятые алгоритмы.
При создании квантовых же компьютеров или вычислений на графенах опять-таки картина может измениться.
Но следует понимать, что все-таки это два разных алгоритма. И время выполнения одного != времени выполнения другого при использовании в решении указанной мной задачи (вместе с ее ограничениями).
И почему-то и авторы приведенной статьи, и другие, используют qsort и другие алгоритмы, т.к. они в старом смысле имеют лучшую стоимость (сложность) чем более медленные «сортировки выбором».
Но как я показал в данном посте, при многопоточных вычислениях понятие стоимости (сложности) несколько меняется и эффективнее использовать алгоритмы более медленные на CPU, но дающие более лучшие временные характеристики вычислений на GPU, чем общепринятые алгоритмы.
При создании квантовых же компьютеров или вычислений на графенах опять-таки картина может измениться.
Нет, O оценка это O оценка и не стоит вводить людей в заблуждение, она характеризует количество выполняемых операций в целом. Заголовок выглядит очень желтушно.
А в интерпретации «на одно ядро GPU», ну или любой другой параллельной системы это уже совершенно другое.
А в интерпретации «на одно ядро GPU», ну или любой другой параллельной системы это уже совершенно другое.
Согласен с just_vladimir. Факторизацией, поиском и т.п. в промышленных масштабах тоже не на одном ядре обычно занимаются, однако никто не заявляет о временной сложности в O(N²/количество_ядер)
Во первых, те кто занимается таким поиском и найдет более быстрое решение — то и не заявит. Тем более не напишет статью на хабре о своем решении.
Во вторых, O(N²/количество_ядер) когда количество_ядер = N, значительно лучшем чем просто O(N^2) или O(N log N).
И если нет желания использовать большой сложный код для простой и быстрой сортировки, то можно использовать предлагаемый алгоритм. О чем и был пост, а не о постулатах сложности алгоритмов.
Минимум кода, максимум результата. Знаете другой алгоритм в одну строку с более быстрой скоростью работы в многопоточном режиме? С удовольствием прочту ваш пост про него (а такие алгоритмы наверняка есть, просто никто о них не заявляет на хабре).
Во вторых, O(N²/количество_ядер) когда количество_ядер = N, значительно лучшем чем просто O(N^2) или O(N log N).
И если нет желания использовать большой сложный код для простой и быстрой сортировки, то можно использовать предлагаемый алгоритм. О чем и был пост, а не о постулатах сложности алгоритмов.
Минимум кода, максимум результата. Знаете другой алгоритм в одну строку с более быстрой скоростью работы в многопоточном режиме? С удовольствием прочту ваш пост про него (а такие алгоритмы наверняка есть, просто никто о них не заявляет на хабре).
Во вторых, O(N²/количество_ядер) когда количество_ядер = N, значительно лучшем чем просто O(N^2) или O(N log N)
А с чего Вы решили, что алгоритмы имеющие сложность O(N*logN) не будут параллелиться?
И если нет желания использовать большой сложный код
Если он при этом работает эффективнее, то почему не должно быть желания его использовать?
PS: минус в карму за комментарий, как то низковато…
just_vladimir, отвечу по порядку.
1
Если считаете что qsort в частности хорошо параллелится, то приведите пожалуйста пример и его временную (да любую) сложность для сравнения. Раз вы задали такой вопрос и продолжаете писать комментарии, то ясно что причина в нехватке знаний. Цитирую:
2
При разработке, когда у вас есть желание использовать чужой якобы эффективный код необходимо его:
а) протестировать
б) осмыслить, проверить и проанализировать (вдруг там есть презент на пасху)
Для этого вам необходимо иметь свободное время и потратить определенное количество человеко-часов на проведение этих операций. Только по их окончании вы можете быть уверены что используемый код работает (и то не факт). У меня такого желания что-то не возникло… :).
Потому и решил поделиться с хабрасообществом простым решением в одну строку, решающим поставленную задачу.
И рад, что хоть кому-то оно понравилось! :-D
А вам потому и минус, что отсутствует желание думать, вникать и понимать. Хотя, может это и просто ваша невнимательность. Далее, претензии — в личку, а то вы уже перешли на оскорбления и начинаете троллить.
Всего хорошего!
1
А с чего Вы решили, что алгоритмы имеющие сложность O(N*logN) не будут параллелиться?Если вы внимательно читали пост, то вначале я привел пример распараллеленного qsort.
Если считаете что qsort в частности хорошо параллелится, то приведите пожалуйста пример и его временную (да любую) сложность для сравнения. Раз вы задали такой вопрос и продолжаете писать комментарии, то ясно что причина в нехватке знаний. Цитирую:
Основные ограничения CUDA:
* отсутствие поддержки рекурсии для выполняемых функций;
* минимальная ширина блока в 32 потока;
2
Если он при этом работает эффективнее, то почему не должно быть желания его использовать?
При разработке, когда у вас есть желание использовать чужой якобы эффективный код необходимо его:
а) протестировать
б) осмыслить, проверить и проанализировать (вдруг там есть презент на пасху)
Для этого вам необходимо иметь свободное время и потратить определенное количество человеко-часов на проведение этих операций. Только по их окончании вы можете быть уверены что используемый код работает (и то не факт). У меня такого желания что-то не возникло… :).
Потому и решил поделиться с хабрасообществом простым решением в одну строку, решающим поставленную задачу.
И рад, что хоть кому-то оно понравилось! :-D
А вам потому и минус, что отсутствует желание думать, вникать и понимать. Хотя, может это и просто ваша невнимательность. Далее, претензии — в личку, а то вы уже перешли на оскорбления и начинаете троллить.
Всего хорошего!
Хорошая статья, только код надо было бы оформить получше.
Также советую вам посмотреть сюда: code.google.com/p/back40computing/wiki/RadixSorting
Это самая быстрая реализация сортировки для массовых программируемых устройств.
На NVIDIA GTX480 средняя скорость для простых массивов 1 млрд. элементов / сек.
Также советую вам посмотреть сюда: code.google.com/p/back40computing/wiki/RadixSorting
Это самая быстрая реализация сортировки для массовых программируемых устройств.
На NVIDIA GTX480 средняя скорость для простых массивов 1 млрд. элементов / сек.
Ну и с O(n) вы погорячились. Это же всё-таки ассимптотика, поэтому у вас нелинейная сложность.
Конечно согласен! :) Да, да и еще раз да.
Временная сложность O(N), а не вычислительная. Вычислительная O(N^2).
Спасибо за линк!
Временная сложность O(N), а не вычислительная. Вычислительная O(N^2).
Спасибо за линк!
И последний раз про сложность и о чем был данный пост.
habrahabr.ru/blogs/algorithm/110177/#comment_3505922
Спасибо за внимание!
habrahabr.ru/blogs/algorithm/110177/#comment_3505922
Спасибо за внимание!
В статье ни разу не уточняется, что это за сложность, при том, что использованное Вами обозначение вполне устоявшееся и не совпадает с тем, что Вы имели в виду. Причем хочу заметить, что это даже не временная сложность, почитайте хотя бы вот этот не самый авторитетный источник.
В не самом авторитетном источнике ясно написано:
То есть, такие алгоритмы имеют временную сложность O(N).
Точного названия сложности сравнения в посте сказано не было, но позже было пояснено в комментарии от
И еще момент. Да, операции выполняются параллельно. Вы хотите сказать что параллельный алгоритм и последовательный — это одинаковые алгоритмы? И методы сортировки для последовательных алгоритмов эффективно применимы к параллельным?
Вам же желаю успешного окончания ПГТУ, советую пройти этот курс и выучить эту книгу, и хотя бы пролистать еще один не авторитетный источник.
Разговор с вами окончен. Всего хорошего!
Временная сложность алгоритма (в худшем случае) — это функция размера входных и выходных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера. В задачах, где размер выхода не превосходит или пропорционален размеру входа, можно рассматривать временную сложность как функцию размера только входных данных.
То есть, такие алгоритмы имеют временную сложность O(N).
Точного названия сложности сравнения в посте сказано не было, но позже было пояснено в комментарии от
edeldm * 17 декабря 2010, 19:54 *Поэтому замечание ваше неверное.
И еще момент. Да, операции выполняются параллельно. Вы хотите сказать что параллельный алгоритм и последовательный — это одинаковые алгоритмы? И методы сортировки для последовательных алгоритмов эффективно применимы к параллельным?
Вам же желаю успешного окончания ПГТУ, советую пройти этот курс и выучить эту книгу, и хотя бы пролистать еще один не авторитетный источник.
Разговор с вами окончен. Всего хорошего!
На самом действительно режут фразы:
" массив длиной до 1000 элементов (далее рассматривается и общий случай с большим значением, но у меня было так). Сортировать такой массив с O(NlogN) временем, имея 15000 потоков показалось как-то расточительно."
Как вообще определение O(f(x)) соотносится с ограничением x<1000?
Но это скорее к чистоте формулировок и глубине понимания как асимптотика работает. По сути вы вполне правы.
" массив длиной до 1000 элементов (далее рассматривается и общий случай с большим значением, но у меня было так). Сортировать такой массив с O(NlogN) временем, имея 15000 потоков показалось как-то расточительно."
Как вообще определение O(f(x)) соотносится с ограничением x<1000?
Но это скорее к чистоте формулировок и глубине понимания как асимптотика работает. По сути вы вполне правы.
Как вообще определение O(f(x)) соотносится с ограничением x<1000?В посте хотел показать что рассматривались алгоритмы сортировки в диапазоне ArraySize <= MaxThreads. И если так ограничить размер исходного массива, то выбор используемого алгоритма сортировки следует осуществлять несколько «переосмыслив» их эффективность. И в качестве критерия выбора предложил
Если такой критерий не вводить, то становится трудно сравнивать алгоритмы в поставленных рамках задачи. А общепринятое понятие
Анализируя комментарии здесь все больше прихожу к выводу, что было бы неплохо написать вообще обзор параллельных алгоритмов сортировки. Потому как те алгоритмы, которые в пространстве последовательного выполнения хороши, могут оказаться не столь эффективны в параллельном, как например тот же qsort.
Но с такой яростной критикой хабрапользователей уже сомневаюсь, что правильно поймут суть поста и назначение.
Но с такой яростной критикой хабрапользователей уже сомневаюсь, что правильно поймут суть поста и назначение.
При 0 <= N <= const эффективны одни алгоритмы,
при const <= N <= inf — другие.
O(f(x)) введено для сравнения алгоритмов в рамках двух диапазонов.
при const <= N <= inf — другие.
O(f(x)) введено для сравнения алгоритмов в рамках двух диапазонов.
1. N
добавил UPD3 с исходниками
Последний раз о сложности:
UPD4.(23.12.2010 14:56) Насчет сложности O(N): предложенный алгоритм является разновидностью алгоритма сортировки подсчетом, имеющим линейную временную трудоёмкость Θ(n + k) © Wiki.
UPD4.(23.12.2010 14:56) Насчет сложности O(N): предложенный алгоритм является разновидностью алгоритма сортировки подсчетом, имеющим линейную временную трудоёмкость Θ(n + k) © Wiki.
Ограничение применимости:
Применение сортировки подсчётом целесообразно лишь тогда, когда сортируемые числа имеют (или их можно отобразить в) диапазон возможных значений, который достаточно мал по сравнению с сортируемым множеством, например, миллион натуральных чисел меньших 1000. Эффективность алгоритма падает, если при попадании нескольких различных элементов в одну ячейку, их надо дополнительно сортировать. Необходимость сортировки внутри ячеек лишает алгоритм смысла, так как каждый элемент придётся просматривать более одного раза.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Сортировка массива за O(N) на CUDA