Не такой уж ты и страшный, XTS-AES

Приветствую, %username%!

Сегодняшняя статья навеяна мыслями написать бесплатный аналог программы для шифрования файлов в DropBox, а именно аспектом режима шифрования файлов посекторно (для возможности читать\писать из/в произвольное место)
Мы поговорим о режиме шифрования XTS-AES, применяемом во всех популярных дискошифровалках (TrueCrypt, DiskCryptor).
Он описан в IEEE P1619™/D16 (Standard for Cryptographic Protection of Data on Block-Oriented Storage Devices) и считается самым безопасным способом хранить данные посекторно.


Перво-наперво определим входные данные для работы:

1. 256/512 бит ключа (может быть SHA-256/512(соль+пароль) или что нибудь вроде KDF)
2. Адрес (номер) сектора
3. Собсно блок данных длины кратной 128 битам (размер блока AES)

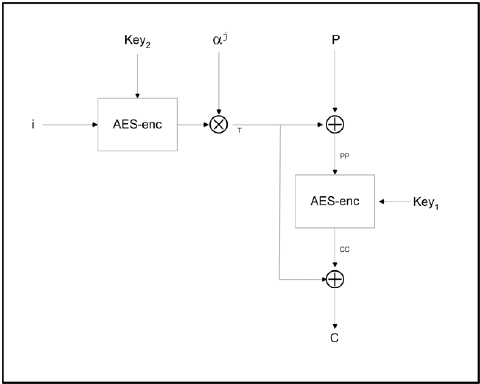
Упрощенно, алгоритм следующий:

1. Разбивка ключа на два. Первая часть становится ключом шифрования данных(k1), вторая — ключом для генерации tweak value(k2)
   Таким образом, если у нас используется ключ в 512 бит, то мы его пилим на 2х256 и используем в AES-256
2. Конвертируем номер сектора в массив байт и шифруем его ключом k2. Это наше tweak value
3. Идём по массиву данных блоками размером по 16 байт и для каждого блока:
4. 1.Ксорим его с tweak value
5. 2.Шифруем/расшифровываем его ключом k1
6. 3.Опять ксорим уже (рас)шифрованный блок данных с tweak value. Сохраняем его, это и будет нужный нам (за/рас)шифрованный блок сектора
7. 4.Умножаем tweak value на полином α = x¹²⁸+x⁷+x²+x+1

Самое непонятное тут (для меня, в частности) это умножение на полином. Алгоритмически это просто сдвиг всего массива на 1 бит + xor на последнем шаге.

1.  
2. private const int GF_128_FDBK = 0x87;
3. private const int AES_BLK_BYTES = 16;
4. ...
5.  
6. // умножаем T(weak value) на α
7. Cin = 0; // бит переноса
8. for (j = 0; j < AES_BLK_BYTES; j++)
9. {
10.     Cout = (T[j] >> 7) & 1;
11.     T[j] = (byte)(((T[j] << 1) + Cin) & 0xFF);
12.     Cin = Cout;
13. }
14. if (Cout != 0)
15. {
16.     T[0] ^= GF_128_FDBK;
17. }
18.  

В принципе, никакого криминала. Делается это для того, чтоб tweak value был различным для каждого блока данных внутри сектора.
Вопрос к математически подкованной аудитории: Почему выбрано именно умножение на полином в GF(2) по модулю x¹²⁸+x⁷+x²+x+1? Моих (не)знаний хватает лишь предположить, что тут замешаны циклические группы, и всё это некий аналог циклического сдвига.

Рабочий код на C#, который даже проходит стандартные тесты:

1.  
2. class XTS
3. {
4.     private const int GF_128_FDBK = 0x87;
5.     private const int AES_BLK_BYTES = 16;
6.  
7.     public static byte[] encryptSector(byte[] inData, byte[] dataEncryptionKey, byte[] tweakEncryptionKey, UInt64 sectorNumber, bool encrypt)
8.     {
9.         byte[] outData = new byte[inData.Length]; //тут будет результат. Размер inData должен быть кратен 32!
10.  
11.         uint i, j; // local counters
12.         var T = new byte[AES_BLK_BYTES]; // tweak value
13.         var x = new byte[AES_BLK_BYTES]; // буфер для (за/рас)шифрованного блока данных
14.  
15.         // конвертируем номер сектора в массив байт
16.         Array.Copy(BitConverter.GetBytes(sectorNumber), T, 8);
17.  
18.         //после шифрования в T у нас tweak value. true значит шифровать
19.         processAES(tweakEncryptionKey, T, true);
20.        
21.         // Обрабатываем по AES_BLK_BYTES байт за раз
22.         for (i = 0; i < inData.Length; i += AES_BLK_BYTES)
23.         {
24.             // ксорим tweak value с куском данных
25.             for (j = 0; j < AES_BLK_BYTES; j++)
26.             {
27.                 x[j] = (byte)(inData[i + j] ^ T[j]);
28.             }
29.  
30.             // шифруем/расшифровываем блок
31.             processAES(dataEncryptionKey, x, encrypt);
32.  
33.              // ксорим tweak value с обработанным блоком данных
34.             for (j = 0; j < AES_BLK_BYTES; j++)
35.             {
36.                 outData[i + j] = (byte)(x[j] ^ T[j]);
37.             }
38.  
39.             // Умножаем tweak value на α
40.             j = AES_BLK_BYTES;
41.             int t = T[AES_BLK_BYTES - 1];
42.             while (--j != 0)
43.                 T[j] = (byte)((T[j] << 1) | ((T[j - 1] & 0x80) != 0 ? 1 : 0));
44.             T[0] = (byte)((T[0] << 1) ^ ((t & 0x80) != 0 ? 0x87 : 0x00));
45.         }
46.         return outData;
47.     }
48.  
49.     private static void processAES(byte[] k, byte[] T, bool encrypt)
50.     {
51.         /*AesFastEngine взят из BouncyCastle. Вы можете заменить на стандартную
52.         * реализацию, либо вообще использовать другой алгоритм, только учитывайте
53.         * размер блока шифрования.
54.         */
55.         var engine = new AesFastEngine();
56.         engine.Init(encrypt, new KeyParameter(k));
57.         engine.ProcessBlock(T, 0, T, 0);
58.     }
59. }
60.  

______________________
Использовать AES, как видно, не обязательно. Правда, об этом ничего не сказано в стандарте.

Домашним заданием будет реализовать обработку сектора для размеров не кратных 32.
А я продолжу написание шифровалки для DropBox)