Рекурсивные функции — создание собственной математики (Scala)

Добрый день, Хабр!

Столь претензионным заголовком я хочу начать статью про одну из многих моделей исчисления (Computational model) — рекурсивные функции. В первой части этого поста мы разберем (в кратце, ибо подробно все расписано на Википедии) теоретическую составляющую этой модели (примитивная рекурсия), во второй же половине мы попробуем претворить данную модель в жизнь (частично) с помощью языка Scala.

1. Рекурсивные функции — что это?

Всем известно словосочетание «Машина Тьюринга» — модель исчисления, созданная британским математиком, логиком, криптографом и просто хорошим человеком Аланом Тьюрингом. Данная модель является одной из самых известных и популярных моделей исчисления среди многих. Однако, с недавнего времени начали популяризироваться другие модели, такие как лябмда-исчисления и мю-рекурсия.

И всё же, что такое рекурсивная функция?
Представте себе, что перед вами лежит абстрактная вычислительная машина, которая не знает (пока еще) таких операций как сложение двух чисел, вычитание, дифференцирование и интегрирование. Как работать с такой машиной? Как научить ее считать?
Для начала, определим базовый функционал, которым должна обладать данная машина:

• Набор базовых математических функций:
  
  — Zero(x)=0: для каждого данного аргумента x функция возвращает 0
  
  — Succ(x)=x+1: для каждого данного x функция возвращает x+1
  
  — Семейство функций проекций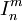 , где 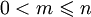: для любых n аргументов возвращает тот, которые стоит на m позиции.
  
• Набор операций, которые мы можем применить на данные функции:
  
  — Композиция функций (суперпо��иция): (f•g)(x)=f(g(x));
  
  — Примитивная рекурсия: Пусть есть функция f(x1,x2,...,xn) от n переменных, и функция g(X1,X2,...,Xn,Xn+1,Xn+2) от n+2 переменных. Тогда мы можем задать функцию h(X1,X2,....Xn,Xn+1) от n+1 переменных:
  
  h(X1,X2,...,Xn,0) = f(X1,X2,...,Xn);
  h(X1,X2,...,Xn,i+1) = g(X1,X2,...,Xn, i, h(X1,X2,...,Xn,i));
  

Вот собственно и все, что может делать наша абстрактная вычислительная машина. Главное в этом списке, как вы уже догадались, это примитивная рекурсия. Что бы было понятней, поставим себе задачу, например, реализовать функцию сложения двух чисел a и b:

Sum(a,b):
Sum(a,0) = I(a);
Sum(a,i+1) = Succ(F(a,i,Sum(a,i))) где F — проекция третьего аргумента, то есть в данном случае F вернет Sum(a,i);

Все! Теперь мы умеем складывать два числа и мы этому очень рады.
Кстати, возможно у кого-то возник вопрос, зачем так сложно расписывать Sum(a, i+1), и почему не написать просто Sum(a, i+1)=Succ(Sum(a,i)). Отвечаю: по определению, рекурсивная функция должна иметь как аргументы все аргументы (кроме итерационного) желаемой функции (в нашем случае это a), также итерационный аргумент, уменьшенный на единицу (в нашем случае это i), и собственно сам рекурсивный вызов Sum(a,i). Сделано это для возможности работать с непримитивной рекурсией (итерация идет по двум и больше аргументам).

Как вы понимаете, таким же методом мы можем создать функцию уможения, степени, и т.д. Все эти примеры очень хорошо расписаны на Википедии, да и мы их реализуем во второй части статьи. В любом случае, мы можем уже определить бесконечное множество примитивно-рекурсивных функций:

F={f0, f1, f2, f3, ...} — бесконечное исчисляемое множество функций, заданных следующим образом:

f0(0,y) = Succ(y);
f[n+1](x,y): f[n+1](0,y)=y; f[n+1](i+1,y)=fn(y, f[n+1](i,y));

Вот это и есть примитивная рекурсия.
Я не буду погружаться глубже и рассказывать, что такое μ-recursive function, на википедии все очень приятно расписано, тем более что примитивной рекурсии нам достаточно для начала реализации собственной… математики!

2.Примитивная рекурсия на Scala

Для начала, нам надо определить, что такое число? Создадим абстрактный класс MyNumber:

abstract class MyNumber {

  val isNatural: Boolean
  val isNeg: Boolean
  val isZero: Boolean
  val isInf: Boolean
  
  def +(b: MyNumber): MyNumber
  def -(b: MyNumber): MyNumber
  def *(b: MyNumber): MyNumber
  def /(b: MyNumber): MyNumber
  def ^(b: MyNumber): MyNumber
  def <(b: MyNumber): Boolean
  def >(b: MyNumber): Boolean
  def ==(b: MyNumber): Boolean
  def neg: MyNumber
  def abs: MyNumber
  
  def pre: MyInteger
  def suc: MyInteger
  val num: MyInteger
  val denum: MyInteger
  
  def gcd(b: MyNumber): MyNumber  
  def mod(b: MyInteger): MyNumber
  override def toString(): String
  
  def toInteger: MyInteger =
    if(isNatural) this.asInstanceOf[MyInteger]
    else (num / denum).asInstanceOf[MyInteger]
  
  def toFraction: Fraction = 
    if(isNatural) new Fraction(this.toInteger)
    else this.asInstanceOf[Fraction]
}

Как уже видно, у нас будут два дочерних класса, Fraction и MyInteger:

abstract class MyInteger extends MyNumber {
  val isNatural = true
  val isNeg: Boolean
  val isZero: Boolean
  val isInf: Boolean
  
  def +(b: MyNumber): MyNumber =
    if (b.isNatural) this plusInt b.toInteger
    else this plusFrac b.toFraction

  protected def plusInt(b: MyInteger): MyNumber
  private def plusFrac(b: Fraction): MyNumber = this.toFraction + b

  def -(b: MyNumber): MyNumber =
    if (b.isNatural) this minusInt b.toInteger
    else this minusFrac b.toFraction

  protected def minusInt(b: MyInteger): MyNumber
  private def minusFrac(b: Fraction): MyNumber = this.toFraction - b

  def *(b: MyNumber): MyNumber =
    if (b.isNatural) this multInt b.toInteger
    else this multFrac b.toFraction

  protected def multInt(b: MyInteger): MyNumber
  private def multFrac(b: Fraction): MyNumber = this.toFraction * b

  def /(b: MyNumber): MyNumber =
    if (b.isNatural) this divInt b.toInteger
    else this divFrac b.toFraction

  protected def divInt(b: MyInteger): MyNumber
  private def divFrac(b: Fraction): MyNumber = this.toFraction / b

  def ^(b: MyNumber): MyNumber =
    if (b.isNatural) this powInt b.toInteger
    else this powFrac b.toFraction

  protected def powInt(b: MyInteger): MyNumber
  protected def powFrac(b: Fraction): MyNumber //TODO

  def <(b: MyNumber): Boolean =
    if (b.isNatural) this lessThanInt b.toInteger
    else this lessThanFrac b.toFraction

  protected def lessThanInt(b: MyInteger): Boolean
  private def lessThanFrac(b: Fraction): Boolean = this.toFraction < b

  def >(b: MyNumber): Boolean =
    if (b.isNatural) this biggerThanInt b.toInteger
    else this biggerThanFrac b.toFraction

  protected def biggerThanInt(b: MyInteger): Boolean
  private def biggerThanFrac(b: Fraction): Boolean = this.toFraction > b

  def ==(b: MyNumber): Boolean =
    if (b.isNatural) this equalsInt b.toInteger
    else this equalsFrac b.toFraction

  protected def equalsInt(b: MyInteger): Boolean
  private def equalsFrac(b: Fraction): Boolean = this.toFraction == b

  def pre: MyInteger
  def suc: MyInteger
  val num: MyInteger = null
  val denum: MyInteger = null

  def neg: MyNumber

  def abs: MyNumber =
    if (!isNeg || isZero) this
    else this neg

  def gcd(b: MyNumber): MyNumber =
    if (b.isNatural) this gcdPrivate b.abs.toInteger
    else (new Zero).pre

  private def gcdPrivate(b: MyNumber): MyNumber = {
      def iter(a: MyNumber, b: MyNumber): MyNumber = {
        if (b == (new Zero)) a else iter(b, a.toInteger mod b.toInteger)
      }
    iter(this, b)
  }
  def mod(b: MyInteger): MyNumber = {
      def iter(a: MyNumber, b: MyNumber): MyNumber = {
        if (b.isNeg) this mod b.abs.toInteger
        else if (!b.isNatural) (new Zero).pre
        else if (a < b) if (a.isNeg) a + b else a
        else iter(if (a.isNeg) a + b else a - b, b)
      }
    iter(this, b)
  }

  override def toString: String = {
      def iter(nb: MyInteger, accu: Int): Int = {
        if (nb isZero) accu
        else if (nb isNeg) iter(nb.suc.toInteger, accu - 1)
        else iter(nb.pre.toInteger, accu + 1)
      }
    if(this.isInf) "Inf" else iter(this, 0).toString()
  }
}

Для определения Integer'а, нам понадобится понятие следующего числа (Suc), предыдущего (Pre), нуля (Zero) и бесконечности (PosInf):

class Zero extends MyInteger {
  val isZero = true
  val isNeg = false
  val isInf = false
  
  protected def plusInt(b: MyInteger): MyNumber = b
  protected def minusInt(b: MyInteger): MyNumber = b neg
  protected def multInt(b: MyInteger): MyNumber = this
  protected def divInt(b: MyInteger): MyNumber =
    if (b.isZero) new PosInf
    else if(b.isInf) new Zero
    else this
  protected def powInt(b: MyInteger): MyNumber = this.suc
  protected def powFrac(b: Fraction): MyNumber = this.suc
  protected def lessThanInt(b: MyInteger): Boolean = !b.isNeg && !b.isZero
  protected def biggerThanInt(b: MyInteger): Boolean = b.isNeg && !b.isZero
  protected def equalsInt(b: MyInteger): Boolean = b.isZero

  def pre: MyInteger = new Pre(this)
  def suc: MyInteger = new Suc(this)

  def neg = this
}

class PosInf extends MyInteger {
  val isZero = false
  val isNeg = false
  val isInf = true
  
  protected def plusInt(b: MyInteger): MyNumber = this
  protected def minusInt(b: MyInteger): MyNumber = this
  protected def multInt(b: MyInteger): MyNumber = this
  protected def divInt(b: MyInteger): MyNumber = this
  protected def powInt(b: MyInteger): MyNumber = this
  protected def powFrac(b: Fraction): MyNumber = this
  protected def lessThanInt(b: MyInteger): Boolean = false
  protected def biggerThanInt(b: MyInteger): Boolean = true
  protected def equalsInt(b: MyInteger): Boolean = b.isInf

  def pre: MyInteger = this
  def suc: MyInteger = this

  def neg = this
}

class Pre(nb: MyInteger) extends MyInteger {
  val isZero = false
  val isNeg = true
  val isInf = false
  
  protected def plusInt(b: MyInteger): MyNumber = {
      def iter(b: MyInteger, accu: MyNumber): MyNumber = {
        if (b isNeg) this - (b neg)
        else if (b isZero) accu
        else iter(b.pre, accu.suc)
      }
    iter(b, this)
  }

  protected def minusInt(b: MyInteger): MyNumber = {
      def iter(b: MyInteger, accu: MyNumber): MyNumber = {
        if (b isNeg) (this + (b neg))
        else if (b isZero) accu
        else iter(b.pre, accu.pre)
      }
    iter(b, this)
  }

  protected def multInt(b: MyInteger): MyNumber = {
    (this.neg * b).neg
  }

  protected def divInt(b: MyInteger): MyNumber =
    if (b.isZero) new PosInf
    else if(b.isInf) new Zero
    else if (b.isNeg) this.abs / b.abs
    else (this.abs / b).neg

  protected def powInt(b: MyInteger): MyNumber = if(b!=new Zero)(this.neg ^ b).neg else (new Zero).suc

  protected def powFrac(b: Fraction): MyNumber = (new Zero).pre //TODO

  protected def lessThanInt(b: MyInteger): Boolean = {
      def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match {
        case true  => !(a isZero) && (b isZero)
        case false => iter(a.suc, b.suc)
      }
    if (!b.isNeg || b.isZero) true else iter(this, b)
  }

  protected def biggerThanInt(b: MyInteger): Boolean = {
      def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match {
        case true  => (a isZero) && !(b isZero)
        case false => iter(a.suc, b.suc)
      }
    if (!b.isNeg || b.isZero) false else iter(this, b)
  }
  protected def equalsInt(b: MyInteger): Boolean = !(this < b) && !(this > b)

  def pre: MyInteger = new Pre(this)
  def suc: MyInteger = nb

  def neg = {
      def iter(nb: MyInteger, accu: MyInteger): MyInteger = {
        if (nb isZero) accu
        else iter(nb.suc, accu.suc)
      }
    iter(this, new Zero)
  }
}

class Suc(nb: MyInteger) extends MyInteger {

  val isZero = false
  val isNeg = false
  val isInf = false
  
  protected def plusInt(b: MyInteger): MyNumber = {
      def iter(b: MyInteger, accu: MyNumber): MyNumber = {
        if (b isNeg) this - (b neg)
        else if (b isZero) accu
        else iter(b.pre, accu.suc)
      }
    iter(this, b)
  }

  protected def minusInt(b: MyInteger): MyNumber = {
      def iter(b: MyInteger, accu: MyNumber): MyNumber = {
        if (b isNeg) this + (b neg)
        else if (b isZero) accu
        else iter(b.pre, accu.pre)
      }
    iter(b, this)
  }

  protected def multInt(b: MyInteger): MyNumber = {
      def iter(a: MyInteger, b: MyInteger, accu: MyNumber): MyNumber = {
        if (b.isZero) accu
        else iter(a, b.pre, accu + a)
      }
    if (b.isZero) new Zero
    else {
      if (this < b) {
        if (b.isNeg) iter(b.neg.toInteger, this, new Zero).neg
        else iter(b, this, new Zero)
      } else {
        if (b.isNeg) iter(this, b.neg.toInteger, new Zero).neg
        else iter(this, b, new Zero)
      }
    }
  }

  protected def divInt(b: MyInteger): MyNumber = {
      def iter(a: MyNumber, b: MyNumber, count: MyNumber): MyNumber = {
        if (a.isZero) count
        else if (a.isNeg) count.pre
        else iter(a - b, b, count.suc)
      }

    if (b.isZero) new PosInf
    else if(b.isInf) new Zero
    else if (b.isNeg) iter(this, b.abs, new Zero).neg
    else iter(this, b, new Zero)
  }

  protected def powInt(b: MyInteger): MyNumber = {
      def iter(a: MyInteger, b: MyInteger, accu: MyNumber): MyNumber = {
        if (b.isZero) accu
        else iter(a, b.pre, accu * a)
      }
    if (b.isZero) (new Zero).suc
    else {
      if (b.isNeg) new Fraction((new Zero).suc, iter(this, b.neg.toInteger, (new Zero).suc).toInteger)
      else new Fraction(iter(b, this, (new Zero).suc).toInteger)
    }
  }

  protected def powFrac(b: Fraction): MyNumber = (new Zero).pre //TODO

  protected def lessThanInt(b: MyInteger): Boolean = {
      def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match {
        case true  => (a isZero) && !(b isZero)
        case false => iter(a.pre, b.pre)
      }
    if (b.isNeg || b.isZero) false else iter(this, b)
  }

  protected def biggerThanInt(b: MyInteger): Boolean = {
      def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match {
        case true  => !(a isZero) && (b isZero)
        case false => iter(a.pre, b.pre)
      }
    if (b.isNeg || b.isZero) true else iter(this, b)
  }
  protected def equalsInt(b: MyInteger): Boolean = !(this < b) && !(this > b)

  def pre: MyInteger = nb
  def suc: MyInteger = new Suc(this)

  def neg = {
      def iter(nb: MyInteger, accu: MyInteger): MyInteger = {
        if (nb isZero) accu
        else iter(nb.pre, accu.pre)
      }
    iter(this, new Zero)
  }
}

Класс Fraction несколько легче, ибо он полностью базируется на MyInteger:

class Fraction(x: MyInteger, y: MyInteger) extends MyNumber {
  def this(x: MyInteger) = this(x, (new Zero).suc)

  val isNatural: Boolean = false
  val isNeg: Boolean = (x.isNeg && !y.isNeg) || (!x.isNeg && y.isNeg)
  val isZero: Boolean = x.isZero
  val isInf: Boolean = x.isInf || y.isInf
  
  def +(b: MyNumber): MyNumber = this plus b.toFraction
  private def plus(b: Fraction): MyNumber = new Fraction((this.num * b.denum + this.denum * b.num).toInteger, (this.denum * b.denum).toInteger)

  def -(b: MyNumber): MyNumber = this minus b.toFraction
  private def minus(b: Fraction): MyNumber = new Fraction((this.num * b.denum - this.denum * b.num).toInteger, (this.denum * b.denum).toInteger)

  def *(b: MyNumber): MyNumber = this mult b.toFraction
  private def mult(b: Fraction): MyNumber = new Fraction((this.num * b.num).toInteger, (this.denum * b.denum).toInteger)

  def /(b: MyNumber): MyNumber = this div b.toFraction
  private def div(b: Fraction): MyNumber = new Fraction((this.num * b.denum).toInteger, (this.denum * b.num).toInteger)

  def ^(b: MyNumber): MyNumber =
    if (!b.isNatural) (new Zero).pre
    else new Fraction((this.num ^ b.toInteger).toInteger, (this.denum ^ b.toInteger).toInteger)

  def <(b: MyNumber): Boolean =
    if (this.num.isNeg) {
      if (b.num.isNeg) this.neg > b.neg
      else true
    } else if (this.isZero) {
      if (b.isZero || b.num.isNeg) false
      else true
    } else {
      if (b.num.isNeg || b.isZero) false
      else this.num * b.denum < this.denum * b.num
    }
  
  def >(b: MyNumber): Boolean =
    if(this.num.isNeg){
      if(b.num.isNeg) this.neg < b.neg
      else false
    }else if(this.isZero){
      if(b.isZero || !b.num.isNeg) false
      else true
    }else{
      if(b.num.isNeg || b.isZero) true
      else this.num * b.denum > this.denum * b.num
    }
  
  def ==(b: MyNumber): Boolean =
    if(!b.isNatural)(this.num == b.num) && (this.denum == b.denum)
    else this == b.toFraction
  
  def neg: MyNumber = new Fraction(num.neg.toInteger, denum)
  def abs: MyNumber = new Fraction(num.abs.toInteger, denum)

  def pre: MyInteger = sys.error("Predicat of fraction")
  def suc: MyInteger = sys.error("Successor of fraction")
  
  val num = ((if(this.isNeg)x.abs.neg else x.abs) / (x.abs gcd y.abs)).toInteger
  val denum = (y.abs / (x.abs gcd y.abs)).toInteger
  
  def gcd(b: MyNumber): MyNumber = this.denum gcd (new Zero).suc
  def mod(b: MyInteger): MyNumber = new Zero
  
  override def toString(): String =
    if(num.isZero) 0.toString()
    else if(this.isInf) "вИЮ"
    else if(denum == (new Zero).suc) num.toString()
    else num + "/" + denum
}

Вот и все! У нас теперь есть натуральные и дробные числа, и набор простейших операций (заметьте, ни единого использования нативных классов!)

По такому же принципу можно создавать структуры данных для новоявленных чисел:

abstract class MySet {

  def add(elem: MyNumber): MySet
  def delete(elem: MyNumber): MySet
  def union(set: MySet): MySet
  def intersec(set: MySet): MySet
  def contains(elem: MyNumber): Boolean
  def linearSearch(elem: MyNumber): MySet
  def mergeSort: MySet
  def merge: MySet
  def quickSort: MySet
  def timSort: MySet
  def binaryTreeSort: MySet
  def length: MyNumber
  def get(pos: MyNumber): MyNumber
  def take(n: MyNumber): MySet
  def drop(n: MyNumber): MySet
  
  def map(p: MyNumber => MyNumber): MySet
  def filter(p: MyNumber => Boolean): MySet
  def flat(p: (MyNumber, MyNumber) => MyNumber): MyNumber

Да и много чего можно сделать с рекурсивными функциями, даже создать свою вселенную. «С блекджеком и шлюхами». Спасибо за внимание.