Не знаю, как вы, уважаемый читатель, а я всегда поражался контрасту между изяществом базовой идеи, заложенной в концепцию двоичных деревьев поиска, и сложностью реализации сбалансированных двоичных деревьев поиска (красно-черные деревья, АВЛ-деревья, декартовы деревья). Недавно, перелистывая в очередной раз Седжвика [1], нашел описание рандомизированных деревьев поиска (нашлась и оригинальная работа [2]) — настолько простое, что занимает оно всего треть страницы (вставка узлов, еще страница — удаление узлов). Кроме того, при ближайшем рассмотрении обнаружился дополнительный бонус в виде очень красивой реализации операции удаления узлов из дерева поиска. Далее вы найдете описание (с цветными картинками) рандомизированных деревьев поиска, реализация на С++, а также результаты небольшого авторского исследования сбалансированности описываемых деревьев.
Начнем помаленьку
Поскольку я собираюсь описать полную реализацию дерева, то придется начать с начала (профессионалы могут спокойно пропустить пару-другую разделов). Каждый узел двоичного дерева поиска будет содержать ключ key, который по сути управляет всеми процессами (у нас он будет целым), и пару указателей left и right на левое и правое поддеревья. Если какой-либо указатель нулевой, то соответствующее дерево является пустым (т.е. попросту отсутствует). Помимо этого, нам для реализации рандомизированного дерева потребуется еще одно поле size, в котором будет храниться размер (в
struct node // структура для представления узлов дерева
{
int key;
int size;
node* left;
node* right;
node(int k) { key = k; left = right = 0; size = 1; }
};
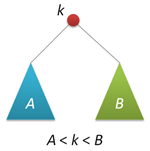Основное свойство дерева поиска — любой ключ в левом поддереве меньше корневого ключа, а в правом поддереве — больше корневого ключа (для ясности изложения будем считать, что все ключи различны). Это свойство (схематически показанное на рисунке справа) позволяет нам очень просто организовать поиск заданного ключа, перемещаясь от корня вправо или влево в зависимости от значения корневого ключа. Рекурсивный вариант фунции поиска (а мы будем рассматривать только такие) выглядит следующим образом: node* find(node* p, int k) // поиск ключа k в дереве p
{
if( !p ) return 0; // в пустом дереве можно не искать
if( k == p->key )
return p;
if( k < p->key )
return find(p->left,k);
else
return find(p->right,k);
}
Переходим к вставке новых ключей в дерево. В классическом варианте вставка повторяет поиск с тем отличием, что когда мы упираемся в пустой указатель, мы создаем новый узел и подвешиваем его к тому месту, где мы обнаружили тупик. Сначала я не хотел расписывать эту функцию, потому что в рандомизированном случае она работает немного по-другому, но передумал, т.к. хочу зафиксировать пару моментов.
node* insert(node* p, int k) // классическая вставка нового узла с ключом k в дерево p
{
if( !p ) return new node(k);
if( p->key>k )
p->left = insert(p->left,k);
else
p->right = insert(p->right,k);
fixsize(p);
return p;
}
Во-первых, любая функция, которая модифицирует заданное дерево, возвращает указатель на новый корень (неважно, изменился он или нет), а дальше вызывающая функция сама решает, куда подвешивать это дерево. Во-вторых, т.к. мы вынуждены хранить размер дерева, то при любом изменении поддеревьев нужно корректировать размер самого дерева. Этим у нас будет заниматься следующая пара функций:
int getsize(node* p) // обертка для поля size, работает с пустыми деревьями (t=NULL)
{
if( !p ) return 0;
return p->size;
}
void fixsize(node* p) // установление корректного размера дерева
{
p->size = getsize(p->left)+getsize(p->right)+1;
}
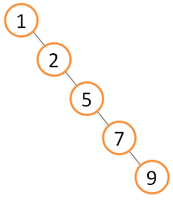Что же не так в функции insert? Проблема заключается в том, что эта функция не гарантирует сбалансированности получаемого дерева, например, если ключи будут подаваться в порядке возрастания, то дерево выродится в односвязный список (см. рисунок) со всеми сопутствующими «плюшками», главный из которых — это линейное время выполнения всех операций над таким деревом (в то время, как для сбалансированных деревьев это время является логарифмическим). Существуют разные способы избежать несбалансированности. Условно их можно разделить на два класса, те которые гарантируют сбалансированность (красно-черные деревья, АВЛ-деревья), и те которые обеспечивают ее в вероятностном смысле (декартовы деревья) — вероятность получения несбарансированного дерева при этом оказывается пренебрежимо малой при больших размерах деревьев. Я думаю, не будет сюрпризом, если я скажу, что рандомизированные деревья относятся как раз ко второму классу. Вставка в корень дерева
Необходимой составляющей рандомизации является применение специальной вставки нового ключа, в результате которой новый ключ оказывается в корне дерева (полезная функция во многих отношениях, т.к. доступ к недавно вставленным ключам оказывается в результате очень быстрым, привет самоорганизующимся спискам). Для реализации вставки в корень нам потребуется функция поворота, которая производит локальное преобразование дерева.
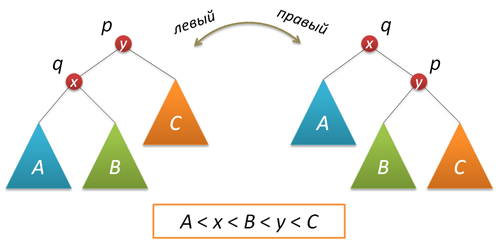
Не забываем скорректировать размеры поддеревьев и вернуть корень нового дерева:
node* rotateright(node* p) // правый поворот вокруг узла p
{
node* q = p->left;
if( !q ) return p;
p->left = q->right;
q->right = p;
q->size = p->size;
fixsize(p);
return q;
}
node* rotateleft(node* q) // левый поворот вокруг узла q
{
node* p = q->right;
if( !p ) return q;
q->right = p->left;
p->left = q;
p->size = q->size;
fixsize(q);
return p;
}
Теперь собственно вставка в корень. Сначала рекурсивно вставляем новый ключ в корень левого или правого поддеревьев (в зависимости от результата сравнения с корневым ключом) и выполняем правый (левый) поворот, который поднимает нужный нам узел в корень дерева.
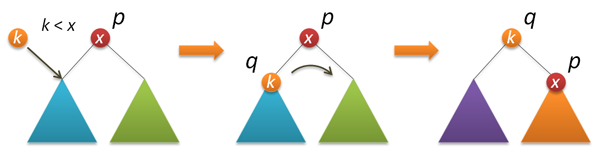
node* insertroot(node* p, int k) // вставка нового узла с ключом k в корень дерева p
{
if( !p ) return new node(k);
if( k<p->key )
{
p->left = insertroot(p->left,k);
return rotateright(p);
}
else
{
p->right = insertroot(p->right,k);
return rotateleft(p);
}
}
Рандомизированная вставка
Вот мы и добрались до рандомизации. На сей момент у нас имеется две функции вставки — простая и в корень, из них мы сейчас и скомбинируем рандомизированную вставку. Смысл всего этого заключается в следующей идее. Известно, что если заранее перемешать как следует все ключи и потом построить из них дерево (ключи вставляются по стандартной схеме в полученном после перемешивания порядке), то построенное дерево окажется неплохо сбалансированным (его высота будет порядка 2log2n против log2n для идеально сбалансированного дерева). Заметим, что в этом случае корнем может с одинаковой вероятностью оказаться любой из исходных ключей. Что делать, если мы заранее не знаем, какие у нас будут ключи (например, они вводятся в систему в процессе использования дерева)? На самом деле все просто. Раз любой ключ (в том числе и тот, который мы сейчас должны вставить в дерево) может оказаться корнем с вероятностью 1/(n+1) (n — размер дерева до вставки), то мы выполняем с указанной вероятностью вставку в корень, а с вероятностью 1-1/(n+1) — рекурсивную вставку в правое или левое поддерево в зависимости от значения ключа в корне:
node* insert(node* p, int k) // рандомизированная вставка нового узла с ключом k в дерево p
{
if( !p ) return new node(k);
if( rand()%(p->size+1)==0 )
return insertroot(p,k);
if( p->key>k )
p->left = insert(p->left,k);
else
p->right = insert(p->right,k);
fixsize(p);
return p;
}
Вот и вся хитрость… Проверим, как все это работает. Пример построения дерева из 500 узлов (на вход поступали ключи от 0 до 499 в порядке возрастания):
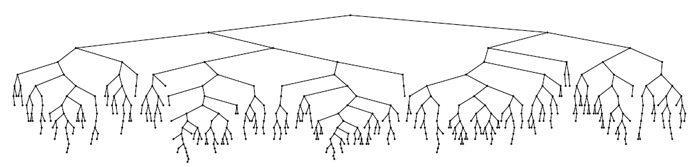Не сказать, что идеал красоты, но высота явно небольшая. Усложним задачу — будем строить дерево, подавая на вход ключи от 0 до 214-1 (идеальная высота равна 14), и измерять высоту в процессе построения. Для надежности сделаем тысячу прогонов и усредним результат. Получаем следующий график, на котором маркерами отмечены наши результаты, а сплошной линией — теоретическая оценка из [3] — h=4.3ln(n)-1.9ln(ln(n))-4. Самое главное, что мы видим из рисунка — это то, что теория вероятностей — это сила!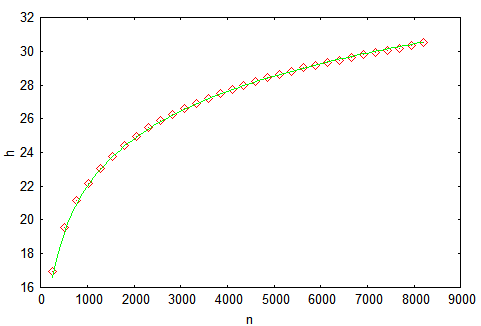 
Следует понимать, что на предложенном графике показано среднее значение высоты дерева по большому числу расчетов. А насколько может отличаться высота в одном конкретном расчете. В указанной выше статье есть ответ и на этот вопрос. Мы же поступим по рабоче-крестьянски и построим гистограмму распределения высот после вставки 4095 узлов.
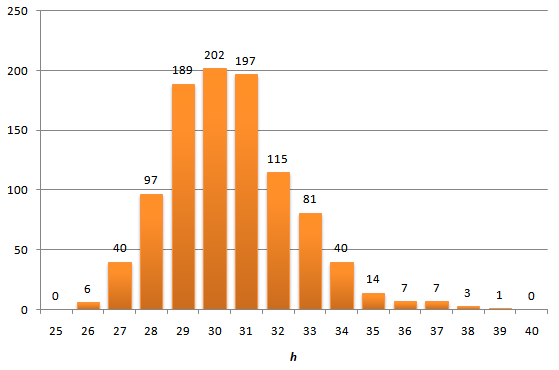
В общем, никакого криминала не видно, хвосты распределения короткие — максимальная полученная высота равна 39, что не сильно превышает среднее
Удаление ключей
Итак, у нас есть сбалансированное (хоть в каком-то смысле) дерево. Правда, пока оно не поддерживает удаление узлов. Этим мы теперь и займемся. Тот вариант удаления, который прописывается во многих учебниках и который хорошо (с картинками) описан на хабре, может и работает быстро, но выглядит очень уж непрезантабельно (по сравнению со вставкой). Мы пойдем другим путем, примерно так, как это было показано в этом замечательном посте (на мой взгляд — это лучшее описание декартовых деревьев). Прежде чем удалять узлы, научимся соединять деревья. Пусть даны два дерева поиска с корнями p и q, причем любой ключ первого дерева меньше любого ключа во втором дереве. Требуется объединить эти два дерева в одно. В качестве корня нового дерева можно взять любой из двух корней, пусть это будет p. Тогда левое поддерево p можно оставить как есть, а справа к p подвесить объединение двух деревьев — правого поддерева p и всего дерева q (они удовлетворяют всем условиям задачи).
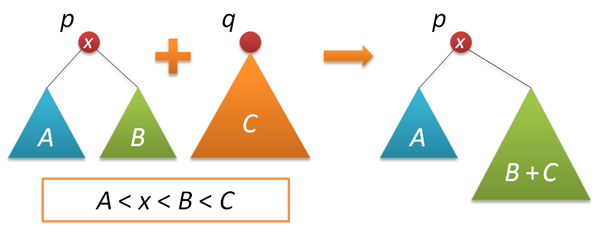
С другой стороны, с тем же успехом мы можем сделать корнем нового дерева узел q. В рандомизированной реализации выбор между этими альтернативами делается случайным образом. Пусть размер левого дерева равен n, правого — m. Тогда p выбирается новым корнем с вероятностью n/(n+m), а q — с вероятностью m/(n+m).
node* join(node* p, node* q) // объединение двух деревьев
{
if( !p ) return q;
if( !q ) return p;
if( rand()%(p->size+q->size) < p->size )
{
p->right = join(p->right,q);
fixsize(p);
return p;
}
else
{
q->left = join(p,q->left);
fixsize(q);
return q;
}
}
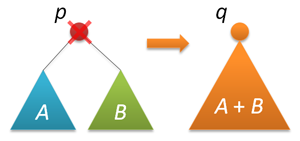Теперь все готово для удаления. Удалять мы будем по ключу — ищем узел с заданным ключом (напомню, что у нас все ключи различны) и удаляем этот узел из дерева. Стадия поиска такая же как и при поиске (как это ни странно), а вот дальше делаем так — объединяем левое и правое поддеревья найденного узла, удаляем узел, возвращаем корень объединенного дерева.node* remove(node* p, int k) // удаление из дерева p первого найденного узла с ключом k
{
if( !p ) return p;
if( p->key==k )
{
node* q = join(p->left,p->right);
delete p;
return q;
}
else if( k<p->key )
p->left = remove(p->left,k);
else
p->right = remove(p->right,k);
return p;
}
Проверим, что удаление не нарушает сбалансированности дерева. Для этого построим дерево с 215 ключами, потом удалим половину (со значениями от 0 до 214-1) и посмотрим на распределение высот…
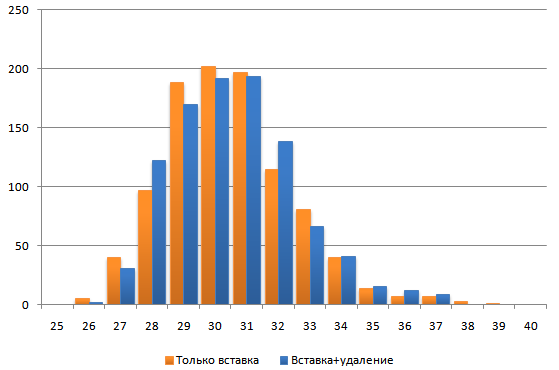
Практически никакого отличия, что и требовалось «доказать»…
Вместо заключения
Несомненное достоинство рандомизированных двоичных деревьев поиска — это простота и красота их реализации. Однако, как известно бесплатных пирожных не бывает. Чем мы же платим в данном случае? Во-первых, дополнительной памятью для хранения размеров поддеревьев. Одно целочисленное поле на каждый узел. В красно-черных деревьях при некоторой сноровке можно обойтись вообще без дополнительных полей. С другой стороны, размер дерева не совсем бесполезная информация, потому что он позволяет организовать доступ к данным по номеру (задача выборки или поиск порядковых статистик), что превращает наше дерево, по сути, в упорядоченный массив с возможностью вставки и удаления любых элементов. Во-вторых, время работы хотя и логарифмическое, но я подозреваю, что константа пропорциональности будет немаленькой — почти все операции выполняются в два прохода (и вниз и вверх), кроме того, вставка и удаление требуют случайных чисел. Есть и хорошая новость — на стадии поиска все должно работать очень быстро. Наконец, принципиальное препятствие для использования таких деревьев в серьезных приложениях — это то, что не гарантируется логарифмическое время, всегда есть шанс, что дерево окажется плохо сбалансированным. Правда, вероятность такого события уже при десятке тысяч узлов является настолько малой, что, пожалуй, можно и рискнуть…
Спасибо за внимание!
Литература
- Роберт Седжвик, Алгоритмы на C++, М.: Вильямс, 2011 г. — просто хорошая книга
- Martinez, Conrado; Roura, Salvador (1998), Randomized binary search trees, Journal of the ACM (ACM Press) 45 (2): 288–323 — оригинальная статья
- Reed, Bruce (2003), The height of a random binary search tree, Journal of the ACM 50 (3): 306–332 — оценка высоты дерева
