Добрый вечер, Хабр.
Эта статья для новичков, расскажу об отрисовке простых тел вращения в Windows Presentation Foundation. После семестра программирования графики на OpenGL, а точнее glut.h, решил потратить вечер на знакомство с WPF.В данной статье построим тор.
Основным строительным блоком в WPF является mesh, перевода термина на русский я не нашел, но думаю можно перевести как треугольный сегмент или просто треугольник. Возникает вопрос: почему треугольник, а не линия?
Пусть нам нужно построить базовое представление поверхности — плоскость. Как известно из школьной геометрии плоскость строится как минимум на трех точках и вполне логично составлять поверхности из треугольников.
С каждым треугольным сегментом связанны такие характеристики, как положение его вершин и нормаль. Вершины перечисляются по часовой стрелке или против, в зависимости от того какая из плоскостей треугольника (которых две), должна быть видима. Определяется нужный порядок очень просто, достаточно воспользоваться
Нормаль — это вектор перпендикулярный к плоскости треугольника определяется как
Добавляются нормали в той же последовательности, что и вершины.
В итоге у каждого треугольного сегмента есть
Начало системы координат при работе с 3D графикой находится в в центре сцены, в отличии от 2D, где начало в левом верхнем углу. Отображает графическое содержание сцены класс Viewport3D

Так как представление 3D объектов на экране это фактически двумерные проекции, то следует выбрать точку наблюдения, от которой и будет зависеть вид объекта. В WPF эту точку помогает указать класс camera
Тор — это поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности.
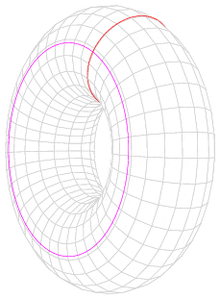
Уравнения тора можно представить в параметрическом и алгебраическом виде, в данном случае удобнее пользоваться
параметрическим.
x = (R + r * cos(a)) * cos(b)
y = r * sin (a)
z = -(R + r * cos(a))sin(b)
Закодируем уравнение тора.
Данный метод просто возвращает точку по заданным радиусам и углам:
Создадим метод построения треугольного сегмента
Все готово для отрисовки тора.
Строим сегменты представленные на рисунке выше, каждый из которых является объединением двух треугольников построенных на четырех вершинах.
Остается вызвать метод отрисовки тора
Графический интерфейс делается с XAML очень быстро, приведу лишь добавление ViewPort3D
Вот, что получилось в итоге:

И удалим несколько сегментов

Спасибо за внимание.
Эта статья для новичков, расскажу об отрисовке простых тел вращения в Windows Presentation Foundation. После семестра программирования графики на OpenGL, а точнее glut.h, решил потратить вечер на знакомство с WPF.В данной статье построим тор.
Основы WPF
Основным строительным блоком в WPF является mesh, перевода термина на русский я не нашел, но думаю можно перевести как треугольный сегмент или просто треугольник. Возникает вопрос: почему треугольник, а не линия?
Пусть нам нужно построить базовое представление поверхности — плоскость. Как известно из школьной геометрии плоскость строится как минимум на трех точках и вполне логично составлять поверхности из треугольников.
Для примера я удалил несколько строительных блоков из цилиндра

С каждым треугольным сегментом связанны такие характеристики, как положение его вершин и нормаль. Вершины перечисляются по часовой стрелке или против, в зависимости от того какая из плоскостей треугольника (которых две), должна быть видима. Определяется нужный порядок очень просто, достаточно воспользоваться
правилом правой руки
Поднимите большой палец правой руки, он обозначает сторону на которую вы смотрите. Опустите палец вниз, увидите противоположную, положение остальных пальцев покажет порядок обхода.


Нормаль — это вектор перпендикулярный к плоскости треугольника определяется как
векторное произведение двух сторон треугольника

Добавляются нормали в той же последовательности, что и вершины.
В итоге у каждого треугольного сегмента есть
- Mesh Positions (положение точки на поверхности)
- Triangle Indeces (определяет одну из трех точек на треугольнике)
- Triangle Normals (нормали)
Начало системы координат при работе с 3D графикой находится в в центре сцены, в отличии от 2D, где начало в левом верхнем углу. Отображает графическое содержание сцены класс Viewport3D

Так как представление 3D объектов на экране это фактически двумерные проекции, то следует выбрать точку наблюдения, от которой и будет зависеть вид объекта. В WPF эту точку помогает указать класс camera
Тор
Тор — это поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности.

Уравнения тора можно представить в параметрическом и алгебраическом виде, в данном случае удобнее пользоваться
параметрическим.
x = (R + r * cos(a)) * cos(b)
y = r * sin (a)
z = -(R + r * cos(a))sin(b)
Тор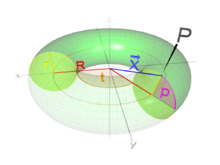

Закодируем уравнение тора.
Данный метод просто возвращает точку по заданным радиусам и углам:
public Point3D getPositionTor(double R, double r, double a, double v){
double sinB = Math.Sin(B * Math.PI / 180);
double cosB = Math.Cos(B * Math.PI / 180);
double sinA = Math.Sin(A * Math.PI / 180);
double cosA = Math.Cos(A * Math.PI / 180);
Point3D point = new Point3D();
point.X = (R + r * cosA) * cosB;
point.Y = r * sinA;
point.Z = -(R + r * cosA) * sinB;
return point;
}
Создадим метод построения треугольного сегмента
public static void drawTriangle(
Point3D p0, Point3D p1, Point3D p2, Color color, Viewport3D viewport) {
MeshGeometry3D mesh = new MeshGeometry3D();
mesh.Positions.Add(p0);
mesh.Positions.Add(p1);
mesh.Positions.Add(p2);
mesh.TriangleIndices.Add(0);
mesh.TriangleIndices.Add(1);
mesh.TriangleIndices.Add(2);
SolidColorBrush brush = new SolidColorBrush();
brush.Color = color;
Material material = new DiffuseMaterial(brush);
GeometryModel3D geometry = new GeometryModel3D(mesh, material);
ModelUIElement3D model = new ModelUIElement3D();
model.Model = geometry;
viewport.Children.Add(model);
}
Все готово для отрисовки тора.
Сегмент тора

Строим сегменты представленные на рисунке выше, каждый из которых является объединением двух треугольников построенных на четырех вершинах.
public void drawTor(Point3D center, double R, double r, int N, int n, Color color){
if (n < 2 || N < 2){
return;
}
Model3DGroup tor = new Model3DGroup();
Point3D[,] points = new Point3D[N, n];
for (int i = 0; i < N; i++){
for (int j = 0; j < n; j++){
points[i, j] = getPositionTor(R, r, i * 360/(N - 1), j * 360/(n - 1));
points[i, j] += (Vector3D)center;
}
}
Point3D[] p = new Point3D[4];
for (int i = 0; i < N - 1; i++){
for (int j = 0; j < n - 1; j++){
p[0] = points[i, j];
p[1] = points[i + 1, j];
p[2] = points[i + 1, j + 1];
p[3] = points[i, j + 1];
drawTriangle(p[0], p[1], p[2], color, mainViewport);
drawTriangle(p[2], p[3], p[0], color, mainViewport);
}
}
}
Остается вызвать метод отрисовки тора
drawTor(new Point3D(0, 0, 0), 1.0, 0.3, 20, 15, Colors.Tomato, false);
Графический интерфейс делается с XAML очень быстро, приведу лишь добавление ViewPort3D
<Viewport3D Name="mainViewport" ClipToBounds="True" Height="374">
<Viewport3D.Camera>
<PerspectiveCamera
FarPlaneDistance="100"
LookDirection="-11,-10,-9"
UpDirection="0,1,0"
NearPlaneDistance="1"
Position="11,10,9"
FieldOfView="70"/>
</Viewport3D.Camera>
<ModelVisual3D>
<ModelVisual3D.Content>
<DirectionalLight
Color="White"
Direction="-2,-3,-1"/>
</ModelVisual3D.Content>
</ModelVisual3D>
</Viewport3D>
Вот, что получилось в итоге:

И удалим несколько сегментов

Спасибо за внимание.
