Проглядывая книжку «Эффективное использование C++», Скотта Мейерса, которая ( и я никого не удивлю ) достойна всяческих похвал, меня очень тронуло, то с какой возбуждённостью, вдохновлённостью, трепетом ( может мне показалось? ) автор говорит о шаблонах и их возможностях. Приведу маленький кусочек:
Да уж… сердце забилось, в очередной раз удивился — только подумать — полная машина Тьюринга со всеми вытекающими последствиями… Как по мне, это просто невероятно и удивительно… хотя, кто его знает…
Предлагаю посмотреть на совсем уж маленький кусочек мира больших возможностей и невероятных приключений — попробуем вычислить на этапе компиляции значение, небезызвестного, числа e.
Как её вычислять (с некоторой погрешностью) — подскажет ряд Тейлора, а точнее ряд Маклорена:
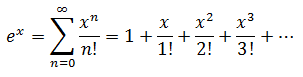
Т.е. нам нужно будет уметь считать факториал числа, возводить в степень, суммировать и работать с дробными числами… и всё это с помощью шаблонов C++.
Для начала хотелось бы разобраться с дробными числами — нужно как-то сохранять числитель и знаменатель, и иметь также доступ к ним ( N — Numerator, D — Denominator ):
Всё просто, но как насчёт нулевого знаменателя? Попробуем это:
Используем:
В случае с msvc10 мы получим что-то вроде
Итак, сохранять 2 числа умеем, а как же насчёт сокращения дробей? Тут надо уже научиться находить gcd (Наиболее общий делитель) двух чисел — нам подходит рекурсивный алгоритм:
который превращается с помощь шаблонов в:
Всё просто, не так ли? — пишем наиболее общую реализацию шаблона и делаем частную специализацию для частных случаев (если второе число ноль — результат — это первое число).
С помощью всего выше написанного, делаем окончательную версию дробного числа:
С помощью известных формул — делим, множим, отнимаем, добавляем наши числа:
Снова же — пишем пустой набросок нашей "функции", например
Также нам нужно возведение в степень и факториал, определение которых говорит само о себе:
Итак, теперь у нас есть весь набор всего необходимого, чтобы реализовать формулу выше — понятно суммировать мы будем не до бесконечности, а сколько сможем, т.е. например, выражение
Проблема возникает в том, а как нам суммировать дробные числа, которые даже не являются числовыми значениями — это всего лишь типы! Да, они содержат в себе числовые данные, но к ним еще нужно добраться в ходе подсчёта суммы ряда… Но решение есть и оно состоит в том, что мы можем достать из производного класса данные (и typedef-ы — самое важное) базового класса. Именно! — чтобы подсчитать сумму ряда, нам нужно будет наследоваться и наследоваться, и наследоваться… в идеале до бесконечности.
Кусок кода:
И что в итоге, а в итоге мы с гордостью можем написать следущее:
на 32 битной машине больше 8ми членов ряда взять не получится — переполнение
Результат: 2.718279 (109601/40320).
Волшебство :)
Надеюсь, Вам было приятно. Спасибо за внимание.
PS: отдельно извиняюсь за орфографические, синтаксические ошибки — был в сонном несостоянии, недоумении и восторге.
Метапрограммирование шаблонов ( template metaprogramming — TMP ) — это процесс написания основанных на шаблонах программ на C++, исполняемых во время компиляции. На минуту задумайтесь об этом: шаблонная метапрограмма — это программа, написанная на C++, которая исполняется внутри компилятора C++…
Было доказано, что технология TMP предоставляет собой полную машину Тьюринга, то есть обладает достаточной мощь для любых вычислений...
Да уж… сердце забилось, в очередной раз удивился — только подумать — полная машина Тьюринга со всеми вытекающими последствиями… Как по мне, это просто невероятно и удивительно… хотя, кто его знает…
Предлагаю посмотреть на совсем уж маленький кусочек мира больших возможностей и невероятных приключений — попробуем вычислить на этапе компиляции значение, небезызвестного, числа e.
Как её вычислять (с некоторой погрешностью) — подскажет ряд Тейлора, а точнее ряд Маклорена:
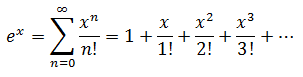
Т.е. нам нужно будет уметь считать факториал числа, возводить в степень, суммировать и работать с дробными числами… и всё это с помощью шаблонов C++.
Для начала хотелось бы разобраться с дробными числами — нужно как-то сохранять числитель и знаменатель, и иметь также доступ к ним ( N — Numerator, D — Denominator ):
template<int n, int d> struct Fractional { enum { N = n, D = d }; };
Всё просто, но как насчёт нулевого знаменателя? Попробуем это:
template<int n, int d> struct Fractional { private: enum { NonZeroDenominator = n / d }; public: enum { N = n, D = d }; };
Используем:
typedef Fractional<9, 0> number; // ... int temp = number::D;
В случае с msvc10 мы получим что-то вроде
error C2057: expected constant expression — невнятно, но если пойти к месту ошибки — то как раз увидим переменную NonZeroDenominator — уже хоть что-то…Итак, сохранять 2 числа умеем, а как же насчёт сокращения дробей? Тут надо уже научиться находить gcd (Наиболее общий делитель) двух чисел — нам подходит рекурсивный алгоритм:
int gcd(int a, int b) { if(b == 0) return a; return gcd(b, a % b); }
который превращается с помощь шаблонов в:
template<int n1, int n2> struct GCD { enum { value = GCD<n2, n1 % n2>::value }; }; template<int n1> struct GCD<n1, 0> { enum { value = n1 }; };
Всё просто, не так ли? — пишем наиболее общую реализацию шаблона и делаем частную специализацию для частных случаев (если второе число ноль — результат — это первое число).
С помощью всего выше написанного, делаем окончательную версию дробного числа:
template<int n, int d> struct Fractional { private: enum { NonZeroDenominator = n / d }; enum { gcd = GCD<n, d>::value }; public: enum { N = n / gcd, D = d / gcd }; };
С помощью известных формул — делим, множим, отнимаем, добавляем наши числа:
// // Divide // template<typename n, typename d> struct Divide { }; template<int n1, int d1, int n2, int d2> struct Divide<Fractional<n1, d1>, Fractional<n2, d2> > { private: typedef Fractional<n1, d1> n; typedef Fractional<n2, d2> d; public: typedef Fractional<n::N * d::D, n::D * d::N> value; }; // // Multiple // template<typename n, typename d> struct Multiple { }; template<int n1, int d1, int n2, int d2> struct Multiple<Fractional<n1, d1>, Fractional<n2, d2> > { private: typedef Fractional<n1, d1> n; typedef Fractional<n2, d2> d; public: typedef Fractional<n::N * d::N, n::D * d::D> value; }; // // Substract // template<typename n, typename d> struct Substract { }; template<int n1, int d1, int n2, int d2> struct Substract<Fractional<n1, d1>, Fractional<n2, d2> > { private: typedef Fractional<n1, d1> n; typedef Fractional<n2, d2> d; public: typedef Fractional<n::N * d::D - d::N * n::D, n::D * d::D> value; }; // // Add // template<typename n, typename d> struct Add { }; template<int n1, int d1, int n2, int d2> struct Add<Fractional<n1, d1>, Fractional<n2, d2> > { private: typedef Fractional<n1, d1> n; typedef Fractional<n2, d2> d; public: typedef Fractional<n::N * d::D + d::N * n::D, n::D * d::D> value; };
Снова же — пишем пустой набросок нашей "функции", например
Divide — отмечая, что она (функция) принимает 2 аргумента. И дальше с помощью частичной специализации шаблона уточняем, что хотим видеть не что нибудь, а именно идентификатор шаблона нужного нам, т.е. Divide<n1, n2>, к примеру. Использование:typedef Fractional<4, 20> n1; typedef Fractional<5, 32> n2; typedef Add<n1, n2>::value summ; printf("%i/%i\n", summ::N, summ::D); // 57/160
Также нам нужно возведение в степень и факториал, определение которых говорит само о себе:
// // Factorial // template<int N> struct Factorial { enum { value = N * Factorial<N - 1>::value }; }; template<> struct Factorial<0> { enum { value = 1 }; }; // // Power // template<int x, int n> struct Pow { enum { value = x * Pow<x, n - 1>::value }; }; template<int x> struct Pow<x, 0> { enum { value = 1 }; };
Итак, теперь у нас есть весь набор всего необходимого, чтобы реализовать формулу выше — понятно суммировать мы будем не до бесконечности, а сколько сможем, т.е. например, выражение
Exp<4, 8>::value будет давать дробное число, которое численно равно экспоненте в 4й степени и суммирование произведено всего лишь до 8 (бесконечность рядом) члена включительно.Проблема возникает в том, а как нам суммировать дробные числа, которые даже не являются числовыми значениями — это всего лишь типы! Да, они содержат в себе числовые данные, но к ним еще нужно добраться в ходе подсчёта суммы ряда… Но решение есть и оно состоит в том, что мы можем достать из производного класса данные (и typedef-ы — самое важное) базового класса. Именно! — чтобы подсчитать сумму ряда, нам нужно будет наследоваться и наследоваться, и наследоваться… в идеале до бесконечности.
Кусок кода:
// // Exponent // template<int x, int n> struct Exp : public Exp<x, n - 1> { private: typedef typename Exp<x, n - 1>::value previous; protected: typedef Fractional<Pow<x, n>::value, Factorial<n>::value> current; public: typedef typename Add<current, previous>::value value; }; template<int x> struct Exp<x, 0> { public: typedef Fractional<Pow<x, 0>::value, Factorial<0>::value> current; public: typedef current value; };
current содержит в себе значение одного члена ряда — т.е. один класс в этой целой иерархии классов, грубо говоря, предназначен для хранения значения одного члена. А с помощью того, что он может взять данные базового класса — т.е. значение предыдущего члена ряда — то всё это даёт нам то, что кроме значения одного отдельного элемента ряда, мы в текущем классе имеем сумму ряда до этого элемента (класса) включительно.И что в итоге, а в итоге мы с гордостью можем написать следущее:
int main() { // дробь typedef Exp<1, 8>::value result; printf("%i/%i\n", result::N, result::D); // десятичное представление printf("%f\n", result::N / static_cast<float>(result::D)); }
на 32 битной машине больше 8ми членов ряда взять не получится — переполнение
int.Результат: 2.718279 (109601/40320).
Волшебство :)
Надеюсь, Вам было приятно. Спасибо за внимание.
PS: отдельно извиняюсь за орфографические, синтаксические ошибки — был в сонном несостоянии, недоумении и восторге.
