1. Основы
Большинство из нас, хабражителей, знает, что такое судоку. Не буду рассказывать про правила, а сразу перейду к методикам.
Для решения головоломки, не важно сложной или простой, изначально ищутся ячейки очевидные для заполнения.
1.1 «Последний герой»
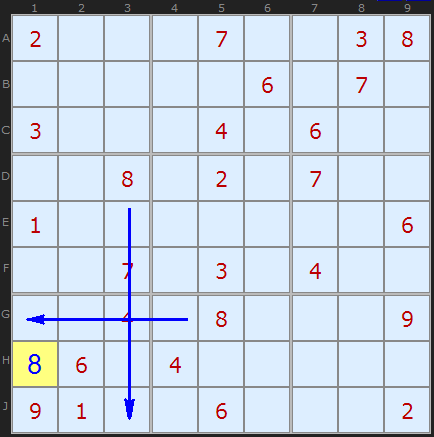
Рассмотрим седьмой квадрат. Всего четыре свободных клетки, значит что-то можно быстро заполнить.
"8" на D3 блокирует заполнение H3 и J3; точно также "8" на G5 закрывает G1 и G2
С чистой совестью ставим "8" на H1
1.2 «Последний герой» в строке
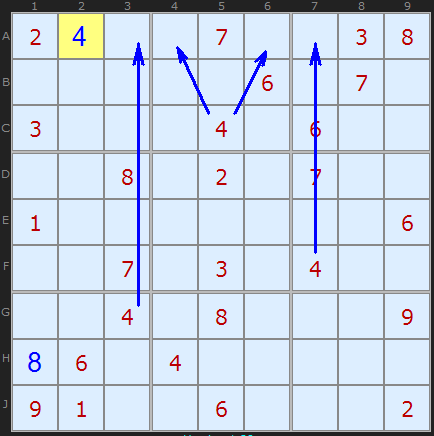
После просмотра квадратов на очевидные решения, переходим к столбцам и строкам.
Рассмотрим "4" на поле. Понятно, что она будет где-то в строке A.
У нас есть "4" на G3, что зыкрывает A3, есть "4" на F7, убирающая A7. И ещё одна "4" во втором квадрате запрещает её повтор на A4 и A6.
«Последний герой» для нашей "4" это A2
1.3 «Выбора нет»
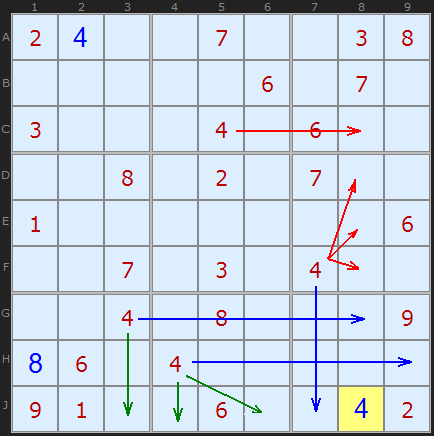
Иногда есть несколько причин для конкретного расположения. "4" в J8 будет отличным примером.
Синие стрелки показывают, что это последнее возможное число в квадрате. Красные и синие стрелки дают нам последнее число в столбце 8. Зеленые стрелки дают последнее возможное число в строке J.
Как видим, выбора у нас нет, кроме как поставить эту "4" на место.
1.4 «А кто, как не я?»
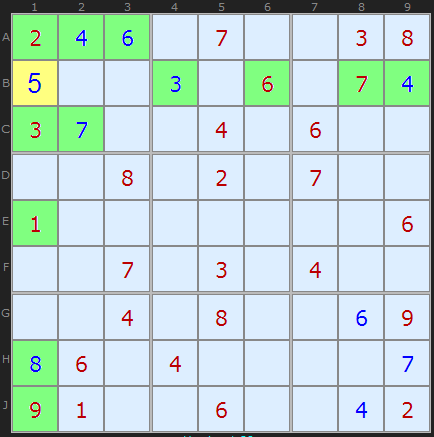
Заполнение чисел проще проводить вышеописанными методами. Однако проверка числа, как последнего возможного значения, тоже даёт результаты. Метод стоит применять, когда кажется, что все числа есть, но чего-то не хватает.
"5" в B1 ставится исходя из того, что все числа от "1" до "9", кроме "5" есть в строке, столбце и квадрате (отмечено зеленым).
На жаргоне это "Голая одиночка". Если заполнять поле возможными значениями (кандидатами), то в ячейке такое число будет единственным возможным. Развивая эту методику, можно искать "Скрытые одиночки" — числа, уникальные для конкретной строки, столбца или квадрата.
2. «Голая миля»
2.1 «Голые» пары
"«Голая» пара" — набор из двух кандидатов, расположенных в двух ячейках, принадлежащих одному общему блоку: строке, столбцу, квадрату.
Понятно, что правильные решения головоломки будут только в этих ячейках и только с этими значениями, в то время как все другие кандидаты из общего блока могут быть убраны.
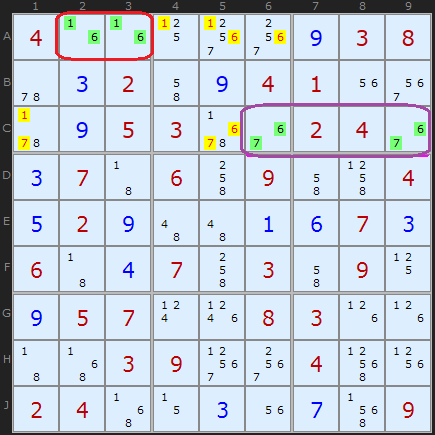
В этом примере несколько «голых пар».
Красным в строке А выделены ячейки А2 и А3, обе содержащие "1" и "6". Я пока не знаю, как именно они расположены здесь, но я спокойно могу убрать все другие "1" и "6" из строки A (отмечено желтым). Также А2 и А3 принадлежат общему квадрату, поэтому убираем "1" из C1.
2.2 «Threesome»
«Голые тройки» — усложненный вариант «голых пар».
Любая группа из трех ячеек в одном блоке содержащая в общем три кандидата является «голой тройкой». Когда такая группа нашлась, эти три кандидата могут быть убраны из других ячеек блока.
Комбинации кандидатов для «голой тройки» могуть быть такими:
[abc] [abc] [abc] // три числа в трех ячейках.
[abc] [abc] [ab] // любые комбинации.
[abc] [ab] [ab] // любые комбинации.
[ab] [aс] [bc]
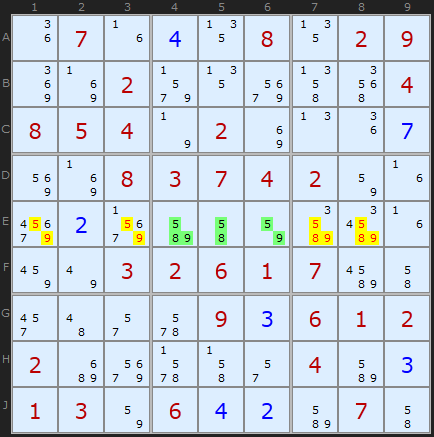
В этом примере все довольно очевидно. В пятом квадрате ячейки E4, E5, E6 содержат [5,8,9], [5,8], [5,9] соответственно. Получается, что в общем у этих трех ячеек есть [5,8,9], и только эти числа там могут быть. Это позволяет нам убрать их из других кандидатов блока. Этот трюк даёт нам решение "3" для ячейки E7.
2.3 «Великолепная четверка»
"«Голая» четверка" весьма редкое явление, особенно в полной форме, и все же дает результаты при обнаружении. Логика решения такая же как и у «голых троек».
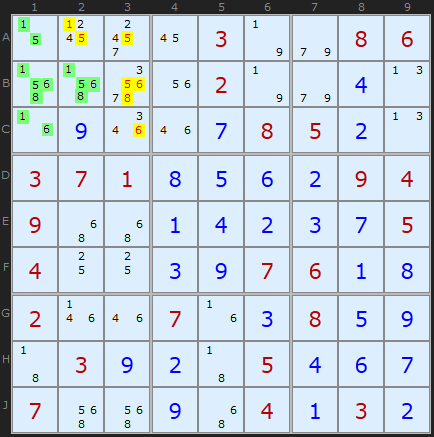
В указанном примере в первом квадрате ячейки A1, B1, B2 и C1 в общем содержат [1,5,6,8], поэтому эти числа займут только эти ячейки и никакие другие. Убираем подсвеченных желтым кандидатов.
3. «Все тайное становится явным»
3.1 Скрытые пары
Отличным способом раскрыть поле будет поиск скрытых пар. Этот метод позволяет убрать лишних кандидатов из ячейки и дать развитие более интересным стратегиям.
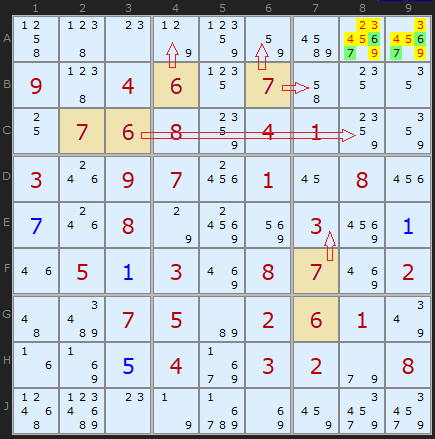
В этой головоломке мы видим, что 6 и 7 есть в первом и втором квадратах. Кроме этого 6 и 7 есть в столбце 7. Комбинируя эти условия, мы можем утверждать, что в ячейках A8 и A9 будут только эти значения и все другие кандидаты мы убираем.
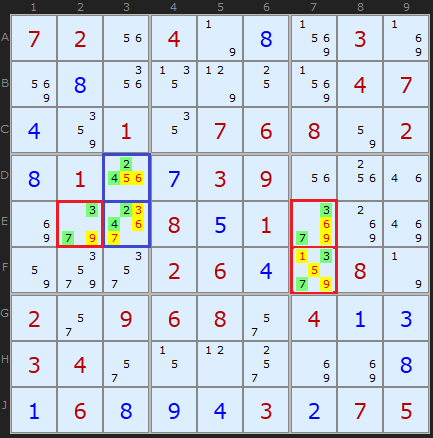
Более интересный и сложный пример скрытых пар. Синим выделена пара [2,4] в D3 и E3, убирающая 3, 5, 6, 7 из этих ячеек. Красным выделены две скрытые пары, состоящие из [3,7]. C одной стороны, они уникальны для для двух ячеек в 7 столбце, с другой стороны — для строки E. Выделеные желтым кандидаты убираются.
3.1 Скрытые тройки
Мы можем развить скрытые пары до скрытых троек или даже скрытых четверок. Скрытая тройка состоит из трех пар чисел, расположенных в одном блоке. Такие как [a,b,c], [a,b,c] и[a,b,c]. Однако, как и в случае с «голыми тройками», в каждой из трех ячеек не обязательно должно быть по три числа. Сработают всего три числа в трех ячейках. Например [ab], [aс], [bc]. Скрытые тройки будут замаскированы другими кандидатами в ячейках, поэтому сначала надо убедиться, что тройка применима к конкретному блоку.
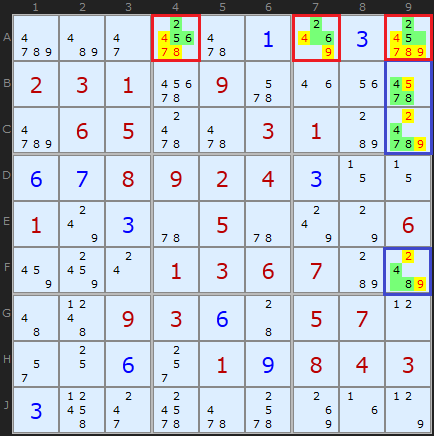
В этом сложном примере есть две скрытые тройки. Первая, отмеченная красным, в столбце А. Ячейка А4 содержит [2,5,6], A7 — [2,6] и ячейка A9 -[2,5]. Эти три ячейки единственные, где могут быть 2 ,5 или 6, поэтому только они там и будут. Следовательно убираем лишних кандидатов.
Вторая, в столбце 9. [4,7,8] уникальны для ячеек B9, C9 и F9. Используя ту же логику, убираем кандидатов.
3.1 Скрытые четверки
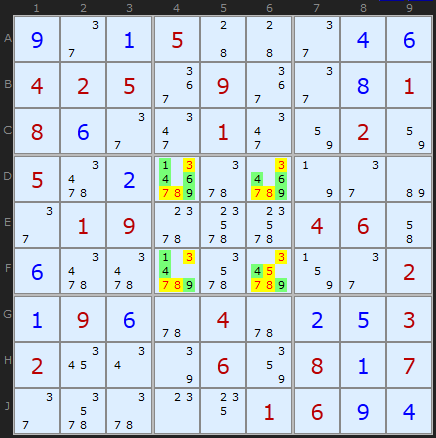
Прекрасный пример скрытых четверок. [1,4,6,9] в пятом квадрате могут быть только в четырех ячейках D4, D6, F4, F6. Следуя нашей логике, убираем всеъ других кандидатов (отмеченых желтым).
4. «Нерезиновая»
Если любое из чисел появляется дважды или трижды в одном блоке (строке, столбце, квадрате), тогда мы можем убрать это число из сопряженного блока. Есть четыре вида сопряжения:
- Пара или Тройка в квадрате — если они расположены в одной строке, то можно убрать все другие такие же значения из соответствующей строки.
- Пара или Тройка в квадрате — если они расположены в одном столбце, то можно убрать все другие такие же значения из соответствующего столбца.
- Пара или Тройка в строке — если они расположены в одном квадрате, то можно убрать все другие такие же значения из соответствующего квадрата.
- Пара или Тройка в столбце — если они расположены в одном квадрате, то можно убрать все другие такие же значения из соответствующего квадрата.
4.1 Указавыющие пары, тройки
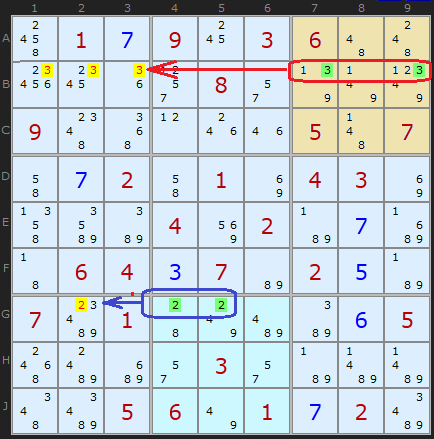
В качестве примера покажу эту головоломку. В третьем квадрате "3" находится только в B7 и B9. Следуя утверждению №1, мы убираем кандидатов из B1, B2, B3. Аналогично, "2" из восьмого квадрата убирает возможное значение из G2.
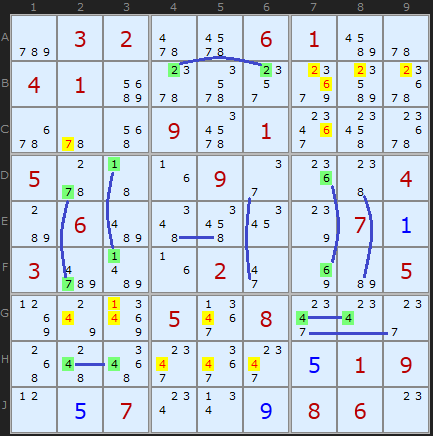
Особенная головоломка. Очень сложная в решении, но, если присмотреться, можно заметить несколько указывающих пар. Понятно, что не всегда обязательно находить их все, чтобы продвинуться в решении, однако каждая такая находка облегчает нам задачу.
4.2 Сокращаем несокращаемое
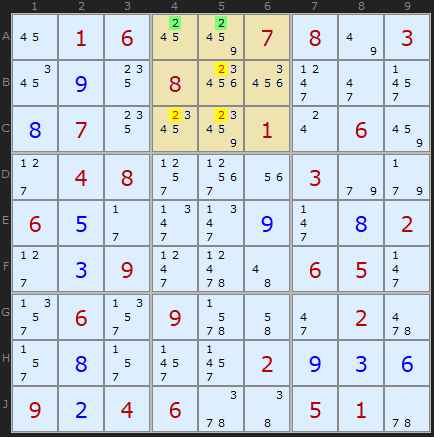
Эта стратегия включает в себя аккуратный анализ и сравнение строк и столбцов с содержимым квадратов (правила №3, №4).
Рассмотрим строку А. "2" возможны только в А4 и А5. Следуя правилу №3, убираем "2" их B5, C4, C5.
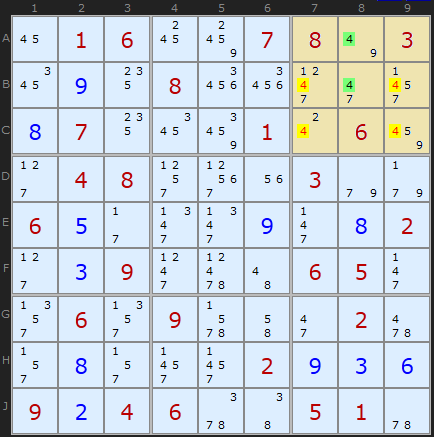
Продолжим решать головоломку. Имеем единственное расположение "4" в пределах одного квадрата в 8 столбце. Согласно правилу №4, убираем лишних кандитатов и, в добавок, получаем решение "2" для C7.
Послесловие
Существуют сотни алгоритмов и программ для решения судоку. Иногда для получения результата достаточно навести вебкамеру. Однако для тренировки мозга и прокручивания алгоритмов в голове будет полезно посидеть с ручкой и бумагой, решая судоку.
В статье привел базовые алгоритмы решения. Да-да, именно базовые. Следующим шагом будет разбор продвинутых и сложных методик. Спасибо за внимание.
