Здравствуй, Хабрахабр!
Не так давно где-то на просторах одной социальной сети увидел следующую игру: игроки присылают ведущему (назовем его так) по целому положительному числу (игроки не знают чисел друг друга), побеждает тот, кто прислал наименьшее уникальное число. Например, если играют 7 игроков и они прислали числа 5, 4, 2, 1, 1, 2, 6, побеждает игрок приславший число 4. Стало мне жутко интересно, как же надо «правильно» играть в эту игру, но оказалось, что однозначное решения для n игроков здесь если и есть, то оно достаточно сложное и запутанное, поэтому рассмотрим конкретные случаи для 3-х и 4-х игроков.
Итак, поехали. Для начала, введем ограничение: пусть игроки могут выбирать числа только из {1, 2, 3} (потом будет проще и очевиднее переход к выбору любого натурального числа). Что мы попытаемся сейчас сделать: найти такую смешанную стратегию
, что когда бы все игроки придерживались данной стратегии, никто бы не мог увеличить шансы на победу, изменив свою стратегию (такая штука, кстати, называется, равновесием Нэша). То есть, чтобы каждый игрок с вероятностью 
выбирал число 1, с вероятностью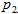 
– число 2 и с вероятностью 
– 3, и каждому из игроков было бы невыгодно отклоняться от этих вероятностей.
Допустим, что игроки 2 и 3 используют эти вероятности, а игрок 1 решил увеличить свои шансы на победу и теперь использует стратегию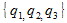
. Чтобы победить, он должен выбрать число 1 (а остальные игроки должны выбрать или оба 2, или оба 3, или один 2, а второй – 3), число 2 (остальные же должны выбрать или оба 1, или оба 3), или же 3 (в таком случае остальные должны или оба выбирать 1, или оба выбирать 2). Таким образом, итоговая вероятность победы 
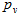может быть выражена как сумма этих трёх вероятностей: 
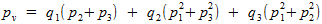(1). Не забываем также и о том, что сумма всех вероятностей в конечном итоге равна единице, т. е. 
(*).
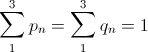Итак, игроку 1 нужно попытаться увеличить свою вероятность на победу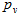, но у нас есть ограничение (*). На выручку приходит славный метод множителей Лагранжа, который делает как раз то, что нам нужно — находит локальные экстремумы функции (у нас это функция (1)) при имеющихся ограничениях на некоторые равенства (у нас – равенство (*)). Уравнение Лагранжа 
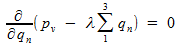даёт нам следующие уравнения:
,
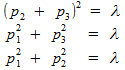которые мы и решаем, принимая во внимание, конечно же, равенство (*). Получаем следующие вероятности:
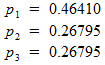
Готово! Какой из этого вывод? Когда 3 игрока могут выбирать только из {1, 2, 3}, для каждого из них оптимальной стратегией будет следующая: приблизительно в половине случаев выбирать 1, приблизительно в четверти – выбирать 2, и приблизительно в четверти – 3. Это и будет равновесием Нэша.
Итак, что же произойдет, если мы снимем ограничения на множество, из которого игроки могут выбирать числа и как нам найти равновесие Нэша для такой игры? Теперь, если игрок выбирает некоторое число i, победит он только в том случае, если все игроки выберут одно и то же число строго меньше i, или же оба выберут по числу, каждое из которых строго больше i. Таким образом, для каждого игрока вероятность победы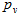 следующая: 
. Дифференцируя данное уравнение, получаем бесконечное множество уравнений: 
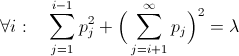и ограничение 
. Такая штуковина решаема, но достаточно сложно, поэтому просто приведу здесь ответ:
.
Что всё это значит? Если подставить в полученное уравнение конкретные числа, то для первой семерки получаем приблизительно следующие вероятности:
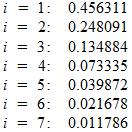
То есть, равновесием Нэша будет такой набор стратегий, где каждый игрок с вероятностью приблизительно 0.46 выбирает 1, с вероятностью 0.25 – 2, с вероятностью 0.13 – 3, и так далее.
Та же игра, с четырьмя игроками не сильно отличается от игры с тремя. В этом случае функция, которую нужно максимизировать, имеет следующий вид:
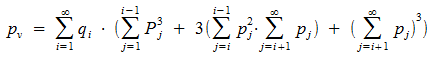
Что здесь к чему:
Решение имеет следующий вид:
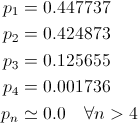
Отсюда следует, что чаще всего придется выбирать числа 1 и 2, изредка — 3, очень изредка – 4, и с числами больше четырёх дело иметь почти не приходится.
Спасибо за внимание. Играйте в игры.
Не так давно где-то на просторах одной социальной сети увидел следующую игру: игроки присылают ведущему (назовем его так) по целому положительному числу (игроки не знают чисел друг друга), побеждает тот, кто прислал наименьшее уникальное число. Например, если играют 7 игроков и они прислали числа 5, 4, 2, 1, 1, 2, 6, побеждает игрок приславший число 4. Стало мне жутко интересно, как же надо «правильно» играть в эту игру, но оказалось, что однозначное решения для n игроков здесь если и есть, то оно достаточно сложное и запутанное, поэтому рассмотрим конкретные случаи для 3-х и 4-х игроков.
Случай трёх игроков
Выбор из {1, 2, 3}
Итак, поехали. Для начала, введем ограничение: пусть игроки могут выбирать числа только из {1, 2, 3} (потом будет проще и очевиднее переход к выбору любого натурального числа). Что мы попытаемся сейчас сделать: найти такую смешанную стратегию
, что когда бы все игроки придерживались данной стратегии, никто бы не мог увеличить шансы на победу, изменив свою стратегию (такая штука, кстати, называется, равновесием Нэша). То есть, чтобы каждый игрок с вероятностью 
выбирал число 1, с вероятностью 
– число 2 и с вероятностью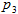 
– 3, и каждому из игроков было бы невыгодно отклоняться от этих вероятностей.Допустим, что игроки 2 и 3 используют эти вероятности, а игрок 1 решил увеличить свои шансы на победу и теперь использует стратегию
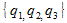. Чтобы победить, он должен выбрать число 1 (а остальные игроки должны выбрать или оба 2, или оба 3, или один 2, а второй – 3), число 2 (остальные же должны выбрать или оба 1, или оба 3), или же 3 (в таком случае остальные должны или оба выбирать 1, или оба выбирать 2). Таким образом, итоговая вероятность победы 
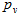может быть выражена как сумма этих трёх вероятностей: 
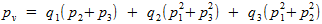(1). Не забываем также и о том, что сумма всех вероятностей в конечном итоге равна единице, т. е. 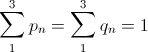(*). Итак, игроку 1 нужно попытаться увеличить свою вероятность на победу
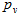, но у нас есть ограничение (*). На выручку приходит славный метод множителей Лагранжа, который делает как раз то, что нам нужно — находит локальные экстремумы функции (у нас это функция (1)) при имеющихся ограничениях на некоторые равенства (у нас – равенство (*)). Уравнение Лагранжа 
даёт нам следующие уравнения: 
,которые мы и решаем, принимая во внимание, конечно же, равенство (*). Получаем следующие вероятности:
Готово! Какой из этого вывод? Когда 3 игрока могут выбирать только из {1, 2, 3}, для каждого из них оптимальной стратегией будет следующая: приблизительно в половине случаев выбирать 1, приблизительно в четверти – выбирать 2, и приблизительно в четверти – 3. Это и будет равновесием Нэша.
Выбор любого натурального числа
Итак, что же произойдет, если мы снимем ограничения на множество, из которого игроки могут выбирать числа и как нам найти равновесие Нэша для такой игры? Теперь, если игрок выбирает некоторое число i, победит он только в том случае, если все игроки выберут одно и то же число строго меньше i, или же оба выберут по числу, каждое из которых строго больше i. Таким образом, для каждого игрока вероятность победы
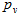следующая: 
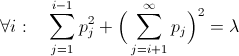. Дифференцируя данное уравнение, получаем бесконечное множество уравнений: и ограничение 
. Такая штуковина решаема, но достаточно сложно, поэтому просто приведу здесь ответ: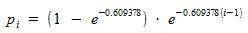 
.Что всё это значит? Если подставить в полученное уравнение конкретные числа, то для первой семерки получаем приблизительно следующие вероятности:
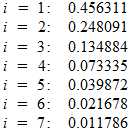
То есть, равновесием Нэша будет такой набор стратегий, где каждый игрок с вероятностью приблизительно 0.46 выбирает 1, с вероятностью 0.25 – 2, с вероятностью 0.13 – 3, и так далее.
Случай четырёх игроков
Та же игра, с четырьмя игроками не сильно отличается от игры с тремя. В этом случае функция, которую нужно максимизировать, имеет следующий вид:
Что здесь к чему:
Решение имеет следующий вид:
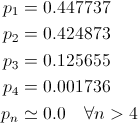
Отсюда следует, что чаще всего придется выбирать числа 1 и 2, изредка — 3, очень изредка – 4, и с числами больше четырёх дело иметь почти не приходится.
Спасибо за внимание. Играйте в игры.
