Легкий и «полупраздничный» пост. Всех причастных с праздником :)
Одной из самых захватывающих вещей в восьмидесятые было программное моделирование для решения каких-нибудь сложных аналитических проблем и одной из самых используемых техник был метод Монте-Карло. Заключается он в том, что запускает моделирование большое количество раз для получения все более и более достоверного результата.
Несмотря на то, что PHP не является научным языком и редко используется в исследовательских целях, метод Монте-Карло легко может быть реализован и на нём. И в данной статье я покажу как это сделать.
Пару дней назад у меня должна быть встреча в 9 часов утра, за 100 миль от моего дома. В 6.30 утра я проснулся, оделся и пока я завтракал, я начал прикидывать в блокноте ближайшие пару часов. Я, как обычно, хотел приехать вовремя, поэтому я начал набрасывать маршрут: выезд из города, проселочная дорога, затем по штату на север, на восток, местная дорога на восток, проехать город, затем на снова на север и прибытие в город. Все это выглядело как-то так:
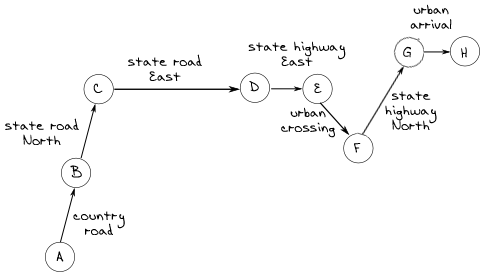
Моя жена заполнила бак прошлым вечером и я спокойно мог ехать по проселочной дороге. Шины, казалось, были в порядке, когда я смотрел на них, но мысль о том, делать или нет остановку на 10 минут, чтобы проверить их давление, не давала мне покоя. Ведь если я остановлюсь и проверю их, то я буду уверен в их давлении, так как сейчас в нем не был уверен, да и давление в шинах может повлиять на мое движение и скорость…
Я могу выезжать раньше, например, в 6.40, но тогда моей жене придется самой отводить дочь в школу, вместо того чтобы прямиком идти на работу. Если я подожду еще 10 минут, то я могу быть у школы как раз в тот момент, когда они только открывают свои двери, тем самым избавив мою жену от неудобств, тем более что школа по пути к выезду из города и это не сильно меня задерживало.
Я вернулся к тому, что я рисовал и добавил следующее:
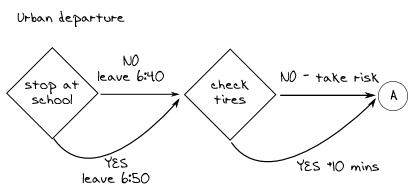
Выпивая вторую чашку кофе, я встал у окна. Чистое утреннее небо, легкий утренний ветерок подтверждали хороший прогноз на моем смартфоне и я подумал, что поездка в этот раз будет быстрой. Заканчивая свое планирование, я нарисовал примерное время для каждого этапа, которые я нарисовал ранее:
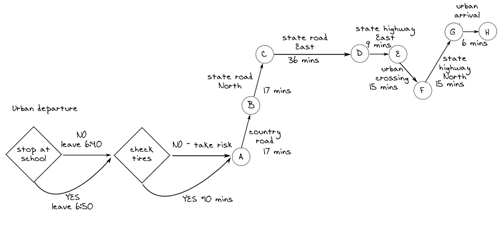
Ожидаемое время поездки было 115 минут (1 час и 55 минут), если я смогу двигаться без лишних остановок. Я ожидал приехать в 8.35, если поеду сразу, или же в 8.55, если придется захватить с собой дочь, чтобы отправить ее в школу и заодно проверить шины.
Но любое планирование перестает быть идеальным после того, как столкнется с реальностью! По каким-то непонятным причинам, многие родители решают оставить своих детей в школе раньше, чем обычно, поэтому я потерял больше 5 минут, по сравнению с тем, что я планировал для своей быстрой поездки. Поняв, что я немного опаздываю, я решил не проверять давление в шинах и ехать сразу.
Я добрался до выезда из города на 5 минут раньше, чем я планировал в самом плохом раскладе дел и все шло хорошо ровно до тех пор, пока где-то между точками B и C в моем плане я не наткнулся на туман, сильно повлиявший на видимость на дороге. Туман снизил мою среднюю скорость? да еще и мешал обгонять медленные, но длинные грузовики. Городской поток в городе я преодолел намного легче, чем обычно и это не заняло больше 10 минут. Через несколько миль на южной дороге туман снизился и я мог спокойно ехать на разрешенной скорости. Но когда я приближался к моей цели, я понял, что впереди идут дорожные работы и это опять отнимет у меня запланированное время. В общем и целом я потратил еще 10 лишних минут на мое путешествие и в конце-концов я опоздал.
Я понимаю, что большая часть работы с PHP направлена на всякие там интернет-магазины и другие вебсайты. Но PHP может быть прекрасным инструментом для научных исследований, поскольку ему легко обучить непрофессиональных программистов, таких как инженеры и ученые, в отличии от моего любимого Python.
Напишем небольшой код, который поможет мне понять насколько раньше или позже я смогу прибыть на встречу, если пара этапов моего путешествия немного отойдут от намеченного пути. Для начала, можно описать наш путь как он есть:
План должен быть осуществимым и подходящим критерием для определения этого будет таким, что сумма всех времен плюс раннее время выезда должна быть меньше или равна времени, на которое назначена моя встреча. Собственно это и определяет метод checkPlan():
Все, нам осталось только сделать экземпляр этого класса и проверить:
С учетом настроек по умолчанию, вывод будет таким:
Я должен прибыть в 535 минут, а встреча назначена на 540 минут. Если перевести на часы, то я прибуду в 8.45, раньше запланированного времени на 15 минут.
Но что на счет возможных задержек? Как их предусмотреть и просчитать?
В самом простом виде мы можем определить некий безопасный зазор для каждого события и сказать что он может случиться на 10% раньше и на 25% позднее заданного времени. Эти зазоры могут быть случайно добавлены к изначальным задержкам (дочь, давление) и времени между этапами умножением каждого фактора на rand(90,125)/100.
Также можно присвоить 50% вероятность к двум решениям — отвезти дочь в школу и проверить шины. Тут снова поможет rand():
Объединив все это вместе можно определить метод checkPlanRisk() для вычисления решения приеду ли я вовремя или нет, с учетом разных ситуация во время пути:
Сейчас встает вопрос прибуду ли я вовремя, принимая во внимание все возможные задержи? Метод Монте-Карло позволяет решить этот вопрос запуском большого количества раз данной задачи и вычисляя «уровень доверия» как отношение времени прибытия вовремя к общему количеству запусков задачи.
Если запустить данный достаточное количество раз и записать как часто я прибуду вовремя, то я смогу определить некоторую вероятность того, что я прибуду как планировал.
Создадим новый экземпляр и сделаем 1000 вычислений друг за другом:
После завершения получим прогноз:
При текущих параметрах, как видно, у меня есть шанс в 72% прибыть на встречу вовремя. Конечно, это просто среднее значение, но и оно имеет право на жизнь.
От себя: скорее всего статья не несет абсолютно ничего нового, заголовок немного желтоват, но мне эта статья показалась забавной. Прочитал давно, а вспомнил с появлением статьи на хабре про Монте-Карло. Может кому-нибудь и пригодится.
Одной из самых захватывающих вещей в восьмидесятые было программное моделирование для решения каких-нибудь сложных аналитических проблем и одной из самых используемых техник был метод Монте-Карло. Заключается он в том, что запускает моделирование большое количество раз для получения все более и более достоверного результата.
Несмотря на то, что PHP не является научным языком и редко используется в исследовательских целях, метод Монте-Карло легко может быть реализован и на нём. И в данной статье я покажу как это сделать.
Задача из реальной жизни
Пару дней назад у меня должна быть встреча в 9 часов утра, за 100 миль от моего дома. В 6.30 утра я проснулся, оделся и пока я завтракал, я начал прикидывать в блокноте ближайшие пару часов. Я, как обычно, хотел приехать вовремя, поэтому я начал набрасывать маршрут: выезд из города, проселочная дорога, затем по штату на север, на восток, местная дорога на восток, проехать город, затем на снова на север и прибытие в город. Все это выглядело как-то так:

Моя жена заполнила бак прошлым вечером и я спокойно мог ехать по проселочной дороге. Шины, казалось, были в порядке, когда я смотрел на них, но мысль о том, делать или нет остановку на 10 минут, чтобы проверить их давление, не давала мне покоя. Ведь если я остановлюсь и проверю их, то я буду уверен в их давлении, так как сейчас в нем не был уверен, да и давление в шинах может повлиять на мое движение и скорость…
Я могу выезжать раньше, например, в 6.40, но тогда моей жене придется самой отводить дочь в школу, вместо того чтобы прямиком идти на работу. Если я подожду еще 10 минут, то я могу быть у школы как раз в тот момент, когда они только открывают свои двери, тем самым избавив мою жену от неудобств, тем более что школа по пути к выезду из города и это не сильно меня задерживало.
Я вернулся к тому, что я рисовал и добавил следующее:

Выпивая вторую чашку кофе, я встал у окна. Чистое утреннее небо, легкий утренний ветерок подтверждали хороший прогноз на моем смартфоне и я подумал, что поездка в этот раз будет быстрой. Заканчивая свое планирование, я нарисовал примерное время для каждого этапа, которые я нарисовал ранее:

Ожидаемое время поездки было 115 минут (1 час и 55 минут), если я смогу двигаться без лишних остановок. Я ожидал приехать в 8.35, если поеду сразу, или же в 8.55, если придется захватить с собой дочь, чтобы отправить ее в школу и заодно проверить шины.
Но любое планирование перестает быть идеальным после того, как столкнется с реальностью! По каким-то непонятным причинам, многие родители решают оставить своих детей в школе раньше, чем обычно, поэтому я потерял больше 5 минут, по сравнению с тем, что я планировал для своей быстрой поездки. Поняв, что я немного опаздываю, я решил не проверять давление в шинах и ехать сразу.
Я добрался до выезда из города на 5 минут раньше, чем я планировал в самом плохом раскладе дел и все шло хорошо ровно до тех пор, пока где-то между точками B и C в моем плане я не наткнулся на туман, сильно повлиявший на видимость на дороге. Туман снизил мою среднюю скорость? да еще и мешал обгонять медленные, но длинные грузовики. Городской поток в городе я преодолел намного легче, чем обычно и это не заняло больше 10 минут. Через несколько миль на южной дороге туман снизился и я мог спокойно ехать на разрешенной скорости. Но когда я приближался к моей цели, я понял, что впереди идут дорожные работы и это опять отнимет у меня запланированное время. В общем и целом я потратил еще 10 лишних минут на мое путешествие и в конце-концов я опоздал.
Моделируем путешествие
Я понимаю, что большая часть работы с PHP направлена на всякие там интернет-магазины и другие вебсайты. Но PHP может быть прекрасным инструментом для научных исследований, поскольку ему легко обучить непрофессиональных программистов, таких как инженеры и ученые, в отличии от моего любимого Python.
Напишем небольшой код, который поможет мне понять насколько раньше или позже я смогу прибыть на встречу, если пара этапов моего путешествия немного отойдут от намеченного пути. Для начала, можно описать наш путь как он есть:
<?php
class MyTrip
{
protected $departureTime;
protected $meetingTime;
protected $travelTimes;
public function __construct() {
$this->setDepartureTime('0640');
$this->setMeetingTime('0900');
// время потраченное на проезд между этапами
$this->setTravelTimes(array(
'AB' => 17,
'BC' => 17,
'CD' => 36,
'DE' => 9,
'EF' => 15,
'FG' => 15,
'GH' => 6
));
}
// для простоты переведем время в минуты
protected static function convertToMinutes($timeStr) {
return substr($timeStr, 0, 2) * 60 +
substr($timeStr, 2, 2);
}
public function setDepartureTime($timeStr) {
$this->departureTime = self::convertToMinutes($timeStr);
}
public function setMeetingTime($timeStr) {
$this->meetingTime = self::convertToMinutes($timeStr);
}
public function setTravelTimes(array $travelTimes) {
$this->travelTimes = $travelTimes;
}
public checkPlan($stopAtSchool = true, $checkTires = true) {
// ...
}
}
План должен быть осуществимым и подходящим критерием для определения этого будет таким, что сумма всех времен плюс раннее время выезда должна быть меньше или равна времени, на которое назначена моя встреча. Собственно это и определяет метод checkPlan():
<?php
public checkPlan($stopAtSchool = true, $checkTires = true) {
// посчитаем сумму проезда между всеми этапами
$travelTime = array_sum($this->travelTimes);
// добавим задержку, если мне придется отвозить дочь в школу
$schoolDelay = ($stopAtSchool) ? 10 : 0;
// задержка на проверку давления в шинах
$tiresDelay = ($checkTires) ? 10 : 0;
// находим ожидаемое время приезда
$meetingArriveTime = $this->departureTime + $travelTime +
$schoolDelay + $tiresDelay;
// доеду ли я вовремя?
$arriveOnTime = $meetingArriveTime <= $this->meetingTime;
return array($meetingArriveTime, $this->meetingTime,
$arriveOnTime);
}
Все, нам осталось только сделать экземпляр этого класса и проверить:
<?php
$trip = new MyTrip();
print_r($trip->checkPlan());
С учетом настроек по умолчанию, вывод будет таким:
Array
(
[0] => 535
[1] => 540
[2] => 1
)
Я должен прибыть в 535 минут, а встреча назначена на 540 минут. Если перевести на часы, то я прибуду в 8.45, раньше запланированного времени на 15 минут.
Но что на счет возможных задержек? Как их предусмотреть и просчитать?
Метод Монте-Карло или добавляем случайности
В самом простом виде мы можем определить некий безопасный зазор для каждого события и сказать что он может случиться на 10% раньше и на 25% позднее заданного времени. Эти зазоры могут быть случайно добавлены к изначальным задержкам (дочь, давление) и времени между этапами умножением каждого фактора на rand(90,125)/100.
Также можно присвоить 50% вероятность к двум решениям — отвезти дочь в школу и проверить шины. Тут снова поможет rand():
$this->checkTires = rand(1, 100) > 50;
Объединив все это вместе можно определить метод checkPlanRisk() для вычисления решения приеду ли я вовремя или нет, с учетом разных ситуация во время пути:
<?php
public function checkPlanRisk() {
// скорректируем время проезда
$travelTime = 0;
foreach ($this->travelTimes as $t) {
$travelTime += $t * rand(90, 125) / 100;
}
// Решение прихватить с собой дочь
$schoolDelay = 0;
if (rand(1, 100) > 50) {
$schoolDelay = 10 * rand(90, 125) / 100;
}
// и для шин
$tiresDelay = 0;
if (rand(1, 100) > 50) {
$tiresDelay = 10 * rand(90, 125) / 100;
}
// вычисление времени прибытия
$meetingArriveTime = $this->departureTime + $travelTime +
$schoolDelay + $tiresDelay;
// вовремя или же нет?
$arriveOnTime = $meetingArriveTime <= $this->meetingTime;
return array($schoolDelay, $tiresDelay, $meetingArriveTime,
$this->meetingTime, $arriveOnTime);
}
Сейчас встает вопрос прибуду ли я вовремя, принимая во внимание все возможные задержи? Метод Монте-Карло позволяет решить этот вопрос запуском большого количества раз данной задачи и вычисляя «уровень доверия» как отношение времени прибытия вовремя к общему количеству запусков задачи.
Если запустить данный достаточное количество раз и записать как часто я прибуду вовремя, то я смогу определить некоторую вероятность того, что я прибуду как планировал.
<?php
public function runCheckPlanRisk($numTrials) {
$arriveOnTime = 0;
for ($i = 1; $i <= $numTrials; $i++) {
$result = $this->checkPlanRisk();
if ($result[4]) {
$arriveOnTime++;
}
echo "Попыток: " . $i;
echo " Школа: " . $result[0];
echo " Шины: " . $result[1];
echo " Время прибытия: " . $result[2];
if ($result[4]) {
echo " -- Вовремя";
}
else {
echo " -- Опоздание";
}
$confidence = $arriveOnTime / $i;
echo "Уровень доверия: $confidencen";
}
}
Создадим новый экземпляр и сделаем 1000 вычислений друг за другом:
<?php
$trip = new MyTrip();
$trip->runCheckPlanRisk(1000);
После завершения получим прогноз:
Попыток: 1000 Школа: 0 Шины: 11.3 Время прибытия: 530.44 -- Вовремя
Уровень доверия: 0.716
При текущих параметрах, как видно, у меня есть шанс в 72% прибыть на встречу вовремя. Конечно, это просто среднее значение, но и оно имеет право на жизнь.
От себя: скорее всего статья не несет абсолютно ничего нового, заголовок немного желтоват, но мне эта статья показалась забавной. Прочитал давно, а вспомнил с появлением статьи на хабре про Монте-Карло. Может кому-нибудь и пригодится.
