Сегодня предложу Вашему вниманию симпатичный алгоритм, который хоть и придумали совсем недавно (11 лет назад), но «прототипом» послужило счётное устройство с трёхтысячелетней историей.
Авторы
Сортировку презентовали в 2002 году три математика из Университета Окленда, что в Новой Зеландии: Джошуа Дж. Аруланандам (Joshua J. Arulanandham), Кристиан С. Калуд (Cristian S. Calude) и Майкл Дж. Динин (Michael J. Dinneen). Сферы деятельности учёных – дискретная математика, теория чисел, квантовые вычисления, теория информации, комбинаторые алгоритмы.
Не знаю, кому из них троих принадлежит первоначальная идея. Возможно Калуду, который помимо всего прочего преподаёт историю вычислительной математики. Все знают, прародителем счётов в Европе является абак, который из Вавилона перекочевал в Египет, оттуда – в Грецию, из неё – в Рим, из которого – по всей Европе. Внешний вид и принцип действия античного «калькулятора» настолько напоминает поведение этой «простой» сортировки, что её иногда так и называют — «Абаковая сортировка» (Abacus sort).Алгоритм
Предположим, нужно отсортировать набор натуральных чисел. Друг под другом каждое число выложим в виде горизонтального ряда из соответствующего количества шариков. А теперь поглядим на все эти группировки шариков не по горизонталям, а по вертикалям. Сдвинем шарики вниз до упора. Снова переключимся на горизонтали и пересчитаем бусинки в каждом ряду. Получили первоначальный набор чисел, только упорядоченный.Реализация
Bead sort на 30+ языках программирования можно найти здесь. Хотя визуально алгоритм выглядит проще некуда, с точки зрения программной реализации это весьма нетривиальная сортировка.
Вырожденный случай
Таковым является реверсно упорядоченный массив. Максимально возможному количеству шариков придётся рухнуть с наивысших точек.Ограниченная применимость
Метод прежде всего применим к натуральным числам.
Можно сортировать и целые, но это запутаннее – отрицательные числа придётся обрабатывать отдельно от положительных.
Ничего не мешает сортировать и дробные числа, если перед тем привести их к целым (например, всё умножить на 10k, отсортировать, а потом разделить на 10k).
Ну и, конечно, так можно сортировать даже строки, если каждую из них представить в виде целого положительного числа. Но зачем?
Сложность по времени
Их у сортировки аж 4, смотря в каком контексте рассматривать алгоритм.
O(1)
Абстрактный случай, сферическая Bead sort в вакууме. Если представить, что все перемещаемые шарики одновременно сдвигаются и встают на свои места. Это нереализуемая сложность для этой сортировки – ни в теории алгоритмов, ни на практике.
O(√n)
Оценка для физической модели, где бусинки скользят вниз по хорошо смазанным спицам. Время свободного падения пропорционально квадратному корню максимальной высоты, которая в свою очередь кратна n.
O(n)
Шарики, которые ещё не добрались до своих мест, дружно перемещаются на одну позицию вниз за одну итерацию. Об этой сложности уместно говорить в случае физических устройств, реализующих такой способ сортировки, аналоговых или цифровых аппаратных реализаций.
O(S)
S – сумма элементов массива. Каждый шарик перемещается по отдельности, а не перекатываем группы шариков одновременно. Адекватная оценка сложности для реализации на языках программирования.
Сложность по памяти
Оставляет желать лучшего. Bead sort рекордсмен расточительности – расходы на дополнительную память многократно превышают затраты на хранение самого массива и в среднем составляют
Физика
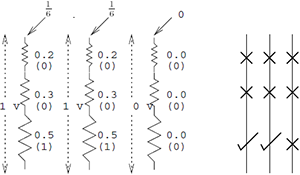
Наличие или отсутствие шариков можно интерпретировать как аналоговое напряжение проходящее через серию электрических резисторов. Стержни, по которым перемещаются шарики – аналоги электрических резисторов, напряжение в которых увеличивается сверху вниз.
Не пинайте за косноязычное использование электротехнических терминов, у меня в школе по физике была
Знатоков электростатики отсылаю за подробностями в этот pdf-документ.
На самом деле
Bead sort – это разновидность сортировки подсчётом. Количество шариков в каждой вертикальной дорожке – это количество элементов в массиве, равных или больших чем порядковый номер вертикали.
Характеристики алгоритма
| Название | Бисерная сортировка (Bead sort); Абаковая сортировка (Abacus sort) | |||
|---|---|---|---|---|
| Авторы | Джошуа Дж. Аруланандам, Кристиан С. Калуд, Майкл Дж. Динин | |||
| Год публикации | 2002 | |||
| Класс | Сортировка распределением | |||
| Устойчивость | Устойчивая | |||
| Сравнения | Без сравнений | |||
| Временная сложность | O(1) | O(√n) | O(n) | O(S) |
| Сложность по памяти | O(n2) | |||
Ссылки
Бисерная сортировка на сайте Оклендского университетаАвторская документация по алгоритму, pdf
Реализация на различных ЯП
Bead sort в анлийской Википедии
Домашние странички авторов:
Джошуа Дж. Аруланандхам
Кристиан С. Калуд
Майкл Дж. Динин
