Доброе время суток, хабров��ане. Сегодня я хочу рассказать вам про рисование симметричной волнистой линии при помощи Кривых Безье, используя только 2 точки.
При создании CAD-систем, часто возникает необходимость рисования не просто прямых линий, а волнистых или ломаных. Так как в обоих случаях линия симметрична относительно прямой, проходящей через начальную и конечные точки, то необходимо вычислить точки, лежащие на параллельных главной прямых. О том, как это сделать, пойдет речь ниже.
Рассмотрим небольшой отрезок. Кривая Безье для этого отрезка должна отдаленно напоминать синусоиду. Хотя и не будет являться ей.
Пусть А — начальная точка, а B — конечная.
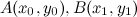
Точка C — середина отрезка АB
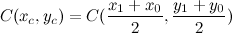
Точки D и E — середины отрезков AC и CB соответственно
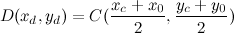
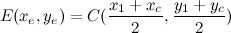
Теперь необходимо получить точки D' и E'. У этих точек одно свойство — они принадлежат отрезкам, которые параллельны AB, но находятся на расстоянии от него.
Рассмотрим вектор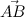 . Необходимо найти два вектора, которые перпендикулярны вектору
. Необходимо найти два вектора, которые перпендикулярны вектору 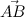 .
.

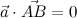
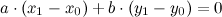
Это обыкновенное линейное уравнение с двумя переменными, которое, как известно, имеет бесконечное множество решений.
Для нахождения первого решения примем за параметр, влияющий на длину вектора.
за параметр, влияющий на длину вектора.
Тогда координаты первого вектора будут равны:
будут равны:
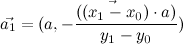
Второй перпендикулярный вектор вычисляется на основе первого.
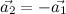
Для получения координат точек D' и E', необходимо прибавить к координатам точки D координаты вектора , а к координатам точки E — координаты вектора
, а к координатам точки E — координаты вектора 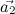 .
.
Зная координаты точек A, D', E' и B, можно построить зигзаг или кривую Безье.
Нарисуем кривую Безье при помощи технологии GDI+ с использованием Windows Forms.
Для начала, опишем класс Vector2
Так же объявим пару переменных для хранения параметров
Теперь напишем код для рисования.
Теперь осталось вызвать этот метод для вашего объекта Graphics.
В результате работы метода должно получиться что-то подобное:

А теперь изменим параметр «Амплитуда» (он же параметр a). Получаем другой результат:

Очевидно, что данный параметр довольно сильно влияет на саму кривую Безье, напоминая силу натяжения нити или амплитуду синусоиды.
Чтобы поставить кривую в зависимость от амплитуды, можно перед вычислением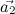 нормализовать вектор
нормализовать вектор  , а потом умножить его на скаляр — на амплитуду.
, а потом умножить его на скаляр — на амплитуду.
Тогда длина перпендикулярных векторов равна амплитуде.
Всем спасибо за внимание.
Предисловие
При создании CAD-систем, часто возникает необходимость рисования не просто прямых линий, а волнистых или ломаных. Так как в обоих случаях линия симметрична относительно прямой, проходящей через начальную и конечные точки, то необходимо вычислить точки, лежащие на параллельных главной прямых. О том, как это сделать, пойдет речь ниже.
Немного математики
Рассмотрим небольшой отрезок. Кривая Безье для этого отрезка должна отдаленно напоминать синусоиду. Хотя и не будет являться ей.
Пусть А — начальная точка, а B — конечная.
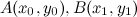
Точка C — середина отрезка АB
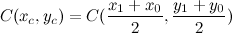
Точки D и E — середины отрезков AC и CB соответственно
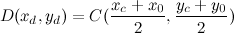
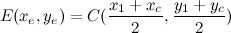
Теперь необходимо получить точки D' и E'. У этих точек одно свойство — они принадлежат отрезкам, которые параллельны AB, но находятся на расстоянии от него.
Рассмотрим вектор
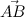 . Необходимо найти два вектора, которые перпендикулярны вектору
. Необходимо найти два вектора, которые перпендикулярны вектору 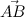 .
. 
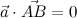
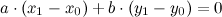
Это обыкновенное линейное уравнение с двумя переменными, которое, как известно, имеет бесконечное множество решений.
Для нахождения первого решения примем
 за параметр, влияющий на длину вектора.
за параметр, влияющий на длину вектора. Тогда координаты первого вектора
 будут равны:
будут равны: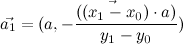
Второй перпендикулярный вектор вычисляется на основе первого.
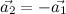
Для получения координат точек D' и E', необходимо прибавить к координатам точки D координаты вектора
 , а к координатам точки E — координаты вектора
, а к координатам точки E — координаты вектора 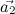 .
.Зная координаты точек A, D', E' и B, можно построить зигзаг или кривую Безье.
Немножко программирования
Нарисуем кривую Безье при помощи технологии GDI+ с использованием Windows Forms.
Для начала, опишем класс Vector2
public class Vector2 { public int X,Y //координаты вектора //конструктор public Vector2(int x, int y) { X=x; Y=y; } }
Так же объявим пару переменных для хранения параметров
int x0,y0;//координаты первой точки int x1,y1;//координаты второй точки int amplitude;//параметр a Pen pen = new Pen(new SolidBrush(Color.Black)); //кисть для рисования простой линии Pen pen2 = new Pen(new SolidBrush(Color.Red));//кисть для рисования кривой.
Теперь напишем код для рисования.
public void Draw(Graphics g) { g.SmoothingMode = SmoothingMode.HighQuality; //включаем Anti-Aliasing // координаты стартовой точки Point mainStart = new Point(x0, y0); // координаты конечной точки Point mainEnd = new Point(x1, y1); //С - середина отрезка AB Point mainCenter0 = new Point((mainStart.X + mainEnd.X) / 2, (mainStart.Y + mainEnd.Y) / 2); //D- середина отрезка AС Point mainCenter1 = new Point((mainStart.X + mainCenter0.X) / 2, (mainStart.Y + mainCenter0.Y) / 2); //E- середина отрезка СB Point mainCenter2 = new Point((mainCenter0.X + mainEnd.X) / 2, (mainCenter0.Y + mainEnd.Y) / 2); //Вектор AB Vector2 lineVector = new Vector2(mainEnd.X - mainStart.X, mainEnd.Y - mainStart.Y ); //вектор a1 Vector2 orthoVector1 = new Vector2( amplitude, -lineVector.X * amplitude / lineVector.Y ); //вектор a2 Vector2 orthoVector2 = new Vector2(-orthoVector1.X, -orthoVector1.Y); //очищаем экран g.Clear(Color.White); //транслируем точку D в точку D' mainCenter1.Offset(orthoVector1.x, orthoVector1.y); //транслируем точку E в точку E' mainCenter2.Offset(orthoVector2.x, orthoVector2.y); //рисуем кривую Безье g.DrawBezier(pen2, mainStart, mainCenter1, mainCenter2, mainEnd); //рисуем простую линию g.DrawLine(pen, mainStart, mainEnd); }
Теперь осталось вызвать этот метод для вашего объекта Graphics.
В результате работы метода должно получиться что-то подобное:

А теперь изменим параметр «Амплитуда» (он же параметр a). Получаем другой результат:

Очевидно, что данный параметр довольно сильно влияет на саму кривую Безье, напоминая силу натяжения нити или амплитуду синусоиды.
Чтобы поставить кривую в зависимость от амплитуды, можно перед вычислением
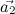 нормализовать вектор
нормализовать вектор  , а потом умножить его на скаляр — на амплитуду.
, а потом умножить его на скаляр — на амплитуду. Тогда длина перпендикулярных векторов равна амплитуде.
Всем спасибо за внимание.
