ЧАСТЬ I . Предварительные сведения о системе и модели.
Проектирование и расчет баллистических характеристик спутниковых систем различного целевого назначения, моделирование процессов движения и функционирования предполагают предварительную оценку возможностей достижения планируемых целевых эффектов такими системами. Целевое назначение сводится в настоящее время к информационному обслуживанию в самом широком смысле целевых объектов (ЦО) бортовой аппаратурой искусственного спутника Земли (ИСЗ). Там где имеют место потоки информации, всегда возникают проблемы, связанные с ее защитой и обеспечением информационной безопасности, со всеми вытекающими отсюда следствиями.
Длительное автономное функционирование приводит к изменению проектных значений баллистических характеристик, прежде всего, структуры спутниковых систем. В свою очередь это требует периодического проведения коррекции значений части характеристик системы. При этом возникает необходимость предварительного их расчета, что возможно при наличии измеренных значений ��араметров движения, как отдельных спутников систем, так и системы в целом. Такие измерения возможны при наличии сети наземных измерительных пунктов (ИП) стационарных или подвижных (сухопутных, морских, воздушных), оборудованных соответствующей измерительной аппаратурой и командными радиосредствами. Здесь рассматривается вероятностный подход к оцениванию и расчету потенциальных возможностей спутниковых систем влиять на информационное обеспечение в глобальном, планетарном масштабе с позиций баллистического построения орбитальной части и размещения объектов, прежде всего измерительных пунктов, наземной части. Вопросы информационной безопасности не рассматриваются.
С каждым ИП и ЦО связывается область пространства (мгновенная зона обслуживания (МЗО)), при попадании в которую ИСЗ, он может быть обслужен или сам выполнить обслуживание ЦО. Процесс обслуживания включает помимо непосредственных измерений баллистических и телеметрических характеристик, прием и передачу целевой информации, связь с ИСЗ, передачу на борт программы коррекции, закладку рабочей программы (РП) функционирования бортовой специальной аппаратуры (БСпА), с учетом обновленных параметров движения и другие операции.
Априори процесс получения требуемых оценок реализовать детерминировано невозможно, так как действие многообразных природных и техногенных факторов приводит к возмущениям параметров. Возмущениям, прежде всего, подвержены параметры движения ИСЗ и, как следствие, характеристики процессов функционирования БСпА. Отсюда возникает потребность в изучении названных явлений как случайных, установления вероятностных законов распределения случайных событий, величин, функций случайных аргументов и случайных функций (полей).
В предлагаемой вниманию читателей работе в рамках модели совместного движения и функционирования орбитальной и наземной частей системы рассматривается взаимодействие пары объектов ИСЗ – ИП. При этом модель включает все основные факторы, формирующие процесс функционирования и порождающие случайность наступления важных системных событий. Из множества системных событий выделяются события взаимодействия ИСЗ с наземными ИП и целевыми объектами.
К числу важнейших факторов, учитываемых в математической модели движения системы, относятся:
– вращение планеты вокруг своей оси (угловая скорость постоянная);
– географическое положение наземного объекта (координаты, радиус МЗО);
– ограниченность времени сеанса взаимодействия (время пребывания объекта в МЗО);
– баллистические характеристики ИСЗ (высота полета Н, наклонение плоскости орбиты).
В математической модели используются (вводятся) упрощающие допущения и предположения:
– планета имеет сферическую форму с радиусом сферы R, гравитационное поле притяжения центральное;
– влияние атмосферы на движение орбитальных объектов не учитывается;
– орбиты движения ИСЗ – круговые, прецессия плоскостей орбит движения не учитывается;
– трассы движения ИСЗ моделируются большими кругами сферы;
– области обслуживания МЗО – конусы с вершиной в центре объекта, линия пересечения, которых со сферой радиуса R+Н проектируется на поверхность сферы планеты плоской окружностью.
В основу модели взаимодействия ИСЗ – ИП положена геометрическая модель элементов системы и кинематические соотношения их перемещения. В трехмерном пространстве плоскости П орбит каждого ИСЗ системы неподвижны, их линии пересечения со сферой планеты – трассы. МЗО наземного объекта (проекция на планету линии пересечения конуса со сферой радиусом R+H) ограничивается сегментом сферической поверхности, отсекаемым плоскостью К. Граница МЗО — окружность L малого круга, «нарисована» на поверхности Земли и движется вместе с Землей. Она периодически пересекается с орбитальной П плоскостью ИСЗ, т.е. сегмент МЗО пересекается трассой, которая также «рисуется» на поверхности Земли для каждого витка ИСЗ заново. На некоторых витках трасса пересекает сегмент, а на некоторых проходит, минуя его. Часть трассы на витке, пересекающем сегмент, от точки входа в сегмент до точки выхода лежит внутри сегмента. Дело в том, что прохождение трассы одного витка спутником занимает время в 15-16 раз меньше длительности суток, т.е.≈ 1,5 часа. Если трасса пересекает сегмент, то время τ пребывания ИСЗ в МЗО пропорционально длине t хорды окружности L, τ = t /2πR.
Действительно, антенна измерительного средства ИП, поворачиваясь, сопровождает движущийся ИСЗ от момента его входа в зону, до момента выхода из нее.
Содержательная постановка задачи
Задача состоит в следующем. Определить вероятность того, что плоскость П орбиты ИСЗ будет рассекать сегмент МЗО при случайном ее положении относительно центра МЗО.
Для определенности модели и удобства рассуждений введем две координатные системы: декартову и сферическую (полярную), начало которых совместим с центром сферической планеты. Положение на сфере любой точки О1 в сферической системе координат будем определять тремя координатами:
– длиной радиуса вектора R;
– долготой λ;
– полярным расстоянием γо = π/2 – φо.
Положительные направления отсчета координат показаны на рис. 1.
Оси ох, оу декартовой системы координат лежат в плоскости экватора планеты, ось ох совпадает с линией его пересечения с меридианом Гринвича, ось оу ��овернута на λ=π/2 и проходит через меридиан с восточной долготой λ=π/2, ось оz дополняет систему координат до правой системы. Формулы перехода от сферических координат к декартовым и обратно имеют вид:
х = Rcosφоcosλо; y = Rcosφоsinλо; z = Rsinφо;
R = [ х2 + y2 +z2]o.5; λо = arctg y/x; φо = arctg z /√ (x2+y2 ).
В декартовой системе координат уравнение плоскости К, формирующей сегмент на сфере планеты, может быть задано в виде
Ах + By + Cz + D = 0,
где А, В, С – компоненты вектора n<3>, нормального к плоскости К, D ≠ 0.
Направляющие косинусы вектора n<3>= <A,B,C>, перпендикулярного плоскости К, определяются по формулам:
cos(α) =A/N; cos(β) = B/N; cos(γ) = C/N; N = [ A2 + B2 +C2]o.5; p = D/N,
где р – расстояние от начала координат до плоскости, причем sign(N) = –sign(D).
Характеристикой сегмента, имеющего в качестве границы окружность L, кроме положения его центра, является радиус r окружности L. Этот радиус может быть определен через радиус R сферы и расстояние (р):
r = Rζc , где ζc = arccos(p/R).
Другими словами, сегмент на сфере может быть задан координатами точки О1(х, у,z) – центра сегмента и углом ζc, либо координатами точки О1(х, у,z) и расстоянием р, либо системой: уравнением сферы и уравнением плоскости К.
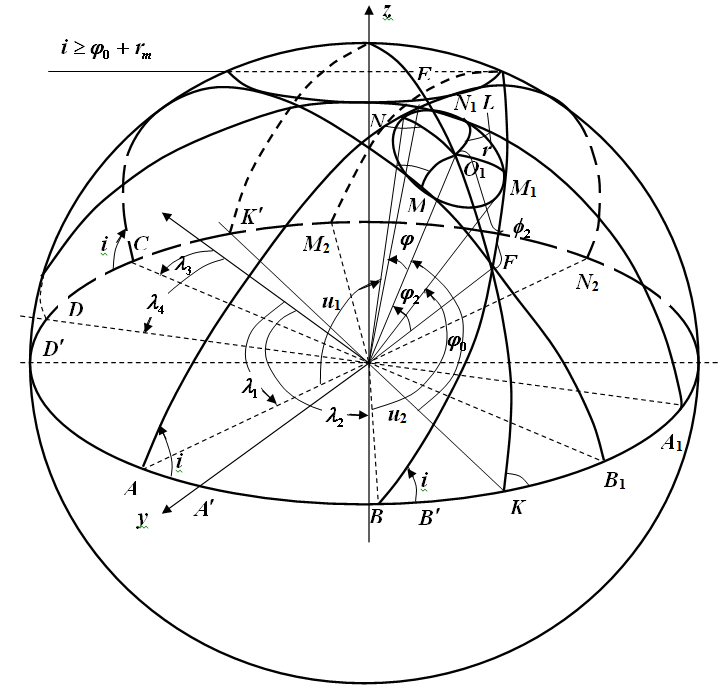
Рисунок 1 Положение трасс ИСЗ с углом наклона i большим широты верхней точки границы МЗО ИП
Плоскость П, проходящую через центр сферы, можно задать аналогичным образом, т. е. общим уравнением плоскости
А1х + B1y + C1z + D1 = 0.
Очевидно, для плоскости П значение D1 = 0. Существует более удобный для моделирования способ задания этой плоскости. В общем случае плоскость П наклонена к плоскости земного экватора, совпадающей с координатной горизонтальной хоу плоскостью, под некоторым углом i, называемым наклонением плоскости орбиты ИСЗ. Линия пересечения плоскостей орбиты П и горизонтальной координатной хоу плоскости называется линией ��злов (восходящего и нисходящего) орбиты.
Положение этой линии в плоскости экватора задается углом λ (географической долготой), отсчитываемым от меридиана Гринвича. В произвольный момент времени линия узлов орбиты некоторого ИСЗ характеризуется случайным значением угла λ. Очевидно, диапазон возможных значений λ определяется интервалом λ ∊ [0, 2π ]. В произвольный момент времени в пределах этого интервала невозможно указать точку, которая имела бы более высокий приоритет относительно всех остальных быть занятой узлом орбиты ИСЗ. Для этого нет ни физических, ни математических, ни каких-либо других обоснований. Следовательно, будем считать вероятностное распределение случайного значения долготы λ для линии узлов орбиты в интервале [0, 2π] равномерным.
Угол наклонения i плоскости орбиты к плоскости экватора будем считать неслучайным. В такой ситуации для плоскости П(i, λ ) удобнее использовать ее представление через эти углы, в виде:
x•tgλ – y + z•ctgi/cosλ = 0.
Каждому случайному положению в пространстве плоскости орбиты ИСЗ П(i, λ ) будет соответствовать одно из возможных значений случайной величины λ.
Прохождение спутником зоны наземного измерительного пункта
Практический интерес для проектировщика спутниковой системы состоит в оценивании возможности проведения сеанса связи ИСЗ и ИП на каждом витке траектории.
Обозначим символом ℬ случайное сложное событие, состоящее в том, что при случайном значении величины долготы λ плоскость П(i, λ), проходящая через центр сферы планеты, пересечет сегмент, ограниченный окружностью L с центром на радиусе-векторе точки О1(х, у,z). Таким образом, в этой части работы задача состоит в определении вероятности наступления случайного события ℬ. Определение вероятности будем выполнять при условии, что λ принимает одно из своих возможных значений. Ясно, что накладываемое условие выполняется всегда. Методы теории вероятностей позволяют определять вероятности одних событий (сложных) через известные вероятности других событий, определенным образом с ними связанных, и вероятности которых заданы или могут быть определены тем или иным способом.
Выполним анализ возможностей реализации события ℬ. Рисунок 1 иллюстрирует геометрию различных ситуаций с рассмотренными ранее объектами, благоприятствующих наступлению моделируемого случайного события ℬ и показывает условия невозможности его наступления.
На рисунке 1 изображена верхняя полусфера планеты и на ней проведены дуги больших и малых кругов. Замкнутая кривая МNN1M1 представляет собой границу МЗО сегмента (окружность L ). Положение центра сегмента О1(х, у,z) характеризуется широтным φо углом и долготным углом λо. Положение плоскости П(i, λ) задается углом наклона i к плоскости экватора, который детерминирован и не меняется в процессе моделирования.
Анализ возможных ситуаций для случайного события ℬ.
Будем различать ситуации, приводящие к различным функциональным зависимостям, порождающим сложное случайное событие ℬ:
Первая ситуация φо+ rm ≤ i. Имеется четыре положения дуг больших кругов АNN2,BM1M2,CMB1,DN1A1, образованных сечением сферы плоскостью П(i, λ) при четырех значениях λ, соответствующих таким положениям плоскости, при которых она касается границы сегмента (окружности L) в четырех точках N,M1, N1, M. Дуга КО1К1 образована сечением сферы плоскостью, перпендикулярной плоскости хоу в меридианном сечении и проходящей через ось оz и точку О1.
В сечении сферы планеты плоскостью экватора хоу показаны линии узлов названных выше плоскостей.
Показаны также углы:
– u1, u2 – между линиями узлов и направлениями в точки касания окружности L, измеряемые дугами АN и ВМ1 соответственно;
– φ1, φ2 – между радиусом-вектором центра сегмента и направлениями в точки пересечения больших кругов, измеряемые дугами О1Е и О1F в меридианном сечении;
– i – угол наклона плоскости П(i, λ) к плоскости хоу.
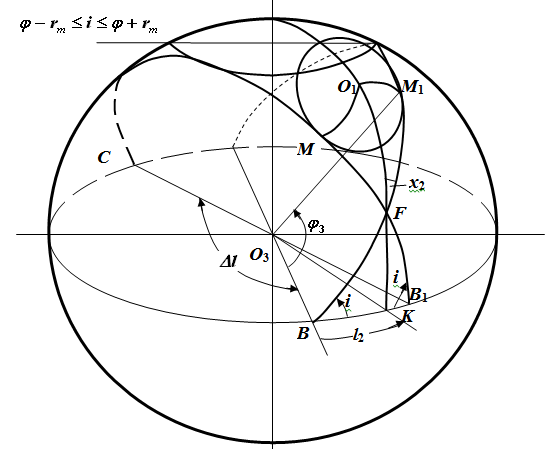
Рисунок 2 Положение трасс ИСЗ с углом наклона i меньшим широты верхней точки границы МЗО ИП
Вторая ситуация φо – rm ≤ i ≤ φо+ rm. Ниже на следующем рисунке 2 изображены два положения плоскости П(i, λ) при двух значениях λ, соответствующих ее касанию окружности L в точках М и М1.
На основе анализа рисунков можно сделать вывод о том, что реализации случайного события ℬ будет соответствовать попадание узловой точки плоскости П(i, λ) в два интервала АВ и СD экваториального круга на верхнем рисунке 1 и в один интервал СВ на нижнем рисунке 2.
Верхнему рисунку соответствует интервал изменения угла i наклона плоскости
φо + ζc ≤ i ≤ π – φо – ζc,
нижнему рисунку – φо – ζc ≤ i ≤ φо + ζc.
Назовем интервалы АВ и СD (на нижнем рисунке СВ) интервалами попадания плоскости П(i, λ) в сегмент или, короче, интервалами попадания. Для каждого фиксированного положения и размера ζc сегмента и угла i наклона плоскости П(i, λ) существуют однозначно определяемые интервалы попадания. Положения, размеры, число интервалов попадания зависят от угла i, координат центра сегмента (φо, λо) и радиуса ζc сегмента.
Из выполненного анализа следует, что случайное событие ℬ сложное и может быть представлено через случайные простые события, состоящие в том, что случайное значение λ будет принадлежать интервалам АВ и СD для ситуации верхнего рисунка и интервалу СВ — для ситуации нижнего рисунка.
Третья ситуация φо — rm > i. Эта ситуация в работе не рассматривается, так как не соответствует наступлению случайного события ℬ. Плоскость движения ИСЗ наклонена столь низко над экватором, что МЗО объектов пересечься с ней не могут.
Представление сложного случайного события ℬ простыми случайными событиями.
Введем обозначения ℬ1 = (λ∊ﺭАВ) и ℬ2 = (λ∊ﺭСD), тогда ℬ = ℬ1+ ℬ2. События ℬ1 и ℬ2 несовместны и, следовательно, при условии, что известен закон распределения долготы узла λ, будет выполняться соотношение Р(ℬ) = Р(ℬ1)+ (ℬ2).
Пусть вероятностное распределение случайной величины λ по большому кругу в плоскости хоу, т.е. в интервале [0, 2π], задано некоторой непрерывной функцией долготы узла – плотностью распределения вероятностей
φλ(λ) = dFλ(λ)/dλ, где Fλ(λ) –функция распределения λ.
Если на числовой оси λ отмечены две дуги граничными точками А, В и С, D, то вероятность попадания λ на интервалы дуг АВ и СD описывается как

Р(ℬ1)=∫φλ(λ)dλ; Р(ℬ2)=∫φλ(λ)dλ определяется интегралами в этих обозначенных пределах, следовательно,
Р(ℬ)=∫φλ(λ)dλ + ∫φλ(λ)dλ, где значения пределов интегрирования пока не определены. Таким образом, для определения вероятностей Р(ℬ) необходимо получить выражения для границ интервалов, характеризуемых длинами дуг λj, j = 1(1)4. Ранее отмечалось, что λj = λj(R, φо, λо, i, ζc ), j = 1(1)4. Найдем в явном виде выражения для длин интервалов попадания.
Обратимся к анализу рисунка 1. Из его рассмотрения можно записать (используем обозначение для дуги ﺭДД):
λ1 = λА = λо – ﺭАК; λ2= λВ = λо – ﺭВК; λ3 = λС = λо – π + ﺭВК; λ4 = λD = λо – π + ﺭАК.
Соотношения для выполнения численных расчетов
Воспользуемся теоремами сферической тригонометрии и получим расчетные формулы для необходимых переменных.
Здесь из прямоугольных сферических треугольников АЕК и ВFК определяются дуги:
ﺭАК = arcsin(tg (φо+ φ1)/tgi); ﺭ BК = arcsin(tg (φо – φ2)/tgi).
Неизвестные величины φ2, φ1, λj = λj(R, φо, λо, i, ζc ), j = 1(1)4 будем определять через известные φо, i, ζc.
Из сферического треугольника NEO1 по теореме синусов можем записать соотношение
sin ζc /sind = sin φ1 /sin90°, где угол d =ےNEO1, из соотношения получаем sind = sin ζc /sin φ1.
По теореме косинусов из сферического треугольника АЕК записываем соотношение
cosi = sindcos(φо+ φ1), из которого для sind получим еще одну зависимость sind =cosi / cos(φо+ φ1).
Найденные разным путем две зависимости приравниваем и выполняем преобразование (переносим влево функции с переменной φ1)
sin ζc /sin φ1 = cosi / cos(φо+ φ1) или cos(φо+ φ1)/ sin φ1 = cosi / sin ζc.
В последнем выражении неизвестной является единственная переменная φ1, которую удалось связать через известные величины, что позволяет выполнить ее преобразование и привести к виду удобному для ее вычисления
cos(φо+ φ1)/ sin φ1 = cos φоctg φ1 – sin φо и далее cos φоctg φ1 – sin φо= cosi /sin ζc откуда
ctg φ1 =( cosi /sin ζc + sinφо )/ cosφо и окончательно,
φ1 = arctg(cos φо sin ζc /(cosi + sinφоsin ζc)).
По аналогии, рассматривая сферические треугольники ОМF и BFK, получаем значение
φ2 = arctg(cos φо sin ζc /(cosi – sinφоsin ζc)).
Подставляя полученные значения φ1 и φ2 в соотношения для долготы λj, j = 1(1)4, можем записать
λ1 = λА = λо – arcsin(tg(φо + arctg(cos φо sin ζc /(cosi + sinφоsin ζc))) /tgi);
λ2 = λB = λо – arcsin(tg(φо – arctg(cos φо sin ζc /(cosi – sinφоsin ζc))) /tgi);
λ3 = λC = λо – π + arcsin(tg(φо – arctg(cos φо sin ζc /(cosi – sinφоsin ζc))) /tgi);
λ4 = λD = λо – π + arcsin(tg(φо + arctg(cos φо sin ζc /(cosi + sinφоsin ζc))) /tgi).
Таким образом, все необходимые данные для расчета вероятности Р(ℬ) определены.
Рассмотрим пример. В приложениях принимается, что закон распределения долготы λj равномерный в интервале [0, 2π]. При этом допущении функция распределения Fλ(λ)и плотность распределения φλ(λ) случайной переменной λ записываются в виде, изображенном под рисунком 3:
Числовые характеристики этих законов распределения определяются из выражений: математическое ожидание m(λ) = π; среднее квадратичное отклонение сигма (λ) = π / √3; дисперсия D(λ) = π2 /3. Для этого случая вероятность попадания ИСЗ в зону обслуживания ИП запишется в виде (с учетом соответствующих пределов интегрирования и суммирования)
Р(ℬ)=∫φλ(λ)dλ +∫φλ(λ)dλ =1/2π ∑|λ2j — λ2j–1|, j = 1,2.
Подставляя в последнее соотношение значения найденных пределов интегрирования и найденные выражения λj, получим окончательное выражение для вероятности попадания ИСЗ в зону измерительного пункта
Р(ℬ) = 1/π ∑(-1)k arcsin(tg(φо –(-1)k arctg(cos φо sin ζc /(cosi –(-1)k sinφоsin ζc))) /tgi), k = 1,2.
Это соотношение позволяет перейти от факта прохождения спутником через зону обслуживания наземного пункта к решению задачи определения времени пребывания ИСЗ в зоне пункта в зависимости от числовых характеристик движения системы (положения долготы восходящего узла орбиты на витке попадания в зону ИП). Эта часть работы автором планируется к публикации в ближайшее время.
Проектирование и расчет баллистических характеристик спутниковых систем различного целевого назначения, моделирование процессов движения и функционирования предполагают предварительную оценку возможностей достижения планируемых целевых эффектов такими системами. Целевое назначение сводится в настоящее время к информационному обслуживанию в самом широком смысле целевых объектов (ЦО) бортовой аппаратурой искусственного спутника Земли (ИСЗ). Там где имеют место потоки информации, всегда возникают проблемы, связанные с ее защитой и обеспечением информационной безопасности, со всеми вытекающими отсюда следствиями.
Длительное автономное функционирование приводит к изменению проектных значений баллистических характеристик, прежде всего, структуры спутниковых систем. В свою очередь это требует периодического проведения коррекции значений части характеристик системы. При этом возникает необходимость предварительного их расчета, что возможно при наличии измеренных значений ��араметров движения, как отдельных спутников систем, так и системы в целом. Такие измерения возможны при наличии сети наземных измерительных пунктов (ИП) стационарных или подвижных (сухопутных, морских, воздушных), оборудованных соответствующей измерительной аппаратурой и командными радиосредствами. Здесь рассматривается вероятностный подход к оцениванию и расчету потенциальных возможностей спутниковых систем влиять на информационное обеспечение в глобальном, планетарном масштабе с позиций баллистического построения орбитальной части и размещения объектов, прежде всего измерительных пунктов, наземной части. Вопросы информационной безопасности не рассматриваются.
С каждым ИП и ЦО связывается область пространства (мгновенная зона обслуживания (МЗО)), при попадании в которую ИСЗ, он может быть обслужен или сам выполнить обслуживание ЦО. Процесс обслуживания включает помимо непосредственных измерений баллистических и телеметрических характеристик, прием и передачу целевой информации, связь с ИСЗ, передачу на борт программы коррекции, закладку рабочей программы (РП) функционирования бортовой специальной аппаратуры (БСпА), с учетом обновленных параметров движения и другие операции.
Априори процесс получения требуемых оценок реализовать детерминировано невозможно, так как действие многообразных природных и техногенных факторов приводит к возмущениям параметров. Возмущениям, прежде всего, подвержены параметры движения ИСЗ и, как следствие, характеристики процессов функционирования БСпА. Отсюда возникает потребность в изучении названных явлений как случайных, установления вероятностных законов распределения случайных событий, величин, функций случайных аргументов и случайных функций (полей).
В предлагаемой вниманию читателей работе в рамках модели совместного движения и функционирования орбитальной и наземной частей системы рассматривается взаимодействие пары объектов ИСЗ – ИП. При этом модель включает все основные факторы, формирующие процесс функционирования и порождающие случайность наступления важных системных событий. Из множества системных событий выделяются события взаимодействия ИСЗ с наземными ИП и целевыми объектами.
К числу важнейших факторов, учитываемых в математической модели движения системы, относятся:
– вращение планеты вокруг своей оси (угловая скорость постоянная);
– географическое положение наземного объекта (координаты, радиус МЗО);
– ограниченность времени сеанса взаимодействия (время пребывания объекта в МЗО);
– баллистические характеристики ИСЗ (высота полета Н, наклонение плоскости орбиты).
В математической модели используются (вводятся) упрощающие допущения и предположения:
– планета имеет сферическую форму с радиусом сферы R, гравитационное поле притяжения центральное;
– влияние атмосферы на движение орбитальных объектов не учитывается;
– орбиты движения ИСЗ – круговые, прецессия плоскостей орбит движения не учитывается;
– трассы движения ИСЗ моделируются большими кругами сферы;
– области обслуживания МЗО – конусы с вершиной в центре объекта, линия пересечения, которых со сферой радиуса R+Н проектируется на поверхность сферы планеты плоской окружностью.
В основу модели взаимодействия ИСЗ – ИП положена геометрическая модель элементов системы и кинематические соотношения их перемещения. В трехмерном пространстве плоскости П орбит каждого ИСЗ системы неподвижны, их линии пересечения со сферой планеты – трассы. МЗО наземного объекта (проекция на планету линии пересечения конуса со сферой радиусом R+H) ограничивается сегментом сферической поверхности, отсекаемым плоскостью К. Граница МЗО — окружность L малого круга, «нарисована» на поверхности Земли и движется вместе с Землей. Она периодически пересекается с орбитальной П плоскостью ИСЗ, т.е. сегмент МЗО пересекается трассой, которая также «рисуется» на поверхности Земли для каждого витка ИСЗ заново. На некоторых витках трасса пересекает сегмент, а на некоторых проходит, минуя его. Часть трассы на витке, пересекающем сегмент, от точки входа в сегмент до точки выхода лежит внутри сегмента. Дело в том, что прохождение трассы одного витка спутником занимает время в 15-16 раз меньше длительности суток, т.е.≈ 1,5 часа. Если трасса пересекает сегмент, то время τ пребывания ИСЗ в МЗО пропорционально длине t хорды окружности L, τ = t /2πR.
Действительно, антенна измерительного средства ИП, поворачиваясь, сопровождает движущийся ИСЗ от момента его входа в зону, до момента выхода из нее.
Содержательная постановка задачи
Задача состоит в следующем. Определить вероятность того, что плоскость П орбиты ИСЗ будет рассекать сегмент МЗО при случайном ее положении относительно центра МЗО.
Для определенности модели и удобства рассуждений введем две координатные системы: декартову и сферическую (полярную), начало которых совместим с центром сферической планеты. Положение на сфере любой точки О1 в сферической системе координат будем определять тремя координатами:
– длиной радиуса вектора R;
– долготой λ;
– полярным расстоянием γо = π/2 – φо.
Положительные направления отсчета координат показаны на рис. 1.
Оси ох, оу декартовой системы координат лежат в плоскости экватора планеты, ось ох совпадает с линией его пересечения с меридианом Гринвича, ось оу ��овернута на λ=π/2 и проходит через меридиан с восточной долготой λ=π/2, ось оz дополняет систему координат до правой системы. Формулы перехода от сферических координат к декартовым и обратно имеют вид:
х = Rcosφоcosλо; y = Rcosφоsinλо; z = Rsinφо;
R = [ х2 + y2 +z2]o.5; λо = arctg y/x; φо = arctg z /√ (x2+y2 ).
В декартовой системе координат уравнение плоскости К, формирующей сегмент на сфере планеты, может быть задано в виде
Ах + By + Cz + D = 0,
где А, В, С – компоненты вектора n<3>, нормального к плоскости К, D ≠ 0.
Направляющие косинусы вектора n<3>= <A,B,C>, перпендикулярного плоскости К, определяются по формулам:
cos(α) =A/N; cos(β) = B/N; cos(γ) = C/N; N = [ A2 + B2 +C2]o.5; p = D/N,
где р – расстояние от начала координат до плоскости, причем sign(N) = –sign(D).
Характеристикой сегмента, имеющего в качестве границы окружность L, кроме положения его центра, является радиус r окружности L. Этот радиус может быть определен через радиус R сферы и расстояние (р):
r = Rζc , где ζc = arccos(p/R).
Другими словами, сегмент на сфере может быть задан координатами точки О1(х, у,z) – центра сегмента и углом ζc, либо координатами точки О1(х, у,z) и расстоянием р, либо системой: уравнением сферы и уравнением плоскости К.

Рисунок 1 Положение трасс ИСЗ с углом наклона i большим широты верхней точки границы МЗО ИП
Плоскость П, проходящую через центр сферы, можно задать аналогичным образом, т. е. общим уравнением плоскости
А1х + B1y + C1z + D1 = 0.
Очевидно, для плоскости П значение D1 = 0. Существует более удобный для моделирования способ задания этой плоскости. В общем случае плоскость П наклонена к плоскости земного экватора, совпадающей с координатной горизонтальной хоу плоскостью, под некоторым углом i, называемым наклонением плоскости орбиты ИСЗ. Линия пересечения плоскостей орбиты П и горизонтальной координатной хоу плоскости называется линией ��злов (восходящего и нисходящего) орбиты.
Положение этой линии в плоскости экватора задается углом λ (географической долготой), отсчитываемым от меридиана Гринвича. В произвольный момент времени линия узлов орбиты некоторого ИСЗ характеризуется случайным значением угла λ. Очевидно, диапазон возможных значений λ определяется интервалом λ ∊ [0, 2π ]. В произвольный момент времени в пределах этого интервала невозможно указать точку, которая имела бы более высокий приоритет относительно всех остальных быть занятой узлом орбиты ИСЗ. Для этого нет ни физических, ни математических, ни каких-либо других обоснований. Следовательно, будем считать вероятностное распределение случайного значения долготы λ для линии узлов орбиты в интервале [0, 2π] равномерным.
Угол наклонения i плоскости орбиты к плоскости экватора будем считать неслучайным. В такой ситуации для плоскости П(i, λ ) удобнее использовать ее представление через эти углы, в виде:
x•tgλ – y + z•ctgi/cosλ = 0.
Каждому случайному положению в пространстве плоскости орбиты ИСЗ П(i, λ ) будет соответствовать одно из возможных значений случайной величины λ.
Прохождение спутником зоны наземного измерительного пункта
Практический интерес для проектировщика спутниковой системы состоит в оценивании возможности проведения сеанса связи ИСЗ и ИП на каждом витке траектории.
Обозначим символом ℬ случайное сложное событие, состоящее в том, что при случайном значении величины долготы λ плоскость П(i, λ), проходящая через центр сферы планеты, пересечет сегмент, ограниченный окружностью L с центром на радиусе-векторе точки О1(х, у,z). Таким образом, в этой части работы задача состоит в определении вероятности наступления случайного события ℬ. Определение вероятности будем выполнять при условии, что λ принимает одно из своих возможных значений. Ясно, что накладываемое условие выполняется всегда. Методы теории вероятностей позволяют определять вероятности одних событий (сложных) через известные вероятности других событий, определенным образом с ними связанных, и вероятности которых заданы или могут быть определены тем или иным способом.
Выполним анализ возможностей реализации события ℬ. Рисунок 1 иллюстрирует геометрию различных ситуаций с рассмотренными ранее объектами, благоприятствующих наступлению моделируемого случайного события ℬ и показывает условия невозможности его наступления.
На рисунке 1 изображена верхняя полусфера планеты и на ней проведены дуги больших и малых кругов. Замкнутая кривая МNN1M1 представляет собой границу МЗО сегмента (окружность L ). Положение центра сегмента О1(х, у,z) характеризуется широтным φо углом и долготным углом λо. Положение плоскости П(i, λ) задается углом наклона i к плоскости экватора, который детерминирован и не меняется в процессе моделирования.
Анализ возможных ситуаций для случайного события ℬ.
Будем различать ситуации, приводящие к различным функциональным зависимостям, порождающим сложное случайное событие ℬ:
Первая ситуация φо+ rm ≤ i. Имеется четыре положения дуг больших кругов АNN2,BM1M2,CMB1,DN1A1, образованных сечением сферы плоскостью П(i, λ) при четырех значениях λ, соответствующих таким положениям плоскости, при которых она касается границы сегмента (окружности L) в четырех точках N,M1, N1, M. Дуга КО1К1 образована сечением сферы плоскостью, перпендикулярной плоскости хоу в меридианном сечении и проходящей через ось оz и точку О1.
В сечении сферы планеты плоскостью экватора хоу показаны линии узлов названных выше плоскостей.
Показаны также углы:
– u1, u2 – между линиями узлов и направлениями в точки касания окружности L, измеряемые дугами АN и ВМ1 соответственно;
– φ1, φ2 – между радиусом-вектором центра сегмента и направлениями в точки пересечения больших кругов, измеряемые дугами О1Е и О1F в меридианном сечении;
– i – угол наклона плоскости П(i, λ) к плоскости хоу.

Рисунок 2 Положение трасс ИСЗ с углом наклона i меньшим широты верхней точки границы МЗО ИП
Вторая ситуация φо – rm ≤ i ≤ φо+ rm. Ниже на следующем рисунке 2 изображены два положения плоскости П(i, λ) при двух значениях λ, соответствующих ее касанию окружности L в точках М и М1.
На основе анализа рисунков можно сделать вывод о том, что реализации случайного события ℬ будет соответствовать попадание узловой точки плоскости П(i, λ) в два интервала АВ и СD экваториального круга на верхнем рисунке 1 и в один интервал СВ на нижнем рисунке 2.
Верхнему рисунку соответствует интервал изменения угла i наклона плоскости
φо + ζc ≤ i ≤ π – φо – ζc,
нижнему рисунку – φо – ζc ≤ i ≤ φо + ζc.
Назовем интервалы АВ и СD (на нижнем рисунке СВ) интервалами попадания плоскости П(i, λ) в сегмент или, короче, интервалами попадания. Для каждого фиксированного положения и размера ζc сегмента и угла i наклона плоскости П(i, λ) существуют однозначно определяемые интервалы попадания. Положения, размеры, число интервалов попадания зависят от угла i, координат центра сегмента (φо, λо) и радиуса ζc сегмента.
Из выполненного анализа следует, что случайное событие ℬ сложное и может быть представлено через случайные простые события, состоящие в том, что случайное значение λ будет принадлежать интервалам АВ и СD для ситуации верхнего рисунка и интервалу СВ — для ситуации нижнего рисунка.
Третья ситуация φо — rm > i. Эта ситуация в работе не рассматривается, так как не соответствует наступлению случайного события ℬ. Плоскость движения ИСЗ наклонена столь низко над экватором, что МЗО объектов пересечься с ней не могут.
Представление сложного случайного события ℬ простыми случайными событиями.
Введем обозначения ℬ1 = (λ∊ﺭАВ) и ℬ2 = (λ∊ﺭСD), тогда ℬ = ℬ1+ ℬ2. События ℬ1 и ℬ2 несовместны и, следовательно, при условии, что известен закон распределения долготы узла λ, будет выполняться соотношение Р(ℬ) = Р(ℬ1)+ (ℬ2).
Пусть вероятностное распределение случайной величины λ по большому кругу в плоскости хоу, т.е. в интервале [0, 2π], задано некоторой непрерывной функцией долготы узла – плотностью распределения вероятностей
φλ(λ) = dFλ(λ)/dλ, где Fλ(λ) –функция распределения λ.
Если на числовой оси λ отмечены две дуги граничными точками А, В и С, D, то вероятность попадания λ на интервалы дуг АВ и СD описывается как

Р(ℬ1)=∫φλ(λ)dλ; Р(ℬ2)=∫φλ(λ)dλ определяется интегралами в этих обозначенных пределах, следовательно,
Р(ℬ)=∫φλ(λ)dλ + ∫φλ(λ)dλ, где значения пределов интегрирования пока не определены. Таким образом, для определения вероятностей Р(ℬ) необходимо получить выражения для границ интервалов, характеризуемых длинами дуг λj, j = 1(1)4. Ранее отмечалось, что λj = λj(R, φо, λо, i, ζc ), j = 1(1)4. Найдем в явном виде выражения для длин интервалов попадания.
Обратимся к анализу рисунка 1. Из его рассмотрения можно записать (используем обозначение для дуги ﺭДД):
λ1 = λА = λо – ﺭАК; λ2= λВ = λо – ﺭВК; λ3 = λС = λо – π + ﺭВК; λ4 = λD = λо – π + ﺭАК.
Соотношения для выполнения численных расчетов
Воспользуемся теоремами сферической тригонометрии и получим расчетные формулы для необходимых переменных.
Здесь из прямоугольных сферических треугольников АЕК и ВFК определяются дуги:
ﺭАК = arcsin(tg (φо+ φ1)/tgi); ﺭ BК = arcsin(tg (φо – φ2)/tgi).
Неизвестные величины φ2, φ1, λj = λj(R, φо, λо, i, ζc ), j = 1(1)4 будем определять через известные φо, i, ζc.
Из сферического треугольника NEO1 по теореме синусов можем записать соотношение
sin ζc /sind = sin φ1 /sin90°, где угол d =ےNEO1, из соотношения получаем sind = sin ζc /sin φ1.
По теореме косинусов из сферического треугольника АЕК записываем соотношение
cosi = sindcos(φо+ φ1), из которого для sind получим еще одну зависимость sind =cosi / cos(φо+ φ1).
Найденные разным путем две зависимости приравниваем и выполняем преобразование (переносим влево функции с переменной φ1)
sin ζc /sin φ1 = cosi / cos(φо+ φ1) или cos(φо+ φ1)/ sin φ1 = cosi / sin ζc.
В последнем выражении неизвестной является единственная переменная φ1, которую удалось связать через известные величины, что позволяет выполнить ее преобразование и привести к виду удобному для ее вычисления
cos(φо+ φ1)/ sin φ1 = cos φоctg φ1 – sin φо и далее cos φоctg φ1 – sin φо= cosi /sin ζc откуда
ctg φ1 =( cosi /sin ζc + sinφо )/ cosφо и окончательно,
φ1 = arctg(cos φо sin ζc /(cosi + sinφоsin ζc)).
По аналогии, рассматривая сферические треугольники ОМF и BFK, получаем значение
φ2 = arctg(cos φо sin ζc /(cosi – sinφоsin ζc)).
Подставляя полученные значения φ1 и φ2 в соотношения для долготы λj, j = 1(1)4, можем записать
λ1 = λА = λо – arcsin(tg(φо + arctg(cos φо sin ζc /(cosi + sinφоsin ζc))) /tgi);
λ2 = λB = λо – arcsin(tg(φо – arctg(cos φо sin ζc /(cosi – sinφоsin ζc))) /tgi);
λ3 = λC = λо – π + arcsin(tg(φо – arctg(cos φо sin ζc /(cosi – sinφоsin ζc))) /tgi);
λ4 = λD = λо – π + arcsin(tg(φо + arctg(cos φо sin ζc /(cosi + sinφоsin ζc))) /tgi).
Таким образом, все необходимые данные для расчета вероятности Р(ℬ) определены.
Рассмотрим пример. В приложениях принимается, что закон распределения долготы λj равномерный в интервале [0, 2π]. При этом допущении функция распределения Fλ(λ)и плотность распределения φλ(λ) случайной переменной λ записываются в виде, изображенном под рисунком 3:
Числовые характеристики этих законов распределения определяются из выражений: математическое ожидание m(λ) = π; среднее квадратичное отклонение сигма (λ) = π / √3; дисперсия D(λ) = π2 /3. Для этого случая вероятность попадания ИСЗ в зону обслуживания ИП запишется в виде (с учетом соответствующих пределов интегрирования и суммирования)
Р(ℬ)=∫φλ(λ)dλ +∫φλ(λ)dλ =1/2π ∑|λ2j — λ2j–1|, j = 1,2.
Подставляя в последнее соотношение значения найденных пределов интегрирования и найденные выражения λj, получим окончательное выражение для вероятности попадания ИСЗ в зону измерительного пункта
Р(ℬ) = 1/π ∑(-1)k arcsin(tg(φо –(-1)k arctg(cos φо sin ζc /(cosi –(-1)k sinφоsin ζc))) /tgi), k = 1,2.
Это соотношение позволяет перейти от факта прохождения спутником через зону обслуживания наземного пункта к решению задачи определения времени пребывания ИСЗ в зоне пункта в зависимости от числовых характеристик движения системы (положения долготы восходящего узла орбиты на витке попадания в зону ИП). Эта часть работы автором планируется к публикации в ближайшее время.
