Пишем конвертер для генератора мелодий от Nokia 3310

Любителям всего старого, но безумно интересного, добрый вечер!

Помните такой телефон — Nokia 3310? Разумеется, помните! А такую штуку как синтезатор мелодий в нем? Тоже помните, отлично. А по старым, теплым и ламповым мелодиям скучаете? Вот и я скучаю. А еще мне на глаза попался сайтик с более чем сотней нотных листов для этого редактора. И что я должен был оставить эту прелесть без внимания? Нет уж. Что я сделал? Правильно! Взял и написал точно такой же генератор мелодий, который позволяет на выходе получить Wave — файл с мелодией. Интересно, что из этого получилось? Тогда прошу под кат.

Nokia Composer был встроен в целую кучу телефонов, подобных Nokia 3310. Кроме 7 нот, он позволял записать 5 диезов, указать октаву и длительность в частях. А еще были ноты, которые не звучали — паузы. То есть «нота» в Composer'e была действительно нотой.

Сама запись ноты для Composer'a выглядела так:



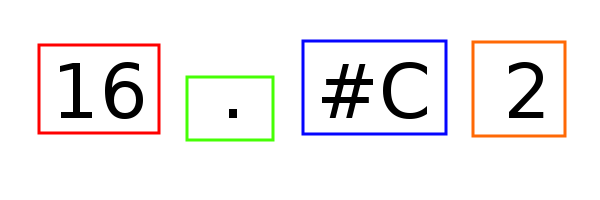
То есть, в начале идет длительность (в частях от целой), затем могла присутствовать точка, удлиняющая звучание в полтора раза, сама нота в буквенном обозначении, и октава. При этом после паузы октава не указывается (логично?), а длительность указывается ровно так же, как и для нормальной ноты.

Ладно, наговорились.

Давайте напишем скрипт, который будет принимать ноту, как она есть и возвращать кортеж параметров.

(пишем на Python 2.7, да)

def Parse_Tone(Note):
	Note = Note.upper()
	if Note.find("-") == -1:
		try:
			(Duration, Octave) = re.findall(r"[0-9]+", Note)
		except:
			pass
	else:
		Duration = re.findall(r"[0-9]+", Note)[0]
		Octave = 1
	Tone = re.findall(r"[A-Z,#,-]+", Note)[0]
	Duration = int(Duration)
	Octave = int(Octave)
	if Note.find(".") != -1:
		Duration = Duration/1.5
	
	return (32/Duration, Tone, Octave)

Во! То есть, сначала мы переводим ее в ВЕРХНИЙ РЕГИСТР, а затем — с помощью регулярных выражений разбираем на составляющие. Отдельно проверяем наличие точки (увеличиваем в 1.5 раза) и учитываем паузу.

Готото!
Теперь если передать функции, например, 16C2, на выходе получим (2, C, 2) то есть длительность в долях, ноту и октаву.

Что? Откуда взялось число 32? Это просто
Оригинальный Nokia Composer позволял установить длительность ноты как 1/32 «полной» ноты. При этом для него существуют еще и 1/16, 1/8, 1 / 4, 1 /2 и 1 длительности. То есть каждая следующая длительность отличается от предыдущей ровно в 2 раза. Тогда мы можем сделать вот что:

Возьмем 1/32 ноты как «единичную ноту». Тогда 1/16 — это уже 2 единичных ноты, 1/8 — 4 и так далее. Тогда мы можем взять и поделить 32 на полученную длительность.

С этим разобрались. Теперь осталось понять, как мы будем все это дело превращать в Wav — файл.

Если очень грубо — в Wave файле, кроме заголовка записаны напряжения, которые подаются на динамик. Если чуть точнее — части напряжений от максимального. То есть, если в двухбайтовом фрейме записано число 32765 — это означает, что нужно подать максимальное напряжение. Изменяя уровни напряжений с течением времени, мы можем добиться колебаний мембраны динамика. А если эти колебания будут в нужном нам диапазоне… Правильно! Мы услышим звук определенной частоты.

Теперь, о том, как это сделать.

Давайте напряжем память и… вспомним школьный курс физики! Примерно ту часть, в которой говорится о гармонических колебаниях.

Если очень просто: гармонические колебания — тип колебаний, колеблющаяся величина которых изменяется по закону синуса (ну или косинуса, как хотите)



Общая формула этого безобразия выглядит как:



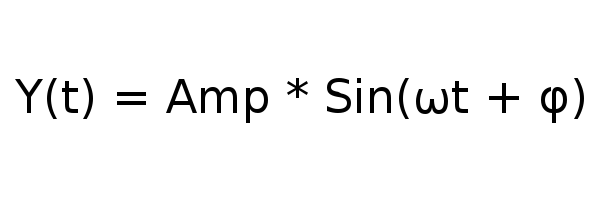
При этом циклическая частота это



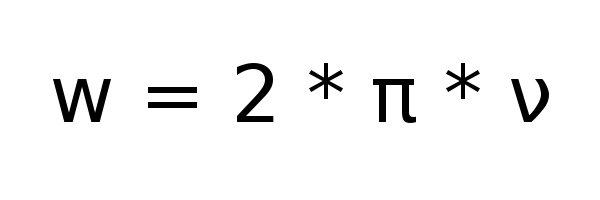
Вспомнили? Отлично! Теперь надо понять — зачем.

Раз уж звук мы решили задавать как изменение напряжения на динамике, то изменения это будем задавать как синусоиду с нужной нам циклической частотой (кстати, самый наглядный способ формирования звука). При этом формула для расчета амплитуды текущего фрейма будет выглядеть как

Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))

Откуда все это взялось? Рассказываю.

32765 — Фрейм у нас двухбайтовый, поэтому максимальное значение амплитуды ровно 32765. VOL — переменная, задающая громкость. Изменяется в диапазоне от 0 (полная тишина) до 1 (орет как на площади)

6.28 — это всего-навсего 2*Pi. Можно каждый раз высчитывать, но мы ж не звери.

FREQ — А это то, ради чего все и затевалось — нужная нам частота.

i/44100 — время, относительно начала отсчета. Почему мы делим на 44100? А потому что это частота дискретизации выходного файла (ну это я так придумал. Можно и меньше. Качество будет ниже). За секунду проходит 44100 отсчетов, поэтому и делим. Надеюсь, получилось объяснить

Ну вот. Один фрейм мы задавать научились. Теперь нужно сделать так, чтобы это все работало. То есть, помимо частоты задать еще и длительность.

А раз уж частота фиксированная… Ага! Обернем в цикл.

Вот в такой.

for i in range(0,TIME/10*441):
		Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))
		Frames.append(Result)

Опять непонятности. Откуда взялось TIME/10*441? Из моего воображения. Нет, серьезно. Это я так решил, что минимальное время звучания — 0.001 секунда. Как я уже говорил — один отсчет (при данной частоте дискретизации) это 1/44100 секунды. Соответственно, 0.001 секунда это 44.1 отсчета. А 44.1 = 441/10. А если надо задать N миллисекунд… домножим, ага. Вот мы и получаем то, что написали (TIME — это как раз таки время в миллисекундах, да)

Так ну и обернем все это дело функцию, надеюсь никто не против?

def Append_Freq(VOL,FREQ, TIME):
	for i in range(0,TIME/10*441):
		Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))
		Frames.append(Result)

Во! Теперь мы можем генерировать звук абсолютно любой частоты.

Осталось записать то, что получилось в wave — файл.

Для работы с Wave в Python (по крайней мере в 2.7) есть прелестный модуль с незабываемым названием — Wave. А для работы со всяческими структурами — struct (вообще, до определенного момента, Python — безумно логичный язык).

После некоторых плясок с бубном и прочих извращений получилась вот такая функция:

def Write_Wave(Name):
	File = wave.open(Name, 'w')
	File.setparams((1, 2, 44100, 0, 'NONE', 'not compressed'))
	Result = []
	for frame in Frames:
		Result.append(pack('h', frame))
	for Each in Result:
		File.writeframes(Each)

(про нее рассказывать не буду, потому как во — первых все понятно, а во — вторых — не будем отдаляться от темы)

Ну вот. Теперь можно сгенерировать звук!
Пробуем.

Frames = []
Append_Freq(1, 4000, 5000)
Write_Wave('Sound.wave')

Полная громкость, 4 килогерца, 5 секунд.
Посмотрим что получилось?

Вот так это звучит:

5000Hz.wav

А вот так выглядит:



Ну, в общем — то, что хотели, то и получили. Звук, правда довольно неприятный.

Кстати, если мне не изменяет память, что в старой библиотеке для Turbo Pascal звук задавался не синусоидой, а меандром. На самом деле достаточно просто изменять напряжение на динамике. Просто синусоида симпатичнее, чем меандр или пила.

Ну вот. Теперь у нас есть функция генерирующая звук нужной частоты и длительности и функция, записывающая то, что мы наделали в настоящий файл.

Теперь нужно научиться записывать ноты.

Чистая (инструментально не окрашенная) нота — это звук определенной частоты.

Диез чистой ноты — звук, с частотой на полтона выше чистой ноты

Бе — моль — звук с частотой на полтона ниже чистой ноты. Бе — моли оригинальный Composer (еще помните, что мы там хотели написать? Отлично!) задавать не дает, поэтому с бе — молями работать не будем. Ну их.

Октава — если упрощенно, это множитель частоты ноты. То есть частота Ре второй октавы вдвое выше той же Ре первой октавы.

Найдем на просторах интернета таблицу нот и их частот



И сделаем из нее словарь.

Вот такой:

Notes = {"-" : 0 ,"C" : 261.626, "#C" : 277.183, "D" : 293.665, "#D" : 311.127, "E": 329.628, "#E" : 349.228, "F" : 349.228, "#F" : 369.994, "G" : 391.995, "#G" : 415.305, "A" : 440.000, "#A" : 466.164, "B" : 493.883, "#B" : 523.251}

(Вообще, наверно, правильнее писать C#, а не #C, но как правило все мелодии для Composer'a указывались именно в таком формате)

А теперь напишем еще одну функцию, генерирующую звук определенной ноты

def Append_Note(VOL, TIME, NOTE, OCTAVE):
	for i in range(0,int(TIME/10.0*441)):
		FREQ = Notes[NOTE]*OCTAVE
		Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))
		Frames.append(Result)
		
		#making clear sound
	if (abs(math.sin(6.28*FREQ*i/44100))>0.01):
		while (abs(math.sin(6.28*FREQ*i/44100))>0.01):
			Result = (32765*VOL*math.sin(6.28*FREQ*i/44100))
			Frames.append(Result)
			i+=1

Так, тут надо еще кое — что дорассказать.

С первой частью все понятно — значение нужной частоты берется из словаря, домножается на октаву и пишется в список.

Зачем нужна вторая?

Очень просто. Если желаемая длительность не кратна периоду синусоиды, то в момент времени T1 на динамик может подаваться большое напряжение, а в T1+1 уже ничего подаваться не будет. На мой медвежий слух, это звучит как внезапно оборвавшаяся фраза убитого товарища — неприятно. Поэтому мы доводим нашу синусоиду до ближайшего нуля. При высокой частоте дискретизации заметно это будет мало, а на слух будет выглядеть как та же обрывающаяся фраза товарища, если на глазах мертвеющий (но вопящий) товарищ падает в колодец. Тоже не Бог весть что, но для генерации Нокиевских мелодий сгодится.

Теперь осталось написать функцию, которая будет принимать список нот и поэлементно скармливать его генератору.

def Append_Notes(VOL, LIST, BPM):
	for Each in LIST:
		(Duration, Tone, Octave) = Parse_Tone(Each)
		try:
			Append_Note(VOL, int(Duration*1000*7.5/BPM), Tone, Octave)	
		except:
			print "Ошибка! Не могу обработать %s" %Each
		Append_Note(0, int(250*7.5/BPM), "-", 1)

Приблизительно вот так.

Снова что — то непонятно? Это нормально, я тоже ничего не понимаю, сейчас разберемся.

BPM — это количество ударов в минуту. Грубо говоря, это «скорость игры». Это самое BPM равно количеству четвертных нот за одну минуту. То есть одна четвертная нота должна играться 60/BPM секунд. А поскольку, мы решили, что длительность единичной ноты у нас это 1/32 — это значение равно 60/32*4/BPM = 7.5/BPM. Звучит одна четвертная нота ровно 1000 миллисекунд (композиторы почему — то так придумали), а потом этот результат домножается еще и на количество таких 1/32 нот.

Когда функция отработает в списке Frame окажется готовый файл, который останется только записать.

Ну и поскольку мне лень писать GUI я люблю консольные интерфейсы, напишем обработчик последовательности нот, который принимает эту последовательность, BPM и имя выходного файла в списке аргументов и скармливает функции Append_Notes()

def MakeTune():

	if (len(Arguments)!=3):
		print 'ERROR!\n	USAGE:\n	Composer "Notes" BMP FileName\nExample:\n	Composer "16c2 16#a1 4c2 2f1 16#c2 16c2 8#c2 8c2 2#a1 16#c2 16c2 4#c2 2f1 16#a1 16#g1 8#a1 8#g1 8g1 8#a1 2#g1 16g1 16#g1 2#a1 16#g1 16#a1 8c2 8#a1 8#g1 8g1 4f1 4#c2 1c2 16c2 16#c2 16c2 16#a1 1c2" 120 Music.wave'
		return 1

	List = Arguments[0].split(' ')

	BPM = int(Arguments[1])

	OutFile = Arguments[2]
	
	print "\nFile information:\n\n	Note number: %s\n	Tempo: %s BPM\n\nGeneration of amplitude..." % (len(List), BPM)

	Append_Notes(1, List, BPM)
	print "\nOk!\n\nWriting Wave File..."
	Write_Wave(OutFile)
	File = open(OutFile,'rb').read()
	Size = len(File)
	print "\n	File size: %.2f MB\n	Duration: %.2f c. \n\nAll Done." % (Size/1024.0/1024, Size/44100/2)

Вот и все.

Теперь осталось только передать программе исходные данные и забрать готовую мелодию.

Попробуем?

Ноты

16c2 16#a1 4c2 2f1 16#c2 16c2 8#c2 8c2 2#a1 16#c2 16c2 4#c2 2f1 16#a1 16#g1 8#a1 8#g1 8g1 8#a1 2#g1 16g1 16#g1 2#a1 16#g1 16#a1 8c2 8#a1 8#g1 8g1 4f1 4#c2 1c2 16c2 16#c2 16c2 16#a1 1c2

Вгоняем в генератор…



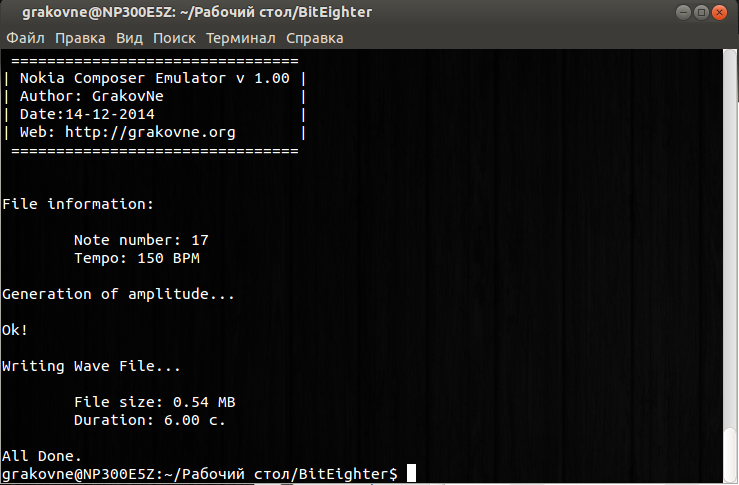
И забираем результат:

output.wav

По — моему неплохо.

Еще примеров? Легко!

Гимн СССР
Под небом голубым
Осень
Рождественская мелодия (из оригинального 3310)

Хотите сами писать? Попробуйте!

Вот ноты

4d1 4g1 8g1 8a1 8g1 8#f1 4e1 4c1 4e1 4a1 8a1 8b1 8a1 8g1 4#f1 4d1 4d1 4b1 8b1 8c2 8b1 8a1 4g1 4e1 8d1 8d1 4e1 4a1 4#f1 2g1

Вот темп: 200

Пропустите через генератор и посмотрите что получится (А кто-то может и на глаз узнает).

Скрипт генератора

Надеюсь, вам понравилось!

Искренне Ваш, слушающий монофонического Моцарта, GrakovNe