Я любитель популярной компьютерной карточной игры Hearthstone, разработанной компанией Blizzard Entertainment. Однажды я задался вопросом: «Можно ли исходя только из правил, описывающих динамику переходов игрока между уровнями при проигрыше\выигрыше партии, получить статистику распределения игроков по достигнутому ими уровню?»
Несмотря на то, что в сети есть огромное количество сайтов и wiki, посвящённых Hearthstone, поверхностный поиск результатов не дал. На глубокий поиск было жаль времени, поэтому я решил задачу «на коленке». Полагаю, это решение может стать темой для занятия в школьном математическом кружке.
В рейтинговом турнире Hearthstone есть 25 уровней и специальный уровень «Легенда». Уровни состоят из подуровней — т.н. «звёзд», причём на разных уровнях число подуровней отличается:
Таким образом линейка уровней в рейтинге (далее — линейка) состоит из 96 подуровней (включая «Легенду»):
Рисунок 1
Новый игрок стартует в рейтинге с 25-го уровня. За выигрыш партии игрок получает «звезду» (иногда – две), т.е. повышает свой подуровень на 1 (или 2 соответственно).
На линейке есть 4 диапазона, в которых отличаются правила изменения уровня игрока при выигрыше\проигрыше партии:
Таблица 1
Очевидно, что «Трамплин» служит для вовлечения новых игроков, так как на «трамплине» есть только награда, но нет наказания за пора��ение. Кроме того, понятно, что население «трамплина» экспоненциально быстро «вымирает», поскольку правила неизбежно выталкивают игрока с «трамплина» в диапазон «Гонки с ускорением». Вероятность остаться на «трамплине» после 18 игр составляет ~29%, а после 27 игр – менее 1,5%.
«Гонка с ускорением» помогает игрокам с высоким мастерством и хорошими колодами быстрее добраться до «Нормальной гонки», где и начинается настоящее «рубилово». Ну и, наконец, «Легенда» — загончик для топовых игроков.
Мне хотелось найти 2 зависимости:
Первой мыслью было написать программу на JS, моделирующую множество игроков, уровни которых в результате взаимодействия меняются по вышеприведённым правилам. По недолгом размышлении об объёме требуемого JS кода я решил, что электронные таблицы отлично подходят для решения этой задачи.
Идея решения следующая:
Пусть некоторый прямоугольный диапазон размером 96*1 (например диапазон Source!$C$3:$C$98 в прилагаемых файлах) представляет распределение количества игроков по линейке. Тогда, используя правила из таблицы 1, легко получить распределение, описывающее состояние, после того, как каждый игрок сыграл одну игру. Правила из таблицы 1 расположены в диапазоне Source!$D3:$D$98. Если «протащить» эти правила на нужное количество столбцов, то получившая таблица будет представлять изменение распределения игроков по уровням со «временем». Время в данном случае в кавычках потому, что здесь оно измеряется в «сыгранных играх».
Я начал с Open Office Calc, который всем хорош, но 3-D графики «из коробки» в нём выглядят убого (возможно, я просто не умею их готовить). В итоге решение реализовано на MS Excel и лежит здесь. Вариант для Open Office Calc там же — вполне функциональный, за исключением отсутствия 3-D графиков и отсутствия интерактивности в 2-D графиках.
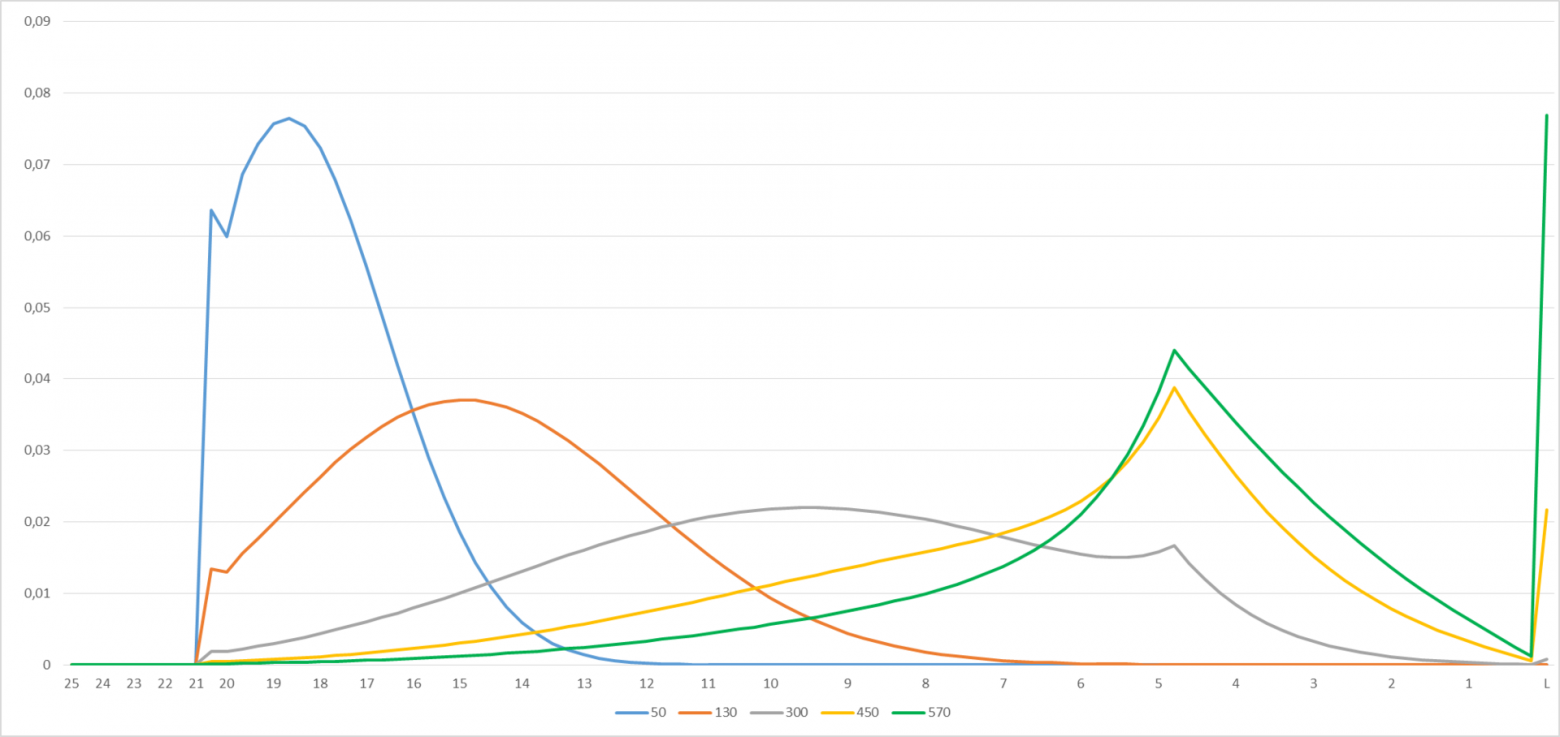
Рисунок 2
Приведённые графики описывают вероятность получить тот или иной уровень для игрока, стартовавшего с 25 уровня и сыгравшего 50, 130, 300, 450 или 570 игр соответственно. В Excel график интерактивный – можно поиграться с числами слева от диаграммы на вкладке «Interface», при этом графики (Рисунок 2) будут меняться.
В 3-D эволюция вероятности получения определённого уровня выглядит очень симпатично:
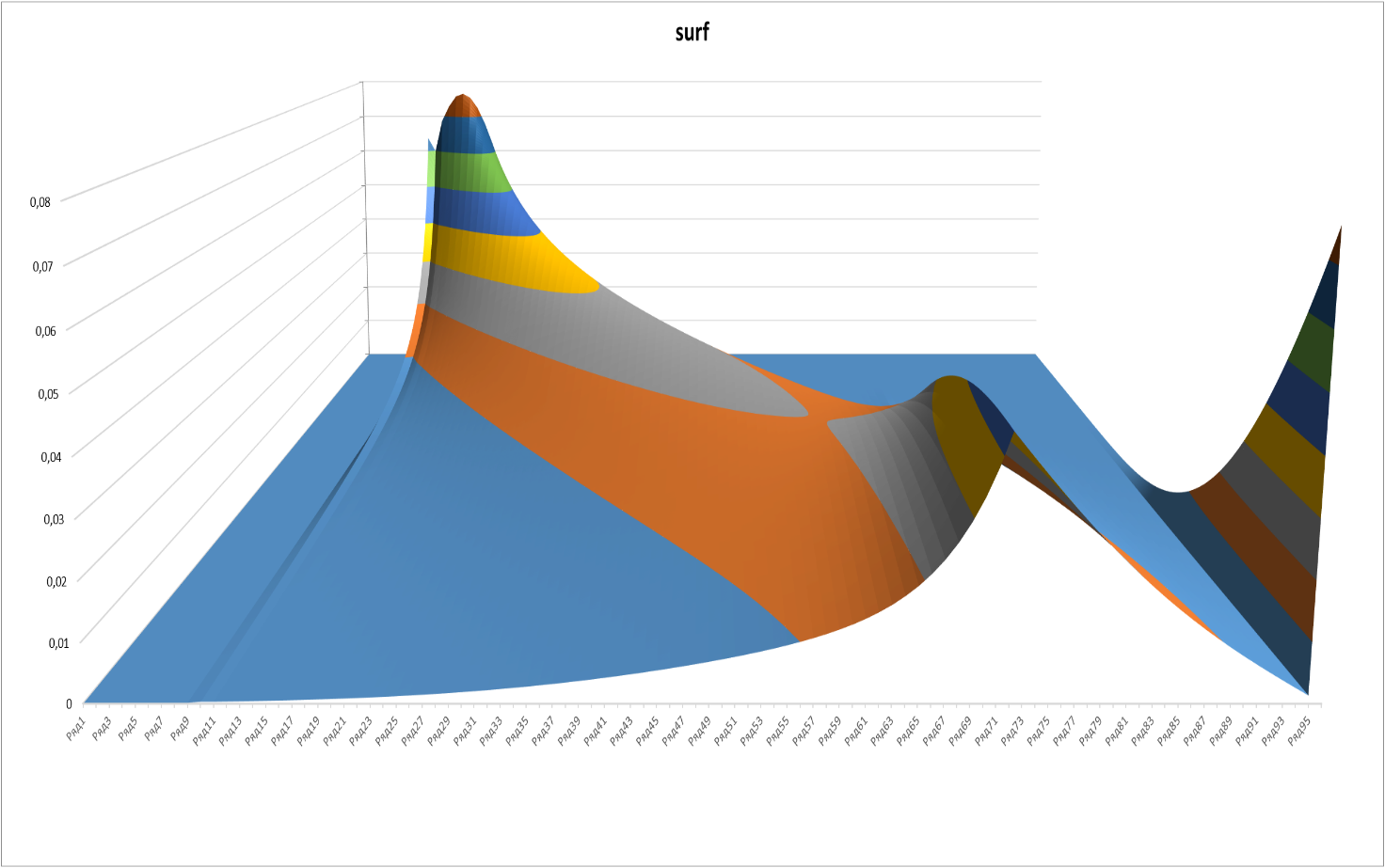
Рисунок 3
Здесь приведён срез с теми же минимальной и максимальной «временными» границами (50 и 570 игр), что и на рисунке 2.
Тот же график с другого ракурса:
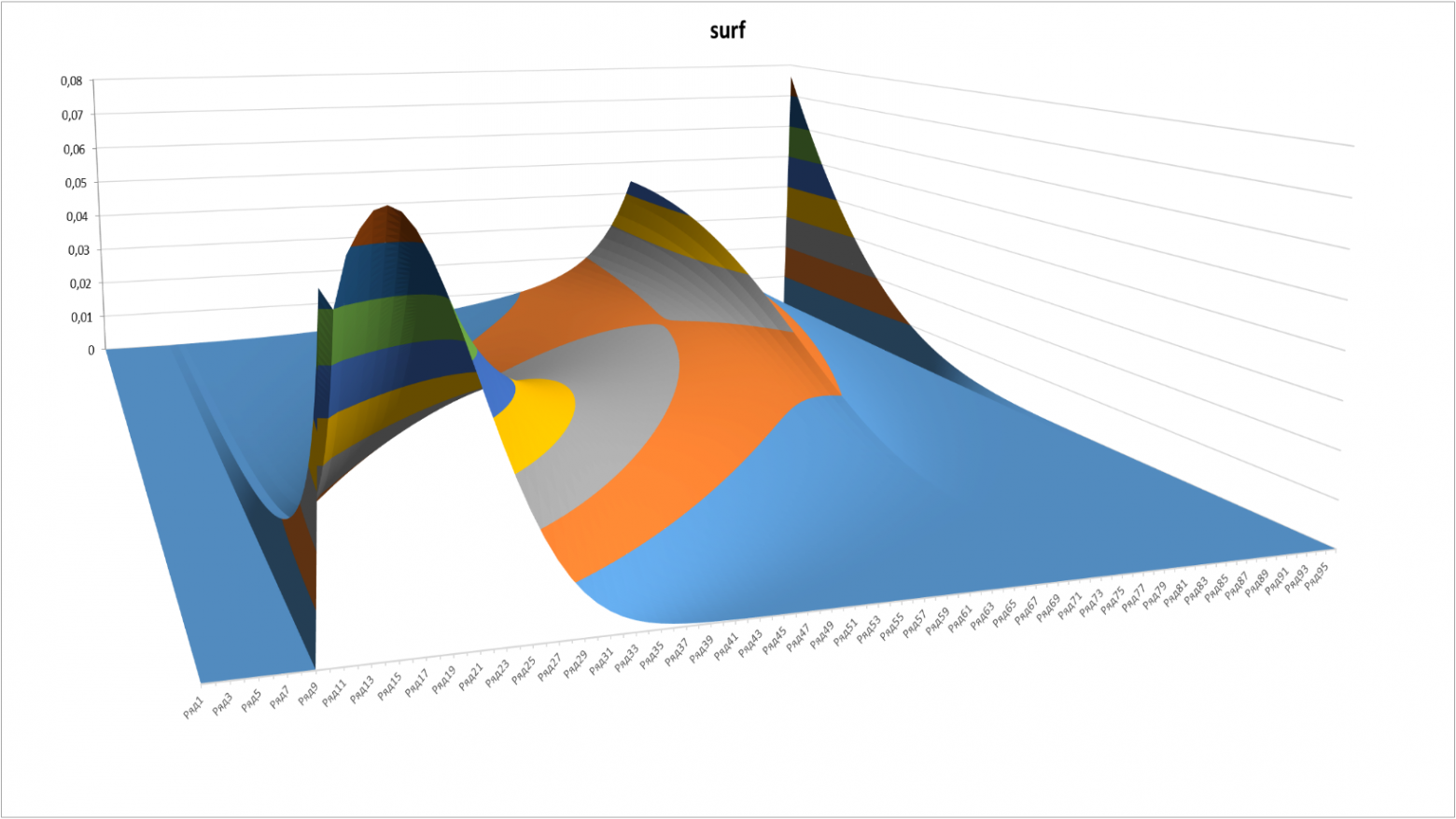
Рисунок 4
Несколько неожиданным выглядит появление «ребра» на графиках в точке, соответствующей уровню 5 и 2 «звезды» (72-й подуровень по порядку). Данная точка является последней, на которую действует возможность попадания «с ускорением» после 3+ побед подряд.
Если посмотреть правила для 71 – 72 подуровней, то они выглядят следующим образом:
71 =1/8*C69+C70*3/8+0,5*C72
72 =1/8*C70+C71*1/2+0,5*C73
Здесь СNN- количество игроков на подуровне NN на предыдущем шаге:
— первый член обеспечивает «ускоренный перенос» с уровня «текущий -2»;
— второй член обеспечивает обычный переход при победе на уровне «текущий -1»;
— третий член обеспечивает переход с вышележащего уровня при поражении.
Разница в 1/8 в коэффициенте при втором члене обусловлена тем, что, начиная с 5-го уровня (он же 71-й порядковый подуровень), независимо от числа побед подряд, повышение подуровня проходит только на 1, т.е. даже если победа на 71-м подуровне была для игрока 3-й, он перейдёт лишь на 72-й подуровень.
Эта небольшая на первый взгляд добавка приводит к тому, что «поток игроков» на 72-й подуровень чуть выше среднего, соответственно чуть выше будет и поток игроков с 72-го подуровня в его окрестности, т.е. эффект повышения потока игроков на 72-й подуровень самоусиливается, что и приводит к появлению этого замечательного ребра.
Очевидно, что игроки различаются по количеству игр, которые они играют за одно и то же время. Более увлечённые игроки играют больше, казуальные – меньше.
Для вычисления модельного распределения игроков по уровням необходимо знать функцию распределения игроков по количеству сыгранных ими игр.
Введём обозначения:
Тогда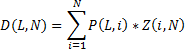
Сразу скажу, что данных о функции Z(i, N) у меня нет. Но можно немного поспекулировать на эту тему.
Единственное, что пришло мне в голову: «20% людей выпивают 80% пива». Возможно, «20% игроков в Hearthstone играют 80% игр»? То есть гипотеза состоит в том, что распределение игроков по количеству сыгранных игр – это дискретное распределение Парето, или, более точно – распределение Ципфа (см. en.wikipedia.org/wiki/Zipf%27s_law).
Введём обозначения:
Тогда распределение Ципфа со степенным показателем s:
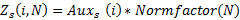
Посмотрим на графики искомой функции D (L,N) в предположении, что распределение игроков по количеству сыгранных игр это распределение Ципфа с показателем степени 1.
Здесь и на следующем графике отображена D (L,N) в моменты «времени» N с 50 до 700.
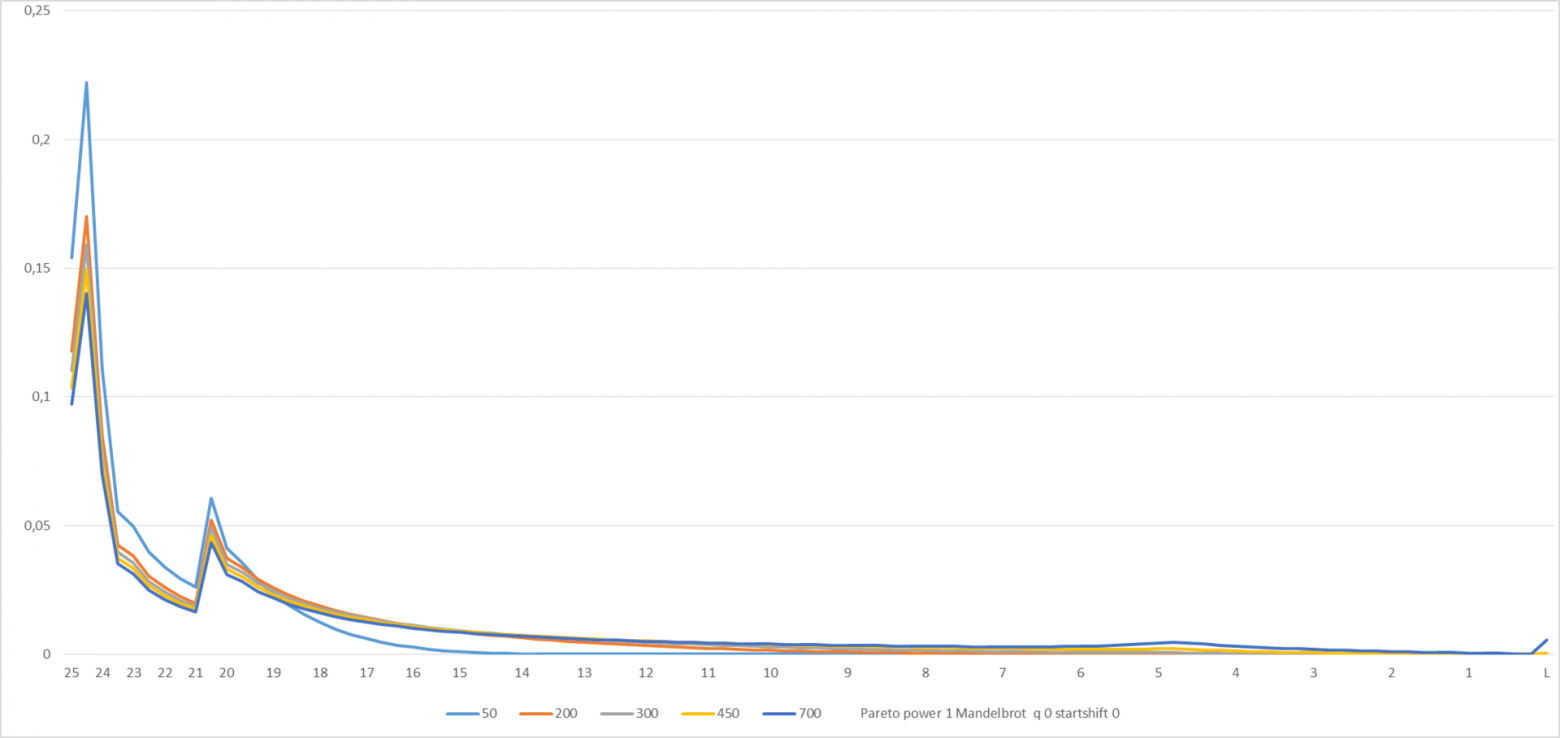
Рисунок 5
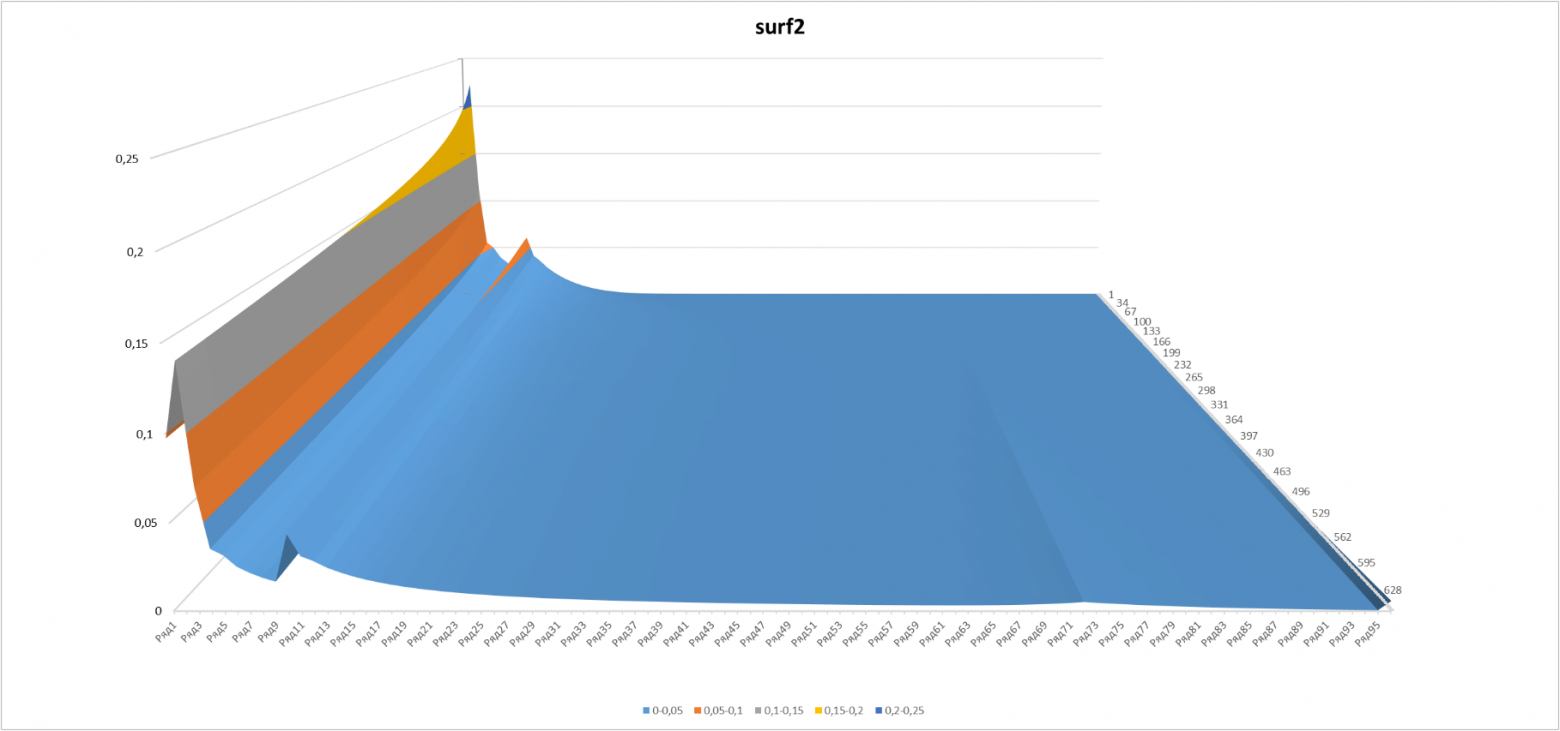
Рисунок 6
Выглядит довольно уродливо, хотя и понятно почему – значительная часть игроков в соответствии с распределением Ципфа осталась на «трамплине». Ну что ж, спекулировать – так по полной. Построим модифицированное распределение Ципфа-Мандельброта (см. en.wikipedia.org/wiki/Zipf%E2%80%93Mandelbrot_law).
1. Заменим вспомогательную функцию
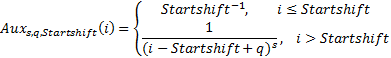
Идея введения целочисленного параметра Startshift состоит в следующем: начало «действия» стандартного поведения распределения Ципфа сдвинуто на Startshift шагов.
Действительно, представляется неправдоподобным, что игрок, прошедший все трудности обучения и только вышедший на рейтинговые игры, с высокой вероятностью бросит играть после одной-двух рейтинговых игр. Можно предположить, что начало «действия» распределения Ципфа примерно совпадает с началом трудностей в продвижении в рейтинге, т.е. с моментом, когда вероятность покинуть «трамплин» превысит ½ (это означает, что startshift=18). Кроме того, из определения вспомогательной функции следует, что общее число игроков «случайно зашедших в Hearthstone» (т.е. сыгравших ≤Startshift игр) совпадает с числом игроков на максимуме распределения. Всё это, конечно, чистая спекуляция, но почему бы не посмотреть, что получится?
Параметр Мандельброта q введён без какого-либо обоснования, на всякий случай.
2. Нормировочный множитель (для момента «времени» N)
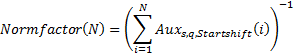
Тогда модифицированное распределение со степенным показателем s, параметром Мандельброта q и параметром «стартового сдвига» Startshift:
Посмотрим, что получается при параметрах, приведённых в нижней части графика:
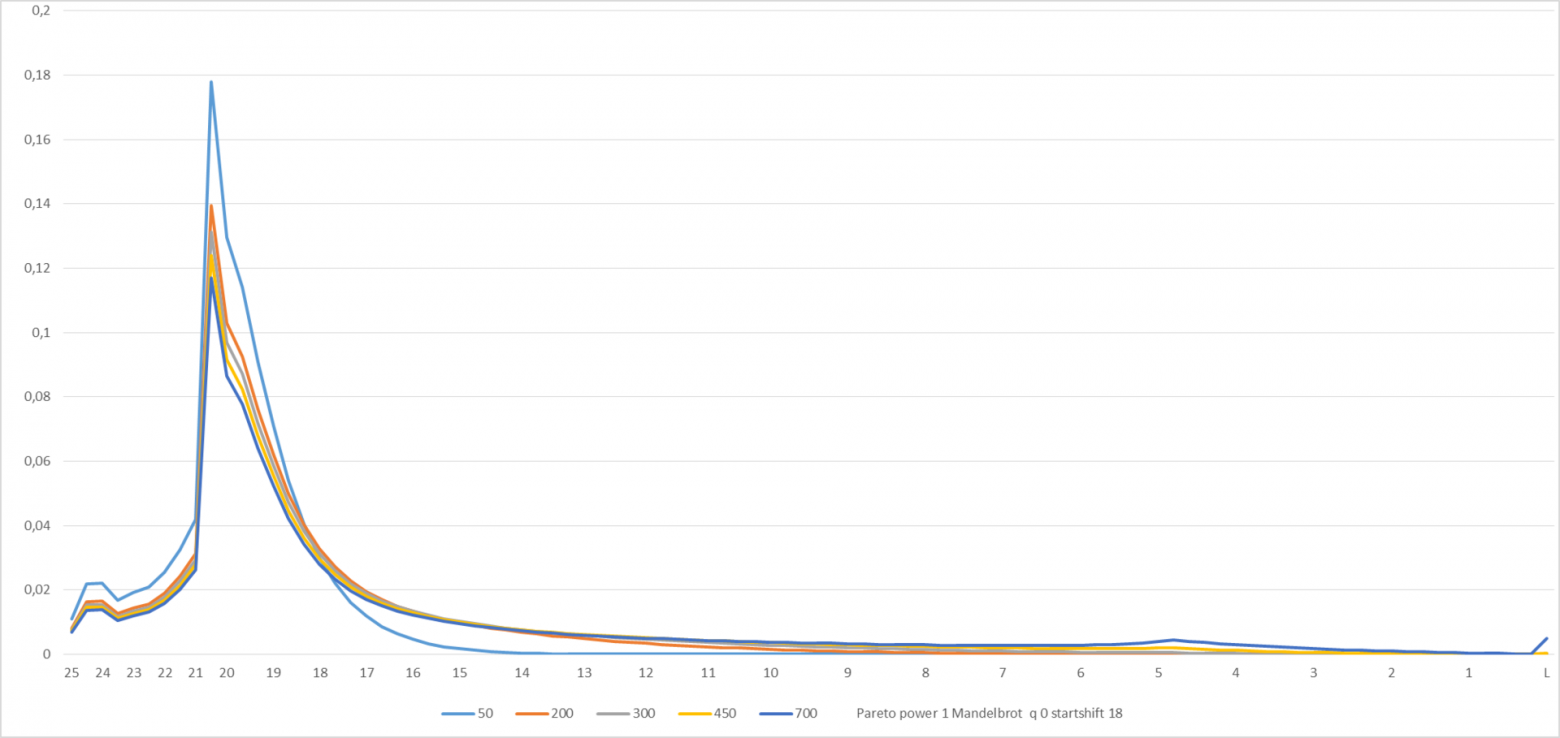
Рисунок 7
Для ручных экспериментов график в Excel сделан интерактивным – можно поиграться с параметрами распределения и отображаемыми «временами» слева от диаграммы на вкладке «Interface», при этом графики (Рисунок 7 и Рисунок 8) будут меняться.
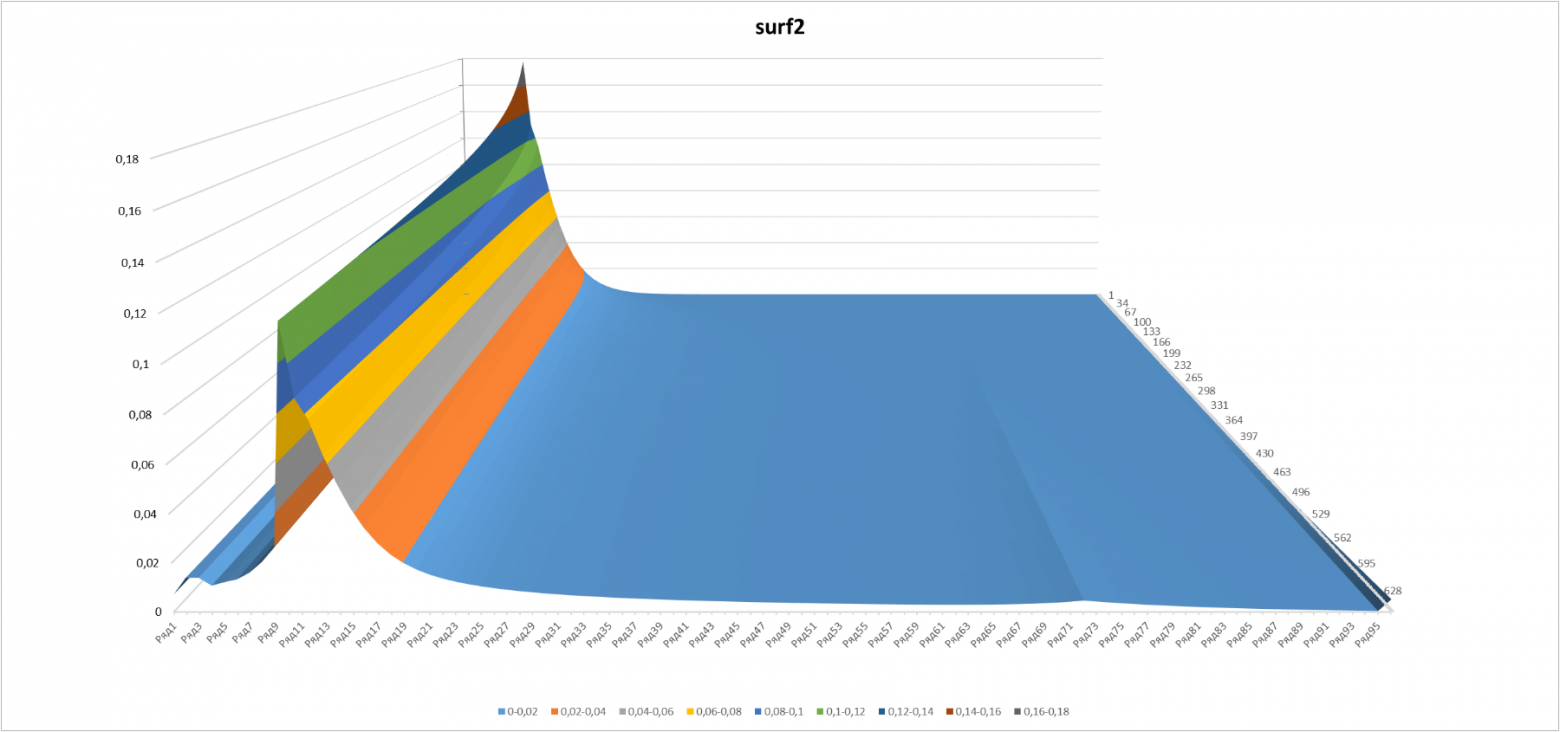
Рисунок 8
И наконец, последний рывок на сегодня. Попробуем подобрать параметры распределения, используя «реальные» данные (http://www.reddit.com/r/hearthstone/comments/23ed7l/how_good_are_you_at_constructed_ladder/). Это результаты какой-то симуляции, детали которой мне неизвестны, неясно, в частности, в какой момент «времени» N проведено измерение и т.д. Это единственное, что я нашёл. Но я не очень старался искать. Надеюсь, читатели статьи подскажут источник более релевантных данных.
Итерационная обработка данных надстройкой solver и ручная подгонка дали следующие значения параметров распределения: s=1,19; q=0,287; Startshift =110. Startshift ожидаемо большой, поскольку в исходных данных симуляции отсутствует информация о населении уровней 25-21, т.е. «трамплин», очевидно, не симулировался.
Финальные картинки:
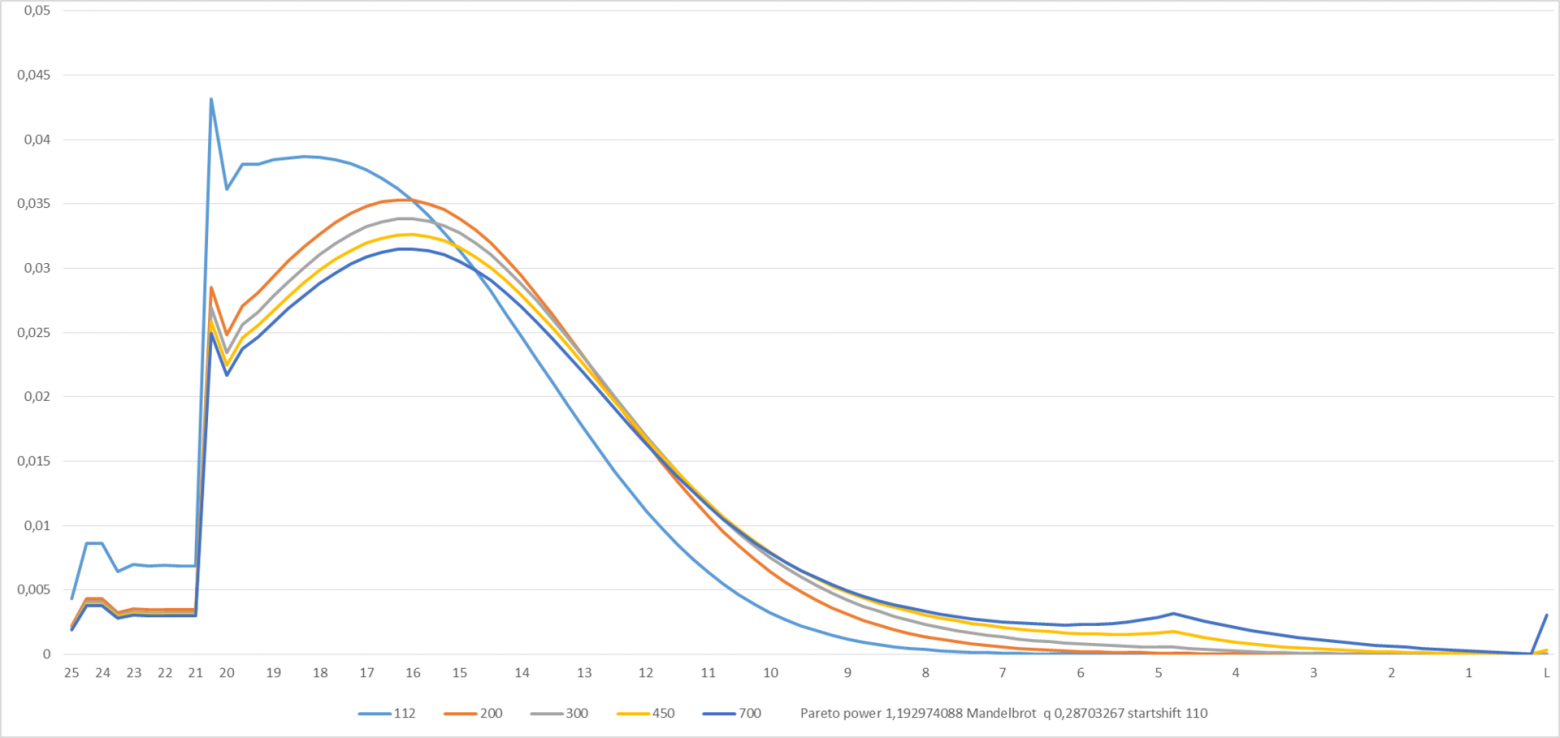
Рисунок 9
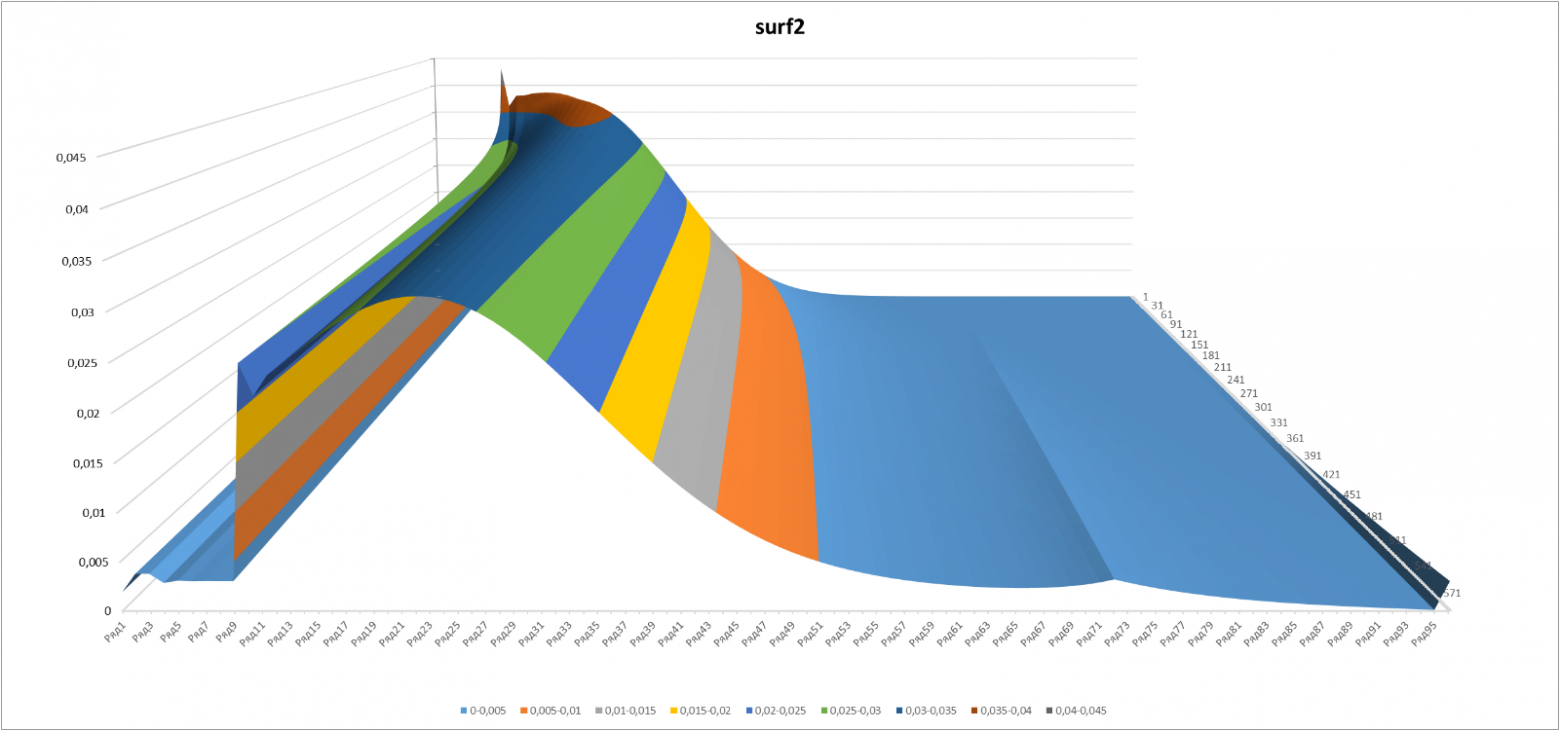
Рисунок 10
В заключение повторюсь, что задача, которую я стал решать из чистого любопытства, показалась мне неплохой темой для занятия в школьном математическом кружке. Считаю важным для будущих инженеров и учёных умение использовать для решения внезапно возникающих задач все имеющиеся подручные инструменты: бумагу и карандаш, электронные таблицы, пакет «WOLFRAM MATHEMATICA». Надеюсь, настоящий пример применения электронной таблицы будет кому-нибудь полезен.
При желании преподаватель может проложить мостики от этой задачи ко множеству тем.
Навскидку:
Также можно придумать какие-нибудь расширения к данной задаче. Например, такие:
1) Когда заканчивается сезон, то игроки, достигнувшие определённых уровней в прошлом сезоне, получают некоторую фору. Например, при окончании сезона на уровне 4 игрок получает 21 «звезду», т.е. стартует в новом сезоне не с 25 уровня, а с уровня 17.**- он же 21-й порядковый подуровень (см. Рисунок 1). Уверен, что соответствующие цифры, описывающие зависимость размера форы от достигнутого уровня, легко найти в сети.
Вопросы:
2) Придумать какую-нибудь внятную теорию для вычисления функции Z(i, N).
Несмотря на то, что в сети есть огромное количество сайтов и wiki, посвящённых Hearthstone, поверхностный поиск результатов не дал. На глубокий поиск было жаль времени, поэтому я решил задачу «на коленке». Полагаю, это решение может стать темой для занятия в школьном математическом кружке.
Описание задачи
В рейтинговом турнире Hearthstone есть 25 уровней и специальный уровень «Легенда». Уровни состоят из подуровней — т.н. «звёзд», причём на разных уровнях число подуровней отличается:
- Уровни с 25 по 21 состоят из 2-х подуровней;
- Уровни с 20 по 16 состоят из 3-х подуровней;
- Уровни с 15 по 11 состоят из 4-х подуровней;
- Уровни с 10 по 1 состоят из 5-и подуровней;
- На «Легенде» подуровней нет.
Таким образом линейка уровней в рейтинге (далее — линейка) состоит из 96 подуровней (включая «Легенду»):
Рисунок 1
Новый игрок стартует в рейтинге с 25-го уровня. За выигрыш партии игрок получает «звезду» (иногда – две), т.е. повышает свой подуровень на 1 (или 2 соответственно).
На линейке есть 4 диапазона, в которых отличаются правила изменения уровня игрока при выигрыше\проигрыше партии:
Таблица 1
| Условное наименование | Диапазон уровней | Правила изменения подуровня при победе\поражении |
|---|---|---|
| «Трамплин» | 25-21 | Поражение: подуровень не меняется Победа: +1 3(и более) победы подряд: +2 |
| «Гонка с ускорением» | 20-6 | Поражение: -1 Победа: +1 3(и более) победы подряд: +2 |
| «Нормальная гонка» | 5-1 | Поражение: -1 Победа: +1 |
| «Легенда» | Легенда | Поражение: подуровень не меняется Победа: подуровень не меняется |
Очевидно, что «Трамплин» служит для вовлечения новых игроков, так как на «трамплине» есть только награда, но нет наказания за пора��ение. Кроме того, понятно, что население «трамплина» экспоненциально быстро «вымирает», поскольку правила неизбежно выталкивают игрока с «трамплина» в диапазон «Гонки с ускорением». Вероятность остаться на «трамплине» после 18 игр составляет ~29%, а после 27 игр – менее 1,5%.
«Гонка с ускорением» помогает игрокам с высоким мастерством и хорошими колодами быстрее добраться до «Нормальной гонки», где и начинается настоящее «рубилово». Ну и, наконец, «Легенда» — загончик для топовых игроков.
Мне хотелось найти 2 зависимости:
- Вычислить вероятность получения игроком определённого уровня после определённого количества сыгранных игр;
- Вычислить распределение всех игроков по уровням в зависимости от времени.
Выбор метода решения и инструмента
Первой мыслью было написать программу на JS, моделирующую множество игроков, уровни которых в результате взаимодействия меняются по вышеприведённым правилам. По недолгом размышлении об объёме требуемого JS кода я решил, что электронные таблицы отлично подходят для решения этой задачи.
Идея решения следующая:
Пусть некоторый прямоугольный диапазон размером 96*1 (например диапазон Source!$C$3:$C$98 в прилагаемых файлах) представляет распределение количества игроков по линейке. Тогда, используя правила из таблицы 1, легко получить распределение, описывающее состояние, после того, как каждый игрок сыграл одну игру. Правила из таблицы 1 расположены в диапазоне Source!$D3:$D$98. Если «протащить» эти правила на нужное количество столбцов, то получившая таблица будет представлять изменение распределения игроков по уровням со «временем». Время в данном случае в кавычках потому, что здесь оно измеряется в «сыгранных играх».
Я начал с Open Office Calc, который всем хорош, но 3-D графики «из коробки» в нём выглядят убого (возможно, я просто не умею их готовить). В итоге решение реализовано на MS Excel и лежит здесь. Вариант для Open Office Calc там же — вполне функциональный, за исключением отсутствия 3-D графиков и отсутствия интерактивности в 2-D графиках.
Вероятность получения игроком определённого уровня
Рисунок 2
Приведённые графики описывают вероятность получить тот или иной уровень для игрока, стартовавшего с 25 уровня и сыгравшего 50, 130, 300, 450 или 570 игр соответственно. В Excel график интерактивный – можно поиграться с числами слева от диаграммы на вкладке «Interface», при этом графики (Рисунок 2) будут меняться.
В 3-D эволюция вероятности получения определённого уровня выглядит очень симпатично:
Рисунок 3
Здесь приведён срез с теми же минимальной и максимальной «временными» границами (50 и 570 игр), что и на рисунке 2.
Тот же график с другого ракурса:
Рисунок 4
Несколько неожиданным выглядит появление «ребра» на графиках в точке, соответствующей уровню 5 и 2 «звезды» (72-й подуровень по порядку). Данная точка является последней, на которую действует возможность попадания «с ускорением» после 3+ побед подряд.
Если посмотреть правила для 71 – 72 подуровней, то они выглядят следующим образом:
71 =1/8*C69+C70*3/8+0,5*C72
72 =1/8*C70+C71*1/2+0,5*C73
Здесь СNN- количество игроков на подуровне NN на предыдущем шаге:
— первый член обеспечивает «ускоренный перенос» с уровня «текущий -2»;
— второй член обеспечивает обычный переход при победе на уровне «текущий -1»;
— третий член обеспечивает переход с вышележащего уровня при поражении.
Разница в 1/8 в коэффициенте при втором члене обусловлена тем, что, начиная с 5-го уровня (он же 71-й порядковый подуровень), независимо от числа побед подряд, повышение подуровня проходит только на 1, т.е. даже если победа на 71-м подуровне была для игрока 3-й, он перейдёт лишь на 72-й подуровень.
Эта небольшая на первый взгляд добавка приводит к тому, что «поток игроков» на 72-й подуровень чуть выше среднего, соответственно чуть выше будет и поток игроков с 72-го подуровня в его окрестности, т.е. эффект повышения потока игроков на 72-й подуровень самоусиливается, что и приводит к появлению этого замечательного ребра.
Вычисление распределения всех игроков по уровням
Очевидно, что игроки различаются по количеству игр, которые они играют за одно и то же время. Более увлечённые игроки играют больше, казуальные – меньше.
Для вычисления модельного распределения игроков по уровням необходимо знать функцию распределения игроков по количеству сыгранных ими игр.
Введём обозначения:
- P(L,i) ) — вероятность получения игроком определённо��о уровня (L) после заданного количества игр (i) (графики приведены на рисунках 2-4)
- N – максимальное количество игр, сыгранное самым увлечённым игроком. Заметим, что N здесь играет роль времени. Конечно, это не обычное время. Однако между обычным временем t и N есть следующее соотношение:
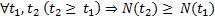, поэтому N в качестве «времени» вполне годится. - Z (i, N) – вероятность того, что игрок сыграл i игр к моменту «времени» N или распределение игроков по количеству сыгранных игр за «время» N.
- D (L,N) – искомая вероятность нахождения игрока на уровне L, в момент «времени» N или распределение игроков по уровням на момент «времени» N.
Тогда
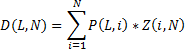
Сразу скажу, что данных о функции Z(i, N) у меня нет. Но можно немного поспекулировать на эту тему.
Единственное, что пришло мне в голову: «20% людей выпивают 80% пива». Возможно, «20% игроков в Hearthstone играют 80% игр»? То есть гипотеза состоит в том, что распределение игроков по количеству сыгранных игр – это дискретное распределение Парето, или, более точно – распределение Ципфа (см. en.wikipedia.org/wiki/Zipf%27s_law).
Введём обозначения:
- Вспомогательная функция
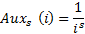
- Нормировочный множитель (для момента «времени» N)
Тогда распределение Ципфа со степенным показателем s:
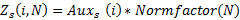
Посмотрим на графики искомой функции D (L,N) в предположении, что распределение игроков по количеству сыгранных игр это распределение Ципфа с показателем степени 1.
Здесь и на следующем графике отображена D (L,N) в моменты «времени» N с 50 до 700.
Рисунок 5
Рисунок 6
Выглядит довольно уродливо, хотя и понятно почему – значительная часть игроков в соответствии с распределением Ципфа осталась на «трамплине». Ну что ж, спекулировать – так по полной. Построим модифицированное распределение Ципфа-Мандельброта (см. en.wikipedia.org/wiki/Zipf%E2%80%93Mandelbrot_law).
1. Заменим вспомогательную функцию
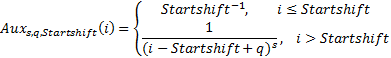
Идея введения целочисленного параметра Startshift состоит в следующем: начало «действия» стандартного поведения распределения Ципфа сдвинуто на Startshift шагов.
Действительно, представляется неправдоподобным, что игрок, прошедший все трудности обучения и только вышедший на рейтинговые игры, с высокой вероятностью бросит играть после одной-двух рейтинговых игр. Можно предположить, что начало «действия» распределения Ципфа примерно совпадает с началом трудностей в продвижении в рейтинге, т.е. с моментом, когда вероятность покинуть «трамплин» превысит ½ (это означает, что startshift=18). Кроме того, из определения вспомогательной функции следует, что общее число игроков «случайно зашедших в Hearthstone» (т.е. сыгравших ≤Startshift игр) совпадает с числом игроков на максимуме распределения. Всё это, конечно, чистая спекуляция, но почему бы не посмотреть, что получится?
Параметр Мандельброта q введён без какого-либо обоснования, на всякий случай.
2. Нормировочный множитель (для момента «времени» N)
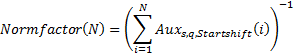
Тогда модифицированное распределение со степенным показателем s, параметром Мандельброта q и параметром «стартового сдвига» Startshift:
Посмотрим, что получается при параметрах, приведённых в нижней части графика:
Рисунок 7
Для ручных экспериментов график в Excel сделан интерактивным – можно поиграться с параметрами распределения и отображаемыми «временами» слева от диаграммы на вкладке «Interface», при этом графики (Рисунок 7 и Рисунок 8) будут меняться.
Рисунок 8
И наконец, последний рывок на сегодня. Попробуем подобрать параметры распределения, используя «реальные» данные (http://www.reddit.com/r/hearthstone/comments/23ed7l/how_good_are_you_at_constructed_ladder/). Это результаты какой-то симуляции, детали которой мне неизвестны, неясно, в частности, в какой момент «времени» N проведено измерение и т.д. Это единственное, что я нашёл. Но я не очень старался искать. Надеюсь, читатели статьи подскажут источник более релевантных данных.
Итерационная обработка данных надстройкой solver и ручная подгонка дали следующие значения параметров распределения: s=1,19; q=0,287; Startshift =110. Startshift ожидаемо большой, поскольку в исходных данных симуляции отсутствует информация о населении уровней 25-21, т.е. «трамплин», очевидно, не симулировался.
Финальные картинки:
Рисунок 9
Рисунок 10
Заключение
В заключение повторюсь, что задача, которую я стал решать из чистого любопытства, показалась мне неплохой темой для занятия в школьном математическом кружке. Считаю важным для будущих инженеров и учёных умение использовать для решения внезапно возникающих задач все имеющиеся подручные инструменты: бумагу и карандаш, электронные таблицы, пакет «WOLFRAM MATHEMATICA». Надеюсь, настоящий пример применения электронной таблицы будет кому-нибудь полезен.
При желании преподаватель может проложить мостики от этой задачи ко множеству тем.
Навскидку:
- Теорвер – распределение Парето – Дзета функция – John Derbyshire. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics
- Численные методы решения дифуров в частных производных. (кстати – задача для продвинутых школьников: покажите, что P(L,i) в диапазоне «Нормальная гонка» аппроксимирует некоторое частное решение уравнения
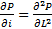в соответствующем масштабе, а в диапазоне «Гонка с ускорением» — уравнения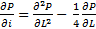 
- Выбор оптимального для задачи вида функции невязки.
Также можно придумать какие-нибудь расширения к данной задаче. Например, такие:
1) Когда заканчивается сезон, то игроки, достигнувшие определённых уровней в прошлом сезоне, получают некоторую фору. Например, при окончании сезона на уровне 4 игрок получает 21 «звезду», т.е. стартует в новом сезоне не с 25 уровня, а с уровня 17.**- он же 21-й порядковый подуровень (см. Рисунок 1). Уверен, что соответствующие цифры, описывающие зависимость размера форы от достигнутого уровня, легко найти в сети.
Вопросы:
- Как изменятся P(L,i) и D (L,N) при учёте форы на старте сезона?
- Сходится ли ряд функций D(L,N, номер сезона) к чему-нибудь при номере сезона, стремящемся к ∞? Если да, то какие ограничения это накладывает на Z (i, N)?
- Достаточно ли Z (i, N) для корректного ответа на 2-й вопрос?
2) Придумать какую-нибудь внятную теорию для вычисления функции Z(i, N).
