Предлагаю читателям «Хабрахабра» перевод поста «Deep Learning, NLP, and Representations» крутого Кристофера Олаха. Иллюстрации оттуда же.
В последние годы методы, использующие глубокое обучение нейросетей (deep neural networks), заняли ведущее положение в распознавании образов. Благодаря им планка для качества методов компьютерного зрения значительно поднялась. В ту же сторону движется и распознавание речи.
Результаты результатами, но почему они так круто решают задачи?
В посте освещено несколько впечатляющих результатов применения глубоких нейронных сетей в обработке естественного языка (Natural Language Processing; NLP). Таким образом я надеюсь доходчиво изложить один из ответов на вопрос, почему глубокие нейросети работают.
Нейросеть со скрытым слоем универсальна: при достаточно большом количестве скрытых узлов она может построить приближение любой функции. Об этом есть часто цитируемая (и ещё чаще неверно понимаемая и применяемая) теорема.
Это верно, поскольку скрытый слой можно просто использовать как «справочную таблицу».
Для простоты рассмотрим перцептрон. Это очень простой нейрон, который срабатывает, если его значение превышает пороговую величину, и не срабатывает, если нет. У перцептрона бинарные входы и бинарный выход (т.е. 0 или 1). Количество вариантов значений на входе ограничено. Каждому из них можно сопоставить нейрон в скрытом слое, который срабатывает только для данного входа.
Разбор «условия» для каждого отдельного входа потребует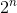
скрытых нейронов (при n данных). На деле обычно всё не так плохо. Могуть быть «условия», под которые подходят несколько входных значений, и могут быть «накладывающиеся друг на друга» «условия», которые достигают правильных входов на своём пересечении.
Затем можем использовать связи между этим нейроном и нейронами на выходе, чтобы задать итоговое значение для этого конкретного случая.
Универсальностью обладают не только перцептроны. Сети с сигмоидами в нейронах (и другими функциями активации) также универсальны: при достаточном количестве скрытых нейронов, они могут построить сколь угодно точное приближение любой непрерывной функции. Продемонстрировать это значительно сложнее, так как нельзя просто так взять и изолировать входы друг от друга.
Поэтому и выходит, что нейронные сети с одним скрытым слоем в самом деле универсальны. Однако в этом нет ничего впечатляющего или удивительного. То, что модель может работать как справочная таблица, — не самый сильный аргумент в пользу нейросетей. Это всего-навсего означает, что модель в принципе способна справиться с задачей. Под универсальностью понимается только то, что сеть может подстроиться под любые выборки, но это вовсе не значит, что она в состоянии адекватно интерполировать решение для работы с новыми данными.
Нет, универсальность ещё не объясняет, почему нейросети так хорошо работают. Правильный ответ лежит несколько глубже. Чтобы разобраться, сначала рассмотрим несколько конкретных результатов.
Начну с особенно интересной подобласти глубокого обучения — с векторных представлений слов (word embeddings). По-моему, сейчас векторные представления — одна из самых крутых тем для исследований в глубоком обучении, хотя впервые они были предложены Bengio, et al. более 10 лет назад.
Векторные представления были впервые предложены в работах Bengio et al, 2001 и Bengio et al, 2003 за несколько лет до воскрешения глубокого обучения в 2006 году, когда нейросети ещё не были в моде. Идея распределённых представлений как таковых ещё старше (см., например, Hinton 1986).
Кроме того, я думаю, что это одна из тех задач, с помощью которых лучше всего формируется интуитивное понимание, почему глубокое обучение так эффективно.
Векторное представление слова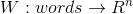
— параметризованная функция, отображающая слова из некоторого естественного языка в векторы большой размерности (допустим, от 200 до 500 измерений). Например, это может выглядеть так:
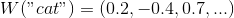
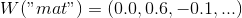
(Как правило, эта функция задаётся таблицей поиска, определяющейся матрицей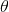
, в которой каждому слову соответствует строка 
).
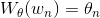W инициализируется случайными векторами для каждого слова. Она будет обучаться, чтобы выдавать осмысленные значения для решения некоторой задачи.
Например, мы можем натаскивать сеть на определение, «корректна» ли 5-грамма (последовательность из пяти слов, например, 'cat sat on the mat'). 5-граммы можно легко получить из Википедии, а затем половину из них «испортить», заменив в каждой какое-нибудь из слов на случайное (например, 'cat sat song the mat'), так как это почти всегда делает 5-грамму бессмысленной.
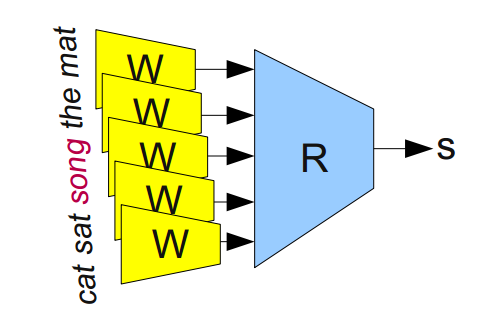
Модульная сеть для определения, «корректна» ли 5-грамма (Bottou (2011)).
Модель, которую мы обучаем, пропустит каждое слово из 5-граммы через W, получив на выходе их векторные представления, и подаст их на вход другому модулю, R, который попытается предсказать, «корректна» 5-грамма или нет. Хотим, чтобы было так:
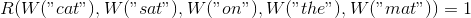
Чтобы предсказывать эти значения точно, сети нужно хорошо подобрать параметры для W и R.
Однако эта задачка скучновата. Вероятно, найденное решение поможет находить в текстах грамматические ошибки или что-то в этом духе. Но что тут по-настоящему ценно, так это полученная W.
(На самом деле, вся соль задания в обучении W. Мы могли бы рассмотреть решения и других задач; так, одно из распространённых — предсказание следующего слова в предложении. Но не это сейчас наша цель. В оставшейся части этого раздела мы поговорим о многих результатах векторного представления слов и не будем отвлекаться на освещение разницы между подходами).
Чтобы «почувствовать», как устроено пространство векторных представлений, можно изобразить их с помощью хитрого метода визуализации данных высокой размерности — tSNE.
Визуализация векторных представлений слов с помощью tSNE. Слева — «область чисел», справа — «область профессий» (из Turian et al. (2010)).
Такая «карта слов» кажется вполне осмысленной. «Похожие» слова близко, и, если посмотреть, какие представления ближе прочих к данному, выходит, что в то же время и близкие «похожи».
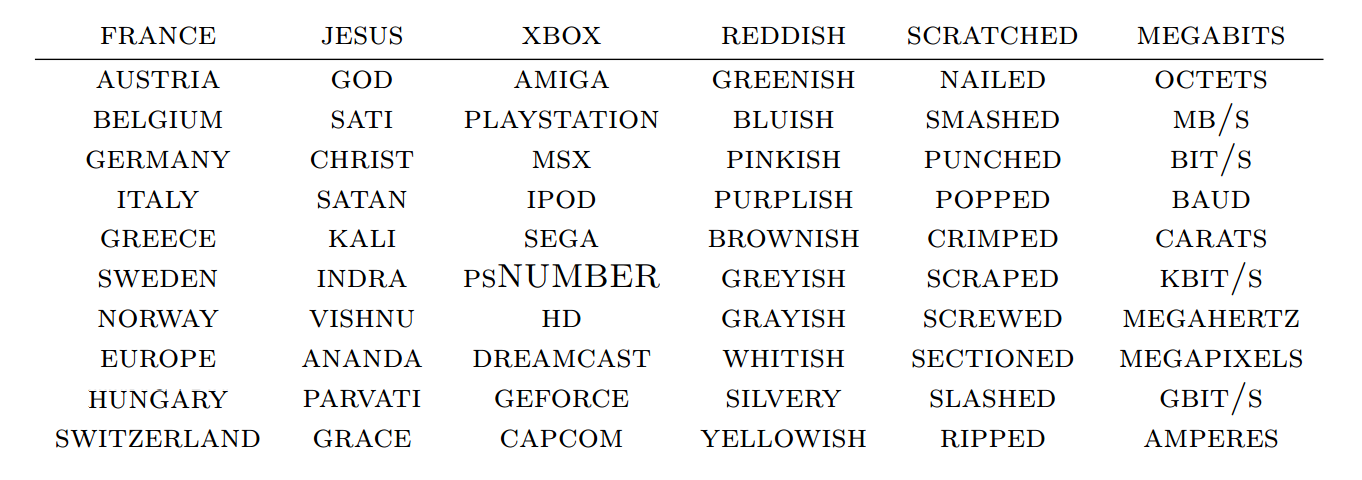
Чьи векторные представления находятся ближе к представлению данного слова? (Collobert et al. (2011).)
Кажется естественным, что сеть сопоставит словам с похожими значениями близкие друг к другу векторы. Если заменить слово на синоним («некоторые хорошо поют»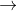
«немногие хорошо поют»), то «корректность» предложения не меняется. Казалось бы, предложения на входе отличаются значительно, но так как W «сдвигает» представления синонимов («некоторые» и «немногие») друг к другу, для R мало что меняется.
Это мощное средство. Число возможных 5-грамм огромно, в то время как размер обучающей выборки сравнительно мал. Сближение представлений похожих слов позволяет нам, взяв одно предложение, как бы работать с целым классом «похожих» на него. Дело не ограничивается заменой синонимов, например, возможна подстановка слова из того же класса («стена голубая»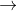 «стена красная»). Более того, есть смысл и в одновременной замене нескольких слов («стена голубая» «потолок красный»). Число таких «похожих фраз» растёт по экспоненте от числа слов.
Уже в основополагающей работе A Neural Probabilistic Language Model (Bengio, et al. 2003) даются содержательные пояснения, почему векторные представления — настолько мощный инструмент.
Очевидно, что это свойство W было бы очень полезным. Но как её обучают? Очень вероятно, что много раз W сталкивается с предложением «стена синяя» и распознаёт его как корректное перед тем, как увидеть предложение «стена красная». Сдвиг «красная» ближе к «синяя» улучшает работу сети.
Нам всё ещё надо иметь дело с примерами употреблений каждого слова, но аналогиии позволяют обобщать на новые комбинации слов. Со всеми словами, значение которых мы понимаем, мы раньше сталкивались, но смысл предложения можно понять, никогда его до этого не слышав. То же умеют и нейронные сети.
Mikolov et al. (2013a)
Векторные представления обладают ещё одним куда более примечательным свойством: похоже, отношения аналогии между словами определяются значением вектора разности между их представлениями. Например, судя по всему, вектор разности «мужских-женских» слов — постоянный:
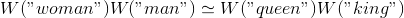
Может, это никого сильно не удивит. В конце концов, наличие местоимений, имеющих род, говорит о том, что замена слова «убивает» грамматическую правильность предложения. Мы пишем: «она — тётя», но «он — дядя». Аналогично, «он — король» и «она — королева». Если мы видим в тексте «она — дядя», скорее всего, это грамматическая ошибка. Если в половине случаев слова заменили случайным образом, то вот, должно быть, наш случай.
«Конечно!» — скажем мы, оглядываясь на прошлый опыт. — «Векторные представления сумеют представить пол. Наверняка есть отдельное измерение для пола. И так же для множественного/единственного числа. Да подобные отношения и так легко распознаются!»
Выясняется, однако, что и куда более сложные отношения «закодированы» аналогично. Просто чудеса в решете (ну, почти)!
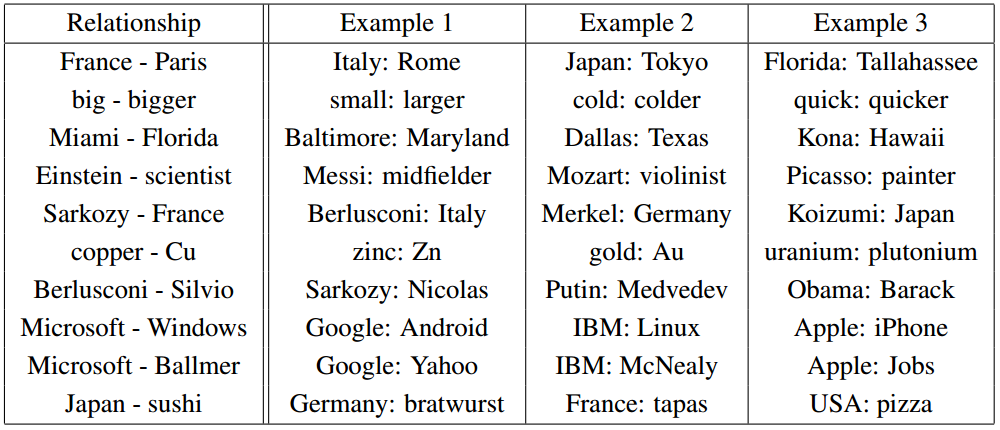
Пары отношений (из Mikolov et al. (2013b).)
Важно, что все эти свойства W — побочные эффекты. Мы не накладывали требований о том, что представления похожих слов должны быть близко друг к у другу. Мы не пытались сами настраивать аналогии с помощью разностей векторов. Мы всего лишь попытались научиться проверять, «корректно» ли предложение, а свойства откуда-то взялись сами собой в процессе решения задачи оптимизации.
Кажется, великая сила нейронных сетей заключается в том, что они автоматически учатся строить «лучшие» представления данных. В свою очередь представление данных — существенная часть решения многих задач машинного обучения. А векторные представления слов — это один из наиболее удивительных примеров обучения представлений (learning a representation).
Свойства векторных представлений, конечно, любопытны, но можем ли мы с их помощью сделать что-то полезное? Кроме глупых мелочей вроде проверки, «корректна» ли та или иная 5-грамма.
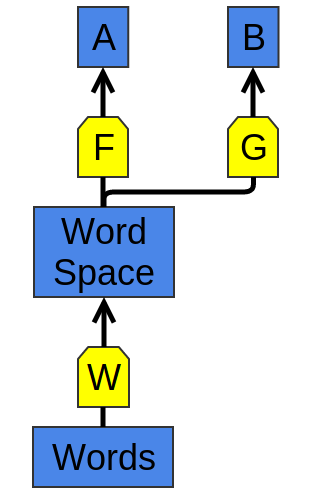
W и F обучают, подгоняя под задачу A. Затем G сможет учиться решать задачу B, используя W.
Мы обучили векторные представления слов, чтобы хорошо справляться с простыми задачками, но, зная их чудные свойства, которые мы уже наблюдали, можно полагать, что они пригодятся и для более общих проблем. В самом деле, векторные представления вроде этих ужасно важны:
(Luong et al. (2013).)
Общая стратегия — обучить хорошее представление для задачи A и использовать его для решения задачи B — один из главных фокусов в волшебной шляпе глубокого обучения. В разных случаях его называют по-разному: предобучение (pretraining), transfer learning, и многоцелевое обучение (multi-task learning). Одна из сильных сторон такого подхода — он позволяет обучать представления на нескольких видах данных.
Можно провернуть эту хитрость по-другому. Вместо настройки представлений для одного типа данных и использования их для решения задач разного вида, можно отображать различные типы данных в единое представление!
Один из замечательных примеров использования такого трюка — векторные представления слов для двух языков, предложенные Socher et al. (2013a). Мы можем научиться «встраивать» слова из двух языков в единое пространство. В данной работе «встраиваются» слова из английского языка и путунхуа («мандаринское наречие» китайского).
Мы обучаем два векторных представления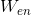
и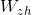 
так же, как делали это выше. Однако нам известно, что некоторые слова в английском и китайском язызках имеют похожие значения. Так, будем оптимизировать и ещё по одному критерию: представления известных нам переводов должны находиться на малом расстоянии друг от друга.
Конечно, в итоге мы наблюдаем, что известные нам «похожие» слова укладываются рядом. Неудивительно, ведь мы так оптимизировали. Куда интереснее вот что: переводы, о которых мы не знали, тоже оказываются рядом.
Возможно, это никого уже не удивляет в свете нашего прошлого опыта с векторными представлениями слов. Они «притягивают» похожие слова друг к другу, поэтому, если мы знаем, что английское и китайское слова значат примерно одно и то же, то и представления их синонимов должны находиться поблизости. Нам также известно, что пары слов в отношениях вроде различия родов (полов) отличаются на постоянный вектор. Похоже, если «стягивать» достаточное количество переводов, то удастся подогнать и разности так, чтобы они были одинаковыми в двух языках. В результате, если «мужские версии» слова в обоих языках переводятся друг в друга, автоматически получим, что и «женские версии» тоже правильно переводятся.
Интуиция подсказывает, что, должно быть, языки имеют похожую «структуру» и что, насильно связывая их в выделенных точках, мы подтягиваем и остальные представления на нужные места.
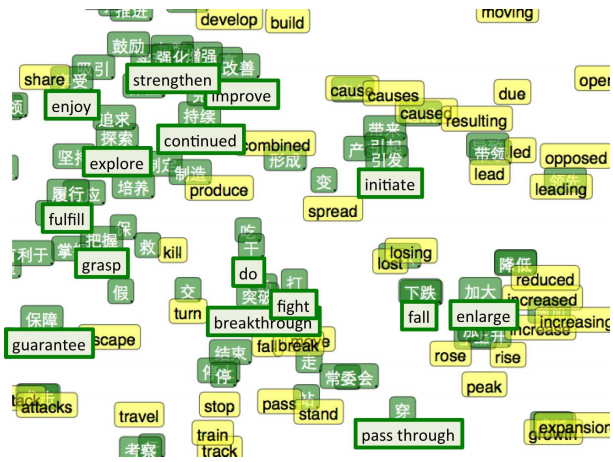
Визулизация двуязычных векторных представлений с помощью t-SNE. Зелёным цветом отмечен китайский, Жёлтым — английский (Socher et al. (2013a)).
Когда имеем дело с двумя языками, мы обучаем единое для двух похожих типов данных представление. Но можем «вписывать» в единое пространство и сильно отличающиеся виды данных.
Недавно с помощью глубокого обучения стали строить модели, которые «вписывают» изображения и слова в единое пространство представлений
В предыдущей работе моделировали совместное распределение меток и изображений, но здесь всё немного иначе.
Основная идея в том, что мы классифицируем изображения, выдавая вектор из пространства представлений слов. Картинки с собаками отображаются в векторы около представления слова «собака», с лошадьми — около «лошадь», с авто — около «автомобиль». И так далее.
Самое интересное происходит, когда вы проверяете модель на новых классах изображений. Так, что будет, если предложить классифицировать изображение котика модели, которую не учили специально их распознавать, то есть отображать в вектор, близкий к вектору «кошка»?
Socher et al. (2013b)
Оказывается, сеть неплохо справляется с новыми классами изображений. Изображения котов не отображаются в случайные точки в пространстве. Напротив, они укладываются в окрестности вектора «пёс» и довольно близко к вектору «кот». Аналогично, изображения грузовиков отображаются в точки, близкие к вектору «грузовик», который находится недалеко от связанного вектора «автомобиль».
Socher et al. (2013b)
Участники стэнфордской группы проделали это с 8 известными классами и двумя неизвестными. Результаты уже впечатляют. Но при таком небольшом числе классов маловато точек, по которым можно интерполировать отношение между изображениями и семантическим пространством.
Исследовательская группа Google построила куда более масштабную версию того же; они взяли 1000 категорий вместо 8 — и примерно в то же время (Frome et al. (2013)), а затем предложили ещё один вариант (Norouzi et al. (2014)). Две последних работы основаны на сильной модели классификации изображений (Krizehvsky et al. (2012)), но изображения в них укладываются в пространство векторных представлений слов по-разному.
И результаты впечатляют. Если и не удаётся точно сопоставить изображениям неизвестных классов правильный вектор, то по крайней мере удаётся попасть в верную окрестность. Поэтому, если пытаться классифицировать изображения из неизвестных и значительно отличающихся друг от друга категорий, то классы по крайней мере можно различать.
Даже если я никогда не видел ни эскулапова полоза, ни броненосца, когда мне покажут их снимки, я смогу сказать, кто где изображён, потому что у меня есть общее представление, какой внешний вид могут иметь этот животные. И такие сети тоже на это способны.
(Мы часто использовали фразу «эти слова похожи». Но кажется, что можно получить куда более сильные результаты, основанные на отношениях между словами. В нашем пространстве представлений слов сохраняется постоянная разность между «мужскими» и «женскими версиями». Но и в пространстве представлений изображений есть воспроизводимые свойства, позволяющие увидеть разницу между полами. Борода, усы и лысая голова — хорошо распознаваемые признаки мужчины. Грудь и длинные волосы (менее надёжный признак), макияж и украшения — очевидные индикаторы женского пола Я прекрасно понимаю, что физические признаки пола обманчивы. Так, например, я не стану утверждать, что все лысые — мужчины или что все, у кого есть бюст, — женщины. Но то, что это чаще верно, чем нет, поможет нам лучше задать начальные значения.
. Даже если вы никогда не видели короля, то, увидев королеву (которую вы опознали по короне) с бородой, вы наверняка решите, что надо использовать «мужскую версию» слова «королева»).
Общие представления (shared embeddings) — захватывающая дух область исследований; они — очень убедительный аргумент в пользу того, чтобы на фронтах глубокого обучения продвигать именно обучение представлений.
Мы начали обсуждение векторных представлений слов с такой сети:
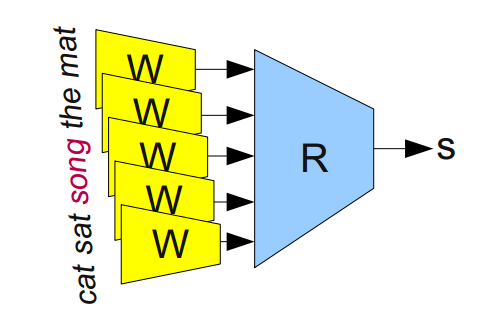
Модульная сеть (Modular Network), обучающая векторные представления слов (Bottou (2011)).
На схеме изображена модульная сеть
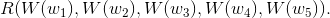
Она построена из двух модулей, W и R. Такой подход к построению нейросетей — из меньших «нейросетевых модулей» — не слишком широко распространён. Однако он очень хорошо показал себя в задачах обработки естественного языка.
Модели, о которых было рассказывано, сильны, но у них есть одно досадное ограничение: число входов у них не может меняться.
С этим можно справиться, добавив ассоциирующий модуль A, который «сливает» два векторных представления.
Из Bottou (2011)
«Сливая» последовательности слов, A позволяет представлять фразы и даже целые предложения. И так как мы хотим «сливать» разное количество слов, число входов не должно быть ограниченным.
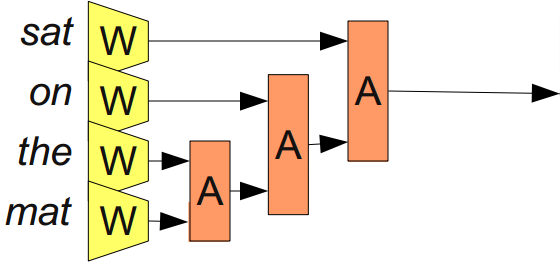
Не факт, что правильно «сливать» слова в предложении просто по порядку. Предложение 'the cat sat on the mat' можно разобрать на части так: '((the cat) (sat (on (the mat))'. Можем применить A, используя такую расстановку скобок:
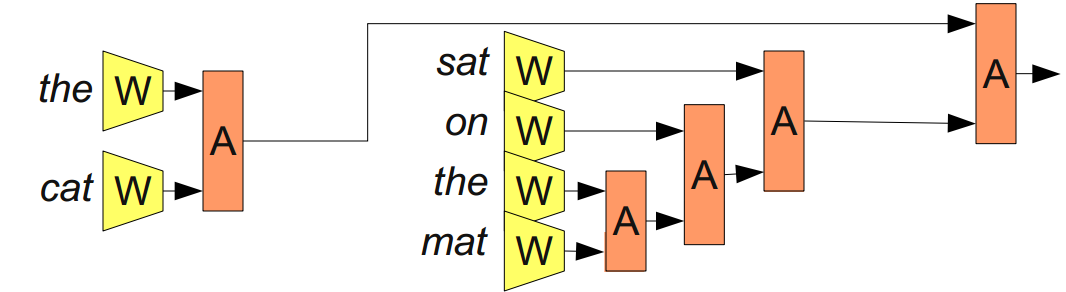
Из Bottou (2011)
Эти модели часто называют рекурсивными нейронными сетями (recursive neural networks), так как выходной сигнал одного модуля часто подаётся на вход другому модулю того же типа. Иногда их ещё называют нейронными сетями древовидной структуры (tree-structured neural networks).
Рекурсивные нейронные сети добились значительного успеха в решении нескольких задач обработки естественного языка. Например, в Socher et al. (2013c) они используются для предсказания тональности предложения:
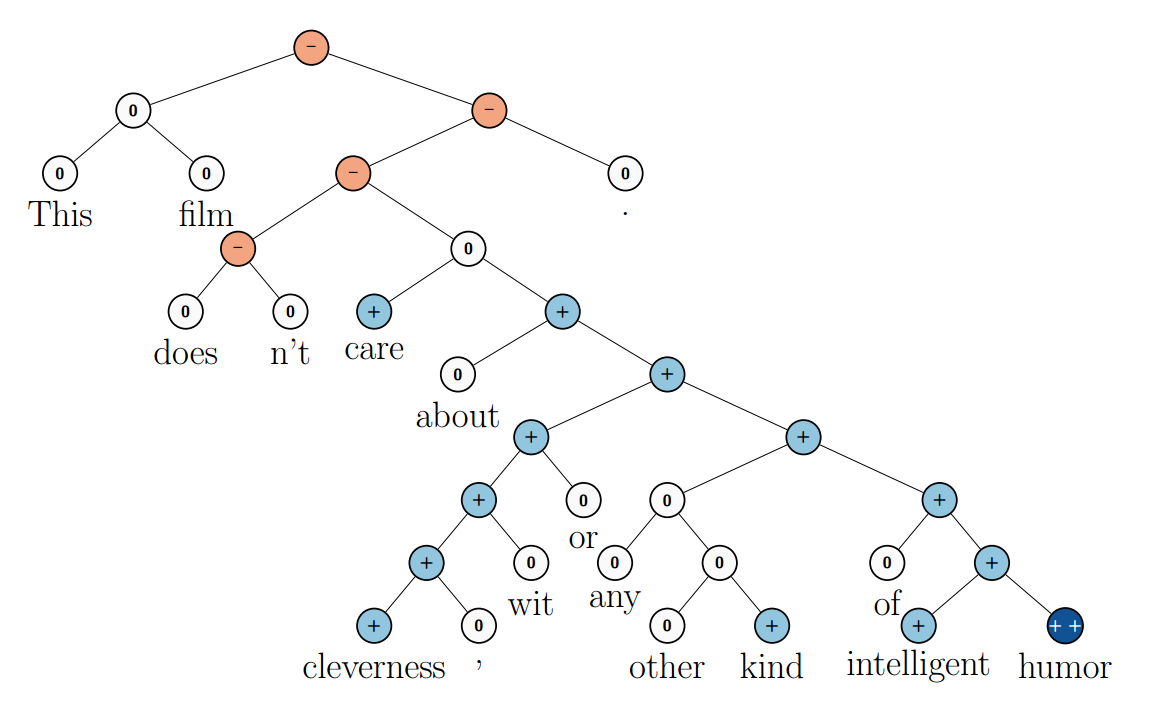
(Из Socher et al. (2013c).)
Главная цель — создать «обратимое» представление предложения, то есть такое, что по нему можно восстановить предложение с приблизительно таким же значением. Например, можно попытаться ввести диссоциирующий модуль D, который будет выполнять действие, обратное A:
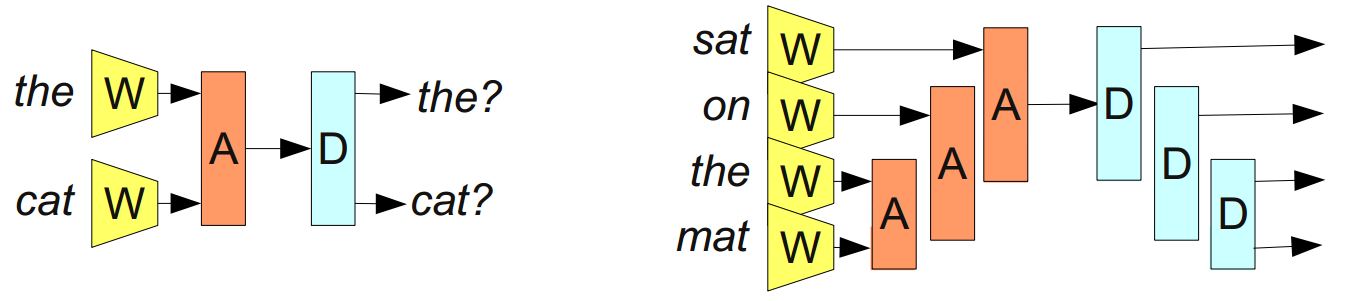
Из Bottou (2011)
Если это удастся, то у нас на руках будет невероятно мощный инструмент. Например, можно будет попытаться построить представления предложений для двух языков и использовать его для автоматического перевода.
К сожалению, оказывается, это очень сложно. Ужасно сложно. Но, получив основания для надежд, над решением задачи бьются многие.
Недавно Cho et al. (2014) был сделан прогресс в представлении фраз, с моделью, которая «кодирует» фразу на английском и «декодирует» её как фразу на французском. Только посмотрите, какие выходят представления!
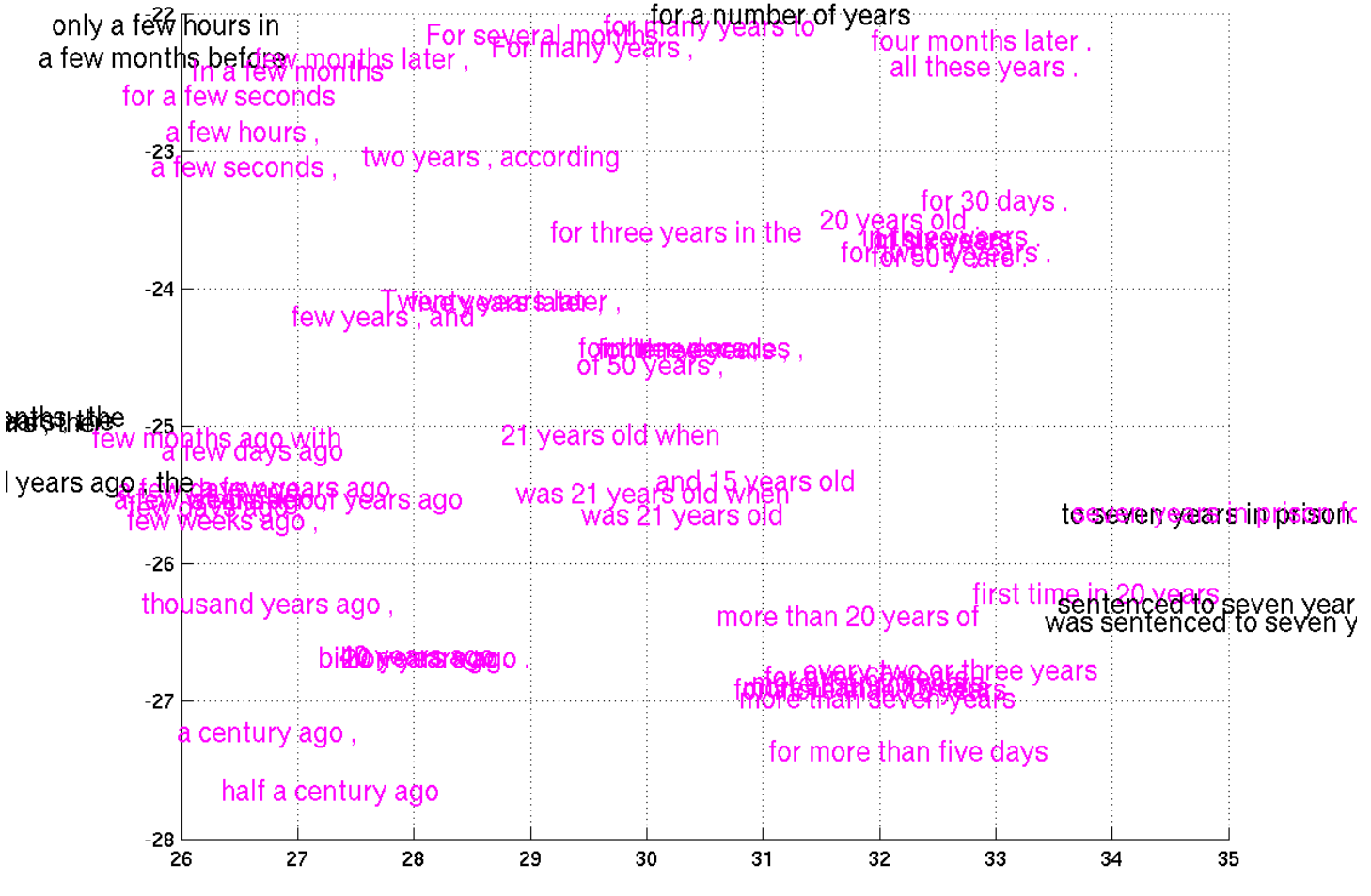
Небольшой кусок пространства представлений, сжатых с помощью tSNE (Cho et al. (2014).)
Я слышал, что некоторые из рассмотренных выше результатов критиковались исследователями из других областей, в частности, лингвистами и специалистами по обработке естественного языка. Критикуются не сами результаты, а следствия, которые из них выводятся, и методы сравнения с другими подходами.
Я не считаю, что подготовлен настолько хорошо, чтобы чётко сформулировать, в чём именно проблема. Был бы рад, если бы кто-нибудь это сделал в комментариях.
Глубокое обучения на службе у обучения представлений — мощный подход, который, кажется, даёт ответ на вопрос, почему нейронные сети так эффективны. Кроме того, есть в нём удивительная красота: почему нейронные сети эффективны? Да потому, что лучшие способы представления данных появляются сами собой в ходе оптимизации многослойных моделей.
Глубокое обучение — очень молодая область, где ещё не устаканились теории и где взгляды быстро меняются. С этой оговоркой скажу, что, как мне кажется, обучение представлений с помощью нейронных сетей сейчас очень популярно.
В этом посте рассказано о многих результатах исследований, которые мне кажутся впечатляющими, но моя основная цель — подготовить почву для следующего поста, в котором будут рассмотрены связи между глубоким обучением, теорией типов и функциональным программированием. Если интересно, то, чтобы его не пропустить, можете подписаться на мой RSS-канал.
Далее автор просит сообщать о замеченных неточностях в комментариях, см. оригинальную статью.
Спасибо Eliana Lorch, Yoshua Bengio, Michael Nielsen, Laura Ball, Rob Gilson и Jacob Steinhardt за комментарии и поддержку.
От переводчика: благодарю за ценные замечания Дениса Кирьянова и Вадима Лебедева.
В последние годы методы, использующие глубокое обучение нейросетей (deep neural networks), заняли ведущее положение в распознавании образов. Благодаря им планка для качества методов компьютерного зрения значительно поднялась. В ту же сторону движется и распознавание речи.
Результаты результатами, но почему они так круто решают задачи?
В посте освещено несколько впечатляющих результатов применения глубоких нейронных сетей в обработке естественного языка (Natural Language Processing; NLP). Таким образом я надеюсь доходчиво изложить один из ответов на вопрос, почему глубокие нейросети работают.
Нейронные сети с одним скрытым слоем
Нейросеть со скрытым слоем универсальна: при достаточно большом количестве скрытых узлов она может построить приближение любой функции. Об этом есть часто цитируемая (и ещё чаще неверно понимаемая и применяемая) теорема.
Это верно, поскольку скрытый слой можно просто использовать как «справочную таблицу».
Для простоты рассмотрим перцептрон. Это очень простой нейрон, который срабатывает, если его значение превышает пороговую величину, и не срабатывает, если нет. У перцептрона бинарные входы и бинарный выход (т.е. 0 или 1). Количество вариантов значений на входе ограничено. Каждому из них можно сопоставить нейрон в скрытом слое, который срабатывает только для данного входа.
Разбор «условия» для каждого отдельного входа потребует
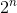скрытых нейронов (при n данных). На деле обычно всё не так плохо. Могуть быть «условия», под которые подходят несколько входных значений, и могут быть «накладывающиеся друг на друга» «условия», которые достигают правильных входов на своём пересечении.Затем можем использовать связи между этим нейроном и нейронами на выходе, чтобы задать итоговое значение для этого конкретного случая.
Универсальностью обладают не только перцептроны. Сети с сигмоидами в нейронах (и другими функциями активации) также универсальны: при достаточном количестве скрытых нейронов, они могут построить сколь угодно точное приближение любой непрерывной функции. Продемонстрировать это значительно сложнее, так как нельзя просто так взять и изолировать входы друг от друга.
Поэтому и выходит, что нейронные сети с одним скрытым слоем в самом деле универсальны. Однако в этом нет ничего впечатляющего или удивительного. То, что модель может работать как справочная таблица, — не самый сильный аргумент в пользу нейросетей. Это всего-навсего означает, что модель в принципе способна справиться с задачей. Под универсальностью понимается только то, что сеть может подстроиться под любые выборки, но это вовсе не значит, что она в состоянии адекватно интерполировать решение для работы с новыми данными.
Нет, универсальность ещё не объясняет, почему нейросети так хорошо работают. Правильный ответ лежит несколько глубже. Чтобы разобраться, сначала рассмотрим несколько конкретных результатов.
Векторные представления слов (word embeddings)
Начну с особенно интересной подобласти глубокого обучения — с векторных представлений слов (word embeddings). По-моему, сейчас векторные представления — одна из самых крутых тем для исследований в глубоком обучении, хотя впервые они были предложены Bengio, et al. более 10 лет назад.
Векторные представления были впервые предложены в работах Bengio et al, 2001 и Bengio et al, 2003 за несколько лет до воскрешения глубокого обучения в 2006 году, когда нейросети ещё не были в моде. Идея распределённых представлений как таковых ещё старше (см., например, Hinton 1986).
Кроме того, я думаю, что это одна из тех задач, с помощью которых лучше всего формируется интуитивное понимание, почему глубокое обучение так эффективно.
Векторное представление слова
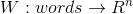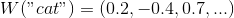
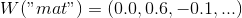
— параметризованная функция, отображающая слова из некоторого естественного языка в векторы большой размерности (допустим, от 200 до 500 измерений). Например, это может выглядеть так:(Как правило, эта функция задаётся таблицей поиска, определяющейся матрицей
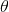, в которой каждому слову соответствует строка 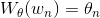).W инициализируется случайными векторами для каждого слова. Она будет обучаться, чтобы выдавать осмысленные значения для решения некоторой задачи.
Например, мы можем натаскивать сеть на определение, «корректна» ли 5-грамма (последовательность из пяти слов, например, 'cat sat on the mat'). 5-граммы можно легко получить из Википедии, а затем половину из них «испортить», заменив в каждой какое-нибудь из слов на случайное (например, 'cat sat song the mat'), так как это почти всегда делает 5-грамму бессмысленной.
Модульная сеть для определения, «корректна» ли 5-грамма (Bottou (2011)).
Модель, которую мы обучаем, пропустит каждое слово из 5-граммы через W, получив на выходе их векторные представления, и подаст их на вход другому модулю, R, который попытается предсказать, «корректна» 5-грамма или нет. Хотим, чтобы было так:
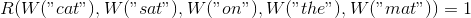
Чтобы предсказывать эти значения точно, сети нужно хорошо подобрать параметры для W и R.
Однако эта задачка скучновата. Вероятно, найденное решение поможет находить в текстах грамматические ошибки или что-то в этом духе. Но что тут по-настоящему ценно, так это полученная W.
(На самом деле, вся соль задания в обучении W. Мы могли бы рассмотреть решения и других задач; так, одно из распространённых — предсказание следующего слова в предложении. Но не это сейчас наша цель. В оставшейся части этого раздела мы поговорим о многих результатах векторного представления слов и не будем отвлекаться на освещение разницы между подходами).
Чтобы «почувствовать», как устроено пространство векторных представлений, можно изобразить их с помощью хитрого метода визуализации данных высокой размерности — tSNE.
Визуализация векторных представлений слов с помощью tSNE. Слева — «область чисел», справа — «область профессий» (из Turian et al. (2010)).
Такая «карта слов» кажется вполне осмысленной. «Похожие» слова близко, и, если посмотреть, какие представления ближе прочих к данному, выходит, что в то же время и близкие «похожи».
Чьи векторные представления находятся ближе к представлению данного слова? (Collobert et al. (2011).)
Кажется естественным, что сеть сопоставит словам с похожими значениями близкие друг к другу векторы. Если заменить слово на синоним («некоторые хорошо поют»
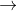«немногие хорошо поют»), то «корректность» предложения не меняется. Казалось бы, предложения на входе отличаются значительно, но так как W «сдвигает» представления синонимов («некоторые» и «немногие») друг к другу, для R мало что меняется.Это мощное средство. Число возможных 5-грамм огромно, в то время как размер обучающей выборки сравнительно мал. Сближение представлений похожих слов позволяет нам, взяв одно предложение, как бы работать с целым классом «похожих» на него. Дело не ограничивается заменой синонимов, например, возможна подстановка слова из того же класса («стена голубая»
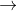«стена красная»). Более того, есть смысл и в одновременной замене нескольких слов («стена голубая» «потолок красный»). Число таких «похожих фраз» растёт по экспоненте от числа слов. Уже в основополагающей работе A Neural Probabilistic Language Model (Bengio, et al. 2003) даются содержательные пояснения, почему векторные представления — настолько мощный инструмент.
Очевидно, что это свойство W было бы очень полезным. Но как её обучают? Очень вероятно, что много раз W сталкивается с предложением «стена синяя» и распознаёт его как корректное перед тем, как увидеть предложение «стена красная». Сдвиг «красная» ближе к «синяя» улучшает работу сети.
Нам всё ещё надо иметь дело с примерами употреблений каждого слова, но аналогиии позволяют обобщать на новые комбинации слов. Со всеми словами, значение которых мы понимаем, мы раньше сталкивались, но смысл предложения можно понять, никогда его до этого не слышав. То же умеют и нейронные сети.
Mikolov et al. (2013a)
Векторные представления обладают ещё одним куда более примечательным свойством: похоже, отношения аналогии между словами определяются значением вектора разности между их представлениями. Например, судя по всему, вектор разности «мужских-женских» слов — постоянный:
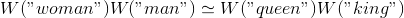
Может, это никого сильно не удивит. В конце концов, наличие местоимений, имеющих род, говорит о том, что замена слова «убивает» грамматическую правильность предложения. Мы пишем: «она — тётя», но «он — дядя». Аналогично, «он — король» и «она — королева». Если мы видим в тексте «она — дядя», скорее всего, это грамматическая ошибка. Если в половине случаев слова заменили случайным образом, то вот, должно быть, наш случай.
«Конечно!» — скажем мы, оглядываясь на прошлый опыт. — «Векторные представления сумеют представить пол. Наверняка есть отдельное измерение для пола. И так же для множественного/единственного числа. Да подобные отношения и так легко распознаются!»
Выясняется, однако, что и куда более сложные отношения «закодированы» аналогично. Просто чудеса в решете (ну, почти)!
Пары отношений (из Mikolov et al. (2013b).)
Важно, что все эти свойства W — побочные эффекты. Мы не накладывали требований о том, что представления похожих слов должны быть близко друг к у другу. Мы не пытались сами настраивать аналогии с помощью разностей векторов. Мы всего лишь попытались научиться проверять, «корректно» ли предложение, а свойства откуда-то взялись сами собой в процессе решения задачи оптимизации.
Кажется, великая сила нейронных сетей заключается в том, что они автоматически учатся строить «лучшие» представления данных. В свою очередь представление данных — существенная часть решения многих задач машинного обучения. А векторные представления слов — это один из наиболее удивительных примеров обучения представлений (learning a representation).
Общие представления (shared representations)
Свойства векторных представлений, конечно, любопытны, но можем ли мы с их помощью сделать что-то полезное? Кроме глупых мелочей вроде проверки, «корректна» ли та или иная 5-грамма.
W и F обучают, подгоняя под задачу A. Затем G сможет учиться решать задачу B, используя W.
Мы обучили векторные представления слов, чтобы хорошо справляться с простыми задачками, но, зная их чудные свойства, которые мы уже наблюдали, можно полагать, что они пригодятся и для более общих проблем. В самом деле, векторные представления вроде этих ужасно важны:
«Использование векторных представлений слов… в последнее время стало главным «секретом фирмы» во многих системах обработки естественного языка, решающих в том числе задачи выделения именованных сущностей (named entity recognition), частеречной разметки (part-of-speech tagging), синтаксического анализа и определения семантических ролей (semantic role labeling)».
(Luong et al. (2013).)
Общая стратегия — обучить хорошее представление для задачи A и использовать его для решения задачи B — один из главных фокусов в волшебной шляпе глубокого обучения. В разных случаях его называют по-разному: предобучение (pretraining), transfer learning, и многоцелевое обучение (multi-task learning). Одна из сильных сторон такого подхода — он позволяет обучать представления на нескольких видах данных.
Можно провернуть эту хитрость по-другому. Вместо настройки представлений для одного типа данных и использования их для решения задач разного вида, можно отображать различные типы данных в единое представление!
Один из замечательных примеров использования такого трюка — векторные представления слов для двух языков, предложенные Socher et al. (2013a). Мы можем научиться «встраивать» слова из двух языков в единое пространство. В данной работе «встраиваются» слова из английского языка и путунхуа («мандаринское наречие» китайского).
Мы обучаем два векторных представления
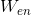и 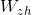так же, как делали это выше. Однако нам известно, что некоторые слова в английском и китайском язызках имеют похожие значения. Так, будем оптимизировать и ещё по одному критерию: представления известных нам переводов должны находиться на малом расстоянии друг от друга.Конечно, в итоге мы наблюдаем, что известные нам «похожие» слова укладываются рядом. Неудивительно, ведь мы так оптимизировали. Куда интереснее вот что: переводы, о которых мы не знали, тоже оказываются рядом.
Возможно, это никого уже не удивляет в свете нашего прошлого опыта с векторными представлениями слов. Они «притягивают» похожие слова друг к другу, поэтому, если мы знаем, что английское и китайское слова значат примерно одно и то же, то и представления их синонимов должны находиться поблизости. Нам также известно, что пары слов в отношениях вроде различия родов (полов) отличаются на постоянный вектор. Похоже, если «стягивать» достаточное количество переводов, то удастся подогнать и разности так, чтобы они были одинаковыми в двух языках. В результате, если «мужские версии» слова в обоих языках переводятся друг в друга, автоматически получим, что и «женские версии» тоже правильно переводятся.
Интуиция подсказывает, что, должно быть, языки имеют похожую «структуру» и что, насильно связывая их в выделенных точках, мы подтягиваем и остальные представления на нужные места.
Визулизация двуязычных векторных представлений с помощью t-SNE. Зелёным цветом отмечен китайский, Жёлтым — английский (Socher et al. (2013a)).
Когда имеем дело с двумя языками, мы обучаем единое для двух похожих типов данных представление. Но можем «вписывать» в единое пространство и сильно отличающиеся виды данных.
Недавно с помощью глубокого обучения стали строить модели, которые «вписывают» изображения и слова в единое пространство представлений
В предыдущей работе моделировали совместное распределение меток и изображений, но здесь всё немного иначе.
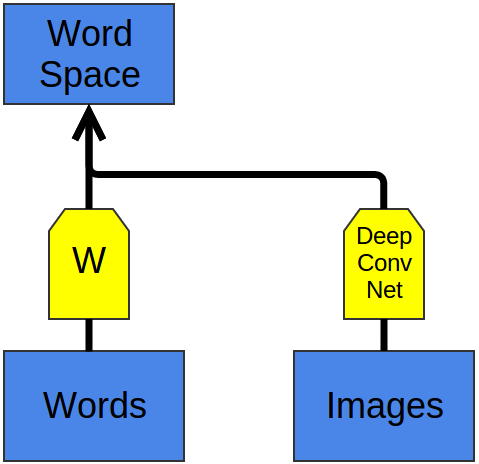
Основная идея в том, что мы классифицируем изображения, выдавая вектор из пространства представлений слов. Картинки с собаками отображаются в векторы около представления слова «собака», с лошадьми — около «лошадь», с авто — около «автомобиль». И так далее.
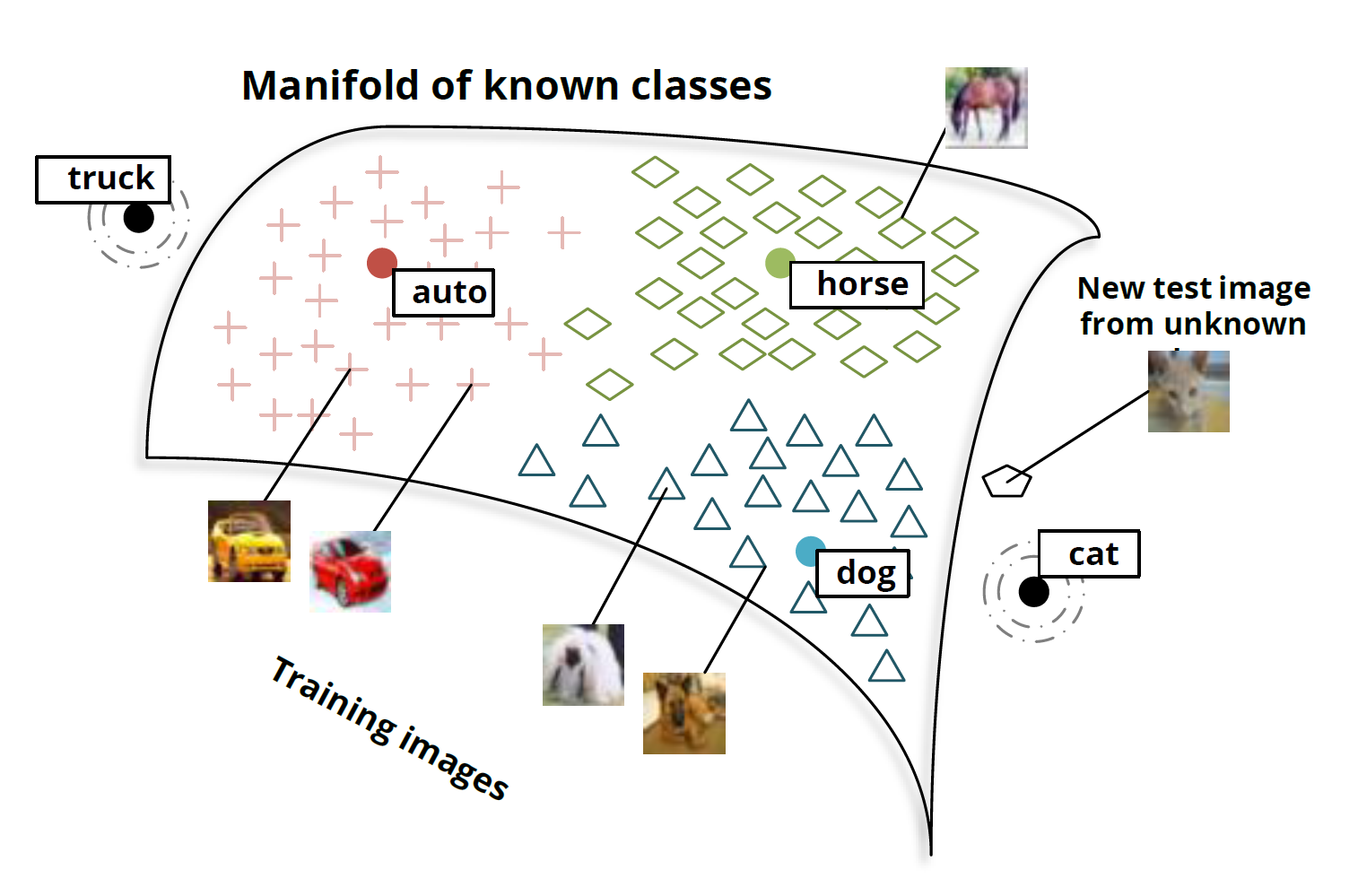
Самое интересное происходит, когда вы проверяете модель на новых классах изображений. Так, что будет, если предложить классифицировать изображение котика модели, которую не учили специально их распознавать, то есть отображать в вектор, близкий к вектору «кошка»?
Socher et al. (2013b)
Оказывается, сеть неплохо справляется с новыми классами изображений. Изображения котов не отображаются в случайные точки в пространстве. Напротив, они укладываются в окрестности вектора «пёс» и довольно близко к вектору «кот». Аналогично, изображения грузовиков отображаются в точки, близкие к вектору «грузовик», который находится недалеко от связанного вектора «автомобиль».
Socher et al. (2013b)
Участники стэнфордской группы проделали это с 8 известными классами и двумя неизвестными. Результаты уже впечатляют. Но при таком небольшом числе классов маловато точек, по которым можно интерполировать отношение между изображениями и семантическим пространством.
Исследовательская группа Google построила куда более масштабную версию того же; они взяли 1000 категорий вместо 8 — и примерно в то же время (Frome et al. (2013)), а затем предложили ещё один вариант (Norouzi et al. (2014)). Две последних работы основаны на сильной модели классификации изображений (Krizehvsky et al. (2012)), но изображения в них укладываются в пространство векторных представлений слов по-разному.
И результаты впечатляют. Если и не удаётся точно сопоставить изображениям неизвестных классов правильный вектор, то по крайней мере удаётся попасть в верную окрестность. Поэтому, если пытаться классифицировать изображения из неизвестных и значительно отличающихся друг от друга категорий, то классы по крайней мере можно различать.
Даже если я никогда не видел ни эскулапова полоза, ни броненосца, когда мне покажут их снимки, я смогу сказать, кто где изображён, потому что у меня есть общее представление, какой внешний вид могут иметь этот животные. И такие сети тоже на это способны.
(Мы часто использовали фразу «эти слова похожи». Но кажется, что можно получить куда более сильные результаты, основанные на отношениях между словами. В нашем пространстве представлений слов сохраняется постоянная разность между «мужскими» и «женскими версиями». Но и в пространстве представлений изображений есть воспроизводимые свойства, позволяющие увидеть разницу между полами. Борода, усы и лысая голова — хорошо распознаваемые признаки мужчины. Грудь и длинные волосы (менее надёжный признак), макияж и украшения — очевидные индикаторы женского пола Я прекрасно понимаю, что физические признаки пола обманчивы. Так, например, я не стану утверждать, что все лысые — мужчины или что все, у кого есть бюст, — женщины. Но то, что это чаще верно, чем нет, поможет нам лучше задать начальные значения.
. Даже если вы никогда не видели короля, то, увидев королеву (которую вы опознали по короне) с бородой, вы наверняка решите, что надо использовать «мужскую версию» слова «королева»).
Общие представления (shared embeddings) — захватывающая дух область исследований; они — очень убедительный аргумент в пользу того, чтобы на фронтах глубокого обучения продвигать именно обучение представлений.
Рекурсивные нейронные сети
Мы начали обсуждение векторных представлений слов с такой сети:
Модульная сеть (Modular Network), обучающая векторные представления слов (Bottou (2011)).
На схеме изображена модульная сеть
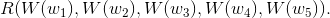
Она построена из двух модулей, W и R. Такой подход к построению нейросетей — из меньших «нейросетевых модулей» — не слишком широко распространён. Однако он очень хорошо показал себя в задачах обработки естественного языка.
Модели, о которых было рассказывано, сильны, но у них есть одно досадное ограничение: число входов у них не может меняться.
С этим можно справиться, добавив ассоциирующий модуль A, который «сливает» два векторных представления.
Из Bottou (2011)
«Сливая» последовательности слов, A позволяет представлять фразы и даже целые предложения. И так как мы хотим «сливать» разное количество слов, число входов не должно быть ограниченным.
Не факт, что правильно «сливать» слова в предложении просто по порядку. Предложение 'the cat sat on the mat' можно разобрать на части так: '((the cat) (sat (on (the mat))'. Можем применить A, используя такую расстановку скобок:
Из Bottou (2011)
Эти модели часто называют рекурсивными нейронными сетями (recursive neural networks), так как выходной сигнал одного модуля часто подаётся на вход другому модулю того же типа. Иногда их ещё называют нейронными сетями древовидной структуры (tree-structured neural networks).
Рекурсивные нейронные сети добились значительного успеха в решении нескольких задач обработки естественного языка. Например, в Socher et al. (2013c) они используются для предсказания тональности предложения:
(Из Socher et al. (2013c).)
Главная цель — создать «обратимое» представление предложения, то есть такое, что по нему можно восстановить предложение с приблизительно таким же значением. Например, можно попытаться ввести диссоциирующий модуль D, который будет выполнять действие, обратное A:
Из Bottou (2011)
Если это удастся, то у нас на руках будет невероятно мощный инструмент. Например, можно будет попытаться построить представления предложений для двух языков и использовать его для автоматического перевода.
К сожалению, оказывается, это очень сложно. Ужасно сложно. Но, получив основания для надежд, над решением задачи бьются многие.
Недавно Cho et al. (2014) был сделан прогресс в представлении фраз, с моделью, которая «кодирует» фразу на английском и «декодирует» её как фразу на французском. Только посмотрите, какие выходят представления!
Небольшой кусок пространства представлений, сжатых с помощью tSNE (Cho et al. (2014).)
Критика
Я слышал, что некоторые из рассмотренных выше результатов критиковались исследователями из других областей, в частности, лингвистами и специалистами по обработке естественного языка. Критикуются не сами результаты, а следствия, которые из них выводятся, и методы сравнения с другими подходами.
Я не считаю, что подготовлен настолько хорошо, чтобы чётко сформулировать, в чём именно проблема. Был бы рад, если бы кто-нибудь это сделал в комментариях.
Заключение
Глубокое обучения на службе у обучения представлений — мощный подход, который, кажется, даёт ответ на вопрос, почему нейронные сети так эффективны. Кроме того, есть в нём удивительная красота: почему нейронные сети эффективны? Да потому, что лучшие способы представления данных появляются сами собой в ходе оптимизации многослойных моделей.
Глубокое обучение — очень молодая область, где ещё не устаканились теории и где взгляды быстро меняются. С этой оговоркой скажу, что, как мне кажется, обучение представлений с помощью нейронных сетей сейчас очень популярно.
В этом посте рассказано о многих результатах исследований, которые мне кажутся впечатляющими, но моя основная цель — подготовить почву для следующего поста, в котором будут рассмотрены связи между глубоким обучением, теорией типов и функциональным программированием. Если интересно, то, чтобы его не пропустить, можете подписаться на мой RSS-канал.
Далее автор просит сообщать о замеченных неточностях в комментариях, см. оригинальную статью.
Благодарности
Спасибо Eliana Lorch, Yoshua Bengio, Michael Nielsen, Laura Ball, Rob Gilson и Jacob Steinhardt за комментарии и поддержку.
От переводчика: благодарю за ценные замечания Дениса Кирьянова и Вадима Лебедева.
