Общие сведения
В статье рассмотрен один из возможных алгоритмов программной реализации парсера арифметических выражений, с возможностью последующего расчета их значений.
Парсер — это программа, анализирующая входное арифметическое выражение. Программы подобного класса, иногда называют так же «распознавателями».
Парсинг — процесс разбора входного арифметического выражения на более простые составляющие.
Результатом работы парсера является сформированное дерево лексем. Под лексемами будем понимать фрагменты входного арифметического выражения, которые не подлежат дальнейшему разбиению на составные части.
Описание алгоритма распознавания приводится без привязки к какому-либо языку программирования. В заключении статьи приведен пример реализации данного алгоритма на PHP. Возможна реализация алгоритма практически на любом языке программирования (даже без поддержки ООП).
Постановка задачи
Предположим, что парсер принимает на входе арифметическое выражение, представляющее собой обычную строку вида: (x+10.2)^2+5*y-z. Входное выражение является правильным с точки зрения грамматики арифметических выражений:
- Количество открывающих скобок равно количеству закрывающих.
- Целая часть числа отделена от дробной с помощью точки.
- В строке присутствуют только допустимые символы: цифры 0...9, операторы +-*/^, скобки, точка и параметры x, y, z.
Парсер должен построить дерево лексем, пригодное для вычисления численного значения входного выражения. Значения параметров будем передавать методу, реализующему расчет численного значения.
Для каждого конкретного выражения дерево объектов строится один раз. Затем, используя полученное дерево объектов, вычисляем итоговое значение выходного выражения с учетом значений параметров. Повторять вычисления можно неограниченное число раз.
Алгоритм должен позволить обработку входных выражений неограниченной длины (в разумных пределах) без ограничений по уровню вложенности скобок.
Лексический анализ входного выражения
Перед тем как приступить непосредственно к парсингу входного выражения, желательно удалить незначащие символы (такие как пробел и т.п.) и сформировать цельные лексемы. Данная процедура не является обязательной в рамках алгоритма, однако позволяет существенно упростить понимание самого алгоритма и его программную реализацию.
Для примера, вернёмся к рассмотрению строки арифметического выражения, приведённую выше: (x+10.2)^2+5*y-z. В процессе лексического анализа указанная строка будет преобразована в массив строк следующей структуры: [0]=>”(”, [1]=>”x”, [2]=>”+”, [3]=>”10.2”, [4]=>”)”, [5]=>”^”, [6]=>”2”, [7]=>”+”, [8]=>”5”, [9]=>”*”, [10]=>”y”, [11]=>”-”, [12]=>”z”.
Таким образом, цельная лексема представляет из себя либо оператор (арифметическую операцию), либо операнд (число, состоящее из одной или нескольких цифр), либо параметр (x, y, z) или скобку (как элемент, изменяющий приоритет выполнения арифметических операций в строке).
Лексема как объект
Каждая цельная лексема в составе древовидной структуры описывается объектом. Любой объект «дерева» обладает набором свойств (полей) и определенным поведением. Перечислим предполагаемый набор полей данных для каждого объекта, моделирующего лексему:
- Поле name — определяет уникальное имя объекта.
- Поле lec — массив лексем, для хранения информации о той части входного выражения вершиной которого является данный узел «дерева» объектов.
- Поле const — если данный объект представляет собой параметр, тогда переменная хранит его наименование.
- Поле var — если данный объект представляет собой число или параметр, то переменная хранит его значение.
Поведение каждого объекта характеризуется совокупностью методов. Для данного случая достаточно одного метода, например: calc(). Если объект описывает поведение операнда (числа) или параметра, то необходимо чтобы он возвращал это число или значение параметра. Если объект описывает лексему, являющуюся одним из операторов (арифметические операции), тогда метод должен возвращать результат применения данного оператора к двум числам.
Все объекты древовидной структуры могут принадлежать одному классу, достаточно просто переопределить один метод при создании объекта. Или, как вариант, можно описать абстрактный класс с одной абстрактной функцией calc(). Далее для каждого типа лексемы опишем свой класс, наследующий абстрактный класс и определяющий конкретное поведение метода calc(). В примере программной реализации выбран последний способ, для которого требуется существенно меньший объём кода.
Некоторые поля могут оставаться незаполненными — это зависит от того, какую лексему моделирует данный конкретный объект.
Лексема как узел древовидной структуры
Конфигурация объектов, моделирующих лексемы в общих чертах ясна. Но тут возникает вопрос о том, как сформировать из этих объектов древовидную структуру?
Данная проблема довольно типична для проектов программного обеспечения. Суть решения можно получить из шаблона проектирования с названием: «Компоновщик». Слепое копирование всех тонкостей данного шаблона проектирования (паттерна) не входит в наши планы, поэтому пытаемся выделить самое главное и необходимое для конкретного случая.
Для компоновки объектов в древовидную структуру добавим в каждый объект еще три поля:
- Поле childrenLeft — левый «наследник» данного объекта.
- Поле childrenRight — правый «наследник» данного объекта.
- Поле parent — «родитель» данного объекта.
Здесь и далее термины «родитель» и «наследник» используются без привязки к одному из ключевых принципов ООП, а в контексте указания на относительное местоположение других объектов относительно заданного в сформированной древовидной структуре.
Чтобы пояснить сказанное, приведём изображение древовидной структуры для выражения «(x+10.2)^2+5*y-z», указав значения всех полей объектов.
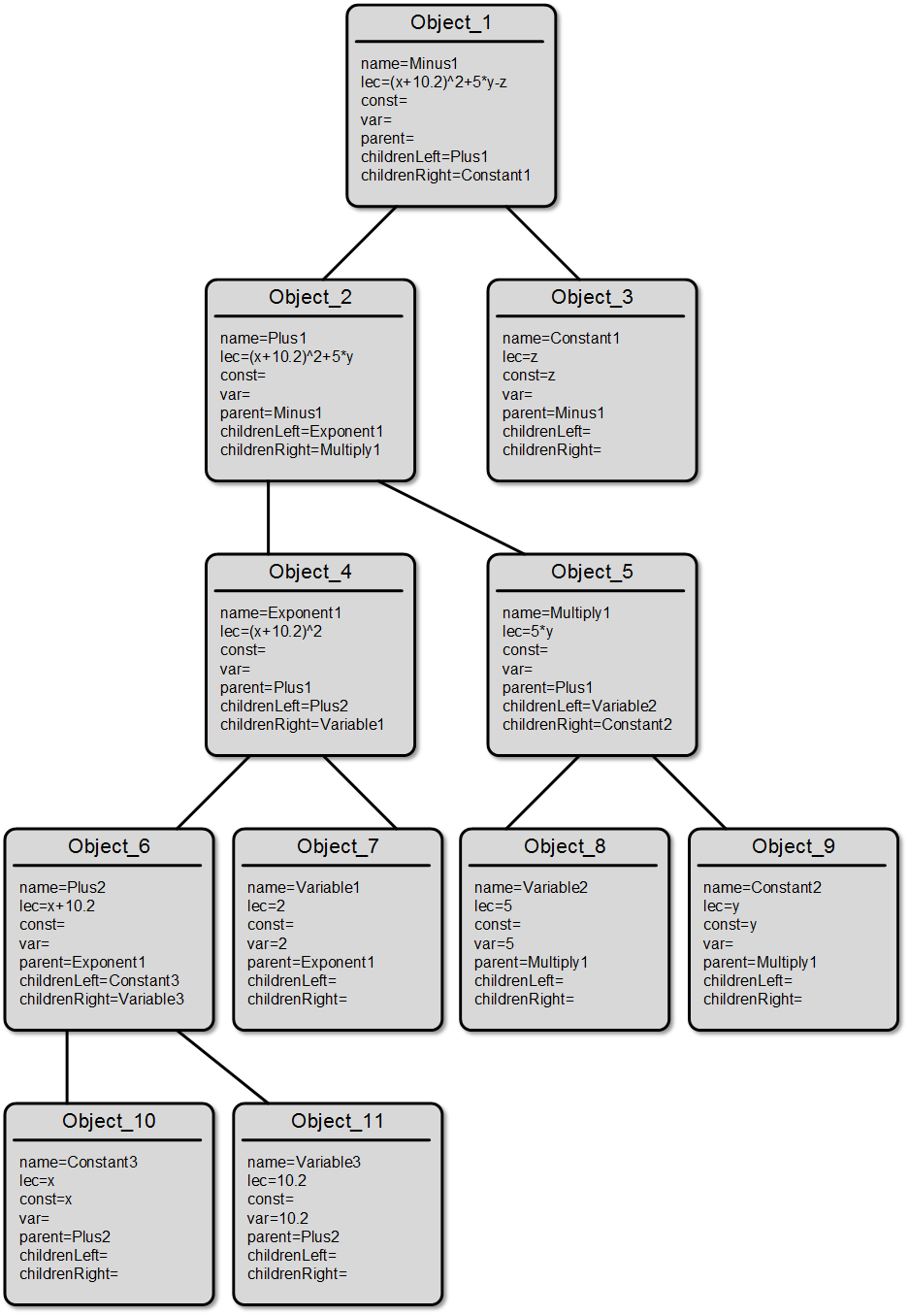
Из приведённой схемы становится предельно ясно, почему каждый узел может иметь только двоих «наследников», или не иметь их совсем.
Полученная структура объектов вполне приемлема для расчета значений арифметических выражений посредством вызова метода calc() самого верхнего на схеме объекта.
Поиск точки «перегиба» арифметического выражения
Под точкой «перегиба» арифметического выражения будем понимать один из элементов массива лексем, являющийся оператором (арифметическим действием) и имеющем максимальное значение при��ритета по отношению к другим операторам.
Для ввода возможности оценивать значения приоритетов арифметических операций в программе достаточно определить массив со структурой: [+]=>3, [-]=>3, [*]=>2, [/]=>2, [^]=>1.
Если значение приоритета максимально у нескольких операторов, следует выбирать последний из них, это позволит сформировать древовидную структуру корректно вычисляющую численные значения.
Далее в массиве лексем выделяются элементы, стоящие слева от точки «перегиба» и записываются в поле lec объекта, являющегося левым «наследником». Элементы, расположенные справа от точки «перегиба» заносятся в аналогичное поле правого «наследника». Следует так же упомянуть, что при поиске точки «перегиба» следует учитывать уровень вложенности скобок в массиве цельных лексем.
Построение древовидной структуры
В данном разделе подробно разберём последовательность формирования «дерева» объектов в рамках предложенного алгоритма.
Рассмотрим процедуру построения первых трёх объектов «дерева», включая корневой объект и его двоих «наследников». Получив на входе массив цельных лексем всего арифметического выражения, находим в нём точку «перегиба». Напомню, что это всегда оператор (арифметическое действие). Значение найденной точки «перегиба» позволяет однозначно определить класс объекта, находящегося на вершине структуры. Далее делим массив лексем на две части, как было описано выше. В каждой из обеих частей так же находим точки «перегиба», которые указывают на класс объектов левого и правого «наследников». Теперь можно сформировать все три объекта и указать связи между ними. В завершение объекты помещают в массив arNode для последующих действий над ними.
Для нашего входного выражения: (x+10.2)^2+5*y-z описанная процедура выглядит следующим образом. Под определение точки «перегиба» подпадают два оператора: «+» (между цифрами «2» и «5») и «-». Выбираем последний оператор в перечне: «-». Значение этого оператора позволяет выбрать необходимый класс корневого объекта и его имя. В частности, формируется объект класса Minus с именем Minus1. После деления исходного массива лексем на две части получаем два массива из элементов: (x+10.2)^2+5*y и z. Для первой лексемы точка перегиба "+", а вторая состоит только из одного элемента z. Это значит, что в качестве «наследников» корневого объекта следует сформировать объекты классов Plus и Constant с именами Plus1 и Constant1 соответственно. Осталось заполнить поля вновь созданных объектов: childrenLeft, childrenRight и parent для формирования древовидной структуры и внести объекты в массив arNode.
Дальнейшее формирование «дерева» очень похоже на процедуру создания первой тройки, но имеет свои тонкости. В массиве arNode простым перебором по элементам массива ищем объект с полем lec, содержащем более одного элемента в массиве и одновременно с пустыми полями childrenLeft и childrenRight. Считываем значение поля lec у выбранного объекта, делим его на две части в точке «перегиба». Далее находим точки «перегиба» у получившихся обеих частей и формируем два объекта-наследника для выбранного объекта, в соответствии с логикой изложенной выше. Не забываем формировать связи между объектами и добавлять сами объекты в массив arNode.
Указанную последовательность действий повторяем до тех пор, пока ни один из объектов древовидной структуры не будет соответствовать указанным условиям. Теперь можно считать, что «дерево» для нашего входного выражения построено и готово для вычисления значений.
Вычисление значений
Процесс вычисления значений входного арифметического выражения становится предельно ясен при просмотре листинга программной реализации алгоритма. Остановимся на некоторых существенных моментах.
Расчет происходит после вызова метода calc() объекта класса Main. В программе предусмотрена возможность использования не более трех параметров при вызове данного метода: x, y, z. Несложно это количество изменить с учетом потребностей конкретного применения описанного алгоритма.
Предварительно метод ищет в массиве объекты, описывающие лексемы параметров, затем в поля var найденных объектов заносятся числовые значения, указанные при вызове метода calc(). Теперь можно приступать к поиску в массиве arNode объекта с пустым полем parent (это будет корневой объект древовидной структуры) и вызвать его метод calc(). Метод возвращает значение арифметического выражения.
Пример программной реализации
Листинг программной реализации решено выложить целиком. Это позволяет скопировать программу целиком при необходимости проведения с ней экспериментов или доработки.
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title>Алгоритм</title>
</head>
<body>
<?php
class Main {
// массив объектов дерева
var $arNode = Array();
// расчет значения с учетом параметров
public function calc($x, $y, $z){
if($x){
foreach ($this->arNode as $obj){
if($obj->const == "x"){
$obj->var = $x;
break;
}
}
}
if($y){
foreach ($this->arNode as $obj){
if($obj->const == "y"){
$obj->var = $y;
break;
}
}
}
if($z){
foreach ($this->arNode as $obj){
if($obj->const == "z"){
$obj->var = $z;
break;
}
}
}
foreach ($this->arNode as $obj){
if(!$obj->parent){
return $obj->calc();
}
}
}
// реализация строительства дерева классов
public function builder ($str) {
// массив объектов дерева
$arNode = Array();
// предварительные операции с входной строкой
function parse ($str){
// подготовка входного выражения к парсингу
$str = mb_strtolower($str, 'UTF-8');
$str = str_replace(" ", "", $str);
$n = mb_strlen($str, 'UTF-8');
$arStr = preg_split('/(?!^)(?=.)/u', $str);
echo '<pre>';
echo print_r($arStr);
echo '</pre>';
// преобразуем массив символов в массив лексем
$j=0;
$accum = $arStr[0];
for($i=1; $i<$n+1; ++$i){
if ($i==$n+1){
$arLec[$j] = $accum;
break;
}
if($accum=="-" && $i==1){
if(preg_match("/\d/", $arStr[$i])){
$accum = $accum.$arStr[$i];
}
if($arStr[$i]=="("){
$arLec[$j] = "0";
$arLec[++$j] = "-";
++$j;
$accum = $arStr[$i];
}
continue;
}
if($accum=="-" && $arLec[$j-1]=="("){
$accum = $accum.$arStr[$i];
continue;
}
if (preg_match("/^[\d.]/", $accum) && preg_match("/^[\d.]/", $arStr[$i])){
$accum = $accum.$arStr[$i];
}else{
$arLec[$j] = $accum;
++$j;
$accum = $arStr[$i];
}
}
/*
$j = 0;
if($arStr[0]=="-"){
$accum = $arStr[0];
}else{
$accum = $arStr[0];
}
for ($i=1; $i<$n+1; ++$i){
if ($i==$n+1){
$arLec[$j] = $accum;
continue;
}
if (preg_match("/^[\d.]/", $accum)&&preg_match("/^[\d.]/", $arStr[$i])){
$accum = $accum.$arStr[$i];
}else{
$arLec[$j] = $accum;
++$j;
$accum = $arStr[$i];
}
}
*
*/
echo '<pre>';
echo print_r($arLec);
echo '</pre>';
return $arLec;
}
// построение одного объекта
function objBuilder($point){
static $arNumNode = Array(
"addition" => 1,
"subtraction" => 1,
"exponentiation" =>1,
"multiplication" => 1,
"division" => 1,
"number" => 1,
"constant" => 1);
switch ($point){
case "+": $name = "Plus".$arNumNode["addition"];
$node = new Plus($name);
++$arNumNode["addition"];
break;
case "-": $name = "Minus".$arNumNode["subtraction"];
$node = new Minus($name);
++$arNumNode["subtraction"];
break;
case "*": $name = "Multiply".$arNumNode["multiplication"];
$node = new Multiply($name);
++$arNumNode["multiplication"];
break;
case "/": $name = "Fission".$arNumNode["division"];
$node = new Fission($name);
++$arNumNode["division"];
break;
case "^": $name = "Exponent".$arNumNode["exponentiation"];
$node = new Exponent($name);
++$arNumNode["exponentiation"];
break;
case "x": $name = "Constant".$arNumNode["constant"];
$node = new Constant($name);
$node->const = "x";
$node->var = 0;
++$arNumNode["constant"];
break;
case "y": $name = "Constant".$arNumNode["constant"];
$node = new Constant($name);
$node->const = "y";
$node->var = 0;
++$arNumNode["constant"];
break;
case "z": $name = "Constant".$arNumNode["constant"];
$node = new Constant($name);
$node->const = "z";
$node->var = 0;
++$arNumNode["constant"];
break;
default: $name = "Variable".$arNumNode["number"];
$node = new Variable($name);
$node->var = $point;
++$arNumNode["number"];
}
return $node;
}
// строительство тройки объектов дерева
function trioBuilder($topLec, $leftLec, $rightLec, $topP, $leftP, $rightP, $topObj){
// вершина тройки
if(!$topObj){
$topTrio = objBuilder($topP);
$topTrio->lec = $topLec;
} else {
$topTrio = $topObj;
}
// левая ветвь тройки
$leftTrio = objBuilder($leftP);
$leftTrio->lec = $leftLec;
// правая ветвь тройки
$rightTrio = objBuilder($rightP);
$rightTrio->lec = $rightLec;
// формирование тройки из объектов
$topTrio->childrenLeft = $leftTrio;
$topTrio->childrenRight = $rightTrio;
$leftTrio->parent = $topTrio;
$rightTrio->parent = $topTrio;
if(!$topObj){
$trio = Array($topTrio, $leftTrio, $rightTrio);
return $trio;
} else {
$duo = Array($leftTrio, $rightTrio);
return $duo;
}
}
// проверка на полное построение дерева
function stopBuild($arNode){
foreach ($arNode as $obj){
if($obj->lec[1] && !$obj->childrenLeft && !$obj->childrenRight){
return FALSE;
}
}
return TRUE;
}
// поиск вершины для следующей тройки
function searchObj($arNode){
foreach ($arNode as $obj){
if($obj->lec[1] && !$obj->childrenLeft && !$obj->childrenRight){
return $obj;
}
}
}
// определение точки перегиба выражения
function inflPoint($lec){
$infl=0;
$max=0;
static $br = 0;
static $arPrioritet = Array(
"+" => 3,
"-" => 3,
"*" => 2,
"/" => 2,
"^" => 1);
foreach ($lec as $key=>$value){
if(preg_match("/^[\d.]/", $value)){
continue;
}
if($value=="("){
++$br;
continue;
}
if($value==")"){
--$br;
continue;
}
if($arPrioritet[$value]-3*$br >= $max){
$max=$arPrioritet[$value]-3*$br;
$infl=$key;
}
}
return $infl;
}
$arLec = parse($str);
// первая тройка дерева
$topN = inflPoint($arLec);
$topP = $arLec[$topN];
$leftLec = array_slice($arLec, 0, $topN);
if($leftLec[0]=="(" && $leftLec[count($leftLec)-1]==")"){
array_shift($leftLec);
array_pop($leftLec);
}
$rightLec = array_slice($arLec, $topN+1);
if($rightLec[0]=="(" && $rightLec[count($rightLec)-1]==")"){
array_shift($rightLec);
array_pop($rightLec);
}
$leftN = inflPoint($leftLec);
$leftP = $leftLec[$leftN];
$rightN = inflPoint($rightLec);
$rightP = $rightLec[$rightN];
$trio = trioBuilder($arLec, $leftLec, $rightLec, $topP, $leftP, $rightP, NULL);
$arNode = $trio;
// все последующие тройки дерева
while (!stopBuild($arNode)){
$topTrio = searchObj($arNode);
$arLec = $topTrio->lec;
$topN = inflPoint($arLec);
$leftLec = array_slice($arLec, 0, $topN);
if($leftLec[0]=="(" && $leftLec[count($leftLec)-1]==")"){
array_shift($leftLec);
array_pop($leftLec);
}
$rightLec = array_slice($arLec, $topN+1);
if($rightLec[0]=="(" && $rightLec[count($rightLec)-1]==")"){
array_shift($rightLec);
array_pop($rightLec);
}
$leftN = inflPoint($leftLec);
$leftP = $leftLec[$leftN];
$rightN = inflPoint($rightLec);
$rightP = $rightLec[$rightN];
$duo = trioBuilder(NULL, $leftLec, $rightLec, NULL, $leftP, $rightP, $topTrio);
$arNode = array_merge($arNode, $duo);
}
$this->arNode = $arNode;
}
}
abstract class Term {
public $name;
public $childrenLeft;
public $childrenRight;
public $parent;
public $lec;
public $const;
public $var;
public function __construct($name) {
$this->name = $name;
}
abstract function calc();
}
class Plus extends Term {
public function calc() {
return $this->childrenLeft->calc()+$this->childrenRight->calc();
}
}
class Minus extends Term {
public function calc() {
return $this->childrenLeft->calc()-$this->childrenRight->calc();
}
}
class Multiply extends Term {
public function calc() {
return $this->childrenLeft->calc()*$this->childrenRight->calc();
}
}
class Fission extends Term {
public function calc() {
return $this->childrenLeft->calc()/$this->childrenRight->calc();
}
}
class Exponent extends Term {
public function calc() {
return pow ($this->childrenLeft->calc(), $this->childrenRight->calc());
}
}
class Constant extends Term {
public function calc() {
return $this->var;
}
}
class Variable extends Term {
public function calc() {
return $this->var;
}
}
// задаем исходное математическое выражение
$str = "(x+10.2)^2+5*y-z";
$x = 2;
$y = 1;
$z = 3;
$parse = new Main();
// строительство дерева классов
$parse->builder($str);
//echo '<pre>';
//echo print_r($parse->arNode);
//echo '</pre>';
echo $str." = ".$parse->calc($x, $y, $z);
echo " при: x=".$x."; y=".$y."; z=".$z;
?>
</body>
</html>
Если убрать комментарии из трех идущих подряд операторов echo в конце программы, то можно проанализировать правильность формирования древовидной структуры и посмотреть значения полей всех объектов.
Заключение
Старался описать алгоритм по возможности подробно, но если остались вопросы — пишите, постараюсь всем ответить. Буду так же признателен за сообщения о найденных ошибках и неточностях в тексте.
