mathsatan 10 сен 2016 в 21:43

Аналитическое вычисление производной функции на языке Scala

7 мин

14K

Введение

Данный алгоритм реализован на языке Scala, характерной особенностью которого является использование case-классов, так удачно подходящих для написания алгоритма дифференцирования. В этой статье планируется описать лишь часть программы, содержащей алгоритм нахождения производной, поскольку разработка парсера для математических выражений это другая большая тема,
заслуживающая отдельной статьи

Подготовка

Сначала опишем структуру данных, в которой будет храниться исходная математическая функция. Опишем трейт MathAST:

sealed trait MathAST

И его наследников:

sealed trait SingleToken extends MathAST{
	val a: MathAST
}
sealed trait DoubleToken extends MathAST{
	val a: MathAST
	val b: MathAST
}
sealed trait LeafToken extends MathAST

SingleToken будет реализовывать case-классы унарных операторов, таких как sin(a), -a, ln(a) и т.д.
DoubleToken описывает бинарные операторы: a+b, a^b и т.д.
LeafToken — «листья» дерева, т.е. константы, переменные и зарезервированные имена констант (число Пи и экспонента).

Опишем классы/объекты операторов и токенов:

case object Pi extends LeafToken
case object Exponenta extends LeafToken

case class Sin(override val a: MathAST) extends SingleToken
case class Cos(override val a: MathAST) extends SingleToken
…
case class Mul(override val a: MathAST, override val b: MathAST) extends DoubleToken
case class Add(override val a: MathAST, override val b: MathAST) extends DoubleToken
…
case class Differentiate(f: MathAST, dx: Variable) extends MathAST

case class Variable(name: String) extends LeafToken
case class Constant(value: BigDecimal) extends LeafToken

Обратите внимание на класс Differentiate, он имеет особую сигнатуру: f – исходная функция, dx – переменная, по которой происходит дифференцирование.

Теперь есть все, чтобы представить математическую функцию в виде дерева вычислений, для примера возьмем функцию: 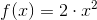$f(x)=2\cdot x^{2}$ , которая примет вид:

Mul(Constant(BigDecimal(2)), Pow(x, Constant(BigDecimal(2)))

Конечно, чтобы получить дерево-выражение из обычной строки, введенной пользователем, нужно написать парсер, но, как было упомянуто выше, это уже другая тема. Скажу лишь что в программе используется самодельный парсер, наследующий трейт Parsers из пакета scala.util.parsing.combinator.

Алгоритм нахождения производной

В основе которого лежат правила дифференцирования и таблица производных.

Опишем рекурсивную функцию, которая и будет преобразовывать исходную математическую функцию в результирующую функцию-производную:

def differentiate(f: MathAST)(implicit dx: String): MathAST

Аргумент dx, содержащий имя переменной (по которой происходит дифференцирование) помечен как неявный (implicit), это позволит не передавать ее в рекурсивные вызовы, пусть этим занимается компилятор.

На вход рекурсивной функции подается выражение — исходная функция f(x) (в формате MathAST), возвращаемое значение — функция-производная 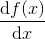$\frac{\mathrm{d} f(x)}{\mathrm{d} x}$ в том же формате.

Примечание 1: Выражение может быть бинарным, унарным или токеном.
Примечание 2: Оператором может быть один из: «+», «-», «^», «*», «/», «abs», «sin», «cos», «tg», «ctg», «ln», «arcsin», «arccos», «arctg», «arcctg», «(», «)».
Примечание 3: Входные и выходные данные представлены в формате MathAST — дерево-выражение.

Общий алгоритм

В общем виде алгоритм слишком абстрактный, поэтому дальше разберем его подробнее.

Рекурсивная функция получает на вход данные и используя сопоставление с образцом (pattern-matching) выполняет необходимые действия, в зависимости от типа данных.
Функция высчитывает производную для входного выражения и возвращает выражение-результат. Может получиться, что аргументы a и/или b оказались не константой и не переменной, а сложной функцией u(x),
тогда понадобится рекурсивно посчитать еще и производную u’(x), т.е. вернуть [ differentiate(u(x)) ] — перейти к шагу 1 с новыми данными — u(x).
Если данные не корректны вернуть сообщение об ошибке.

Детали принципа работы и связь с математическими абстракциями

Функция приняла на вход данные — выражение-функцию, которую следует обработать в соответствии с правилами дифференцирования

Если бинарное выражение

Бинарные выражения помечены трейтом DoubleToken. Оператор проверяется на соответствие одному из доступных операторов («+», «-», «*», «/», «^»):

case Add(a, b) => Add(differentiate(a), differentiate(b))
case Sub(a, b) => Sub(differentiate(a), differentiate(b))
…

Если оператор «+»: вернуть [ differentiate(a) + differentiate(b) ].
Если оператор «-»: вернуть [ differentiate(a) — differentiate(b) ].
Если оператор «*»: Умножение представляет из себя более сложный случай, операнды a и b могут быть константами или переменными (всего 4 комбинации: u(x)*c, u(x)*v(x), c*c, c*u(x)).
Функция анализирует какой из 4 вариантов попался и возвращает выражение используя правило дифференцирования № 1, № 3, и №5,
если один из операндов – сложная функция. Например: если a = u(x), а b = v(x), то вернуть [ differentiate(a) * b + a * differentiate(b)) ].
Приватный метод isDependsOnVar проверяет, зависит ли подвыражение от переменной, по которой производится дифференцирование.
Если оператор «/»: Действия аналогичны, как и с оператором «*».
Если оператор возведения в степень «^»: Здесь имеется так же 4 варианта выражений: u(x)^c, u(x)^v(x), c^c, c^u(x).
Третий случай самый нетривиальный: u(x)^v(x), чтобы найти производную от такого выражения нужно использовать логарифм и его свойства (описание процедуры логарифмирования выходит за рамки этой статьи, поэтому сразу приведем готовую формулу – № 6).

В остальных трех случаях используются стандартные табличные формулы.

В качестве примера приведем обработку операции умножения:


case Mul(a, b) => {
	val u = isDependsOnVar(a)
	val v = isDependsOnVar(b)
	if (u && !v) {
		Mul(differentiate(a), b)
	} else if (!u && v){    // c^u(x), c=const
		Mul(a, differentiate(b))
	}else if (!u && !v){    // c^c, c=const
		Constant(BigDecimal(0))
	}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}

Если унарное выражение

Классы SingleToken обрабатываются следующим образом:


case e: SingleToken =>
val d = e match {
	case Sin(x) => Cos(x)
	case Cos(x) => Usub(Sin(x))
	case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
	…
}
if (isLeaf(e.a)) d else Mul(d, differentiate(e.a))

Оператор проверяется на соответствие одному из доступных операторов («sin», «-», «cos», …)
Для примера, оператор «sin»: вернуть [ cos(a) ], если a = x, если же a — сложная функция u(x), то вернуть [ cos(a) * differentiate(a) ].

С остальными операторами происходят аналогичные действия, используя правило дифференцирования сложной функции и табличные правила взятия производной.

Отдельно следует рассмотреть оператор abs — модуль, поскольку его нет в таблице.

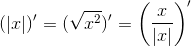
$(|x|)'=(\sqrt{x^{2}})'=\left( \dfrac{x}{|x|} \right)'$

Приватный метод isLeaf выясняет сложная функция или нет, в первом случае нужно вернуть текущий результат умноженный на производную вложенной функции, а во втором просто вернуть текущий результат.

Если один токен

Речь идет о переменной или константе

case Variable(a) => if (a == dx) Constant(BigDecimal(1)) else Constant(BigDecimal(0))
case Constant(a) => Constant(BigDecimal(0))
case Pi | Exponenta => Constant(BigDecimal(0))
case _ => throw new AbstractEvaluateException("Differentiate: Wrong input data")

Введены некорректные данные, вывести сообщение об ошибке и завершить работу.
Если переменная (по которой осуществляется дифференцирование, например x), вернуть [ 1 ].
Если константа, вернуть [ 0 ].

Напоследок добавим строку:

case Differentiate(_f, _dx) => differentiate(_f)(_dx.name)

Это на случай, если внутри функции есть вложенная производная, т.е. теперь можно считать производные высших порядков.

Приведу весь код дифференцирования, для лучшего понимания:

object Derivative {
  def apply(e: MathAST)(implicit dx: String): MathAST = differentiate(e)

  def differentiate(f: MathAST)(implicit dx: String): MathAST = f match {
    case Differentiate(_f, _dx) => differentiate(_f)(_dx.name)

    case Add(a, b) => Add(differentiate(a), differentiate(b))
    case Sub(a, b) => Sub(differentiate(a), differentiate(b))
    case Div(a, b) => Div(Sub(Mul(differentiate(a), b), Mul(a, differentiate(b))), Pow(b, Constant(BigDecimal(2))))

    case Pow(a, b) => {
      val u = isDependsOnVar(a)
      val v = isDependsOnVar(b)
      if (u && !v) Mul(Mul(Pow(a, Sub(b, Constant(BigDecimal(1)))), differentiate(a)), b) // u(x)^c, c=const
      else if (!u && v){  // c^u(x), c=const
        Mul(Mul(Pow(a, b), differentiate(b)), Ln(a))
      }else if(!u && !v){
        Constant(BigDecimal(0))
      }else Mul(Pow(a, Sub(b, Constant(BigDecimal(1)))), Add(Mul(b, differentiate(a)), Mul(Mul(a, Ln(a)), differentiate(b))))
    }
    case Mul(a, b) => {
      val u = isDependsOnVar(a)
      val v = isDependsOnVar(b)
      if (u && !v) {
        Mul(differentiate(a), b)
      } else if (!u && v){  // c^u(x), c=const
        Mul(a, differentiate(b))
      }else if (!u && !v){// c^c, c=const
        Constant(BigDecimal(0))
      }else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
    }

    case e: SingleToken =>
      val d = e match {
        case Sin(x) => Cos(x)
        case Cos(x) => Usub(Sin(x))
        case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
        case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
        case Abs(x) => Div(x, Abs(x))
        case Ln(x) => Div(Constant(BigDecimal(1)), x)
        case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
        case Usub(x) => Usub(differentiate(x))
        case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
        case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
        case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
        case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
        case _ => throw new AbstractEvaluateException("Differentiate: Unknown unary operator")
      }
      if (isLeaf(e.a)) d else Mul(d, differentiate(e.a))

    case Variable(a) => if (a == dx) Constant(BigDecimal(1)) else Constant(BigDecimal(0))
    case Constant(a) => Constant(BigDecimal(0))
    case Pi | Exponenta => Constant(BigDecimal(0))
    case _ => throw new AbstractEvaluateException("Differentiate: Wrong input data")
  }

  private def isLeaf(e: MathAST): Boolean = e match {
    case Variable(_) | Constant(_) => true
    case  Pi | Exponenta => true
    case _ => false
  }

  private def isDependsOnVar(tree: MathAST)(implicit dx: String): Boolean = tree match{
    case e: DoubleToken => (e.a match {
      case Variable(name) => if(name == dx) true else false
      case _ => isDependsOnVar(e.a)
    })||(e.b match {
      case Variable(name) => if(name == dx) true else false
      case _ => isDependsOnVar(e.b)
    })
    case e: SingleToken => isDependsOnVar(e.a)
    case Variable(name) => if(name == dx) true else false
    case _ => false
  }
}

Заключение

Весь код исходников можно скачать на github'е, протестировать программу онлайн можно на сайте Калькулятор производных онлайн, приложение выполнено в виде REST сервиса и дополнено модулями упрощения выражений.

Список литературы

Математический портал «mathprofi.ru» mathprofi.ru/slozhnye_proizvodnye_logarifmicheskaja_proizvodnaja.html
Odersky M. «Programming in Scala (second edition)»
Хостманн К. «Scala для нетерпеливых»

Хабы: