Теория игр — математическая дисциплина, рассматривающая моделирование действий игроков, которые имеют цель, заключающуюся в выбор оптимальных стратегий поведения в условиях конфликта. На Хабре эта тема уже освещалась, но сегодня мы поговорим о некоторых ее аспектах подробнее и рассмотрим примеры на Kotlin.
Так вот, стратегия – это совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации. Оптимальная стратегия игрока – стратегия, обеспечивающая наилучшее положение в данной игре, т.е. максимальный выигрыш. Если игра повторяется неоднократно и содержит, кроме личных, случайные ходы, то оптимальная стратегия обеспечивает максимальный средний выигрыш.
Задача теории игр – выявление оптимальных стратегий игроков. Основное предположение, исходя из которого находятся оптимальные стратегии, заключается в том, что противник (или противники) не менее разумен, чем сам игрок, и делает все для того, чтобы добиться своей цели. Расчет на разумного противника – лишь одна из потенциальных позиций в конфликте, но в теории игр именно она кладется в основу.
Существуют игры с природой в которых есть только один участник, максимизирующий свою прибыль. Игры с природой – математические модели, в которых выбор решения зависит об объективной действительности. Например, покупательский спрос, состояние природы и т.д. «Природа» – это обобщенное понятие не преследующего собственных целей противника. В таком случае для выбора оптимальной стратегии используется несколько критериев.
Различают два вида задач в играх с природой:
Кратко об этих критериях рассказано здесь.
Сейчас мы рассмотрим критерии принятия решений в чистых стратегиях, а в конце статьи решим игру в смешанных стратегиях аналитическим методом.
Все критерии принятия решений мы разберем на сквозном примере. Задача такова: фермеру необходимо определить, в каких пропорциях засеять свое поле тремя культурами, если урожайность этих культур, а, значит, и прибыль, зависят от того, каким будет лето: прохладным и дождливым, нормальным, или жарким и сухим. Фермер подсчитал чистую прибыль с 1 гектара от разных культур в зависимости от погоды. Игра определяется следующей матрицей:
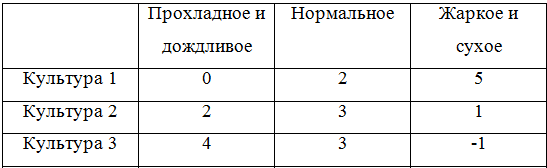
Далее эту матрицу будем представлять в виде стратегий:
Искомую оптимальную стратегию обозначим . Решать игру будем с помощью критериев Вальда, оптимизма, пессимизма, Сэвиджа и Гурвица в условиях неопределенности и критериев Байеса и Лапласа в условиях риска.
. Решать игру будем с помощью критериев Вальда, оптимизма, пессимизма, Сэвиджа и Гурвица в условиях неопределенности и критериев Байеса и Лапласа в условиях риска.
Как и говорилось выше примеры будут на Kotlin. Замечу, что вообще-то существуют такие решения как Gambit (написан на С), Axelrod и PyNFG (написанные на Python), но мы будем ехать на своем собственном велосипеде, собранном на коленке, просто ради того, чтобы немного потыкать стильный, модный и молодежный язык программирования.
Чтобы программно реализовать решение игры заведем несколько классов. Сначала нам понадобится класс, позволяющий описать строку или столбец игровой матрицы. Класс крайне простой и содержит список возможных значений (альтернатив или состояний природы) и соответствующего им имени. Поле
Игровая матрица содержит информацию об альтернативах и состояниях природы. Кроме того в ней реализованы некоторые методы, например нахождение доминирующего множества и чистой цены игры.
Опишем интерфейс, соответствующий критерию
Принятие решений в условиях неопределённости предполагает, что игроку не противостоит разумный противник.
В критерии Вальда максимизируется наихудший из возможных результатов:
Использование критерия страхует от наихудшего результата, но цена такой стратегии – потеря возможности получить наилучший из возможных результатов.
Рассмотрим пример. Для стратегий найдем минимумы и получим следующую тройку
найдем минимумы и получим следующую тройку  . Максимумом для указанной тройки будет являться значение 1, следовательно, по критерию Вальда выигрышной стратегией является стратегия
. Максимумом для указанной тройки будет являться значение 1, следовательно, по критерию Вальда выигрышной стратегией является стратегия  , соответствующая посадке Культуры 2.
, соответствующая посадке Культуры 2.
Программная реализация критерия Вальда незатейлива:
Для большей понятности в первый раз покажу, как решение выглядело бы в виде теста:
Нетрудно догадаться, что для других критериев отличие будет только в создании объекта
При использовании критерия оптимиста игрок выбирает решение, дающее лучший результат, при этом оптимист предполагает, что условия игры будут для него наиболее благоприятными:
Стратегия оптимиста может привести к отрицательным последствиям, когда максимальное предложение совпадает с минимальным спросом – фирма может получить убытки при списании нереализованной продукции. В тоже время стратегия оптимиста имеет определённый смысл, например, не нужно заботиться о неудовлетворённых покупателях, поскольку любой возможный спрос всегда удовлетворяется, поэтому нет нужды поддерживать расположения покупателей. Если реализуется максимальный спрос, то стратегия оптимиста позволяет получить максимальную полезность в то время, как другие стратегии приведут к недополученной прибыли. Это даёт определённые конкурентные преимущества.
Рассмотрим пример. Для стратегий найдем найдем максимум и получим следующую тройку
найдем найдем максимум и получим следующую тройку  . Максимумом для указанной тройки будет являться значение 5, следовательно, по критерию оптимизма выигрышной стратегией является стратегия
. Максимумом для указанной тройки будет являться значение 5, следовательно, по критерию оптимизма выигрышной стратегией является стратегия  , соответствующая посадке Культуры 1.
, соответствующая посадке Культуры 1.
Реализация критерия оптимизма почти не отличается от критерия Вальда:
Данный критерий предназначен для выбора наименьшего элемента игровой матрицы из ее минимально возможных элементов:
Критерий пессимизма предполагает, что развитие событий будет неблагоприятным для лица, принимающего решение. При использовании этого критерия лицо принимающее решение ориентируется на возможн��ю потерю контроля над ситуацией, поэтому, старается исключить потенциальные риски выбирая вариант с минимальной доходностью.
Рассмотрим пример. Для стратегий найдем найдем минимум и получим следующую тройку
найдем найдем минимум и получим следующую тройку  . Минимумом для указанной тройки будет являться значение -1, следовательно, по критерию пессимизма выигрышной стратегией является стратегия
. Минимумом для указанной тройки будет являться значение -1, следовательно, по критерию пессимизма выигрышной стратегией является стратегия  , соответствующая посадке Культуры 3.
, соответствующая посадке Культуры 3.
После знакомства с критериями Вальда и оптимизма то, как будет выглядеть класс критерия пессимизма, думаю, легко догадаться:
Критерий Сэвиджа (критерий сожалеющего пессимиста) предполагает минимизацию наибольшей потерянной прибыли, иными словами минимизируется наибольшее сожаление по потерянной прибыли:
В данном случае S — это матрица сожалений.
Оптимальное решение по критерию Сэвиджа должно давать наименьшее сожаление из найденных на предыдущем шаге решения сожалений. Решение, соответствующее найденной полезности, будет оптимальным.
К особенностям полученного решения относятся гарантированное отсутствие самых больших разочарований и гарантированное снижение максимальных возможных выигрышей других игроков.
Рассмотрим пример. Для стратегий составим матрицу сожалений:
составим матрицу сожалений:
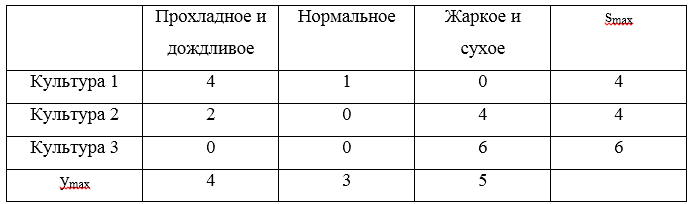
Тройка максимальных сожалений . Минимальным значением из указанных рисков будет являться значение 4, которое соответствует стратегиям
. Минимальным значением из указанных рисков будет являться значение 4, которое соответствует стратегиям  и
и  .
.
Запрограммировать критерий Сэвиджа немного сложнее:
Критерий Гурвица является регулируемым компромиссом между крайним пессимизмом и полным оптимизмом:
A(0) — стратегия крайнего пессимиста, A(k) — стратегия полного оптимиста, — задаваемое значение весового коэффициента:
— задаваемое значение весового коэффициента:  ;
;  — крайний пессимизм,
— крайний пессимизм,  — полный оптимизм.
— полный оптимизм.
При небольшом числе дискретных стратегий, задавая желаемое значение весового коэффициента , а затем округлять получаемый результат до ближайшего возможного значения с учётом выполненной дискретизации.
, а затем округлять получаемый результат до ближайшего возможного значения с учётом выполненной дискретизации.
Рассмотрим пример. Для стратегий . Примем, что коэффициент оптимизма
. Примем, что коэффициент оптимизма  . Теперь составим таблицу:
. Теперь составим таблицу:
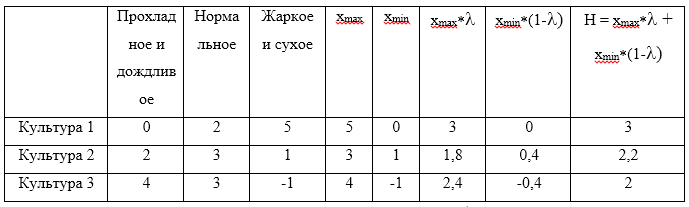
Максимальным значением из рассчитанных H будет являться значение 3, которое соответствует стратегии .
.
Реализация критерия Гурвица уже более объемная:
Методы принятия решений могут полагаться на критерии принятия решений в условиях риска при соблюдении следующих условий:
Если решение принимается в условиях риска, то стоимости альтернативных решений описываются вероятностными распределениями. В связи с этим принимаемое решение основывается на использовании критерия ожидаемого значения, в соответствии с которым альтернативные решения сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат.
Критерий ожидаемого значения может быть сведен либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат. В данном случае предполагается, что связанная с каждым альтернативным решением прибыль (затраты) является случайной величиной.
Постановка таких задач как правило такова: человек выбирает какие-либо действия в ситуации, где на результат действия влияют случайные события. Но игрок имеет некоторые знания о вероятностях этих событий и может рассчитать наиболее выгодную совокупность и очередность своих действий.
Чтобы можно было и дальше приводить примеры, дополним игровую матрицу вероятностями:
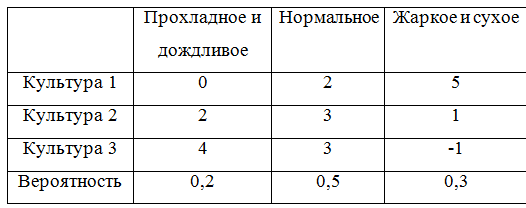
Для того, чтобы учесть вероятности придется немного переделать класс, описывающий игровую матрицу. Получилось, по правде говоря, не очень-то изящно, ну да ладно.
Критерий Байеса (критерий математического ожидания) используется в задачах принятия решения в условиях риска в качестве оценки стратегии выступает математическое ожидание соответствующей ей случайной величины. В соответствии с этим правилом оптимальная стратегия игрока
выступает математическое ожидание соответствующей ей случайной величины. В соответствии с этим правилом оптимальная стратегия игрока  находится из условия:
находится из условия:
Иными словами, показателем неэффективности стратегии по критерию Байеса относительно рисков является среднее значение (математическое ожидание ожидание) рисков i-й строки матрицы
по критерию Байеса относительно рисков является среднее значение (математическое ожидание ожидание) рисков i-й строки матрицы  , вероятности которых, совпадают с вероятностями природы. Тогда оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия
, вероятности которых, совпадают с вероятностями природы. Тогда оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия  , обладающая минимальной неэффективностью то есть минимальным средним риском. Критерий Байеса эквивалентен относительно выигрышей и относительно рисков, т.е. если стратегия
, обладающая минимальной неэффективностью то есть минимальным средним риском. Критерий Байеса эквивалентен относительно выигрышей и относительно рисков, т.е. если стратегия  является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот.
является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот.
Перейдем к примеру и рассчитаем матем��тические ожидания:
Максимальным математическим ожиданием является , следовательно, выигрышной стратегией является стратегия
, следовательно, выигрышной стратегией является стратегия  .
.
Программная реализация критерия Байеса:
Критерий Лапласа представляет упрощенную максимизацию математического ожидания полезности, когда справедливо предположение о равной вероятности уровней спроса, что избавляет от необходимости сбора реальной статистики.
В общем случае при использовании критерия Лапласа матрица ожидаемых полезностей и оптимальный критерий определяются следующим образом:
Рассмотрим пример принятия решений по критерию Лапласа. Рассчитаем среднеарифметическое для каждой стратегии:
Таким образом, выигрышной стратегией является стратегия .
.
Программная реализация критерия Лапласа:
Аналитический метод позволяет решить игру в смешанных стратегиях. Для того, чтобы сформулировать алгоритм нахождения решения игры аналитическим методом, рассмотрим некоторые дополнительные понятия.
Стратегия доминирует стратегию
доминирует стратегию  , если все
, если все  . Иными словами, если в некоторой строке платёжной матрицы все элементы больше или равны соответствующим элементам другой строки, то первая строка доминирует вторую и называется доминант-строкой. А также если в некотором столбце платёжной матрицы все элементы меньше или равны соответствующим элементам другого столбца, то первый столбец доминирует второй и называется доминант-столбцом.
. Иными словами, если в некоторой строке платёжной матрицы все элементы больше или равны соответствующим элементам другой строки, то первая строка доминирует вторую и называется доминант-строкой. А также если в некотором столбце платёжной матрицы все элементы меньше или равны соответствующим элементам другого столбца, то первый столбец доминирует второй и называется доминант-столбцом.
Нижней ценой игры называется .
.
Верхней ценой игры называется .
.
Теперь можно сформулировать алгоритм решения игры аналитическим методом:
Для того, чтобы привести пример необходимо привести класс, описывающий решение
И класс, выполняющий решение симплекс-методом. Поскольку в математике я не разбираюсь, то воспользовался готовой реализацией из Apache Commons Math
Теперь выполним решение аналитическим методом. Для наглядности возьмем другую игровую матрицу:
В этой матрице есть доминирующее множество:
\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}
Решение игры при цене игры равной 3,33
при цене игры равной 3,33
Надеюсь, эта статья будет полезна тем, кому необходимо в первом приближении с решением игр с природой. Вместо выводов ссылка на GitHub.
Буду благодарен за конструктивную обратную связь!
Так вот, стратегия – это совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации. Оптимальная стратегия игрока – стратегия, обеспечивающая наилучшее положение в данной игре, т.е. максимальный выигрыш. Если игра повторяется неоднократно и содержит, кроме личных, случайные ходы, то оптимальная стратегия обеспечивает максимальный средний выигрыш.
Задача теории игр – выявление оптимальных стратегий игроков. Основное предположение, исходя из которого находятся оптимальные стратегии, заключается в том, что противник (или противники) не менее разумен, чем сам игрок, и делает все для того, чтобы добиться своей цели. Расчет на разумного противника – лишь одна из потенциальных позиций в конфликте, но в теории игр именно она кладется в основу.
Существуют игры с природой в которых есть только один участник, максимизирующий свою прибыль. Игры с природой – математические модели, в которых выбор решения зависит об объективной действительности. Например, покупательский спрос, состояние природы и т.д. «Природа» – это обобщенное понятие не преследующего собственных целей противника. В таком случае для выбора оптимальной стратегии используется несколько критериев.
Различают два вида задач в играх с природой:
- задача о принятии решений в условиях риска, когда известны вероятности, с которыми природа принимает каждое из возможных состояний;
- задачи о принятии решений в условиях неопределенности, когда нет возможности получить информацию о вероятностях появления состояний природы.
Кратко об этих критериях рассказано здесь.
Сейчас мы рассмотрим критерии принятия решений в чистых стратегиях, а в конце статьи решим игру в смешанных стратегиях аналитическим методом.
Оговорочка
Я не являюсь специалистом в теории игр, а в этой работе использовал Kotlin в первый раз. Однако решил поделиться своими результатами. Если вы заметили ошибки в статье или хотите дать совет, прошу в личку.
Постановка задачи
Все критерии принятия решений мы разберем на сквозном примере. Задача такова: фермеру необходимо определить, в каких пропорциях засеять свое поле тремя культурами, если урожайность этих культур, а, значит, и прибыль, зависят от того, каким будет лето: прохладным и дождливым, нормальным, или жарким и сухим. Фермер подсчитал чистую прибыль с 1 гектара от разных культур в зависимости от погоды. Игра определяется следующей матрицей:

Далее эту матрицу будем представлять в виде стратегий:
Искомую оптимальную стратегию обозначим
Как и говорилось выше примеры будут на Kotlin. Замечу, что вообще-то существуют такие решения как Gambit (написан на С), Axelrod и PyNFG (написанные на Python), но мы будем ехать на своем собственном велосипеде, собранном на коленке, просто ради того, чтобы немного потыкать стильный, модный и молодежный язык программирования.
Чтобы программно реализовать решение игры заведем несколько классов. Сначала нам понадобится класс, позволяющий описать строку или столбец игровой матрицы. Класс крайне простой и содержит список возможных значений (альтернатив или состояний природы) и соответствующего им имени. Поле
key будем использовать для идентификации, а также при сравнении, а сравнение понадобится при реализации доминирования.Строка или столбец игровой матрицы
import java.text.DecimalFormat import java.text.NumberFormat open class GameVector(name: String, values: List<Double>, key: Int = -1) : Comparable<GameVector> { val name: String val values: List<Double> val key: Int private val formatter:NumberFormat = DecimalFormat("#0.00") init { this.name = name; this.values = values; this.key = key; } public fun max(): Double? { return values.max(); } public fun min(): Double? { return values.min(); } override fun toString(): String{ return name + ": " + values .map { v -> formatter.format(v) } .reduce( {f1: String, f2: String -> "$f1 $f2"}) } override fun compareTo(other: GameVector): Int { var compare = 0 if (this.key == other.key){ return compare } var great = true for (i in 0..this.values.lastIndex){ great = great && this.values[i] >= other.values[i] } if (great){ compare = 1 }else{ var less = true for (i in 0..this.values.lastIndex){ less = less && this.values[i] <= other.values[i] } if (less){ compare = -1 } } return compare } }
Игровая матрица содержит информацию об альтернативах и состояниях природы. Кроме того в ней реализованы некоторые методы, например нахождение доминирующего множества и чистой цены игры.
Игровая матрица
open class GameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>, natureStateNames: List<String>) { val matrix: List<List<Double>> val alternativeNames: List<String> val natureStateNames: List<String> val alternatives: List<GameVector> val natureStates: List<GameVector> init { this.matrix = matrix; this.alternativeNames = alternativeNames this.natureStateNames = natureStateNames var alts: MutableList<GameVector> = mutableListOf() for (i in 0..matrix.lastIndex) { val currAlternative = alternativeNames[i] val gameVector = GameVector(currAlternative, matrix[i], i) alts.add(gameVector) } alternatives = alts.toList() var nss: MutableList<GameVector> = mutableListOf() val lastIndex = matrix[0].lastIndex // нет провеврки на равенство длин всех строк, считаем что они равны for (j in 0..lastIndex) { val currState = natureStateNames[j] var states: MutableList<Double> = mutableListOf() for (i in 0..matrix.lastIndex) { states.add(matrix[i][j]) } val gameVector = GameVector(currState, states.toList(), j) nss.add(gameVector) } natureStates = nss.toList() } open fun change (i : Int, j : Int, value : Double) : GameMatrix{ var mml = this.matrix.toMutableList() var rowi = mml[i].toMutableList() rowi.set(j, value) mml.set(i, rowi) return GameMatrix(mml.toList(), alternativeNames, natureStateNames) } open fun changeAlternativeName (i : Int, value : String) : GameMatrix{ var list = alternativeNames.toMutableList() list.set(i, value) return GameMatrix(matrix, list.toList(), natureStateNames) } open fun changeNatureStateName (j : Int, value : String) : GameMatrix{ var list = natureStateNames.toMutableList() list.set(j, value) return GameMatrix(matrix, alternativeNames, list.toList()) } fun size() : Pair<Int, Int>{ return Pair(alternatives.size, natureStates.size) } override fun toString(): String { return "Состояния природы:\n" + natureStateNames.reduce { n1: String, n2: String -> "$n1;\n$n2" } + "\nМатрица игры:\n" + alternatives .map { a: GameVector -> a.toString() } .reduce { a1: String, a2: String -> "$a1;\n$a2" } } protected fun dominateSet(gvl: List<GameVector>, list: MutableList<String>, dvv: Int) : MutableSet<GameVector>{ var dSet: MutableSet<GameVector> = mutableSetOf() for (gv in gvl){ for (gvv in gvl){ if (!dSet.contains(gv) && !dSet.contains(gvv)) { if (gv.compareTo(gvv) == dvv) { dSet.add(gv) list.add("[$gvv] доминирует [$gv]") } } } } return dSet } open fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>) : GameMatrix{ var result: MutableList<MutableList<Double>> = mutableListOf() var ralternativeNames: MutableList<String> = mutableListOf() var rnatureStateNames: MutableList<String> = mutableListOf() val dIndex = dCol.map { c -> c.key }.toList() for (i in 0 .. natureStateNames.lastIndex){ if (!dIndex.contains(i)){ rnatureStateNames.add(natureStateNames[i]) } } for (gv in this.alternatives){ if (!dRow.contains(gv)){ var nr: MutableList<Double> = mutableListOf() for (i in 0 .. gv.values.lastIndex){ if (!dIndex.contains(i)){ nr.add(gv.values[i]) } } result.add(nr) ralternativeNames.add(gv.name) } } val rlist = result.map { r -> r.toList() }.toList() return GameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList()) } fun dominateMatrix(): Pair<GameMatrix, List<String>>{ var list: MutableList<String> = mutableListOf() var dCol: MutableSet<GameVector> = dominateSet(this.natureStates, list, 1) var dRow: MutableSet<GameVector> = dominateSet(this.alternatives, list, -1) val newMatrix = newMatrix(dCol, dRow) var ddgm = Pair(newMatrix, list.toList()) val ret = iterate(ddgm, list) return ret; } protected fun iterate(ddgm: Pair<GameMatrix, List<String>>, list: MutableList<String>) : Pair<GameMatrix, List<String>>{ var dgm = this var lddgm = ddgm while (dgm.size() != lddgm.first.size()){ dgm = lddgm.first list.addAll(lddgm.second) lddgm = dgm.dominateMatrix() } return Pair(dgm,list.toList().distinct()) } fun minClearPrice(): Double{ val map: List<Double> = this.alternatives.map { a -> a?.min() ?: 0.0 } return map?.max() ?: 0.0 } fun maxClearPrice(): Double{ val map: List<Double> = this.natureStates.map { a -> a?.max() ?: 0.0 } return map?.min() ?: 0.0 } fun existsClearStrategy() : Boolean{ return minClearPrice() >= maxClearPrice() } }
Опишем интерфейс, соответствующий критерию
Критерий
interface ICriteria { fun optimum(): List<GameVector> }
Принятие решений в условиях неопределенности
Принятие решений в условиях неопределённости предполагает, что игроку не противостоит разумный противник.
Критерий Вальда
В критерии Вальда максимизируется наихудший из возможных результатов:
Использование критерия страхует от наихудшего результата, но цена такой стратегии – потеря возможности получить наилучший из возможных результатов.
Рассмотрим пример. Для стратегий
Программная реализация критерия Вальда незатейлива:
class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } }
Для большей понятности в первый раз покажу, как решение выглядело бы в виде теста:
Тест
private fun matrix(): GameMatrix { val alternativeNames: List<String> = listOf("Культура 1", "Культура 2", "Культура 3") val natureStateNames: List<String> = listOf("Прохладное и дождливое", "Нормальное", "Жаркое и сухое") val matrix: List<List<Double>> = listOf( listOf(0.0, 2.0, 5.0), listOf(2.0, 3.0, 1.0), listOf(4.0, 3.0, -1.0) ) val gm = GameMatrix(matrix, alternativeNames, natureStateNames) return gm; } } private fun testCriteria(gameMatrix: GameMatrix, criteria: ICriteria, name: String){ println(gameMatrix.toString()) val optimum = criteria.optimum() println("$name. Оптимальная стратегия: ") optimum.forEach { o -> println(o.toString()) } } @Test fun testWaldCriteria() { val matrix = matrix(); val criteria = WaldCriteria(matrix) testCriteria(matrix, criteria, "Критерий Вальда") }
Нетрудно догадаться, что для других критериев отличие будет только в создании объекта
criteria.Критерий оптимизма
При использовании критерия оптимиста игрок выбирает решение, дающее лучший результат, при этом оптимист предполагает, что условия игры будут для него наиболее благоприятными:
Стратегия оптимиста может привести к отрицательным последствиям, когда максимальное предложение совпадает с минимальным спросом – фирма может получить убытки при списании нереализованной продукции. В тоже время стратегия оптимиста имеет определённый смысл, например, не нужно заботиться о неудовлетворённых покупателях, поскольку любой возможный спрос всегда удовлетворяется, поэтому нет нужды поддерживать расположения покупателей. Если реализуется максимальный спрос, то стратегия оптимиста позволяет получить максимальную полезность в то время, как другие стратегии приведут к недополученной прибыли. Это даёт определённые конкурентные преимущества.
Рассмотрим пример. Для стратегий
Реализация критерия оптимизма почти не отличается от критерия Вальда:
class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } }
Критерий пессимизма
Данный критерий предназначен для выбора наименьшего элемента игровой матрицы из ее минимально возможных элементов:
Критерий пессимизма предполагает, что развитие событий будет неблагоприятным для лица, принимающего решение. При использовании этого критерия лицо принимающее решение ориентируется на возможн��ю потерю контроля над ситуацией, поэтому, старается исключить потенциальные риски выбирая вариант с минимальной доходностью.
Рассмотрим пример. Для стратегий
После знакомства с критериями Вальда и оптимизма то, как будет выглядеть класс критерия пессимизма, думаю, легко догадаться:
class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == min!!.second } .map { m -> m.first } } }
Критерий Сэвиджа
Критерий Сэвиджа (критерий сожалеющего пессимиста) предполагает минимизацию наибольшей потерянной прибыли, иными словами минимизируется наибольшее сожаление по потерянной прибыли:
В данном случае S — это матрица сожалений.
Оптимальное решение по критерию Сэвиджа должно давать наименьшее сожаление из найденных на предыдущем шаге решения сожалений. Решение, соответствующее найденной полезности, будет оптимальным.
К особенностям полученного решения относятся гарантированное отсутствие самых больших разочарований и гарантированное снижение максимальных возможных выигрышей других игроков.
Рассмотрим пример. Для стратегий

Тройка максимальных сожалений
Запрограммировать критерий Сэвиджа немного сложнее:
class SavageCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.risk(): List<Pair<GameVector, Double?>> { val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) } .map { n -> n.first.key to n.second }.toMap() var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf() for (a in this.alternatives) { var v: MutableList<Double> = mutableListOf() for (i in 0..a.values.lastIndex) { val mn = maxStates.get(i) v.add(mn!! - a.values[i]) } am.add(Pair(a, v.toList())) } return am.map { m -> Pair(m.first, m.second.max()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.risk() val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == minRisk!!.second } .map { m -> m.first } } }
Критерий Гурвица
Критерий Гурвица является регулируемым компромиссом между крайним пессимизмом и полным оптимизмом:
A(0) — стратегия крайнего пессимиста, A(k) — стратегия полного оптимиста,
При небольшом числе дискретных стратегий, задавая желаемое значение весового коэффициента
Рассмотрим пример. Для стратегий

Максимальным значением из рассчитанных H будет являться значение 3, которое соответствует стратегии
Реализация критерия Гурвица уже более объемная:
class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria { val gameMatrix: GameMatrix val optimisticKoef: Double init { this.gameMatrix = gameMatrix this.optimisticKoef = optimisticKoef } inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){ val xmax: Double val xmin: Double val optXmax: Double val value: Double init{ this.xmax = xmax this.xmin = xmin this.optXmax = optXmax value = xmax * optXmax + xmin * (1 - optXmax) } } fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> { return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) } } override fun optimum(): List<GameVector> { val hpar = gameMatrix.getHurwitzParams() val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) }) return hpar .filter { r -> r.second == maxHurw!!.second } .map { m -> m.first } } }
Принятие решений в условиях риска
Методы принятия решений могут полагаться на критерии принятия решений в условиях риска при соблюдении следующих условий:
- отсутствия достоверной информации о возможных последствиях;
- наличия вероятностных распределений;
- знания вероятности наступления исходов или последствий для каждого решения.
Если решение принимается в условиях риска, то стоимости альтернативных решений описываются вероятностными распределениями. В связи с этим принимаемое решение основывается на использовании критерия ожидаемого значения, в соответствии с которым альтернативные решения сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат.
Критерий ожидаемого значения может быть сведен либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат. В данном случае предполагается, что связанная с каждым альтернативным решением прибыль (затраты) является случайной величиной.
Постановка таких задач как правило такова: человек выбирает какие-либо действия в ситуации, где на результат действия влияют случайные события. Но игрок имеет некоторые знания о вероятностях этих событий и может рассчитать наиболее выгодную совокупность и очередность своих действий.
Чтобы можно было и дальше приводить примеры, дополним игровую матрицу вероятностями:

Для того, чтобы учесть вероятности придется немного переделать класс, описывающий игровую матрицу. Получилось, по правде говоря, не очень-то изящно, ну да ладно.
Игровая матрица с вероятностями
open class ProbabilityGameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>, natureStateNames: List<String>, probabilities: List<Double>) : GameMatrix(matrix, alternativeNames, natureStateNames) { val probabilities: List<Double> init { this.probabilities = probabilities; } override fun change (i : Int, j : Int, value : Double) : GameMatrix{ val cm = super.change(i, j, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } override fun changeAlternativeName (i : Int, value : String) : GameMatrix{ val cm = super.changeAlternativeName(i, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } override fun changeNatureStateName (j : Int, value : String) : GameMatrix{ val cm = super.changeNatureStateName(j, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } fun changeProbability (j : Int, value : Double) : GameMatrix{ var list = probabilities.toMutableList() list.set(j, value) return ProbabilityGameMatrix(matrix, alternativeNames, natureStateNames, list.toList()) } override fun toString(): String { var s = "" val formatter: NumberFormat = DecimalFormat("#0.00") for (i in 0 .. natureStateNames.lastIndex){ s += natureStateNames[i] + " = " + formatter.format(probabilities[i]) + "\n" } return "Состояния природы:\n" + s + "Матрица игры:\n" + alternatives .map { a: GameVector -> a.toString() } .reduce { a1: String, a2: String -> "$a1;\n$a2" } } override fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>) : GameMatrix{ var result: MutableList<MutableList<Double>> = mutableListOf() var ralternativeNames: MutableList<String> = mutableListOf() var rnatureStateNames: MutableList<String> = mutableListOf() var rprobailities: MutableList<Double> = mutableListOf() val dIndex = dCol.map { c -> c.key }.toList() for (i in 0 .. natureStateNames.lastIndex){ if (!dIndex.contains(i)){ rnatureStateNames.add(natureStateNames[i]) } } for (i in 0 .. probabilities.lastIndex){ if (!dIndex.contains(i)){ rprobailities.add(probabilities[i]) } } for (gv in this.alternatives){ if (!dRow.contains(gv)){ var nr: MutableList<Double> = mutableListOf() for (i in 0 .. gv.values.lastIndex){ if (!dIndex.contains(i)){ nr.add(gv.values[i]) } } result.add(nr) ralternativeNames.add(gv.name) } } val rlist = result.map { r -> r.toList() }.toList() return ProbabilityGameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList(), rprobailities.toList()) } } }
Критерий Байеса
Критерий Байеса (критерий математического ожидания) используется в задачах принятия решения в условиях риска в качестве оценки стратегии
Иными словами, показателем неэффективности стратегии
Перейдем к примеру и рассчитаем матем��тические ожидания:
Максимальным математическим ожиданием является
Программная реализация критерия Байеса:
class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria { val gameMatrix: ProbabilityGameMatrix init { this.gameMatrix = gameMatrix } fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> { var am: MutableList<Pair<GameVector, Double>> = mutableListOf() for (a in this.alternatives) { var alprob: Double = 0.0 for (i in 0..a.values.lastIndex) { alprob += a.values[i] * this.probabilities[i] } am.add(Pair(a, alprob)) } return am.toList(); } override fun optimum(): List<GameVector> { val risk = gameMatrix.bayesProbability() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } }
Критерий Лапласа
Критерий Лапласа представляет упрощенную максимизацию математического ожидания полезности, когда справедливо предположение о равной вероятности уровней спроса, что избавляет от необходимости сбора реальной статистики.
В общем случае при использовании критерия Лапласа матрица ожидаемых полезностей и оптимальный критерий определяются следующим образом:
Рассмотрим пример принятия решений по критерию Лапласа. Рассчитаем среднеарифметическое для каждой стратегии:
Таким образом, выигрышной стратегией является стратегия
Программная реализация критерия Лапласа:
class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> { return this.alternatives.map { m -> Pair(m, m.values.average()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.arithemicMean() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } }
Смешанные стратегии. Аналитический метод
Аналитический метод позволяет решить игру в смешанных стратегиях. Для того, чтобы сформулировать алгоритм нахождения решения игры аналитическим методом, рассмотрим некоторые дополнительные понятия.
Стратегия
Нижней ценой игры называется
Верхней ценой игры называется
Теперь можно сформулировать алгоритм решения игры аналитическим методом:
- Вычислить нижнюю
и верхнюю
цены игры. Если
, то записать ответ в чистых стратегиях, если нет — продолжаем решение дальше
- Удалить доминирующие строки доминирующие столбцы. Их может быть несколько. На их место в оптимальной стратегии соответствующие компоненты будут равны 0
- Решить матричную игру методом линейного программирования.
Для того, чтобы привести пример необходимо привести класс, описывающий решение
Solve
class Solve(gamePriceObr: Double, solutions: List<Double>, names: List<String>) { val gamePrice: Double val gamePriceObr: Double val solutions: List<Double> val names: List<String> private val formatter: NumberFormat = DecimalFormat("#0.00") init{ this.gamePrice = 1 / gamePriceObr this.gamePriceObr = gamePriceObr; this.solutions = solutions this.names = names } override fun toString(): String{ var s = "Цена игры: " + formatter.format(gamePrice) + "\n" for (i in 0..solutions.lastIndex){ s += "$i) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "\n" } return s } fun itersect(matrix: GameMatrix): String{ var s = "Цена игры: " + formatter.format(gamePrice) + "\n" for (j in 0..matrix.alternativeNames.lastIndex) { var f = false val a = matrix.alternativeNames[j] for (i in 0..solutions.lastIndex) { if (a.equals(names[i])) { s += "$j) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "\n" f = true break } } if (!f){ s += "$j) " + a + " = 0\n" } } return s } }
И класс, выполняющий решение симплекс-методом. Поскольку в математике я не разбираюсь, то воспользовался готовой реализацией из Apache Commons Math
Solver
open class Solver (gameMatrix: GameMatrix) { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } fun solve(): Solve{ val goalf: List<Double> = gameMatrix.alternatives.map { a -> 1.0 } val f = LinearObjectiveFunction(goalf.toDoubleArray(), 0.0) val constraints = ArrayList<LinearConstraint>() for (alt in gameMatrix.alternatives){ constraints.add(LinearConstraint(alt.values.toDoubleArray(), Relationship.LEQ, 1.0)) } val solution = SimplexSolver().optimize(f, LinearConstraintSet(constraints), GoalType.MAXIMIZE, NonNegativeConstraint(true)) val sl: List<Double> = solution.getPoint().toList() val solve = Solve(solution.getValue(), sl, gameMatrix.alternativeNames) return solve } }
Теперь выполним решение аналитическим методом. Для наглядности возьмем другую игровую матрицу:
В этой матрице есть доминирующее множество:
\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}
Решение
val alternativeNames: List<String> = listOf("Культура 1", "Культура 2", "Культура 3") val natureStateNames: List<String> = listOf("Прохладное и дождливое", "Нормальное", "Жаркое и сухое", "Ветреное") val matrix: List<List<Double>> = listOf( listOf(2.0, 4.0, 8.0, 5.0), listOf(6.0, 2.0, 4.0, 6.0), listOf(3.0, 2.0, 5.0, 4.0) ) val gm = GameMatrix(matrix, alternativeNames, natureStateNames) val (dgm, list) = gm.dominateMatrix() println(dgm.toString()) println(list.reduce({s1, s2 -> s1 + "\n" + s2})) println() val s: Solver = Solver(dgm) val solve = s.solve() println(solve)
Решение игры
Вместо заключения
Надеюсь, эта статья будет полезна тем, кому необходимо в первом приближении с решением игр с природой. Вместо выводов ссылка на GitHub.
Буду благодарен за конструктивную обратную связь!
