Все мы знаем из школьного курса что такое системы счисления(СС). Но не все задумываются о том, на сколько затратны СС. Т.е. какой набор цифр нам необходим для представления числа в данной СС. Когда у нас есть ограниченный набор уникальных элементов (разноцветные камушки разных размеров), с помощью которого мы можем представить число, какое максимальное число мы можем представить используя эти элементы? (все красные камушки — это ноль, зелёные — один, синие — два и т.д., маленькие — нулевой разряд, средние — первый, большие — второй и т.д.). Где та грань, при которой основание СС играет большую роль чем разрядность числа?
Возьмём для примера n — количество элементов, равным 60. Разбив элементы на 2 группы (двоичная система счисления) мы получим 30 разрядов. 30 единиц — самое больше 30-ти разрядное число с основанием 2. Если к нему прибавить 1, то получим единицу с 30 нулями, т.е. 2 в 30-ой, так как каждый ноль — это степень двойки, а разряды начинаются с 0, и не забудем вычесть единицу, которую прибавили.
Для других СС аналогично
, где y — максимальное число, x — основание степени.
Точки построения:
.
.
График функции:
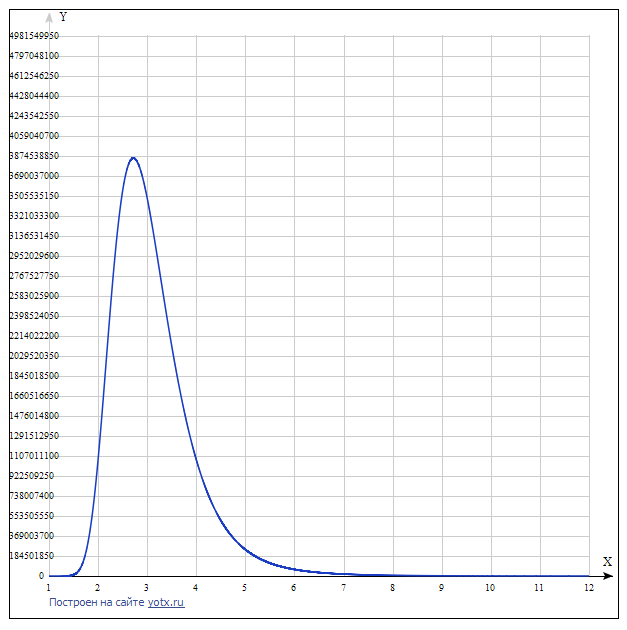
Из графика видно, что с увеличением основания СС, начиная с трёх, затратность её увеличивается и функция имеет верхний экстремум. Приведя её к общему виду можно получить![$y=(\sqrt[x]x)^{n}-1$](https://habrastorage.org/getpro/habr/formulas/759/8ad/ef6/7598adef600bb077d5798877d3f644cc.svg)
, а максимум функции ![$\sqrt[x]x$](https://habrastorage.org/getpro/habr/formulas/fc9/4eb/725/fc94eb72542b934f8fdde50bd59e1e31.svg)
достигается при 
.
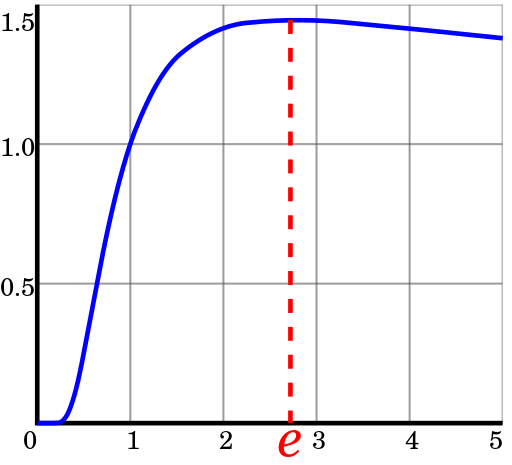
График функции![$y=\sqrt[x]x$](https://habrastorage.org/getpro/habr/formulas/1d8/10b/bc3/1d810bbc3c1459b77d2888393e7739c3.svg)
Т.е. самая экономичная СС — это система, максимально близкая к
или 3.
P.S.: По мимо того СС с основанием 3 — нечётная, а значит не имеет проблемы округления (привести 0.5 к 0 или к 1), а если цифры записывать симметрично (-1,0,1 вместо 0,1,2) то появляется простота представления отрицательных чисел (10-1 это 8, -101 это -8, где минус — это не знак, а часть цифры, которую можно заменить на Z), но это уже совсем другая арифметика)))
Возьмём для примера n — количество элементов, равным 60. Разбив элементы на 2 группы (двоичная система счисления) мы получим 30 разрядов. 30 единиц — самое больше 30-ти разрядное число с основанием 2. Если к нему прибавить 1, то получим единицу с 30 нулями, т.е. 2 в 30-ой, так как каждый ноль — это степень двойки, а разряды начинаются с 0, и не забудем вычесть единицу, которую прибавили.
Для других СС аналогично
, где y — максимальное число, x — основание степени.Точки построения:
. . График функции:
Из графика видно, что с увеличением основания СС, начиная с трёх, затратность её увеличивается и функция имеет верхний экстремум. Приведя её к общему виду можно получить
, а максимум функции достигается при .График функции
Т.е. самая экономичная СС — это система, максимально близкая к
или 3. P.S.: По мимо того СС с основанием 3 — нечётная, а значит не имеет проблемы округления (привести 0.5 к 0 или к 1), а если цифры записывать симметрично (-1,0,1 вместо 0,1,2) то появляется простота представления отрицательных чисел (10-1 это 8, -101 это -8, где минус — это не знак, а часть цифры, которую можно заменить на Z), но это уже совсем другая арифметика)))
