Yermack 13 ноя 2018 в 22:33

Julia и движение заряженной частицы в электромагнитном поле

6 мин

9.1K

Туториал

Закрепляем навыки решения и визуализации дифференциальных уравнений на примере одного из самых распространенных эволюционных уравнений, вспоминаем о старом-добром Scilab и пытаемся понять, а надо ли оно нам… Под катом картинки (килобайт на семьсот)

Удостоверимся в свежести софта

julia>]
(v1.0) pkg>update
#успеете заварить чаю
(v1.0) pkg> status
    Status `C:\Users\Игорь\.julia\environments\v1.0\Project.toml`
  [537997a7] AbstractPlotting v0.9.0
  [ad839575] Blink v0.8.1
  [159f3aea] Cairo v0.5.6
  [5ae59095] Colors v0.9.5
  [8f4d0f93] Conda v1.1.1
  [0c46a032] DifferentialEquations v5.3.1
  [a1bb12fb] Electron v0.3.0
  [5789e2e9] FileIO v1.0.2
  [5752ebe1] GMT v0.5.0
  [28b8d3ca] GR v0.35.0
  [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git)
  [4c0ca9eb] Gtk v0.16.4
  [a1b4810d] Hexagons v0.2.0
  [7073ff75] IJulia v1.14.1+ [`C:\Users\Игорь\.julia\dev\IJulia`]
  [6218d12a] ImageMagick v0.7.1
  [c601a237] Interact v0.9.0
  [b964fa9f] LaTeXStrings v1.0.3
  [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git)
  [7269a6da] MeshIO v0.3.1
  [47be7bcc] ORCA v0.2.0
  [58dd65bb] Plotly v0.2.0
  [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git)
  [91a5bcdd] Plots v0.21.0
  [438e738f] PyCall v1.18.5
  [d330b81b] PyPlot v2.6.3
  [c4c386cf] Rsvg v0.2.2
  [60ddc479] StatPlots v0.8.1
  [b8865327] UnicodePlots v0.3.1
  [0f1e0344] WebIO v0.4.2
  [c2297ded] ZMQ v1.0.0

Пройдёмся по прошлым руководствам

и приступим к постановке задачи

Движение заряженных частиц в электромагнитном поле

На заряженую частицу с зарядом $inline$ движущуюся в ЭМП со скоростью $inline$ действует сила Лоренца: $\vec{F}_L=q\left(\vec{E}+\left[\vec{u}\times\vec{B}\right]\right)$ . Данная формула справедлива при ряде упрощений. Пренебрегая поправками на теорию относительности, считаем массу частицы постоянной, так что уравнение движения имеет вид: $\frac{d}{dt}(m\vec{u})=q\left(\vec{E}+\left[\vec{u}\times\vec{B}\right]\right)$

Направим ось Y вдоль электрического поля, ось Z — вдоль магнитного поля и предположим для простоты, что начальная скорость частицы лежит в плоскости XY. В этом случае вся траектория частицы также будет лежать в этой плоскости. Уравнения движения примут вид:

$\left\{\begin{matrix} m\ddot{x}=qB\dot{y} \\ m\ddot{y}=qE-qB\dot{x} \end{matrix}\right.$

Обезразмерим: $x^*=\frac{x}{\lambda},\, y^*=\frac{y}{\lambda},\,\tau=\frac{ct}{\lambda},\, B^*=\frac{Bmc}{q\lambda},\, E^*=\frac{Emc^2}{q\lambda}$ . Звёздочками обозначены размерные величины, а $\lambda$ — характерный размер рассматриваемой физической системы. Получим безразмерную систему уравнений движения заряженной частицы в магнитном поле:

$\left\{\begin{matrix} \frac{d^2x}{d\tau^2}=B\frac{dy}{d\tau} \\ \frac{d^2y}{d\tau^2}=E-B\frac{dx}{d\tau} \end{matrix}\right.$

Понизим порядок:

$\left\{\begin{matrix} \frac{dx}{d\tau}=U_x \\ \frac{dy}{d\tau}=U_y \\ \frac{dU_x}{d\tau}=BU_y \\ \frac{dU_y}{d\tau}=E-BU_x \end{matrix}\right.$

В качестве начальной конфигурации модели выберем: $inline$ Тл, $E = 5\cdot 10^4$ В/м, $v_0=7\cdot 10^4$ м/с. Для численного решения воспользуемся пакетом DifferentialEquations:

Код и графики

using DifferentialEquations, Plots
pyplot()

M = 9.11e-31 # kg
q = 1.6e-19 # C
C = 3e8 # m/s
λ = 1e-3 # m

function modelsolver(Bo = 2., Eo = 5e4, vel = 7e4)

    B = Bo*q*λ / (M*C)
    E = Eo*q*λ / (M*C*C)
    vel /= C

    A = [0. 0. 1. 0.;
        0. 0. 0. 1.;
        0. 0. 0. B;
        0. 0. -B 0.]

    syst(u,p,t) = A * u + [0.; 0.; 0.; E] # ODE system

    u0 = [0.0; 0.0; vel; 0.0] # start cond-ns
    tspan = (0.0, 6pi) # time period

    prob = ODEProblem(syst, u0, tspan) # problem to solve
    sol = solve(prob, Euler(), dt = 1e-4, save_idxs = [1, 2], timeseries_steps = 1000)
end

Solut = modelsolver()

plot(Solut)

Здесь используется метод Эйлера, для которого задаётся количество шагов. Также сохраняется в матрицу ответов не всё решение системы, а только 1 и 2 индексы, то есть координаты икс и игрек (скорости нам не нужны).

X = [Solut.u[i][1] for i in eachindex(Solut.u)]
Y = [Solut.u[i][2] for i in eachindex(Solut.u)]

plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1))
title!("Траектория частицы")
yaxis!("Y")

savefig("XY1.png")#сохраним график в папку с проектом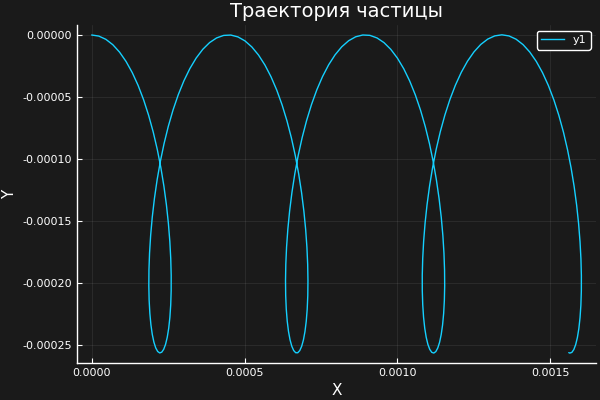

Проверим результат. Введем вместо х новую переменную $\tilde{x}=x-ut$ . Таким образом осуществляется переход в новую систему координат, движущуюся относительно исходной со скоростью u в направлении оси Х:

$\left\{\begin{matrix} \ddot{\tilde{x}}=qB\dot{y}/m \\ \ddot{y}=qE/m-qB\dot{x}/m -qBu/m \end{matrix}\right.$

Если выбрать $inline$ и обозначить $\omega=qB/m$ , то система упростится:

$\left\{\begin{matrix} \ddot{\tilde{x}}=\omega\dot{y} \\ \ddot{y}=-\omega\dot{\tilde{x}} \end{matrix}\right.$

Электрическое поле исчезло из последних равенств, и они представляют собой уравнения движения частицы, находящейся под действием однородного магнитного поля. Таким образом, частица в новой системе координат (х, у) должна двигаться по окружности. Так как эта новая система координат сама перемещается относительно исходной со скоростью $inline$ , то результирующее движение частицы будет складываться из равномерного движения по оси X и вращения по окружности в плоскости XY. Как известно, траектория, возникающая при сложении таких двух движений, в общем случае представляет собой трохоиду. В частности, если начальная скорость равна нулю, реализуется простейший случай движения такого рода — по циклоиде.
Удостоверимся, что скорость дрейфа вышла действительно равной Е/В. Для этого:

подпортим матрицу ответов, поставив вместо первого элемента (максимального) заведомо меньшее значение
найдем номер максимального элемента во втором столбце матрицы ответов, который откладывается по ординате
вычислим безразмерную скорость дрейфа, разделив значение абсциссы в максимуме на соответствующее значение времени

Y[1] = -0.1
numax = argmax( Y )
X[numax] / Solut.t[numax]

Out: 8.334546850446588e-5

B = 2*q*λ / (M*C)
E = 5e4*q*λ / (M*C*C)
E/B

Out: 8.333333333333332e-5
С точностью до седьмого порядка!
Для удобства определим функцию, принимающую параметры модели и подпись графика, которая будет также служить названием файла png, создаваемого в папке с проектом (работает в Juno/Atom и Jupyter). В отличии от Gadfly, где графики создавались в слоях, а потом выводились функцией plot(), в Plots, чтобы в одном фрейме наделать разных графиков, первый из них создается функцией plot(), а последующие добавляются использованием plot!(). Названия функций меняющих принимаемые объекты в Джулии принято оканчивать восклицательным знаком.

function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4)
    Ans = modelsolver(Bo, Eo, vel)

    X = [Ans.u[i][1] for i in eachindex(Ans.u)]
    Y = [Ans.u[i][2] for i in eachindex(Ans.u)]
    plot!(X, Y)

    p = title!(ttle)
    savefig( p, ttle * ".png" )
end

При нулевой начальной скорости, как и предполагалось, получаем циклоиду:

plot()
plotter("Zero start velocity", 2, 4e4, 7e4)

Получим траекторию частицы при занулении индукции, напряженности и при смене знака заряда. Напомню, что точка значит поочередное выполнение функции со всеми элементами массива

Упрятано

plot()
plotter.("B занулено Е варьируется", 0, [3e4 4e4 5e4 6e4] )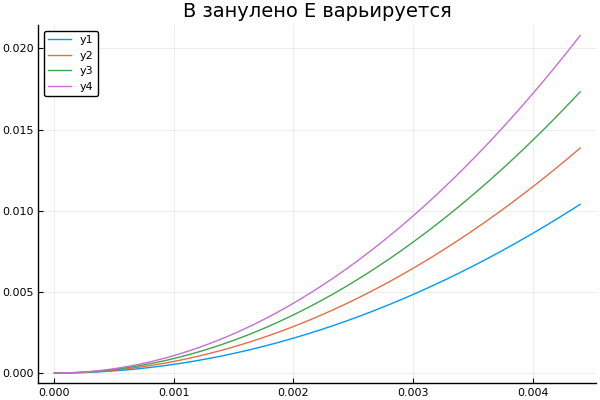

plot()
plotter.("E занулено B варьируется", [1 2 3 4], 0 )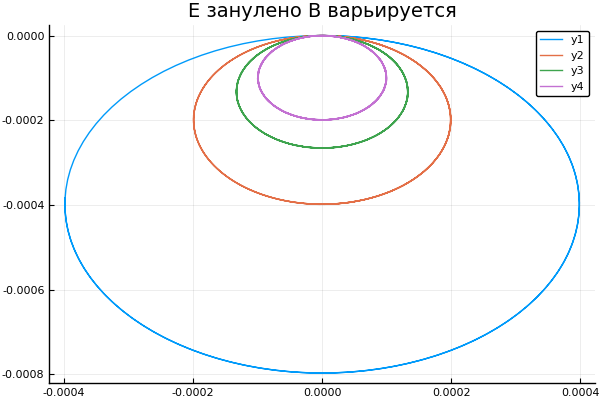

q = -1.6e-19 # C

plot()
plotter.("Отрицательный заряд")

И посмотрим, как влияет на траекторию частицы изменение начальной скорости:

plot()
plotter.("Варьирование скорости", 2, 5e4, [2e4 4e4 6e4 8e4] )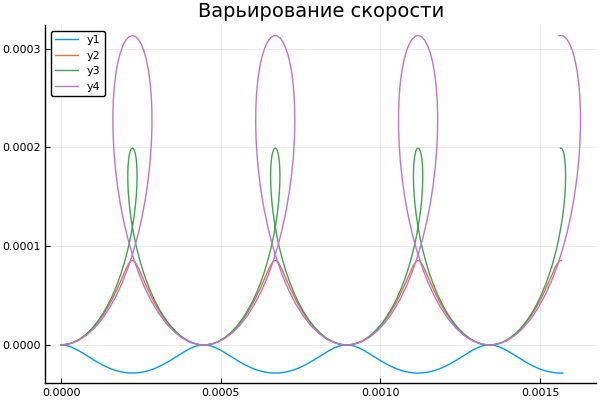

Немного о Scilab

На Хабре уже есть достаточно информации о Сайлабе, например 1, 2, а тут про Octave поэтому ограничимся ссылками на Википедию и на домашнюю страницу.

От себя добавлю, про наличие удобного создания интерфейса с флажками кнопками и выводом графиков и довольно интересного инструмента визуального моделирования Xcos. Последний можно использовать, например, для моделирования сигнала в электротехнике:

Спойлер

И здесь очень удобное руководство:

Собственно, нашу задачу вполне можно решить и в Scilab:

Код и картинки

clear

function du = syst(t, u, A, E)
    du = A * u + [0; 0; 0; E] // ODE system
endfunction 

function [tspan, U] = modelsolver(Bo, Eo, vel)

    B = Bo*q*lambda / (M*C)
    E = Eo*q*lambda / (M*C*C)
    vel = vel / C

    u0 = [0; 0; vel; 0] // start cond-ns
    t0 = 0.0
    tspan = t0:0.1:6*%pi // time period

    A = [0 0 1 0;
        0 0 0 1;
        0 0 0 B;
        0 0 -B 0]

    U = ode("rk", u0, t0, tspan, list(syst, A, E) )
endfunction 

M = 9.11e-31 // kg
q = 1.6e-19 // C
C = 3e8 // m/s
lambda = 1e-3 // m

[cron, Ans1] = modelsolver( 2, 5e4, 7e4 )

plot(cron, Ans1 )
xtitle   ("Безразмерные координаты и скорости","t","x, y, dx/dt, dy/dt");
legend   ("x", "y", "Ux", "Uy");

scf(1)//создание нового графического окна
plot(Ans1(1, :), Ans1(2, :) )
xtitle   ("Траектория частицы","x","y");

xs2png(0,'graf1');// можно сохранять графики в разных форматах
xs2jpg(1,'graf2');// правда, работает через-раз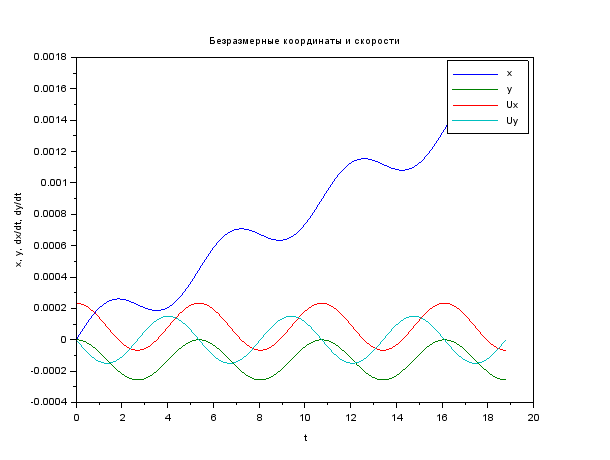

Здесь информация по функции для решения дифуров ode. В принципе напрашивается вопрос

А зачем нам Julia?

… если и так есть такие замечательные штуки как Scilab, Octave и Numpy, Scipy?
Про последние два не скажу — не пробовал. Да и вообще вопрос сложный, так что прикинем навскидку:

Scilab
На харде займет чуть больше 500 Мб, запускается быстро и сходу доступно и дифуросчитание, и графика и всё остальное. Хорош для начинающих: отличное руководство (по большей части локализованное), есть много книг на русском. Про внутренние ошибки уже было сказано тут и здесь, и так как продукт очень нишевый, сообщество вялое, и дополнительные модули весьма скудны.

Julia
По мере добавления пакетов (особенно всякой питонщины а-ля Jupyter и Mathplotlib) разрастается от 376 Мб до вполне-таки шести с лишним гигабайт. Оперативку она тоже не щадит: на старте 132 Мб и после того, как в Юпитере намалевать графиков, до 1 ГБ спокойно дойдёт. Если работать в Juno, то всё почти как в Scilab: можно выполнять код сразу в интерпретаторе, можно печатать во встроенном блокноте и сохранять как файл, есть обозреватель переменных, журнал команд и интерактивная справка. Лично у меня вызывает возмущение отсутствие clear(), т. е. запустил я код, потом начал там поправлять и переименовывать, а старые переменные-то остались (в Юпитере нет обозревателя переменных).

Но всё это не критично. Scilab подходит вполне на первых парах, сделать лабу, курсач или посчитать чего промежуточного — очень даже подручный инструмент. Хоть здесь тоже есть поддержка параллельного вычисления и вызов сишных/фортрановских функций, для чего серьезного его использовать не получается. Большие массивы повергают его в ужас, чтоб задать многомерные, приходится заниматься всяким мракобесием, а вычисления за рамками классических задач вполне могут обронить всё вместе с операционкой.

И вот после всех этих болей и разочарований можно смело переходить на Julia, чтоб огрести ещё и здесь. Будем учиться дальше, благо комьюнити очень отзывчивое, проблемы утрясаются быстро, да и у Джулии есть еще много интересных особенностей, которые превратят процесс обучения в увлекательное путешествие!

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

Julia и движение заряженной частицы в электромагнитном поле

Движение заряженных частиц в электромагнитном поле

Немного о Scilab

А зачем нам Julia?

Публикации

Истории

Ближайшие события