Привет, Хабр! Сегодня хочу поделиться небольшим примером того, как можно проводить кластерный анализ. В этом примере читатель не найдет нейронных сетей и прочих модных направлений. Данный пример может служить точкой отсчета для того, чтобы сделать небольшой и полный кластерный анализ для других данных. Всем заинтересованным — добро пожаловать под кат.
Сразу оговорюсь, эта статья ни в коем случае не претендует на академическую полноту, уникальность полученных результатов или полноту освещения вопроса. Статья призвана продемонстрировать основные шаги классического кластерного анализа, которые могут быть использованы для простого и осмысленного (возможно, предваряющего более детальное) исследования. Любые исправления, замечания и дополнения по существу приветствуются.
Данные представляют собой выборку потребления алкоголя по странам на душу населения по типу алкогольных напитков (пиво, вино, спиртные напитки и др.) за 2010 год в процентах от потребления алкоголя на душу населения. Также данные содержат: среднее суточное потребление алкоголя на душу населения в граммах чистого алкоголя и всё (зарегистрировано + неучтенное) потребление алкоголя на душу населения (только пьющие в литрах чистого алкоголя).
В то же время каждая страна условно относится к одной из географических групп: восток, центр и запад. Разделение весьма условное и очень спорное по разным причинам, но будем отталкиваться от того, что есть. Источник данных — Global status report on alcohol and health 2014, С. 289-364
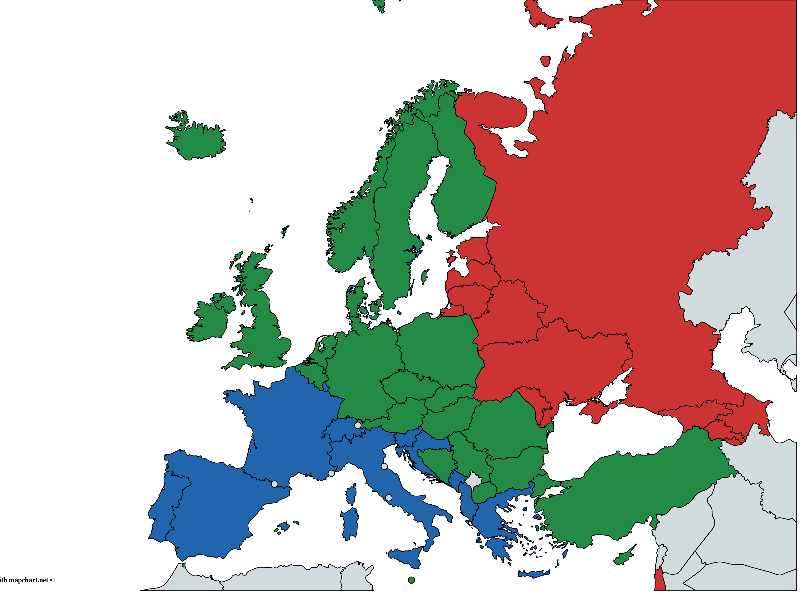
(Раскрашивал вручную, могут быть погрешности, но общая мысль, думаю, понятна)
Предварительный анализ
Подключим используемые библиотеки.
library(rgl)
library(heplots)
library(MVN)
library(klaR)
library('Morpho')
library(caret)
library(mclust)
library(ggplot2)
library(GGally)
library(plyr)
library(psych)
library(GPArotation)
library(ggpubr)Загрузим данные и посмотрим, как они выглядят.
# Загружаем данные из файла
data <- read.table("alcohol_data.csv", header=TRUE, sep=",")
# Делаем из первого столбца названия строк
rownames(data) <- make.names(data[,1], unique = TRUE)
# Записываем данные и удаляем пропуска, если они есть
data <- data[,-1]
data <- na.omit(data)
# Выводим несколько первых строчек
head(data)| Beer | Wine | Spirit | Other | Total | Average_daily | Group | |
|---|---|---|---|---|---|---|---|
| Albania | 31.8 | 19.8 | 48.4 | 0.0 | 13.0 | 27.5 | center |
| Armenia | 9.7 | 5.3 | 84.9 | 0.0 | 8.3 | 17.9 | east |
| Austria | 50.4 | 35.5 | 14.0 | 0.0 | 13.8 | 29.6 | center |
| Azerbaijan | 28.7 | 7.6 | 63.3 | 0.0 | 5.2 | 11.1 | east |
| Belarus | 17.3 | 5.2 | 46.6 | 30.9 | 22.1 | 48.0 | east |
| Belgium | 49.2 | 36.3 | 14.4 | 0.1 | 12.8 | 27.7 | center |
| ... | ... | ... | ... | ... | ... | ... | ... |
Посчитаем стандартные статистики
summary(data)
Глядя на эти статистики, можно многое сказать о характере данных. Например, что у Other очень большой разброс, и максимум сильно отстоит от третьего квартиля, значит, там есть как минимум одно сильно отличающееся наблюдение, так называемый выброс. Также видно по первому квартилю и среднему, что в этом столбце существенное количество нулевых значений, что, скорее всего, связано с недостатком данных. Также сразу видим сколько стран в каждой из групп, группы не сбалансированны по количеству. Аналогично можно рассматривать и статистики по другим признакам и делать какие-то полезные выводы и предположения.
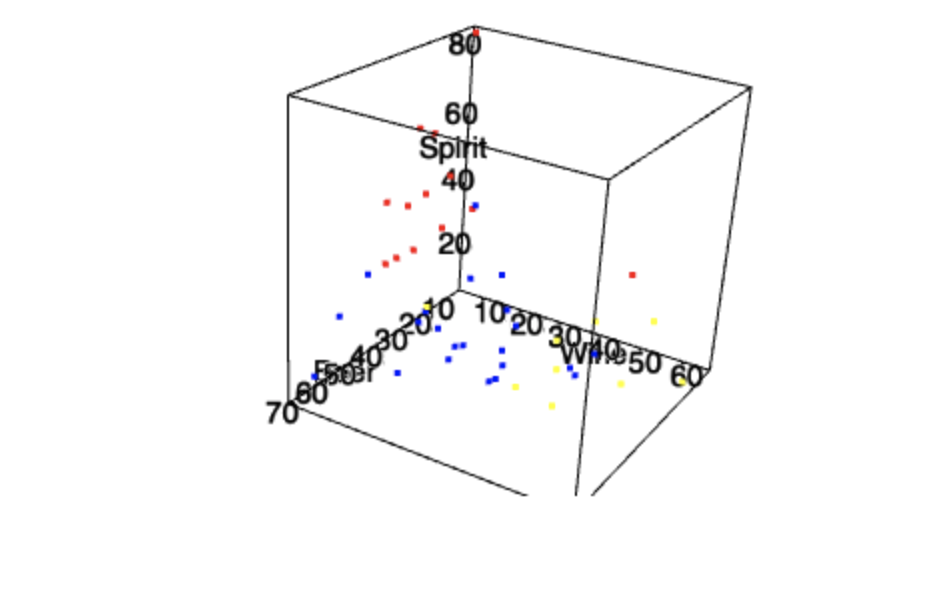
Если, как в нашем случае, у вас три основные переменные, можно попробовать отразить их на трехмерном графике.
options(rgl.useNULL=TRUE)
open3d()
mfrow3d(2,2)
levelColors <- c('west'='blue', 'east'='red', 'center'='yellow')
plot3d(data$Beer, data$Wine, data$Spirit, xlab="Beer", ylab="Wine", zlab="Spirit", col = levelColors[data$Group], size=3)
widget <- rglwidget()
widgetПолучаются довольно наглядные графики, которые можно покрутить и помасштабировать интерактивно. Судя по этому графику понятно, что по этим трем признакам группы визуально различаются.
Посмотрим эмпирические плотности по группам
ggpairs(
data,
mapping = ggplot2::aes(color = data$Group),
upper = list(continuous = wrap("cor", alpha = 0.5), combo = "box"),
lower = list(continuous = wrap("points", alpha = 0.3), combo = wrap("dot", alpha = 0.4)),
diag = list(continuous = wrap("densityDiag",alpha = 0.5)),
title = "Alcohol"
)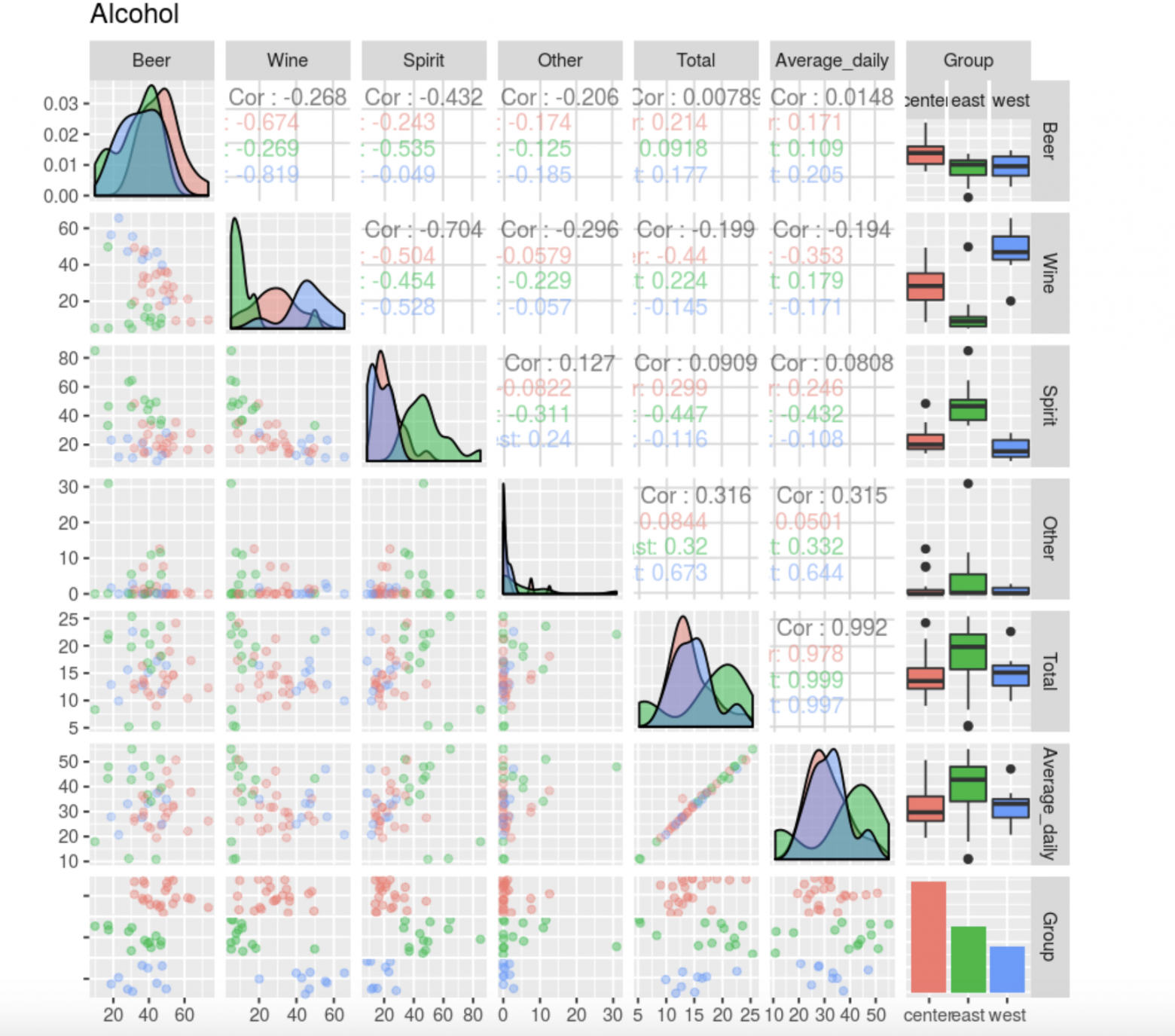
Так как Average и Total сильно коррелируют, исключим из рассмотрения Average.
data <- data[, -6]У нас несколько групп, и не только предполагается, а даже видно, что они разные, поэтому нужно рассматривать распределение отдельно по группам. Посмотрим отличающиеся данные по группам.
data[data$Wine>60,]
| Beer | Wine | Spirit | Other | Total | Group | |
|---|---|---|---|---|---|---|
| Italy | 23 | 65.6 | 11.5 | 0 | 9.9 | west |
В том что итальянцы пьют вина больше всех, даже без учета разделения на группы, думаю, нет ничего удивительного, поэтому из-за того, что и так мало данных, оставим это наблюдение.
data[data$Spirit>70,]
data[data$Spirit<10,]| Beer | Wine | Spirit | Other | Total | Group | |
|---|---|---|---|---|---|---|
| Armenia | 9.7 | 5.3 | 84.9 | 0 | 8.3 | east |
| Beer | Wine | Spirit | Other | Total | Group | |
|---|---|---|---|---|---|---|
| Slovenia | 44.5 | 46.9 | 8.6 | 0 | 17.2 | west |
Весьма подозрительные данные относительно выборки, пока оставим их, но будем иметь в виду.
Данных не так много, поэтому посмотрим на данные по группам
split(data[,1:5],data$Group)$center
| Beer | Wine | Spirit | Other | Total | |
|---|---|---|---|---|---|
| Albania | 31.8 | 19.8 | 48.4 | 0.0 | 13.0 |
| Austria | 50.4 | 35.5 | 14.0 | 0.0 | 13.8 |
| Belgium | 49.2 | 36.3 | 14.4 | 0.1 | 12.8 |
| Bosnia.and.Herzegovina | 73.3 | 9.7 | 17.0 | 0.0 | 12.3 |
| Cyprus | 40.9 | 24.7 | 33.7 | 0.7 | 10.8 |
| Czech.Republic | 53.5 | 20.5 | 26.0 | 0.0 | 14.6 |
| Denmark | 37.7 | 48.2 | 14.1 | 0.0 | 12.9 |
| Finland | 46.0 | 17.5 | 24.0 | 12.6 | 18.1 |
| Germany | 53.6 | 27.8 | 18.6 | 0.0 | 14.7 |
| Hungary | 36.3 | 29.4 | 34.3 | 0.0 | 16.3 |
| Iceland | 61.8 | 21.2 | 16.5 | 0.5 | 10.4 |
| Ireland | 48.1 | 26.1 | 18.7 | 7.7 | 14.7 |
| Malta | 39.4 | 32.7 | 27.2 | 0.7 | 11.5 |
| Netherlands | 46.8 | 36.4 | 16.9 | 0.0 | 11.2 |
| Norway | 44.2 | 34.7 | 19.0 | 2.1 | 9.0 |
| Poland | 55.1 | 9.3 | 35.5 | 0.0 | 24.2 |
| Romania | 50.0 | 28.9 | 21.1 | 0.0 | 21.3 |
| Serbia | 51.5 | 23.9 | 24.6 | 0.0 | 19.0 |
| Sweden | 37.0 | 46.6 | 15.1 | 1.4 | 13.3 |
| Switzerland | 31.8 | 49.4 | 17.6 | 1.2 | 12.1 |
| Turkey | 63.6 | 8.6 | 27.9 | 0.0 | 17.3 |
| UK | 36.9 | 33.8 | 21.8 | 7.5 | 13.8 |
$east
| Beer | Wine | Spirit | Other | Total | |
|---|---|---|---|---|---|
| Armenia | 9.7 | 5.3 | 84.9 | 0.0 | 8.3 |
| Azerbaijan | 28.7 | 7.6 | 63.3 | 0.0 | 5.2 |
| Belarus | 17.3 | 5.2 | 46.6 | 30.9 | 22.1 |
| Bulgaria | 39.3 | 16.5 | 44.1 | 0.1 | 16.9 |
| Estonia | 41.2 | 11.1 | 36.8 | 10.9 | 15.7 |
| Georgia | 17.0 | 49.8 | 33.2 | 0.1 | 21.2 |
| Israel | 44.0 | 6.2 | 49.5 | 0.3 | 5.4 |
| Latvia | 46.9 | 10.7 | 37.0 | 5.4 | 18.1 |
| Lithuania | 46.5 | 7.8 | 34.1 | 11.6 | 23.6 |
| Republic.of.Moldova | 30.4 | 5.1 | 64.5 | 0.0 | 25.4 |
| Russian.Federation | 37.6 | 11.4 | 51.0 | 0.0 | 22.3 |
| Slovakia | 30.1 | 18.3 | 46.2 | 5.5 | 19.8 |
| Ukraine | 40.5 | 9.0 | 48.0 | 2.6 | 20.3 |
$west
| Beer | Wine | Spirit | Other | Total | |
|---|---|---|---|---|---|
| Croatia | 39.5 | 44.8 | 15.4 | 0.2 | 15.1 |
| France | 18.8 | 56.4 | 23.1 | 1.7 | 12.9 |
| Greece | 28.1 | 47.3 | 24.2 | 0.4 | 15.6 |
| Italy | 23.0 | 65.6 | 11.5 | 0.0 | 9.9 |
| Luxembourg | 36.2 | 42.8 | 21.0 | 0.0 | 12.7 |
| Portugal | 30.8 | 55.5 | 10.9 | 2.8 | 22.6 |
| Slovenia | 44.5 | 46.9 | 8.6 | 0.0 | 17.2 |
| Spain | 49.7 | 20.1 | 28.2 | 1.8 | 16.4 |
| Republic.of.Macedonia | 47.4 | 39.9 | 12.6 | 0.0 | 11.7 |
ggpairs(
data,
mapping = ggplot2::aes(color = data$Group),
diag=list(continuous="bar", alpha=0.4)
)
Из гистограмм видно, что группы лучше всего различаются по пиву, вину и спиртным напиткам. Если брать признак Other, заметим: мало того, что у него весьма странное распределение, так еще и в большинстве стран маленькие и даже нулевые значения, кроме нескольких (примерно 10-12 стран, а так как индивидов всего 45, исключив их, мы существенно сократим объем данных). Больше всего отличается Республика Беларусь. Немного подумав, можно сделать предположение, что там предпочитают крамбамбуля вместо пива, вина и спиртных напитков (шутка). Ну, а если более формально, то скорее всего это связано с неполнотой исходных данных или несовершенством регистрации данных. Уберем признак Other из рассмотрения.
Также на гистограммах можно заметить, что для центра превалирует пиво, для запада — вино, а для востока — спиртные напитки. Это вполне укладывается в общеизвестные представления, можно даже сказать — стереотипы, о культуре потребления спиртных напитков в этих регионах.
На диаграммах рассеяния признака Total и Other, визуально группы не выделяются. Будем иметь этот факт в виду в дальнейшем.
Примечательно, что между признаками Beer, Spirit и Wine отрицательные корреляции. Возможно, это также относится к тому, что по этим переменным можно выделять группы предпочтения в алкоголе, и они будут близки к географическим. После того как изучили данные, получили некие априорные представления, убрали лишние, на наш взгляд, признаки, перейдем к кластерному анализу.
Кластерный анализ
Уберем разметку данных на группы и уберем признак Total. Это позволит не нормировать данные, так как остальные признаки — в одной шкале.
data.group = data[,5]
data <- data[,-5]
data<- data[,-4]Определим число кластеров Elbow method (“метод согнутого колена”, он же “метод каменистой осыпи”). Построим график, где по оси абсцисс отмечено число кластеров k, а по оси ординат – значения функции W(K), которая определяет внутригрупповой разброс в зависимости от числа кластеров.
library(factoextra)
fviz_nbclust(data, kmeans, method = "wss") +
labs(subtitle = "Elbow method") +
geom_vline(xintercept = 4, linetype = 2)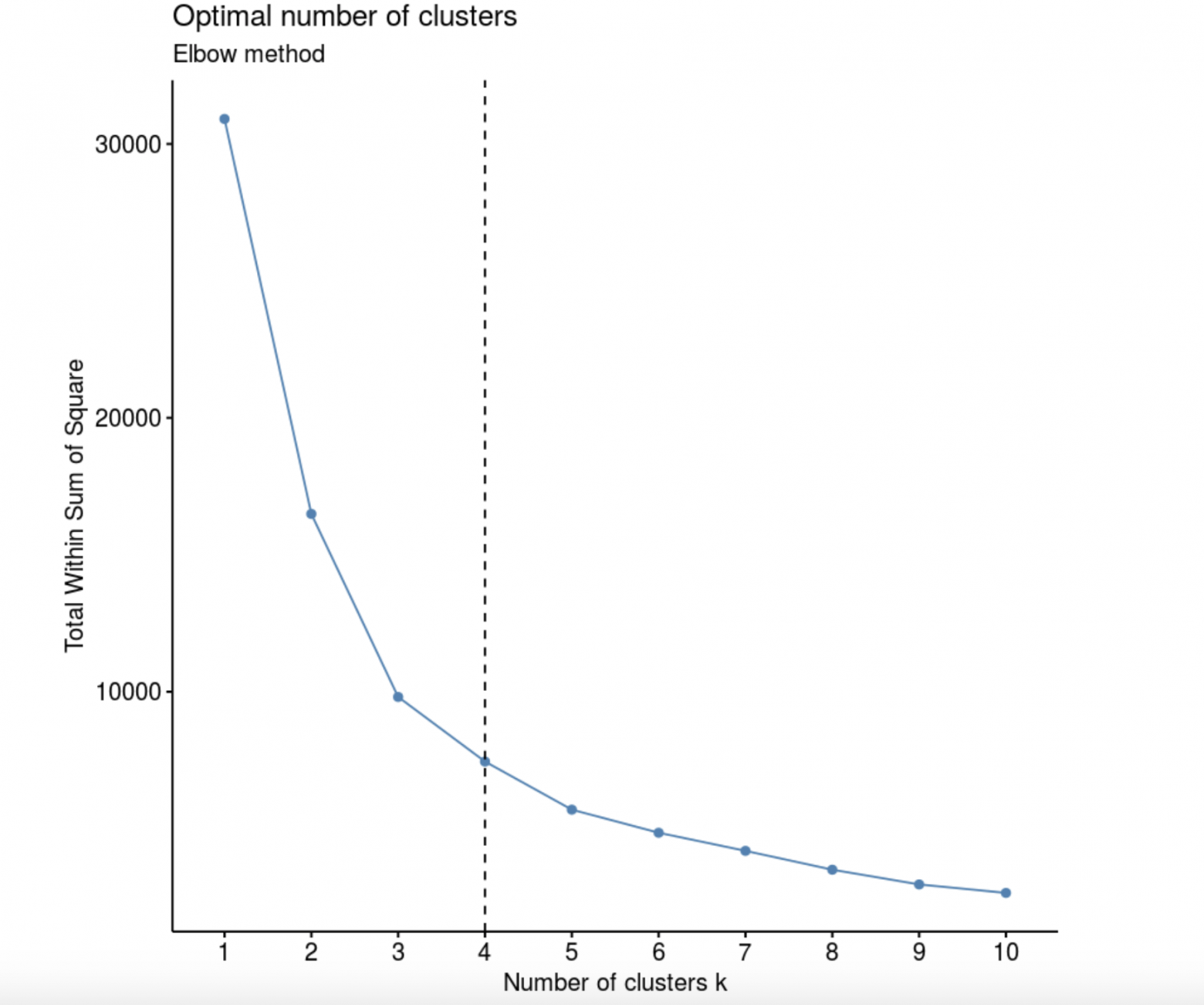
data.dist <- dist((data))
hc <- hclust(data.dist, method = "ward.D2")
plot(hc, cex = 0.7)
Нарисуем график поинтереснее. Цвета будут означать исходную географическую маркировку.
colors=c('green', 'red', 'blue')
hcd = as.dendrogram(hc)
clusMember = cutree(hc, 4)
colLab <- function(n) {
if (is.leaf(n)) {
a <- attributes(n)
labCol <- colors[data.group[n]]
attr(n, "nodePar") <- c(a$nodePar, lab.col = labCol)
}
n
}
clusDendro = dendrapply(hcd, colLab)
plot(clusDendro, main = "Cool Dendrogram", type = "triangle")
rect.hclust(hc, k = 4)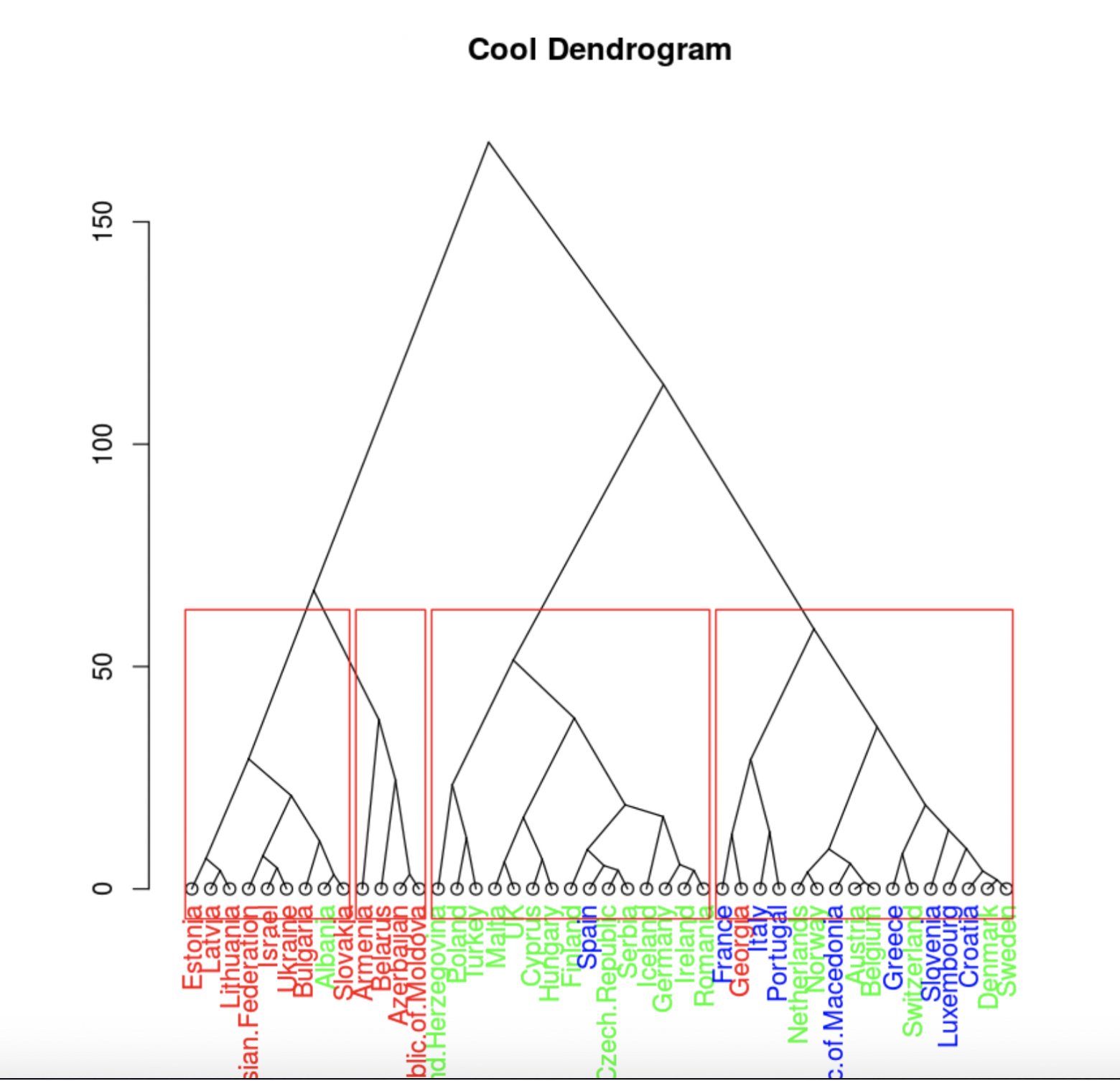
Грузия из восточного кластера единственная не попала в свой географический кластер. Пока отложим интерпретацию, посмотрим на другие методы.
Причем здесь, наверное, лучше использо��ать три кластера, так как в четвертый кластер странно выделились всего 4 страны.
plot(clusDendro, main = "Cool Dendrogram", type = "triangle")
data.hclas_group <- factor(cutree(hc, k = 3))
rect.hclust(hc, k = 3)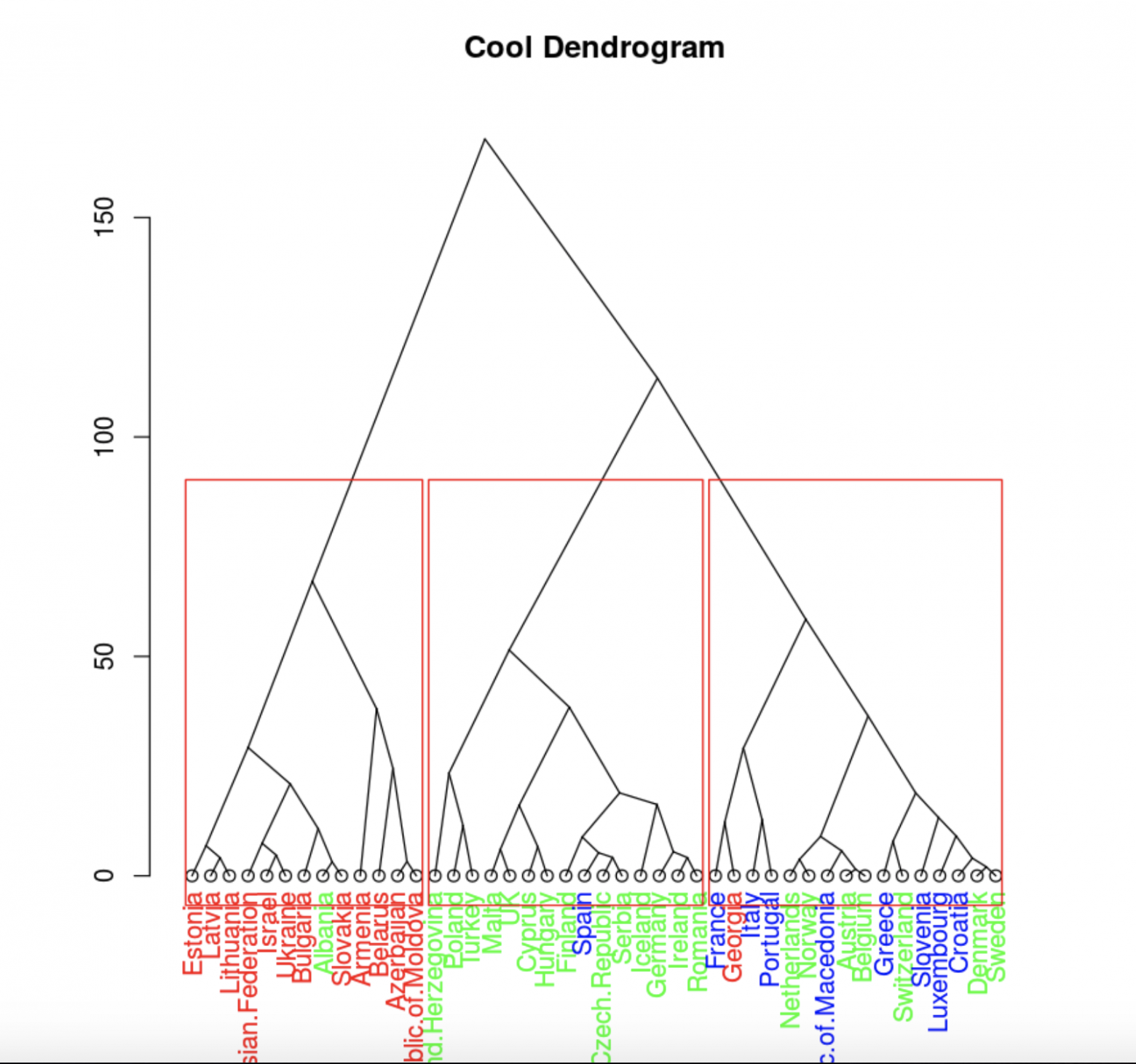
Конечно, если мы хотим увидеть информативный график в двух измерениях, нужно использовать первые две главные компоненты.
library(FactoMineR)
res.pca <- PCA(data,scale.unit=T, graph = F)
fviz_pca_biplot(res.pca,
col = colors[data.hclas_group], palette = "jco",
label = "var",
ellipse.level = 0.8,
addEllipses = T,
col.var = "black",
legend.title = "groups4")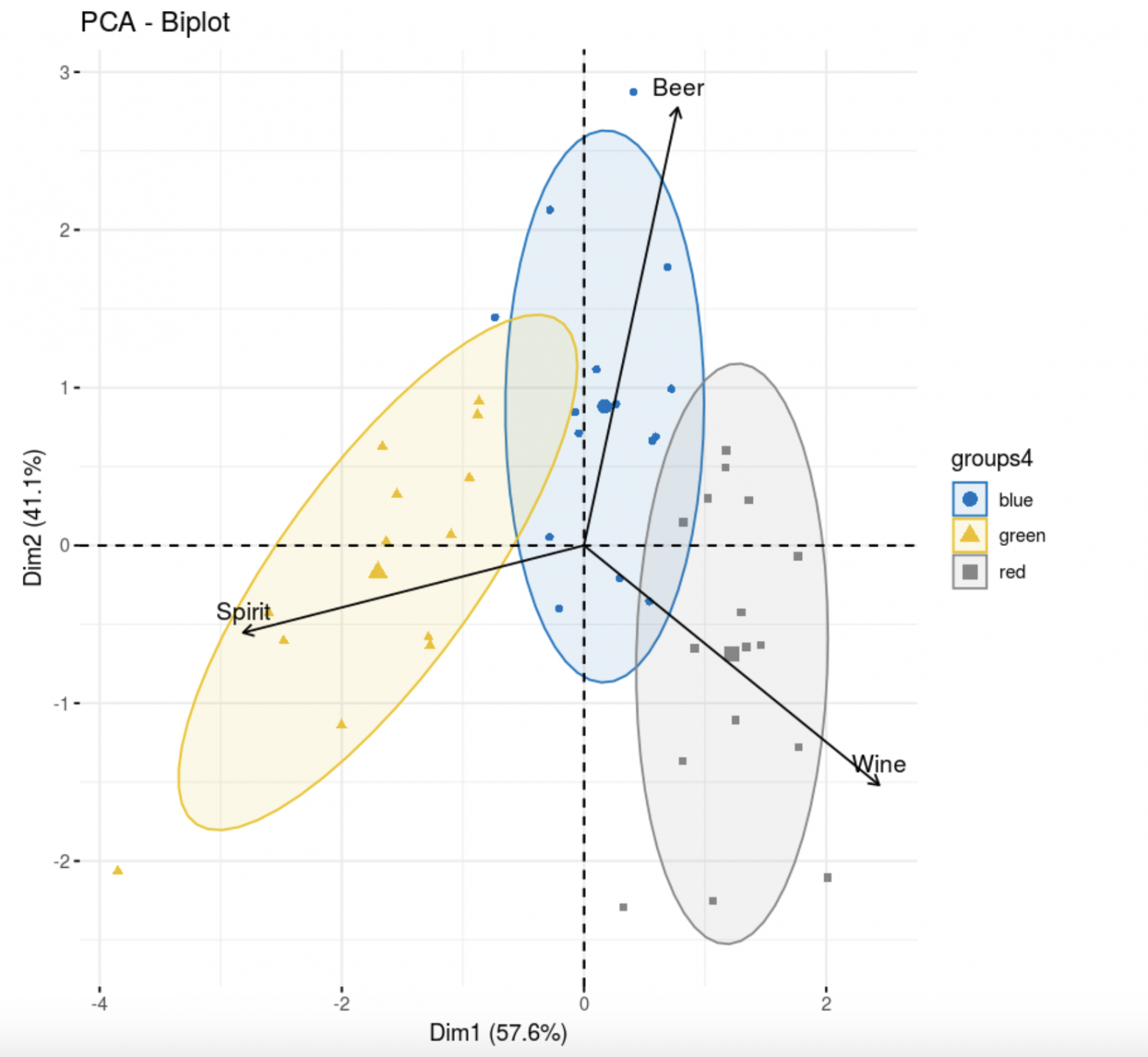
Третья группа, которая по центру, портит всю картину. Если бы она была покучнее, можно было говорить о кластеризации, а так это, скорее, сегментация. В целом, между группами заметно различие, посмотрим, как справится метод k-средних++.
library(flexclust)
data.kk <- kcca(data, k=3, family=kccaFamily("kmeans"),
control=list(initcent="kmeanspp"))
fviz_pca_biplot(res.pca,
col.ind =as.factor(data.kk@cluster), palette = "jco",
label = "var",
ellipse.level = 0.8,
addEllipses = T,
col.var = "black", repel = TRUE,
legend.title = "clusters")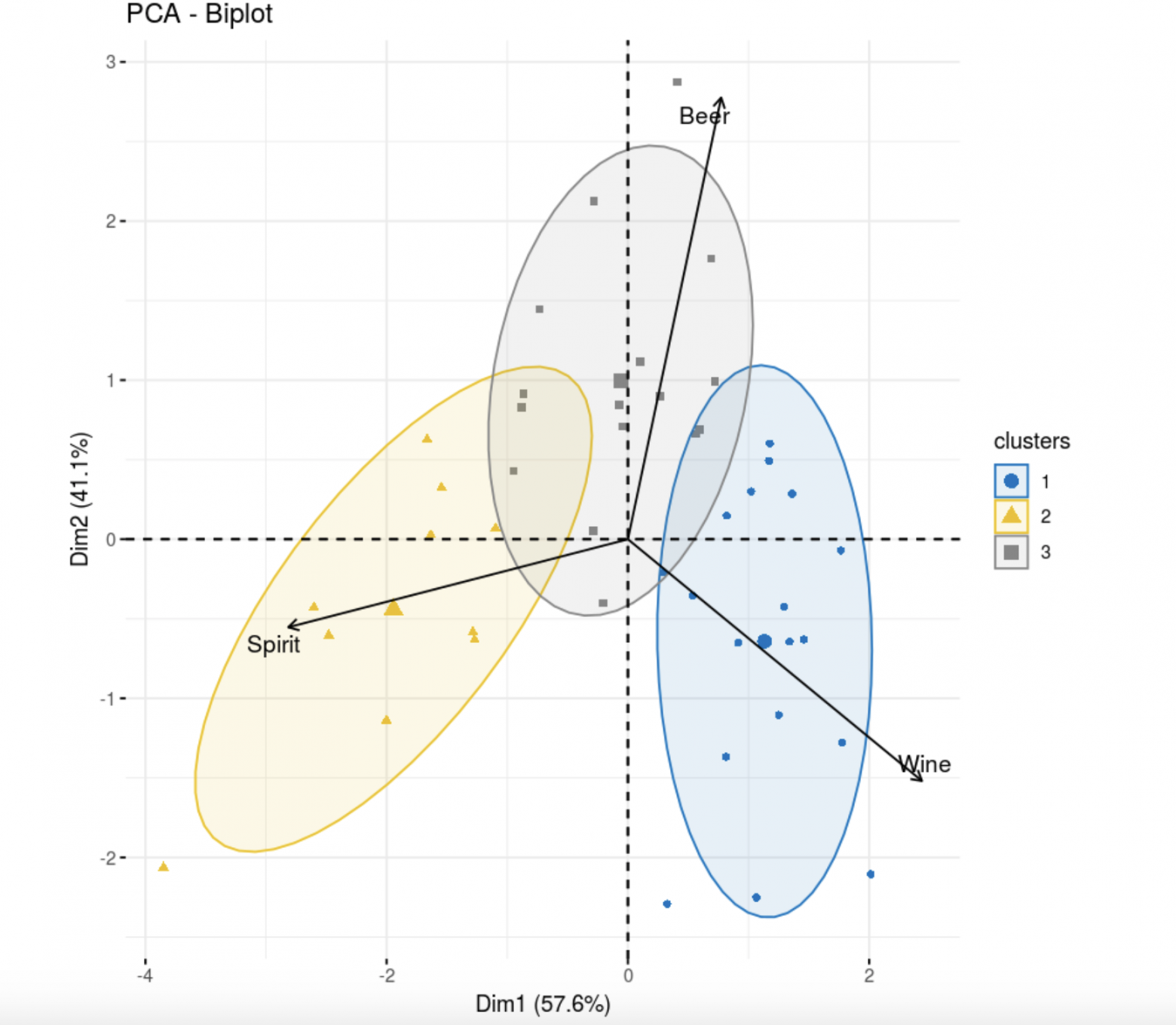
Эллипсоид третьей группы получился слишком широким, так как k-средних пытается разбить на равные кластеры. Из графика видно, что метод включил в третий кластер лишние точки, которые скорее должны относиться к другим кластерам.
Больше всего, исходя из исходных классов, на правду похож hclust. Проинтерпретируем результат.

Наиболее полный кластер, в смысле исходной классификации, образовали восточные страны. К ним попала Албания из центральной части. Стоит отметить, что Албания пространственно находится недалеко от восточных стран.
Второй кластер также очень похож на исходное разделение. В третьем же все плохо. В исходной выборке там меньше всего индивидов, и они очень близки по предпочтениям в алкоголе, согласно данным, к центральной части. Можно попробовать условно разделить на два кластера, так как видно, что для интерпретации лучше всего так и сделать и резюмировать биполярность Европы. Тогда кластера практически совпадут с Восточной и Западной Европой, где в Западную войдет центральная и Западная по исходным обозначениям.
Можно было бы провести кластеризацию на основе предположения о моделях кластеров, используя информационные критерии (тут описание), а также попробовать классический дискриминантный анализ для этого набора данных. Если эта статья была полезной, то планирую опубликовать продолжение.
