OpenCASCADE и Невидимое солнце Дао / Хабр

Тот лучший путник, что следов не оставляет
Тот лучший лидер, что без речи вдохновляет
План совершенен, если плана вовсе нет
И если мудрый двери закрывает,
Вам никогда не разгадать секрет.

Великая книга Дао - Стих 27 ( Перевод Ю. Полежаевой)

Привет, Хабр! Хочу сегодня пригласить в увлекательное 3D-путешествие. Мне нравится 3D. И хотя я пробовал работать в разных программах, но меня не покидало чувство, что мне чего-то не хватает. Даже если пользоваться встроенным скриптингом.

Поэтому я постепенно пришел к идее, что для реализации моих безумных творческих идей, наверное лучше подойдут CAD-системы. Вот там есть где разгуляться 3D-фантазии. Мощные алгоритмы создания поверхностей пересечений, проекций, аппроксимаций. Это как раз то, что нужно. Вообще, мне кажется, что разработчики промышленных геометрических CAD-ядер относятся к остальному 3D миру по принципу "Солдат ребенка не обидит".

Конечно, в своих поисках я не мог пройти мимо открытого CAD-ядра OpenCascade. Эта библиотека предоставляет уникальную возможность ближе познакомится с принципами внутреннего устройства современных CAD-систем. Вдвойне приятно, что это можно сделать на дружелюбном языке Python.

От одной мысли о всех этих чудесах, мое сердце начинает биться сильнее. Как поется в одной песне - я приятную дрожь ощущаю с головы до ног. Тех у кого в этот вечер похожее настроение - прошу под кат. Будем рисовать Инь и Янь в объеме.

Главное - поставить сильную задачу

Для того, чтобы испытать CAD-ядро, я решил нарисовать в объеме символ Дао. Какой практический смысл в рисовании древнего китайского символа? Да практически никакого, кроме того, что в процессе рисования потребуются нетривиальные операции и мы сможем проверить, насколько ядро устойчиво ко всяким творческим 3D-махинациям.

Мне в этом смысле понравилась идея, которую я услышал по телевизору от одного астронома. Ведущий его спросил: "Какой практический смысл имеется в астрономии для экономики и народного хозяйства?" Любой ученый от подобных вопросов может легко впасть в депрессию. Но в данном случае астроном не растерялся и ответил, что главный смысл астрономии для народного хозяйства в том, что она ставит перед инженерами по настоящему сильные задачи. Благодаря этому появились сверхчувствительные приемники, сверхточная обработка поверхностей, и много еще чего сверх.

Задача поставлена. И все на что мы можем надеяться - это на древние силы даосизма и на современные силы 3D-моделирования. Как гласит древняя китайская мудрость даже самый далекий и сложный путь начинается с первого шага.

Шаг 1. Настройка среды

Приведу ссылку на разработанный мною документ по настройке OpenCascade в среде Анаконда. Инструкция расcчитана на Win64. Но я думаю, что на Linux можно настроить, не намного сложнее, а может даже и проще.

Установка OpenCascade - Python 3.7 - Win64

Здесь же я оставлю еще несколько ссылок, которые помогут ближе познакомится с OpenCascade

Официальный сайт OpenCascade
Документация
Человек, который занимается OpenCascade for Python (очень крутой товарищ)

При запуске команд, conda (пакетный менеджер Анаконды) будет пыхтеть и ворчать, считать и пересчитывать зависимости. Когда же он завершит свою нелегкую работу и все нормально запустится, будет ощущение что вам крупно повезло. Возможно так оно и есть.

Шаг 2. Небольшая самодельная библиотека

Чтобы не загромождать код ненужными деталями я написал небольшой набор функций. Ничего выдающегося в нем нет, но я приведу описание этих функций, чтобы было понятно что происходит в примерах.

#initMode = 'screen','web','stl'
def ScInit(initMode, decoration, precision, exportDir):
  pass

#default styles
#'stInfo' - for service objects
#'stMain' - for main object of drawing
#'stFocus' - for important details
def ScStyle(styleVal):
  pass

#draw objects
def ScPoint(pnt, style):
  pass
def ScLine(pnt1, pnt2, style):
  pass
def ScCircle(pnt1, pnt2, pnt3, style):
  pass
def ScShape(shape, style):
  pass
def ScLabel(pnt, text, style):
  pass

#start render
def ScStart()

К слову сказать, в библиотеке PythonOCC, кроме непосредственно интерфейса к функциям ядра OpenCascade (cгенерированного с помощью SWIG) понаписано еще много всякого Python-кода, сильно облегчающего жизнь, и за это хочется сказать спасибо тем, кто это сделал.

Шаг 3. Немного о структуре OpenCASCADE

Библиотека OpenCascade неплохо структурирована - в ней все разнесено по уровням. Вначале это кажется излишним, но потом понимаешь, что это разделение вполне логично и полезно. Я бы выделил четыре основных уровня. Чтобы на экране что-то появилось нужно пройти все эти уровни. К счастью, переходы между уровнями довольно легко организованы с помощью различных конструкторов и деструкторов

Математический уровень (линейная алгебра) - точки, вектора, направления, оси, преобразования. Названия пакетов начинаются с gp (что это значит я так и не понял - может geometry primitives)
Геометрический уровень - здесь мы сталкиваемся с различными двухмерными и трехмерными кривыми и поверхностями, задаваемыми различными способами. Названия пакетов начинаются с Geom
Топологический (структурный уровень) - на этом уровне из геометрических объектов, как лоскутное одеяло, сшиваются рабочие объекты. Основные понятия - вершина (vertex), ребро(edge) отрезок кривой или прямой, соединяющий две вершины, контур (wire) - замкнутый набор из ребер, грань (face) - поверхность ограниченная контуром, оболочка (shell) - замкнутый набор граней, ограничивающий некоторый объем, тело (solid) - непосредственно сам объем, ограниченный оболочкой. Согласитесь, что разделение понятий оболочки и тела - граничит с деструктивным педантизмом и во многих 3D-приложениях данное различие просто не принимается во внимание. Здесь же все разложено по полочкам. Топологический уровень - основное отличие библиотек, основанных на граничном представлении объектов (boundary representation), поэтому пакеты данного уровня начинаются с префикса BRep и Topo
Уровень отображения - здесь мы конструируем объекты, которые непосредственно появляются на экране и взаимодействуют с пользователем. Геометрические формы обретают цвет, материал, положение в пространстве, могут быть выбраны мышкой и вообще ведут себя с пользователем очень дружелюбно, за что им был дан префикс AIS).

Еще хотелось бы поделится некоторыми наблюдениями, которые могут вам помочь в работе.

Имя каждого объекта имеет префикс, совпадающий с именем пакета в котором он находится. Это железная необходимость, которая позволяет создателям библиотеки самим не запутаться во всем этом зоопарке. Поэтому при импорте в Python смело пишите в качестве пакета префикс объекта - вы никогда не ошибетесь. Кроме того, зная префикс, можно посмотреть, какие объекты еще есть в пакете. Возможно они подойдут для ваших целей больше, чем тот объект, который вы увидели в примере.
Создатели OpenCascade в плане придумывания имен и сокращений обладают буйной фантазией и имена объектов OpenCascade не пересекаются с именами никаких других библиотек. Поэтому если вы хотите получить справку по объекту - смело вводите его имя в Google. Ссылка на документацию на этот объект окажется в первой строчке выдачи.
Имена и методы объектов не изменяются в зависимости от языка на котором происходит общение с OpenCascade, поэтому вы легко можете использовать примеры и на родном для библиотеки C++, и на ставшем уже экзотикой Tcl, также можно встретить примеры на Java. При должных навыках компьютерного полиглотства все эти примеры легко транслируются в Python.
При использовании объектов будьте внимательны, педантичны и действуйте аккуратно. Очень часто имена объектов и методов отличаются всего на одну букву, а результат их работы отличается кардинально. Я так обжигался несколько раз, и только удача спасала мое психическое здоровье.

Теперь можно приступать к рисованию. Начнем с классики.

Шаг 4. Классические формы Инь и Янь.

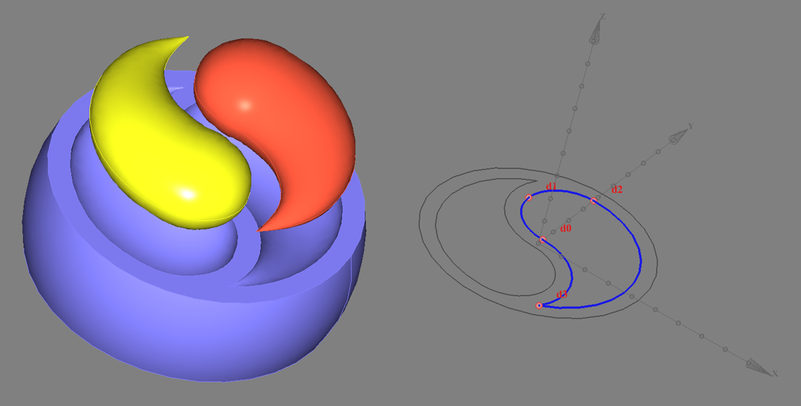
Будем использовать принципы параметрического моделирования и единственный параметр который нам потребуется - это r - базовый радиус даосского символа. Как известно символ состоит из большой дуги и двух малых дуг. Я разобью малую дугу головы символа на две дуги. Я это делаю, потому что хочу чтобы в топологии присутствовала точка - вершина символа. Она нам в дальнейшем сильно поможет в построениях.

Первое, что мы сделаем - наметим базовые точки, на которых будет построен нужный нам контур. Базовые точки включают в себя вершины дуг, а также центральные точки для каждой дуги. Построение дуги по трем точкам - это самый удобный способ построения дуги как на плоскости, так и в пространстве. Поверьте мне на слово - если вы задумайте построить дугу каким-то другим способом вы надолго выпадите из культурной, рабочей и семейной жизни.

Вот что получилось (обращаю внимание здесь и далее - это не полный код, а важные для шага процедуры, ссылка на полный код в конце поста):

def getPntsBase(r):
    
    r2 = r/2
    
    gpPntMinC = gp_Pnt(0,r2,0)
    
    p0 = gp_Pnt(0,0,0)      
    p1 = getPntRotate(gpPntMinC , p0, -pi/4)      
    p2 = gp_Pnt(-r2,r2,0)      
    p3 = getPntRotate(gpPntMinC , p0, -pi/4*3)      
    p4 = gp_Pnt(0,r,0)      
    p5 = gp_Pnt(r,0,0)      
    p6 = gp_Pnt(0,-r,0)      
    p7 = gp_Pnt(r2,-r2,0)      
    
    return p0, p1, p2, p3, p4, p5, p6, p7
  
def getWireDaoClassic(ppBase):
    
    p0, p1, p2, p3, p4, p5, p6, p7  = ppBase
    
    arc1 =  GC_MakeArcOfCircle(p0,p1,p2).Value()
    arc2 =  GC_MakeArcOfCircle(p2,p3,p4).Value()
    arc3 =  GC_MakeArcOfCircle(p4,p5,p6).Value()
    arc4 =  GC_MakeArcOfCircle(p6,p7,p0).Value()
 
    edge1 = BRepBuilderAPI_MakeEdge(arc1).Edge()
    edge2 = BRepBuilderAPI_MakeEdge(arc2).Edge()
    edge3 = BRepBuilderAPI_MakeEdge(arc3).Edge()
    edge4 = BRepBuilderAPI_MakeEdge(arc4).Edge()
  
    shape =  BRepBuilderAPI_MakeWire(edge1, edge2, edge3, edge4).Wire()
    
    return shape
 
def slide_01_DaoClassic(r):
    
    drawCircle(r, 'stInfo')
    pntsBase = getPntsBase(r)
    drawPoints(pntsBase, 'stFocus', 'b')
    shapeDaoClassic = getWireDaoClassic(pntsBase)
    ScShape(shapeDaoClassic, 'stMain')

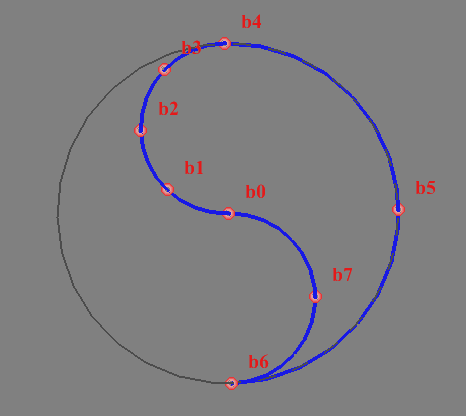
Прикладываю ссылку на WebGL-презентацию: Слайд 01 Контур классического Дао

Здесь вы можете посмотреть этот чертеж в объеме. Если у вас есть 3D-телевизор или 3D-проектор то возможен просмотр в стерео-режиме. Просто нажмите иконку 3D - 1 раз - перекрестный взгляд - 2 раза - режим SideBySide.

В завершение этого этапа хочу немного поразмышлять - это у меня такая беда - размышлять по самым пустяковым поводам.

Если вы задумайте определять координаты точек и расстояния, с помощью теоремы Пифагора и тригонометрических знаний, полученных в 6-ом классе, то это конечно сработает, но настоящие CAD-индейцы так не поступают. Все что вам нужно в плане нахождения координат, углов, расстояний и направлений делается с помощью векторной алгебры без привлечения каких-либо других допотопных методов. Создатели 3D-библиотек очень расстроятся, если вы вдруг для поворотов в пространстве не будете использовать квартернионы, которые они так заботливо реализовали специально, чтобы облегчить вам жизнь.

Не вздумайте задавать углы в градусах и писать функции типа DegreeToRadian. Импортируйте константу pi и задавайте углы поворота только как pi, pi/4, -pi/8 и так далее. Если кто-то из ваших знакомых прознает, что вы все еще мыслите в градусах, о вас поползет дурная слава. В мире математики вы станете изгоем и даже выпускники 9-ых классов никогда не подадут вам руки. Чтобы как-то обосновать эту мысль, скажу, что вся тригонометрия вычисляется на компьютере при помощи рядов и значение в радианах сразу можно подставить в ряд без каких-либо преобразований. В общем, давайте беречь ресурсы наших компьютеров.

На самом деле вопрос не столь очевиден. Так когда мне в 8 классе сказали, что теперь начинается другая жизнь и отныне мы будем измерять углы в естественных единицах - радианах, я очень удивился. Ничего естественного в том, чтобы задавать углы иррациональными числами я не увидел. Наиболее естественным мне представлялась измерять углы а оборотах - 1 - 1 оборот, 2 - 2 оборота. Конечно я тогда был наивен и не знал про ряды, пределы, гармонический анализ , и про то что вся математическая кухня намного упрощается если исходить из радианов.

Здесь уже можно перейти к следующему шагу и попробовать немного улучшить, то что придумали китайцы шесть тысяч лет назад.

Шаг 5. Улучшаем совершенство

Давайте сделаем так, чтобы между нашими Инь и Янь был некоторый отступ. Так мы подготовим базу для объемных построений. Согласитесь, если объемные тела будут соприкасаться это будет не очень красиво.

Здесь м�� проведем первое испытание библиотеки на математическую прочность. Используем функцию отступа. Она называется Offset. Для этого нам понадобится еще один параметр - размер отступа.

def getShapeOffset(shape, offset):
    tool = BRepOffsetAPI_MakeOffset()
    tool.AddWire(shape)
    tool.Perform(offset)
    shape = tool.Shape()  
    return shape

def slide_02_DaoConcept(r, offset):
    
    drawCircle(r + offset, 'stInfo')
    pntsBase = getPntsBase(r)
    wireDaoClassic = getWireDaoClassic(pntsBase)
    wireDao0 = getShapeOffset(wireDaoClassic, -offset)
    ScShape(wireDao0, 'stMain')
  
    pntsDao0 = getPntsOfShape(wireDao0)
    drawPoints(pntsDao0, 'stFocus', 'd')
  
    wireDao1 = getShapeOZRotate(wireDao0, pi)
    ScShape(wireDao1, 'stInfo')

Ссылка на WebGL-презентацию: Слайд 02 Контур Дао с отступом

Ура, получилось. Обратите внимание, как бережно библиотека обошлась с топологией. Количество точек было сохранено и они оказались именно там где нужно. Я считаю это большое достижение для создателей библиотеки. Настало время для серьезных дел - выходим в 3D.

Шаг 6. Строим сечение. Заметки о самом главном.

Как задать форму объемного тела? Один из методов заключается в том, чтобы задать сечения объекта. Причем если нам удастся сделать это непрерывным образом - считайте дело в шляпе. С точки зрения математики наша задача решена. Кому-то этот шаг может показаться невзрачным, но именно он является САМЫМ ГЛАВНЫМ с точки зрения построения объекта.

Если мы внимательно посмотрим на наш об��ект, то с геометрической точки зрения мы отчетливо можем выделить две составляющие - голову круглой формы и хвост, форма которого вообще не имеет определенного названия. Сечения для головы и хвоста должны строится по-разному.

Голову мы будем рассекать параллельными прямыми. Понятно, что в результате получится полусфера, но чтобы сохранить общий подход мы все-таки построим ее с помощью сечений. Сечения же для хвоста будем проецировать из некоего фокуса. Где должен быть этот фокус? Фокус должен находится в точке, откуда все сечения будут максимально условно перпендикулярны к объекту. Путем подбора я определил, что наилучшие результаты получаются когда фокус находится на оси Y на расстоянии -r/4 от центра.

Сечение будем задавать с помощью параметра k. При к = 0 мы находимся в начале нашей фигуры. При k = 1 в конце. Во всех промежуточных значениях алгоритм должен строить сечение объекта. Что касается самого сечения - предположим что это окружность (раз уж здесь везде окружности)

def getPntDaoFocus(r):
    return gp_Pnt(0,-r/4,0)


def getPntsForDaoSec(pntDaoStart, pntUpLimit, pntDaoEnd, pntDownLimit, pntFocus, k):
    angleLimit = 0
    pntLimit = getPntScale(pntFocus, pntUpLimit, 1.2)
    angleStart = getAngle(pntFocus, pntLimit, pntDaoStart)
    angleEnd = getAngle(pntFocus, pntLimit, pntDaoEnd)
    kLimit = (angleLimit - angleStart)/(angleEnd - angleStart)
    if k < kLimit: #head
        kHead = (k - 0) / (kLimit- 0)
        xStart = pntUpLimit.X()
        xEnd = pntDaoStart.X()
        dx = (xEnd-xStart)*(1 - kHead)
        pnt0 = getPntTranslate(pntFocus, dx, 0, 0)
        pnt1 = getPntTranslate(pntLimit, dx, 0, 0)
    else: #tail    
        kTail = (k - kLimit) / (1 - kLimit)
        angle = -angleEnd*kTail
        pnt0 = pntFocus
        pnt1 = getPntRotate(pntFocus, pntLimit, angle)
    return pnt0, pnt1


def getWireDaoSec(shapeDao, pntFocus, k):
    
    pntsDao = getPntsOfShape(shapeDao)
    pntDownLimit, pntDaoStart, pntUpLimit, pntDaoEnd = pntsDao
    
    p1, p2 = getPntsForDaoSec(pntDaoStart, pntUpLimit, pntDaoEnd, pntDownLimit, 
                              pntFocus, k)
    sectionPlane = getFacePlane(p1, p2, 3)
    
    pnt0, pnt1 =  getPntsEdgesFacesIntersect(shapeDao, sectionPlane)
    pntUp = getPntSectionUp(pnt0, pnt1)
    circle = GC_MakeCircle(pnt0, pntUp, pnt1).Value()
    edge = BRepBuilderAPI_MakeEdge(circle).Edge()
    wire =  BRepBuilderAPI_MakeWire(edge).Wire()
    return wire

   
def slide_03_DaoSecPrincipe(r, offset, k, h):
    
    drawCircle(r + offset,  'stInfo')
    pntsBase = getPntsBase(r)
    wireDaoClassic = getWireDaoClassic(pntsBase)
    wireDao0 = getShapeOffset(wireDaoClassic, -offset)
    ScShape(wireDao0, 'stMain')
    
    # for oure goal we need divide Dao on Head and Tail
    # Head sections is parallell
    # Tail sections is focused on focus point
    pntsDao0 = getPntsOfShape(wireDao0)
    pntDownLimit, pntDaoStart, pntUpLimit, pntDaoEnd  = pntsDao0
    
    # we need focus to determine tail sections 
    pntFocus = getPntDaoFocus(r)
    ScPoint(pntFocus, 'stMain')
    ScLabel(pntFocus, 'F' ,'stMain')
    
    # we need two points to determine section
    pnt1, pnt2 = getPntsForDaoSec(pntDaoStart, pntUpLimit, pntDaoEnd, 
                                  pntDownLimit, pntFocus, k)
    ScLine(pnt1, pnt2, 'stFocus')
    
    # !!! we need use plane to detect intercsect (not line) becouse 3D
    planeSec = getFacePlane(pnt1, pnt2, h)
    ScShape(planeSec, 'stFocus')

    pntsSec =  getPntsEdgesFacesIntersect(wireDao0, planeSec)
    drawPoints(pntsSec, 'stFocus')
    
    wireSec = getWireDaoSec(wireDao0, pntFocus, k)
    ScShape(wireSec, 'stFocus')

Ссылка на WebGL-презентацию: Слайд 03 Принцип построения сечений

Здесь понадобилась еще одна нетривиальная операция - пересечение кривой и поверхности. В качестве кривой выступает построенный нами двухмерный дао-контур. В качестве поверхности выступает вспомогательная плоскость, она проходит из фокуса под углом, определяемым нашим k. Алгоритм пересечения работает надежно и устойчиво. При первых попытках мне показалось, что он выдает ошибку. Но в результате оказалось что ошибался я, а алгоритм отрабатывает на пятерочку.

Хотелось бы еще немного порассуждать вот на какую тему? Почему мы ищем пересечение кривой и плоскости - не проще ли найти пересечение прямой и кривой? Ответ в том, что не проще. Не забывайте, что мы в 3D а здесь пересечение двух кривых необычное и редкое событие. Данный алгоритм попросту не существует.

Можно конечно вернуться в 2D, но это сложный путь. Из 2D в 3D перейти просто, а обратно гораздо сложнее. Поэтому думаю, что выйдя однажды в 3D лучше оставаться там до конца карьеры :) Хорошая новость заключается в том что практически для любой проблемы существуют изящные 3D решения.

Раз уж была затронута эта тема, хочу немного сказать о 3D-мышлении. Мне очень нравится все что касается объемного конструирования, это затрагивает какие-то базовые нейронные структуры, возможно где-то в глубине, на уровне мозжечка и я от всего этого испытываю реальный кайф. Откуда это у меня - я думаю все дело в близких мне людях.

Хочется рассказать про отца. Это боевой конструктор старой закалки. И я до сих пор учусь у него использовать инженерный подход к различным проблемам, начиная от философских и заканчивая бытовыми.

Еще хочется рассказать о моих институтских друзьях. Когда я учился в институте в нашем небольшом провинциальном городке, мне повезло и я, так сказать, попал в 3D-обойму. Это была группа студентов, которых посылали от кафедры графики по всей России на различные соревнования по начертательной геометрии, черчению, конструированию, и прочим вещам. Замечу, что это были лихие девяностые и перед руководителями кафедры часто стоял прямой выбор - выплатить зарплату, купить принтер, или послать группу студентов на соревнования. К чести кафедры выбор почти всегда делался в пользу соревнований. Так вот в этой 3D-обойме были действительно уникальные личности (похоже, что я там был самый бестолковый).

Расскажу один эпизод (а таких эпизодов был вовсе не один). Мой хороший друг Сергей (а он тоже был в обойме), в смутные времена, когда все сидели без денег устроился на некую сомнительную работу. Работа заключалась в том, что где-то на окраине города в сыром и темном подвале стоял высокоточный современный американский металлообрабатывающий центр (я все это видел своими глазами). И Сергей вытачивал на нем на заказ детали весьма причудливой формы. Никакого специального ПО, кроме карандаша и бумаги у него не было. Все команды он вводил непосредственно с пульта станка. Однажды между делом он выточил некую деталь, основу которой составляла коническая многозаходная резьба весьма сложного профиля. Про это узнали. Среди научно-технической элиты города поползли нехорошие слухи, что где-то на задворках происходит какая-то технологическая чертовщина. Слухи достигли авиационного моторного завода и об этом узнал начальник одного из серьезных цехов. Этот начальник все выяснил и лично спустился в сырой и темный подвал, чтобы увидеть все эти чудеса. Потому что весь его отдел, вооруженный Юниграфиксами, очень часто не мог сделать то что нужно.

Надеюсь, я вас немного поразвлек и можно двигаться дальше по узкой китайской тропинке.

Итак, в результате работы алгоритма пересечения получаем две искомые точки, через которые просто проводим симметрично расположенную окружность. Сечение готово. Чтобы проверить, как это работает построим сечения для k от 0 до 1 c постоянным шагом.

def slide_04_DaoManySec(r, offset, kStart, kEnd, cnt):
    
    drawCircle(r + offset, 'stInfo')
    pntsBase = getPntsBase(r)
    wireDaoClassic = getWireDaoClassic(pntsBase)
    wireDao0 = getShapeOffset(wireDaoClassic, -offset)
    ScShape(wireDao0, 'stMain')
    
    pntsDao0 = getPntsOfShape(wireDao0)
    pntDownLimit, pntDaoStart, pntUpLimit, pntDaoEnd  = pntsDao0
    
    pntFocus = getPntDaoFocus(r)
    
    for i in range(cnt+1):
        k = i/cnt
        kkScale = kEnd - kStart
        kk = kStart + k* kkScale
        p0,p1 = getPntsForDaoSec(pntDaoStart, pntUpLimit, pntDaoEnd, 
        pntDownLimit, pntFocus, kk)
        ScLine(p0, p1, 'stFocus')
        wireSec = getWireDaoSec(wireDao0, pntFocus, kk)
        ScShape(wireSec, 'stMain')

Ссылка на WebGL-презентацию: Слайд 04 Форма Дао из сечений

Итак мы проникли в святая святых и выяснили форму бесформенного Дао. Что теперь делать с этим сакральным знанием? Как из всего этого получить нормальное тело?

Предлагаю воспользоваться методом, который называется протягиванием. Он заключается в том, что специальному алгоритму предъявляются последовательные сечения тела и он пытается построить поверхность. Все это относится к широкой области моделирования с ограничениями. Еще можно встретить термины скининг (натягивание кожи), пайпинг (делание трубы).

Должен отметить что главное при протягивании - не протянуть ноги, подбирая различные параметры различных алгоритмов. Посмотрим как поведет себя наше ядро.

Шаг 7. Получаем готовую геометрию

Первая мысль - задать как можно больше сечений и алгоритм разберется, что к чему. К сожалению так не получится. Процесс аппроксимации - сложная штука. И в принципе нужно стремится к тому, чтобы ограничений накладываемых на алгоритм было как можно меньше. Если кто-нибудь рисовал сплайны, то он знает, что наиболее красивые формы получаются, когда мы уменьшаем количество точек а не увеличиваем. Нужно выбрать минимальное количество сечений, которые сформируют максимально точную геометрию.

Чтобы процесс протягивания был конструктивным и приятным я сделал следующие вещи.

Создал в Python список, содержащий коэффициенты опорных сечений и вывел эти сечения их на экран.
Кроме того я вывел на экран сам контур Дао, который мы нарисовали на втором шаге. Как известно этот контур является Абсолютной Истиной. По отношению к этой истине мы и будем оценивать наши результаты.

Не буду утомлять описанием подбора количества и расположения сечений. Скажу лишь, что это не заняло много времени, потому что была организована хорошая обратная связь - сразу было видно где форма отклоняется от идеала. Представляю конечный результат усилий.

def slide_05_DaoSkinning (r, offset):
    
    drawCircle(r + offset,  'stInfo')
    pntsBase = getPntsBase(r)
    wireDaoClassic = getWireDaoClassic(pntsBase)
    wireDao0 = getShapeOffset(wireDaoClassic, -offset)
    ScShape(wireDao0, 'stMain')
    
    pntsDao0 = getPntsOfShape(wireDao0)
    pntDownLimit, pntDaoStart, pntUpLimit, pntDaoEnd  = pntsDao0
    
    pntFocus = getPntDaoFocus(r)
    drawPoints(pntFocus, 'stMain')
  
    ks = [ 3, 9 , 16, 24, 35, 50, 70, 85] 
    wiresSec = []
 
    for k in  ks:
       wireSec = getWireDaoSec(wireDao0, pntFocus, k/100)
       ScShape(wireSec, 'stMain')
       wiresSec += [wireSec]    
    
    solidDao0 = getShapeSkin(pntDaoStart, wiresSec, pntDaoEnd)
    ScShape(solidDao0, 'stFocus')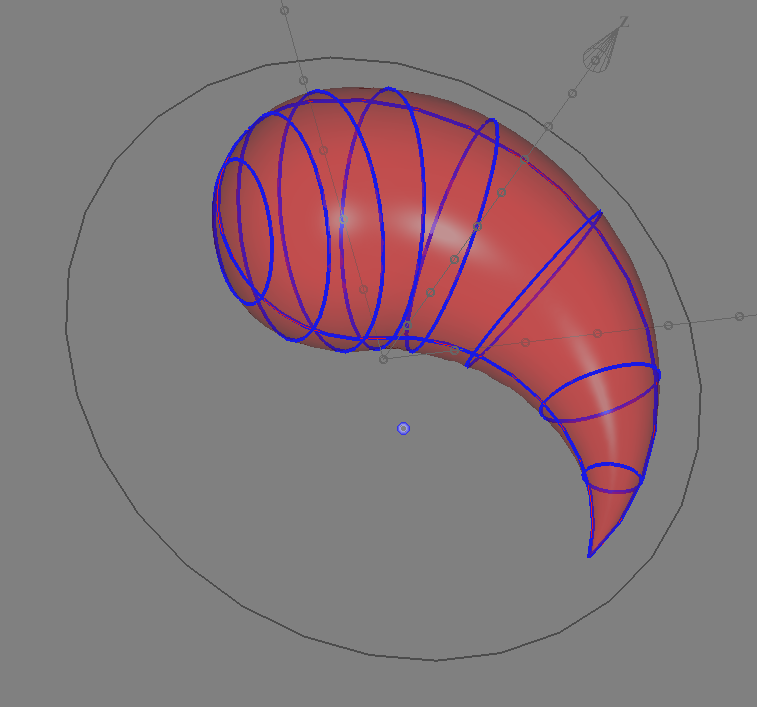

Рис 05 Протягивание поверхности через сечения

Ссылка на WebGL-презентацию: Слайд 05 Протягивание поверхности через сечения

Хочу обратить внимание на то, как получились начальная и конечные точки геометрии. Алгоритм понял, что начало должно быть гладким, а кончик острым. Честно говоря, я на это не надеялся и предвидел большие проблемы. Но все как-то получилось само собой. Давайте придадим нашей форме законченность. Во первых для придания динамизма и необычности - слегка приплюснем ее по вертикали.

Хочется немного рассказать с какой неожиданной проблемой я столкнулся. Никак не ожидал забуксовать на таком ровном месте. За различные преобразования в OpenCascade отвечает объект gp_Trsf. До сих пор он вел себя прилично и удовлетворительно. Но когда я с помощью его попытался приплюснуть геометрию у меня ничего не получалось. Началось с того, что я не нашел метода изменения масштаба отдельно по осям. Затем я пытался вручную задавать коэффициенты трансформации. Ничего не получалось. Объект магическим способом сопротивлялся всем попыткам.

Истина оказалась проста. OpenCascade конструкторское ядро и оно не для дешевых эффектов Поэтому базовый объект трансформации не позволяет искажать геометрию. Он защищает объекты от нелогичных изменений. Для тех же кто хочет большего и понимает зачем он это делает существует другой объект gp_GTrsf. Вот с помощью его то у меня все и получилось.

Далее мы скопируем нашу форму с разворотом на 180 градусов... Ой, простите на pi ... Да, да... конечно наpi :) И раскрасим все это в приятные цвета.

def getSolidDao(r, offset):
    
    pntsBase = getPntsBase(r)
    wireDaoClassic = getWireDaoClassic(pntsBase)
    wireDao = getShapeOffset(wireDaoClassic, -offset)
    
    pntsDao = getPntsOfShape(wireDao)
    pntDownLimit, pntDaoStart, pntUpLimit, pntDaoEnd  = pntsDao
    
    pntFocus = getPntDaoFocus(r)
   
    ks = [ 3, 9 , 16, 24, 35, 50, 70, 85] 
    wiresSec = []
 
    for k in  ks:
       wireSec = getWireDaoSec(wireDao, pntFocus, k/100)
       wiresSec += [wireSec]    
    
    solidDao = getShapeSkin(pntDaoStart, wiresSec, pntDaoEnd)
    solidDao = getShapeZScale(solidDao, 0.7)
    return solidDao
   
def slide_06_DaoComplete (r, offset):
    
    solidDao0 = getSolidDao(r, offset)
    ScShape(solidDao0, stDao0)
    solidDao1  = getShapeOZRotate(solidDao0, pi)
    ScShape(solidDao1, stDao1)

Ссылка на WebGL-презентацию: Слайд 06 Окончательная форма Дао

Шаг 8. Современная основа для древней философии

Согласитесь, даже гениальные идеи не могут висеть в воздухе, поэтому сделаем небольшую подставку для нашего объемного Дао. А заодно и проверим наше геометрическое ядро на прочность в плане булевых операций с объектами.

Вычесть куб из сферы - и так нелегкая задача. А когда в булевых операциях участвует геометрия, сформированная нетривиальным образом - результат не может предсказать никто. Вот и посмотрим на что действительно способен Open Source.

Код следующего шага несложный, чего не скажешь о стоящей за ним математике. Замечу, что для того, чтобы наши Инь и Янь удобно лежали на подставке я ввел параметр gap - технологический зазор по всему контуру - где-то 1 мм.

def getDaoCase(r, offset, h):
    r2 = r*2                                    
    h2 = h/2
    rTop = r + offset
    rSphere = gp_Vec(0,rTop,h2).Magnitude()
    sphere = BRepPrimAPI_MakeSphere(rSphere).Shape()
    limit = BRepPrimAPI_MakeBox( gp_Pnt(-r2, -r2, -h2), gp_Pnt(r2, r2, h2) ).Shape()
    case = BRepAlgoAPI_Common(sphere, limit).Shape()
    case = getShapeTranslate(case, 0,0,-h2)
 
    
    solidDao0 = getSolidDao(r, offset)
    solidDao1  = getShapeOZRotate(solidDao0, pi)
   
    case = BRepAlgoAPI_Cut(case, solidDao0).Shape()
    case = BRepAlgoAPI_Cut(case, solidDao1).Shape()
  
    return case
    
def slide_07_DaoWithCase (r, offset, caseH, caseZMove ,gap):
    
    solidDao0 = getSolidDao(r, offset+gap)
    ScShape(solidDao0, stDao0)
    solidDao1  = getShapeOZRotate(solidDao0, pi)
    ScShape(solidDao1, stDao1)
    
    case = getDaoCase(r, offset, caseH)
    
    case = getShapeTranslate(case, 0,0, caseZMove)
    ScShape(case, stCase)

Ссылка на WebGL-презентацию: Слайд 07 Форма Дао с основанием

Должен сказать, что получилось не сразу, но все-таки получилось. Да, обидно, что ядро спотыкается и мы вынуждены прибегать к шаманизму для получения результата. Но учитывая, какая сложная математика здесь присутствует можно сделать на это поправку.

Невидимое солнце Open Source

Вот и закончилось это увлекательное 3D-мистичекое-приключение. Боги к нам были благосклонны и практически все получилось. Оставляю несколько ссылок:

GitHub - Точка сборки - ссылка на репозиторий с проектом, в рамках которого было проделано это исследование.
makeDaoShape.py - ссылка на полный текст примера
Инь, Янь, Подставка. - ссылки на STL-файлы (мало ли кому пригодятся). Только пожалуйста - не перепутайте Инь и Янь - понятно что отличия минимальны, но кто знает этот загадочный Китай :)

Если подвести итог в целом, то мне понравилось знакомство с OpenCascade. Это просто чудо, что такие вещи лежат в открытом доступе и их можно изучать со всех сторон. Пусть порой было не все гладко. Да и код, который я написал совсем не совершенен. Но ведь идеального не бывает ничего. И это наверное самое интересное свойство нашего мира.

Нам надо знать, когда остановиться
Сосуд нельзя сверх меры наполнять
Большие ценности труднее охранять
И слишком острый меч быстрее притупится
Добром ли чином через чур гордится
Беду на дом свой накликать
Твой труд закончен, так умей уйти
Вот смысл силы, жизни и пути.

Великая книга Дао - Стих 9 ( Перевод Ю. Полежаевой)

OpenCASCADE и Невидимое солнце Дао